機械学習プロフェッショナルシリーズ「統計的因果探索」の勉強の続き。
前回の投稿でLiNGAMモデルがなぜ識別可能なのかについて触れました。
今回は実際にLiNGAMモデルの係数行列 $B$ をどうやって推定するかについて、Pythonのソースコードと合わせて見ていこうと思います。
※Pythonのソースコードは以下の本家(?)のサイトで紹介されているものを参考にしています。(ほぼそのまま写経してます)
https://sites.google.com/site/sshimizu06/lingam
大まかな推定の流れ
LiNGAMモデルの推定方法として
① 独立成分分析の手法を用いる
② 回帰分析と独立性評価を繰り返す
の2つがあり、上記サイトで紹介されているソースコードは①の独立成分分析の手法を用いるパターンなので、ここでも独立成分分析の手法を紹介しようと思います。
前回の投稿で触れたように、係数行列 $B$ は $B = I - D^{-1}P^{-1}W_{ICA}$ と表現できることをまず思い出します。
推定の流れは以下の通りです。(識別可能性の議論の流れと同様です。)
- 独立成分分析の推定法FastICAを用いて $W_{ICA}$ を推定(これを $\hat{W}_{ICA}$ と表記)
- $\hat{W}_{ICA}$ の対角成分の絶対値ができるだけ大きくなるように行を並び替える(置換行列 $P$ の推定。これを $\hat{P}$ と置く) $\Rightarrow$ 対角成分に $0$ が来ないように行を並び替える置換行列の推定と見なす
- $D$ を $\hat{D}=diag(\hat{P}\hat{W}_{ICA})$ と推定
ここまでで係数行列を $\hat{B} = I - \hat{D}^{-1}\hat{P}^{-1}\hat{W}_{ICA}$ と推定できるわけですが、推定の誤差により、綺麗に厳密な下三角行列になりません。それも踏まえて一旦Pythonによる実装を覗いて見ます。
サンプルデータとして以下の因果関係を持つデータを対象とします。
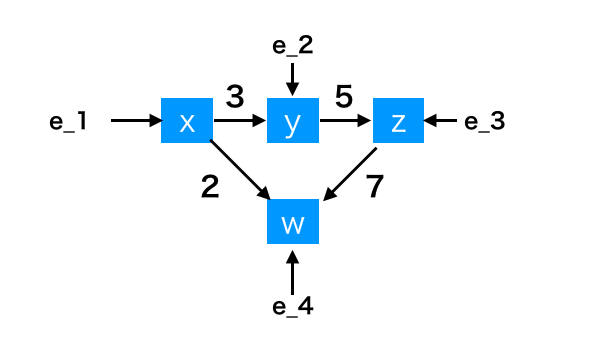
構造方程式で記述すると、
\begin{align}
x &= e_{1} \\
y &= 3x + e_{2} \\
z &= 5y + e_{3} \\
w &= 2x + 7z +e_{4}
\end{align}
であり、係数行列は以下になります。
B = \left (
\begin{matrix}
0 & 0 & 0 & 0\\
3 & 0 & 0 & 0\\
0 & 5 & 0 & 0\\
2 & 0 & 7 & 0\\
\end{matrix}
\right )
Pythonによる実装
まずは上記のサンプルデータを生成します。(外生変数は一様分布に従うとします。)
import numpy as np
size = 1000
np.random.seed(123)
x = np.random.uniform(size=size)
np.random.seed(456)
y = 3*x+ np.random.uniform(size=size)
np.random.seed(789)
z = 5*y+ np.random.uniform(size=size)
np.random.seed(135)
w = 2*x + 7*z+np.random.uniform(size=size)
xs = np.array([x,y,z,w]).T
# array([[6.96469186e-01, 2.33816347e+00, 1.20141522e+01, 8.61533324e+01],
# [2.86139335e-01, 1.02148479e+00, 5.33767105e+00, 3.82636707e+01],
# [2.26851454e-01, 1.46419762e+00, 8.11476695e+00, 5.74524697e+01],
# ...,
# [3.47146060e-01, 1.66909717e+00, 9.18710623e+00, 6.52045372e+01],
# [4.16848861e-03, 3.86523572e-01, 2.52848875e+00, 1.79734284e+01],
# [2.94894709e-01, 9.23529229e-01, 4.81468494e+00, 3.43320338e+01]])
FastICA
FastICAはsklearn.decompositionの中にあります。
mixing_ で独立成分分析の混合行列 $A$ を取得できます。
$A$ の逆行列が混合行列 $W$ でした。逆行列が必ずしも存在するとは限らないので、pinvで求めます。
下記のW_icaが $\hat{W}_{ICA}$ に相当します。
from sklearn.decomposition import FastICA
n_samples, n_features = xs.shape
ica = FastICA(random_state=1234, max_iter=1000).fit(xs)
W_ica = np.linalg.pinv(ica.mixing_)
print(W_ica)
# [[ 7.54427732e-03 -5.58044720e-01 1.15814118e-01 -6.66677048e-04]
# [ 1.10236389e-01 2.63830057e-03 1.16463040e-02 -1.69856229e-03]
# [-2.22900867e-01 -1.06213195e-02 -7.51532878e-01 1.07695296e-01]
# [ 3.22723819e-01 -1.17694641e-01 -1.42444083e-03 4.66761062e-04]]
対角成分が大きくなるように並び替え
W_icaの対角成分の絶対値ができるだけ大きくなるように並び替える。
言い換えると、W_icaの成分を絶対値の逆数で置き換えたものの対角成分をできるだけ小さくするような置換行列を探せばよい。
W_ica_ = 1 / np.abs(W_ica) # もちろんこの前に成分が0でないことはチェックする
print(W_ica_)
# [[1.32550801e+02 1.79197108e+00 8.63452588e+00 1.49997664e+03]
# [9.07141471e+00 3.79031870e+02 8.58641502e+01 5.88733191e+02]
# [4.48629928e+00 9.41502609e+01 1.33061378e+00 9.28545664e+00]
# [3.09862471e+00 8.49656359e+00 7.02029863e+02 2.14242378e+03]]
上記の行列W_ica_の対角成分ができるだけ小さくなるように行を並び替えるにはどうしたらいいでしょうか。各行各列から成分を一つずつ取り出し、その合計値が最も小さい組み合わせを求めればよさそうです。これは前回紹介したハンガリアン法という割当問題で解くことができそうです。
from munkres import Munkres
m = Munkres()
ixs = np.vstack(m.compute(deepcopy(W_ica_)))
print(ixs)
# [[0 2]
# [1 0]
# [2 3]
# [3 1]]
上記で求めた成分が対角成分に来るように行列W_icaを並び替えます
(今回であれば1行目→3行目、2行目→1行目、3行目→4行目、4行目→2行目に並び替えれば良さそうです。)
ixs = ixs[np.argsort(ixs[:, 0]), :]
ixs_perm = ixs[:, 1] # ixs_perm = [2 0 3 1]
W_ica_perm = np.zeros_like(W_ica)
W_ica_perm[ixs_perm] = W_ica
print(W_ica_perm)
# [[ 1.10236389e-01 2.63830057e-03 1.16463040e-02 -1.69856229e-03]
# [ 3.22723819e-01 -1.17694641e-01 -1.42444083e-03 4.66761062e-04]
# [ 7.54427732e-03 -5.58044720e-01 1.15814118e-01 -6.66677048e-04]
# [-2.22900867e-01 -1.06213195e-02 -7.51532878e-01 1.07695296e-01]]
Dの推定
上記で求めた行列W_ica_permの対角成分だけ引っこ抜いてやればよいので
D = np.diag(W_ica_perm)[:, np.newaxis]
W_ica_perm_D = W_ica_perm / D
print(W_ica_perm_D)
# [[ 1.00000000e+00 2.39331186e-02 1.05648454e-01 -1.54083630e-02]
# [-2.74204345e+00 1.00000000e+00 1.21028521e-02 -3.96586504e-03]
# [ 6.51412578e-02 -4.81845158e+00 1.00000000e+00 -5.75644023e-03]
# [-2.06973634e+00 -9.86238015e-02 -6.97832595e+00 1.00000000e+00]]
よって、 $\hat{B}$ は、
b_est = np.eye(n_features) - W_ica_perm_D
print(b_est)
# [[ 0.00000000e+00 -2.39331186e-02 -1.05648454e-01 1.54083630e-02]
# [ 2.74204345e+00 0.00000000e+00 -1.21028521e-02 3.96586504e-03]
# [-6.51412578e-02 4.81845158e+00 0.00000000e+00 5.75644023e-03]
# [ 2.06973634e+00 9.86238015e-02 6.97832595e+00 0.00000000e+00]]
因果的順序と回帰分析による推定
上記で求めた $\hat{B}$ は厳密な下三角行列になっていないので、このままでは因果関係を特定できません。
一般的に元のモデルが有向非巡回モデルであれば、 $\hat{B}$ を厳密な下三角行列にするような置換行列が必ず存在すると言われています。(これを因果的順序と言います。)
この後の議論の流れとしては、以下の通りです。
- $\hat{B}$ が厳密な下三角行列になるように因果的順序を推定
- $\hat{B}$ の下三角の成分を回帰分析(Lasso回帰)で推定
因果的順序の推定
LiNGAMモデル $\boldsymbol{x} = B\boldsymbol{x} + \boldsymbol{e}$ の両辺に置換行列 $\ddot{P}$ を左からかけると、
\begin{align}
\ddot{P}\boldsymbol{x} &= \ddot{P}B\boldsymbol{x} + \ddot{P}\boldsymbol{e} \\
&= \ddot{P}B\ddot{P}^{T}\ddot{P}\boldsymbol{x} + \ddot{P}\boldsymbol{e} \\
&= (\ddot{P}B\ddot{P}^{T})\ddot{P}\boldsymbol{x} + \ddot{P}\boldsymbol{e}
\end{align}
となり、これは観測変数ベクトル $\ddot{P}\boldsymbol{x}$ によるLiNGAMモデルと見なすことができます。$\ddot{P}B\ddot{P}^{T}$ が厳密な下三角行列であれば $\ddot{P}$ を元のLiNGAMモデルの因果的順序と見なすことができます。
上で推定した $\hat{B}$ に対して、 $\ddot{P}\hat{B}\ddot{P}^{T}$ が厳密な下三角行列に近くなるように $\ddot{P}$ を探します。どれだけ下三角行列に近いかどうかは、 対角成分と上三角成分の2乗和 $\sum_{i\leq j}(\ddot{P}\hat{B}\ddot{P}^T)^{2}$ で計算しますが、観測変数が多くなればなるほど、このような置換行列を探すのは困難になります。そこで膨大な計算量を回避できると言われている以下の方法が提案されています。
- (1) $\hat{B}$ の成分の絶対値が小さい順に $n(n+1)/2$ 個を $0$ と置き換える
- (2) 行を並び替えて下三角行列にできるか調べる。できなければ次に絶対値が小さい成分を $0$ と置いて再び確認
上記のステップはPythonで以下のように記述できます。
def _slttestperm(b_i):
# b_iの行を並び替えて下三角行列にできるかどうかチェック
n = b_i.shape[0]
remnodes = np.arange(n)
b_rem = deepcopy(b_i)
p = list()
for i in range(n):
# 成分が全て0である行番号のリスト
ixs = np.where(np.sum(np.abs(b_rem), axis=1) < 1e-12)[0]
if len(ixs) == 0:
return None
else:
ix = ixs[0]
p.append(remnodes[ix])
# 成分が全て0である行を削除
remnodes = np.hstack((remnodes[:ix], remnodes[(ix + 1):]))
ixs = np.hstack((np.arange(ix), np.arange(ix + 1, len(b_rem))))
b_rem = b_rem[ixs, :]
b_rem = b_rem[:, ixs]
return np.array(p)
b = b_est
n = b.shape[0]
assert(b.shape == (n, n))
ixs = np.argsort(np.abs(b).ravel())
for i in range(int(n * (n + 1) / 2) - 1, (n * n) - 1):
b_i = deepcopy(b)
b_i.ravel()[ixs[:i]] = 0
ixs_perm = _slttestperm(b_i)
if ixs_perm is not None:
b_opt = deepcopy(b)
b_opt = b_opt[ixs_perm, :]
b_opt = b_opt[:, ixs_perm]
break
b_csl = np.tril(b_opt, -1)
b_csl[ixs_perm, :] = deepcopy(b_csl)
b_csl[:, ixs_perm] = deepcopy(b_csl)
print(b_csl)
# [[ 0. 0. 0. 0. ]
# [ 2.74204345 0. 0. 0. ]
# [-0.06514126 4.81845158 0. 0. ]
# [ 2.06973634 0.0986238 6.97832595 0. ]]
今回は因果的順序がたまたま元の順序と一緒なので、厳密な下三角行列になります。
Lasso回帰による推定
残りは係数行列の下三角成分の推定になります。上記の議論で以下の因果関係が推定できます。
- $x$ はどの変数とも因果関係なし
- $x \rightarrow y$ という因果関係がありそう
- $x, y \rightarrow z$ という因果関係がありそう
- $x,y,z \rightarrow w$ という因果関係がありそう
でも実際は $x \rightarrow z$ という因果関係と $y \rightarrow w$ という因果関係はありません。ここまでの推定ではまだこのような冗長な因果関係が残ってしまっています。
そこで、Lasso回帰と呼ばれるスパース回帰※の一種を用いて、この冗長な因果関係を削除します。
(普通の線形回帰だと推定値がぴったり $0$ にならないので、冗長な因果関係を特定することができません。)
※スパースとは「疎」という意味でスカスカなイメージです。重要でないパラメータを削ぎ落とす際に使われる推定方法です。
参考:http://www.sigmath.es.osaka-u.ac.jp/shimo-lab/ja/research-new/sparse-estimation/
from sklearn import linear_model
model = linear_model.Lasso(alpha=0.01)
model.fit(y=y.reshape(size,-1), X=x.reshape(size,-1))
print("x->y", model.coef_)
model.fit(y=np.array([z]).T, X=np.array([x,y]).T)
print("x,y->z", model.coef_)
model.fit(y=np.array([w]).T, X=np.array([x,y,z]).T)
print("x,y,z->w", model.coef_)
# x->y [2.84725564]
# x,y->z [0. 4.99377086]
# x,y,z->w [1.03341435 0. 7.06054349]
冗長な因果関係が正しく $0$ と推定でき、これでようやく係数行列は
B = \left (
\begin{matrix}
0 & 0 & 0 & 0\\
2.84725564 & 0 & 0 & 0\\
0 & 4.99377086 & 0 & 0\\
1.03341435 & 0 & 7.06054349 & 0\\
\end{matrix}
\right )
と推定することができました。
因果の強さもほとんど綺麗に推定できているイメージですが、 $x \rightarrow w$ の因果の強さの精度がイマイチです...
Lasso回帰は冗長な因果関係を削ぎ落とすためだけに使って、因果の強さの精度は上で推定した値を用いたほうがいいのかな?