割当問題とは?
割当問題という問題をご存知でしょうか?
$n$ 人に $n$ 個の仕事を割り当てるとき、最も効率の良い割り当て方は何かを考える問題を「割当問題」といいます。
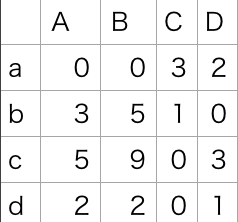
行列で考えるとわかりやすいです。下記の行列の行が人、列が仕事を表し、各成分は各人がそれぞれの仕事を終えるのにかかるコストととらえます。

各仕事に人は1人しか割り当てることができない状態で、全ての仕事に人を割り当てるとき、一番低コストな組み合わせを考えます。
このような問題を考える上で有名なアルゴリズムに「ハンガリアン法」(ハンガリー法)というものがあります。
ハンガリアン法
step1
各行の各要素からその行の最小値を引き、その後さらに各列の各要素からその列の最小値を引く。
step2
$0$ を各行各列から1つずつ選ぶことができるかどうか判定する。もし選ぶことができれば、その $0$ の座標の組みが割当案となる。選ぶことができなれければstep3へ。
step3
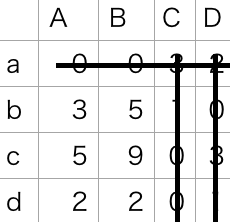
全ての $0$ をできるだけ少ない数の縦または横の線で覆う。
step4
線で消されていない要素から、それらの最小値を引き、縦横の線が交わる要素にその値を加える。step2に戻る。
上の表を実際にハンガリアン法の各stepを適用すると以下のようになります。
step2
$0$ を各行各列から1つずつ選ぶことができないのでstep3へ
step2
各行各列から $0$ を1つずつ選ぶことができる。選び方は以下の2通り(どちらも総コストは17)
[$(1,1), (2,4), (3,3), (4,2)$]
[$(1,2), (2,4), (3,3), (4,1)$]
上記の手順の注意として、
・step1は先に列から引いてもよい(その場合、次のstep2で割当案がいきなり求まる)
・step3でb行に線を引くと次のstep4でも各行各列から $0$ を選ぶことができないので、もう一度step3をする必要がある
などと、やり方によってすぐ求まったり、求められなかったりします。
pythonによる実装
本当にこのハンガリアン法で見つかる割当案が常に最適解なのかどうかの数学的証明は置いといて、今回はこのアルゴリズムをpythonで実装してみました。
(リスト内包表記の便利さを改めて実感しました)
import numpy as np
class Hungarian:
def __init__(self):
self.optimal = []
# step1
def _step1(self, mat):
output_mat = np.zeros_like(mat)
for i, row in enumerate(mat):
output_mat[i] = row - np.min(row)
return output_mat
# step2
def _step2(self, mat):
zero_coordinate = []
for i, row in enumerate(mat):
zero_coordinate.extend([(i, j) for j, v in enumerate(row) if v == 0])
check_row = []
check_column = []
for elem in zero_coordinate:
if not elem[0] in check_row and not elem[1] in check_column:
check_row.append(elem[0])
check_column.append(elem[1])
if len(check_row) != mat.shape[0]:
return False, zero_coordinate
return True, zero_coordinate
# step3
def _step3(self, mat, zero_coordinate):
zero_list = zero_coordinate
zero_count = {}
line = []
while(len(zero_list) > 0):
for elem in zero_list:
r = "r_" + str(elem[0])
c = "c_" + str(elem[1])
if r in zero_count: zero_count[r] += 1
else: zero_count[r] = 1
if c in zero_count: zero_count[c] += 1
else: zero_count[c] = 1
max_zero = max(zero_count.items(), key=lambda x:x[1])[0]
line.append(max_zero)
rc = max_zero.split("_")[0]
num = max_zero.split("_")[1]
if rc == 'r': zero_list = [v for v in zero_list if str(v[0]) != num]
else: zero_list = [v for v in zero_list if str(v[1]) != num]
zero_count = {}
return line
# step4
def _step4(self, mat, line):
output_mat = np.zeros_like(mat)
line_r = []
line_c = []
for l in line:
rc = l.split("_")[0]
num = int(l.split("_")[1])
if rc == 'r': line_r.append(num)
else: line_c.append(num)
line_cut_mat = np.delete(np.delete(mat, line_r, 0), line_c,1)
mini = np.min(line_cut_mat)
cross_point = [(i,j) for i in line_r for j in line_c]
non_line_point = [(i,j) for i in range(0,mat.shape[0]) for j in range(0,mat.shape[0]) if i not in line_r if j not in line_c]
for co in cross_point:
mat[co] += mini
for co in non_line_point:
mat[co] -= mini
return mat
def compute(self, mat):
mat = self._step1(mat)
mat = self._step1(mat.T).T
while(True):
flag, zero_coordinate = self._step2(mat)
if flag: break
line = self._step3(mat, zero_coordinate)
mat = self._step4(mat, line)
r = []
c = []
for v in zero_coordinate:
if v[0] not in r and v[1] not in c:
self.optimal.append(v)
r.append(v[0])
c.append(v[1])
return self.optimal
上記の行列に対して適用してみます。
# 行列を宣言
a = [5,4,7,6]
b = [6,7,3,2]
c = [8,11,2,5]
d = [9,8,6,7]
mat = np.array([a,b,c,d])
h = Hungarian()
h.compute(mat)
# output
# [(0, 0), (1, 3), (2, 2), (3, 1)]
割当案の座標が出力されました。うまくいっているようです。
もちろん、いちいち自分で実装なんかしなくても割当問題を解く便利なライブラリ「munkres」というものがあります。
pipでインストールできます。
pip install munkres
実際に使ってみます。
from munkres import Munkres
m = Munkres()
m.compute(mat)
# output
# [(0, 0), (1, 3), (2, 2), (3, 1)]
一撃でした。
参考
(pdfファイルがダウンロードされます)
http://www.ocw.titech.ac.jp/index.php?module=General&action=DownLoad&file=201115519-59655-0-28.pdf&type=cal&JWC=201115519