はじめに
去年、パチンコ屋で一番当たる台を見つける方法について研究したら、スペインのカナリア諸島で開かれた学会で発表できたのでその内容を宣伝します!

(写真は学会会場のホテル)
元論文は
Liyuan Xu, Junya Honda, and Masashi Sugiyama. "A fully adaptive algorithm for pure exploration in linear bandits." Proceedings of the 21st International Conference on Artificial Intelligence and Statistics (AISTATS2018). 2018.
[PDF]
ざっくり何をしたの?
「線形バンディット」における「最適腕識別問題」を解くアルゴリズムを提案し、提案手法は実データにおけるシミュレーションで既存手法と比べ約5倍の性能を見せました。ここでは「線形バンディット」と「最適腕識別問題」について説明します。
最適腕識別問題
「パチンコで一番当たる台を見つける問題」は数学的には最適腕識別問題として知られています。バンディット問題では「腕」と呼ばれる$K$台のスロットマシンとそれをプレイするagentが登場します。(スロットマシンといいパチンコといい、みんなギャンブル大好きすぎでしょ)
agentは$K$台のスロットマシン(腕)をいろいろプレイしてできるだけたくさん稼げるマシンを見つけようとします。この時に、できるだけ少ないプレイ回数で最適腕(もっとも期待報酬の高いマシン)を見つけ出すのが最適腕識別問題です。
最適腕識別問題の応用例
この問題は、スロットマシンのようなくだらない非現実的なものにしか応用できない、というわけではありません。最も有名な応用例はA/Bテストの最適化でしょう。
今機械学習での推薦アルゴリズムが3つあったとします。この中で最も売上につながる推薦アルゴリズムを選びたい時、通常のA/Bテストならユーザーを完全にランダムに分け、それぞれの性能を測るということをします。しかし、もし3つの中に明らかに悪い推薦アルゴリズムがあるなら、それに割り振られたユーザーの経験はとても悪いものになってしまいます。一方、最適腕識別アルゴリズムでは、各推薦アルゴリズムをスロットマシンとみなすことで、一旦悪いとわかった推薦アルゴリズムを二度と使用しないということが可能なため、A/Bテストによる売上の低下をとても小さく抑えることが出来ます。
線形バンディット
パチンコはスロットマシンと違って、台に事前情報(パチンコの機種・ピンの配置のタイプ etc)がついています。 先のA/Bテストの例だと、各アルゴリズムについての情報などが事前情報に当たるでしょう。このような事前情報を使ってより少ない回数で最も期待報酬の高い腕をみつける事が可能です。特に線形バンディットでは、以下が成り立つような事前知識をを仮定します。
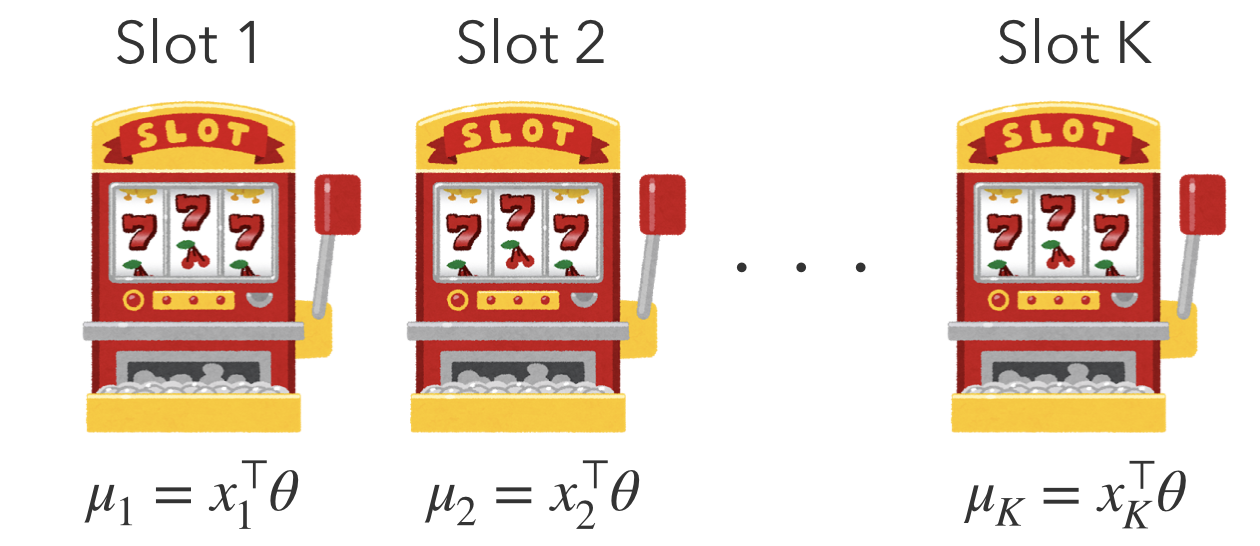
いま、各腕に特徴量$x_i$があり、それが観測可能であるとします。この時、$i$番目のマシンの期待報酬$\mu_i$がその特徴量の線形関数
$$\large \mu_i = x_i^\top \theta$$
で書けていることを仮定します。ただし、$\theta$は未知で、得られた報酬から推定しなくてはいけません。このような線形バンディットにおいて最適腕識別問題を考えるのがこの論文のテーマで、提案手法LinGapEが既存手法よりも遥かに少ないプレイ回数で最適腕を見つけられることを示しました。
既存研究との違い
論文が出た当時の既存研究は
Soare, Marta, Alessandro Lazaric, and Rémi Munos. "Best-arm identification in linear bandits." Advances in Neural Information Processing Systems. 2014. [PDF]
です。この論文との大きな違いは次にプレイする腕の選び方でした。既存研究では将来にプレイする腕をすべて事前に決めていたのに対し、提案手法は過去の情報から、次に引く腕を適応的に決めるというのが大きな改良点です。

こうすることによって最適腕を必要最低限のプレイ回数で見つけることが出来ます。
うまくいったよ!
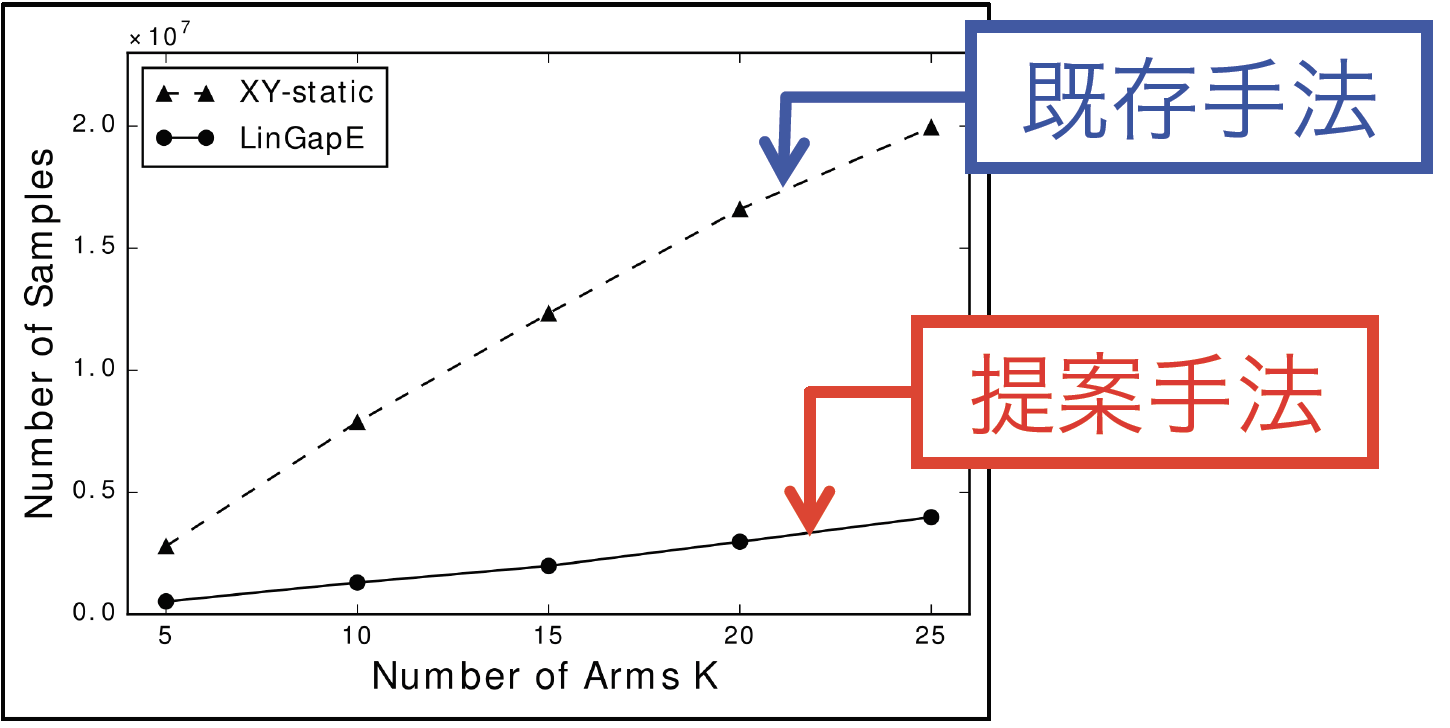
Yahoo! Webscope Dataset R6Aを元にした設定でシミュレーションを行った結果が下図です。(実験の詳細は論文を参照。)縦軸が最も良いスロットを見つけるまでにかかったプレイ数、横軸がスロットマシンの数です。これを見ると、提案手法が既存手法の1/5程度で最も良いマシンを見つけられているということがわかります。
もっとくわしく!
ここでは、上のざっくりした説明では物足りない人のためにちゃんと数式を使って論文の貢献と、具体的なアルゴリズムを説明します。
詳細な問題設定
今、$K$個のスロットマシンがあり、それぞれの特徴量を$x_1,\dots,x_K \in \mathbb{R}^d$と書くことにします。ここからは、バンディットの慣習に従い、各マシンのことを腕と呼ぶことにします。ここで、各腕の特徴量の集合を$\mathcal{X} = \{x_1,\dots,x_K\}$と書くことにし、特徴量の$l_2$ノルムの最大値を$L$とします。各時刻$t$において、agentは$K$個の腕中から一つ選び、報酬を観測します。いま、時刻$t$で選ばれた腕を$a_t \in \{1,\dots,K\}$としたとき、報酬$r_t$は
$$\large r_t = x_{a_t}^\top\theta + \varepsilon_t$$
によって生成されるとします。ここで、$\theta \in \mathbb{R}^d$は未知パラメータであり、$\varepsilon_t$は期待値ゼロ、分散$R^2$のノイズです。この分散$R$と未知パラメータ$\theta$の$l_2$ノルム$S$は既知であるとします。
この論文では**$(\varepsilon,\delta)$-最適腕識別を考えています。いま、期待報酬最大の腕(最適腕)を$a^*=\arg\max_i x_i^\top\theta $としたとき、 $(\varepsilon,\delta)$-最適腕識別は出力されたマシン $\hat{a}^*$が最適腕よりも$\varepsilon$以上悪い確率が$\delta$以下**であることを要求します。数式で書くと、以下のとおりです。
$$\large \mathbb{P}[(x_{a^*}-x_{\hat{a}^*})^\top\theta \geq \varepsilon] \leq \delta$$
この問題の目標はこのような$\hat{a}^*$をできるだけ少ないサンプル数で出力することです。
アルゴリズムの概要
線形バンディットの最適腕識別問題では、未知パラメータ$\theta$を推定しながら、次にプレイするマシンを決めていきます。このとき、以下のような少し面白い現象が起こります。
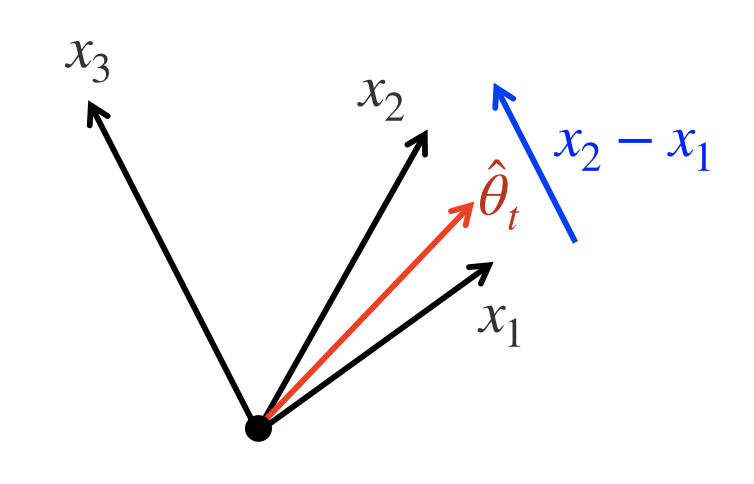
上の図において、$x_1,x_2,x_3$が2次元の特徴量で、上図のようなベクトルで表されるとしましょう。ここで、$\hat{\theta}_t$を$t$回プレイ後の$\theta$の推定とします。この時、推定期待報酬が高いのは腕1と2です。($x_1^\top \hat{\theta}_t$と$x_2^\top \hat{\theta}_t$が大きいため)。しかし、この2つのうちどちらが大きいか判定するためには腕3をプレイすべきです。なぜなら、腕1と2の期待報酬の差は
$$\large \theta^\top x_3 \propto \theta^\top (x_1 - x_2)$$
により、腕3をプレイすることで推定可能なためです。
上の事実により、提案手法は以下の三段階により、時刻$t$でプレイする腕$a_t$を決めます。
-
時刻$t-1$までの情報を用いて$\hat{\theta}_{t-1}$を求める。
-
$\hat{\theta}_{t-1}$を用いて、最適なマシンの候補を2つ(上の例だと腕1と2)を求める。
-
候補を見分けるのに有用な腕(上の例だと腕3)をプレイ。
アルゴリズムの詳細
ここでは提案アルゴリズムLinGapEの詳細を述べます。一応実験コードはGithubに存在するのですが、研究用にあわてて書いたコードなので、まちがっても人様に読ませるものにはなっていないです、すみません![]()
なので自分で実装したほうが早いかもです。(要望があれば整備します)
LinGapEの擬似コードは以下のとおりです。

(元論文より引用)
上の擬似コードにおいてはいくつかの行で具体的な計算が省略されているのでその補足をしていきます。
4行目と11行目の"update"
4行目と11行目では"update $A_t$ and $b_t$"とありますが、これは以下のような計算式で更新されます。
$$\large A_{t+1} \leftarrow A_t + x_tx_t^\top \quad b_{t+1} \leftarrow b_t + x_tr_t$$
こうすることにより、推定量$\hat{\theta}_t = A^{-1}_tb_t$が正則化パラメータ$\lambda$でのリッジ回帰(参考)となります。
6行目のSelect-direction
このSelection-directionは、下のような擬似コードで定義される関数です。
(元論文より引用)
ここで、
$$ \large
\begin{align*}
\beta_t(i,j) &= \|x_i-x_j \|_{A_t^{-1}}\left(R\sqrt{2\log\frac{\mathrm{det}(A_{t})^{\frac12}\mathrm{det}(\lambda I)^{-\frac12}}{\delta}} + \lambda^{\frac12}S\right)\
\hat{\Delta}_t(i,j) &= (x_i-x_j)^\top\hat{\theta}^\lambda_t
\end{align*}
$$
として論文中に定義されています。ここの部分は最適腕の候補として$i_t$と$j_t$を選び出しており、概要の2番「$\hat{\theta}_{t-1}$を用いて、最適なマシンの候補を2つを求める。」に相当する部分です。
9行目の"pull arm"
ここでいう pull arm $a_{t+1}$ とは、腕$a_{t+1}$をプレイする、ということだと思ってください。この部分では最適腕の候補$i_t$と$j_t$を元に次にプレイする腕を決める概要の3番「候補を見分けるのに有用な腕をプレイ」に相当する部分です。
論文中では、2通りの決め方を紹介しましたが、どちらも大して性能に差がなかったので、実装の楽な

とすることをおすすめします。
理論解析
論文では提案手法が確率$1-\delta$で最適腕より$\varepsilon$以上悪い腕を出力しないということを示しています。さらに、このときに必要なサンプル数$\tau$についても、
$$ \large
\tau\leq 8H_\varepsilon R^2\log\frac{K^2}{\delta} + C
$$
であることを示しています。(上の具体的な定義は論文参照。)理論的な貢献としてこれが既存手法よりも遥かに小さいことも示しています。