OLS (最小2乗回帰)
出典:https://scikit-learn.org/stable/modules/linear_model.html#ordinaly-least-squares
一見この式で十分に思えるが、実際は何でもありの関数ができてしまう
リッジ回帰
出典:https://scikit-learn.org/stable/modules/linear_model.html#ridge-regression
重みが大きくなることも損失とみなす
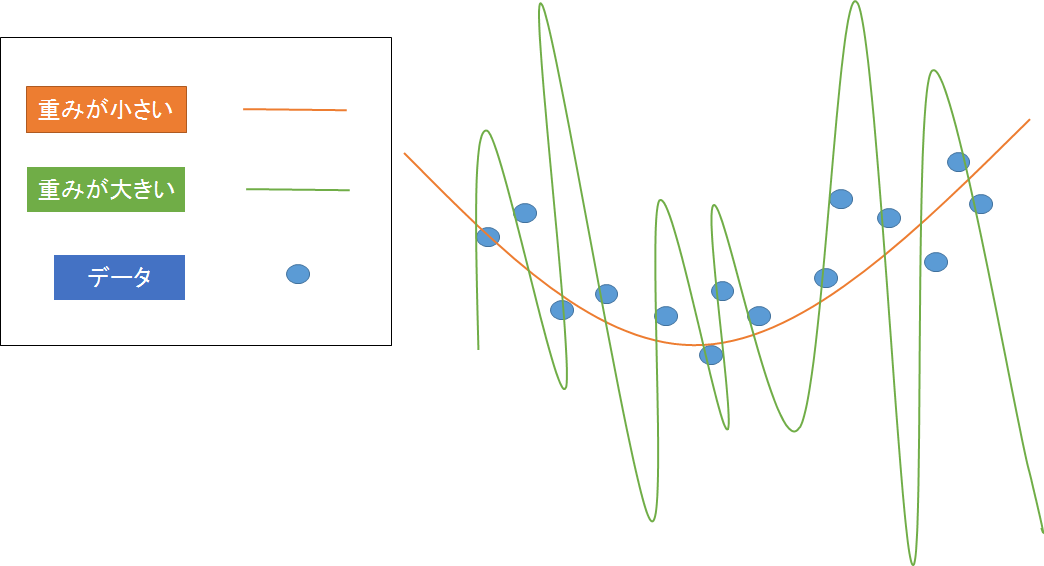
イメージ
重みの大きさを抑えることをしないとどういった関数になるかのイメージ
・重みが小さいと大まかな傾向を捉えた関数になる
・重みが大きいとすべてのデータを通るような関数になる
正則化の効果
<OLS>
・誤差さえ小さくなればどんな関数になってもいい
<Ridge>
・誤差を小さくしつつ、各重みも小さくする
・誤差を小さくするには重みを大きくしないといけない状況になったら、誤差を残してでも重みを小さいままにする(トータルで小さくする)
*重みが大きくなると関数は複雑化して過学習する
まとめ
リッジ回帰の式は過学習を防ぎながら誤差を小さくするという
機械学習において求められていることを端的に表している