自動着色
大分キャッチーなタイトルにしましたがただの解説と実験結果のような記事です。
Abstruct
近年Deeplearning界隈をにぎわせたものとしてpix2pixという技術があります。*1
これはGANという技術の応用として開発され、画像から画像へ変換させるニューラルネットとして例えば線画から猫を描いたりといった一風変わった技術として世間を賑わせてきました。
今回はその技術の解説とその応用としてアニメ画像の自動着色に私も挑戦してみます。
Generative Adversarial Network
はじめに
GANについて「DiscriminatorとGeneratorとのいたちごっこ」などといった比喩的表現は抑え、できるだけ詳細に私の理解の範囲で説明しました。今のところGANについては日本語で詳細に数式を追えてる記事はほぼないはずなので少しでも業界の一助となれば幸いです。どこかで間違えていると思うのでコメントで訂正していただけたら幸いです(決死の覚悟)。またより詳細に知りたい部分もコメントいただけたら幸いです。
あらかじめGANなどの概要は知っていることを前提とします。
DCGAN
通常のGANではGeneratorとDiscriminatorは以下の二つのloss関数を最大化および最小化させることで目的のNNを求めるのでした。$p_{data}$をデータセットの確率分布、$p_g$をGeneratorによって生成された確率分布としたとき、
\nabla_{\theta_d}\dfrac {1} {m} {\sum}^m_{i=1} \Bigl[ log\ D( x^i ) + log(1-D(G(z^i)) \Bigl]. \hspace{15pt} (1)
\nabla_{\theta_g}\dfrac {1} {m} {\sum}^m_{i=1} log\Bigl(1-D(G(z^i)\Bigl) \hspace{15pt} (2)
ではなぜこの二つのloss関数を最適化させることで目的のNNを手に入れられるのでしょうか。
GANの最終的な目的は「元のデータセットの確率分布と生成された画像の確率分布を近似させること」と表現できます。
Discriminatorのloss関数はGeneratorを固定し解析的に表すと(1)を考えると以下のようになります。
V(G,D) = \int_x p_{data}(x)log(D(x))dx + \int _{z} p_{z}(z)log\Bigl(1 - D(G(z)\Bigl)dz \hspace{15pt}
\int_x p_{data}(x)log(D(x)) + p_g(x)log\Bigl(1 - D(G(x)\Bigl)dx \hspace{15pt} (3)
また、一般的に a,bを0を除いた任意の実数としxを閉区間[0,1]の任意の実数とするとき
(a, b)\in\mathbb{R}\setminus\{0,0\}\hspace{15pt}
f(x)\rightarrow a\ log(x) + b\ log(1-x)
の最大値は微分すると\
$$ \dfrac { a} {a +b } \hspace{15pt} (4) $$
であることがわかります。したがって(4)式の(3)を応用させると
Discriminatorの解は潜在的な二つの確率分布を用いて以下の式で表現できることがわかります。
D^*_G(x) = \dfrac {p_{data}(x) } { p_{data}(x) + p_{g}(x) }\hspace{15pt} (5)
となります。
つまり(1)のloss関数は最適化し続けた場合暗黙的に(5)の式に近づいているということです。
それではこの解を$V(G,D)$に当てはめ$G$を変数としてもう一度式を再考してみましょう。
V(G,D)をDを最大のものとしてあてはめると
C(G) = {max}_D V(G, D) \hspace{15pt}
= \mathbb{E}_{x{\sim}p_{data}}[logD^*_G(x)] + E_{x {\sim}p_{data}}[log(1-D^*_G(x))]\hspace{15pt}
= \mathbb{E}_{x{\sim}p_{data}}\Bigl[log \dfrac {p_{data}(x)} { p_{data}(x) + p_{g}(x) }\Bigl] + E_{x{\sim}p_{data}}\Bigl[log \dfrac {p_{g}(x)} { p_{data}(x) + p_{g}(x) }\Bigl]\hspace{15pt} (6)
。
このとき$p_g = p_{data} $とすると $ D(x) = 1/2$であるので、(6)の最小値は$-log4$になると考えられます。
これはKLダイバージェンス距離を用いて表すと以下のようになります。
C(G(x)) =
-log(4) + KL\Bigl(p_{data} \mid\mid \dfrac {p_{data} + p_g} {2}\Bigl) + KL\Bigl(p_{g} \mid\mid \dfrac {p_{data} + p_g} {2}\Bigl)
さらにこれは Jensen–Shannonダイバージェンス距離を用いて表現すると
C(G) = - log(4)+ 2*JSD(p_{data} \mid\mid p_g)\hspace{15pt} (7)
Dを最適化し(5)式にしたあと、(1)を微分した(2)を最小化することは(7)を最小化させることに等しくなるということです。(7)でgを更新させると(5)をもう一度求めなければ行けないのでDとGを交互に更新していく必要があります。そうしていくことで最終的に互いが収束していくということです。(この辺の説明がもう少し詳しく論文に書いてあります。)
以上のによりGANの最適化問題は生成された画像とデータセットの集合の確率分布を近似させることは
式のloss関数の最適化問題に等しいことがわかりました。
Wasserstein GAN
しかしGANには実験していく中で様々な問題点が出ました。*15
理論上は(5)式を考えるとGを固定したときDの値は少なくとも$log4$以上に収束するはずですが、実際は0になってしまうというエラーがあげられます。
このエラーが発生する理由は二つあります。私の理解が正しければ一つ目は任意のドメイン画像が用意したニューラル多様体上で不連続であること、二つ目は二つの確率分布が全く交わりのない台を含んでしまう時です。数学においての台とは0にならないf(x)の値の集合のことです。
二つ目はわかりづらいので簡単な図で説明すると、
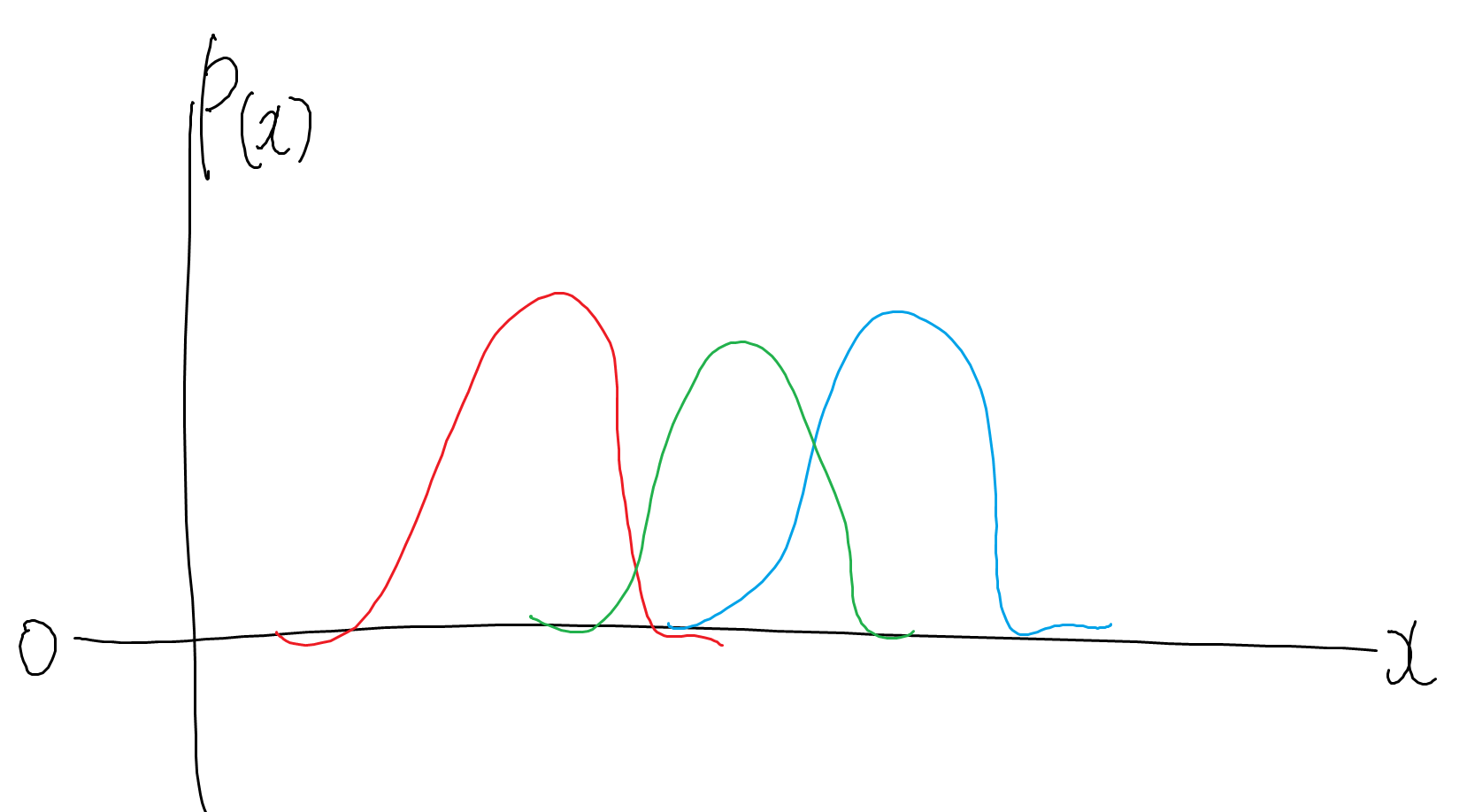
図0 青と赤ではエラーになる
この辺りの詳細な理由は*15の論文Towards Principled Methods for Training Generative Adversarial Networksに譲るとします・・・後のWGANもこの論文の著者である数学者二人がかかわっています。
それではこの距離関数に別の収束に安定性がある距離関数は適応できないのでしょうか?
WassersteinGANに関しては日本語でわかりやすく解説された記事は*12あたりです。
距離関数にはさまざまなものがありますが、その一種のにWasserstein距離というものがあります。
非常に単純な式に見えますが、Wasserstein距離に用いることができる確率分布は以下の式により制限されています。
\int _{M}d\left( x,x_{0}\right) d\mu \left( x\right) < +\infty\hspace{15pt} (8)
簡単にいうと、確率分布でもどっかの値で無限に発散することはない確率分布だと思っていただければ結構です。
そしてこのような確率分布の距離関数は以下のように表現することができます。これがいわゆるWasserstein距離です。
Generatorの出力分布を$\mathbb{P}{\theta} $ データ分布を $\mathbb{P}_{r}$ とすると以下の式で表現できます。
W(p_r, p_{\theta}) = {\inf}_{{\gamma}\in{\pi}}\int_x\int_y \mid\mid x- y \mid\mid {\gamma}(x,y)dxdy \hspace{15pt} (9)
この式から(8)の制限をなくし一度${\gamma}\in{\pi}$とたときの項を加え以下のように表現してみます。
W(p_r,p_{\theta}) = \inf_{\gamma} \mathbb{E}_{ x,y\sim {\gamma} }[\mid\mid x-y\mid\mid + \underbrace{\sup_f \mathbb{E}_{s\sim r}[f(s)]- \mathbb{E}_{t\sim p_{\theta} }[f(t)]-(f(x)-f(y))}_{= \begin{equation}
\left \{
\begin{array}{l}
0 \ \ {if} \ \ γ \in {\pi}\\
+{\infty} {else}
\end{array}
\right.
\end{equation}\hspace{15pt} (10)} ]
= \inf_{\gamma}\ \sup_f \mathbb{E}_{ x,y\sim {\gamma} }[\mid\mid x-y\mid\mid + \mathbb{E}_{s\sim r}[f(s)]- \mathbb{E}_{t\sim p_{\theta} }[f(t)]-(f(x)-f(y))]
(10)の部分は少しわかりずらいかもしれませんが、期待値の中で考えていて、$γ\in {\pi}$ではどこがサンプリングされても発散された値は取られないため$f(x)$は$E[f(x)]$と同じで合計すると0になることがイメージできるはずです。(多分)
ここで$f(x)$はリプシッツ写像であることを条件としています。
リプシッツ写像とは以下の式で定義されるものを言います。*13
距離空間$(X,d_X), (Y,d_Y)$の間の写像$f$に対し、正の定数λで任意の$x,x'{\in}X$に対して
d_Y(f(x),f(x')) < {\lambda}d_X(x,x') ({\forall}x, {\forall}x' \in X)\hspace{15pt} (11)
をみたすものが存在するとき$f$はλリプシッツであるといおう。また$λ$をリプシッツ定数といいます。
この記事では$λ=1$の場合のみ考え対応するリプシッツ写像は1-Lipschitzと表現します。
また参考文献11によるとinfとsupは入れ替えられるらしいので、
式を整理すると以下のようになります。
W(p_r,p_{\theta}) = \sup_f\ \inf_{\gamma} \mathbb{E}_{ x,y\sim {\gamma} }[\mid\mid x-y\mid\mid + \mathbb{E}_{s\sim r}[f(s)]- \mathbb{E}_{t\sim p_{\theta} }[f(t)]-(f(x)-f(y))]. \hspace{15pt} (12)
これをもう一度整理すると
W(p_r,p_{\theta}) = \sup_f \mathbb{E}_{s\sim p_r}[f(s)]- \mathbb{E}_{t\sim p_{\theta} }[f(t)] + \underbrace{\inf_{\gamma}\mathbb{E}_{ x,y\sim {\gamma} }[{\mid\mid x-y\mid\mid -(f(x)-f(y))}}_{= \begin{equation}
\left \{
\begin{array}{l}
0 \ \ {if} \ \ \mid\mid f\mid\mid_L \leq 1\\
-{\infty} {else}
\end{array}
\right.
\end{equation}\hspace{15pt} (13)} ]. \
そこで$f(x)$を1-Lipschitzとすると(13)は0になります。それ以外の場合は$-{\infty}$に発散します。
したがって$f(x)$が1-Lipschitzであることを仮定すると
W(p_r,p_{\theta}) = \sup_{\mid\mid f\mid\mid_L \leq 1} \mathbb{E}_{s\sim p_r}[f(s)]- \mathbb{E}_{t\sim p_{\theta} }[f(t)] . \hspace{15pt} (14)
以上によりwasserstein距離を用いた二つの確率分布の距離の測り方がわかりました。
距離を小さくするためにGeneratorで微分すると(14)式は
\nabla_{\theta}W(p_r,p_{\theta}) = -\mathbb{E}_{s\sim p_r}[f(t)]
=-\dfrac {1}{M}\sum_{m=1}^M[f(g(z^{(m)}))] \hspace{15pt} (15)
となります。
(14)で正確な距離を求め(15)でその距離を最小化せるという方法で求まるはずです。
異常がざっくりとしたWasserstein 距離を用いたGANの解説でした。
リプシッツ写像を機械的に表現するためににはかつてはweightをクリッピングするという方法が一般的でした。
しかしそのようなWGANではweightが例えばclip(-0.01, 0.01)にすると-0.01と0.01に偏ってしまうという現象が起きてしまいます。図1を参照ください (*6 引用 )
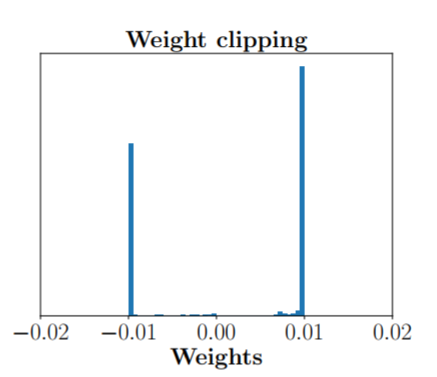
図1クリッピングによりweightが分散した様子
ではより表現力が高いネットワークでリプシッツ写像を満たすWeightを作り出すにはどうしたらいいのか?ということから考え出された技術がImproved WAsserstein GANというものです。
Discriminatorの更新式に風変わりな項を加えています。
L =\mathbb{E}_{\widetilde{x}\sim\mathbb{P}_{r}}[D(\widetilde{x})] - \mathbb{E}_{x\sim\mathbb{P}_{\theta }}[D(x)] + \lambda \mathbb{E}_{\hat{x}\sim\mathbb{P}_{x}} [(\left\| \nabla_{\hat{x}}D(\hat{x}) \right\|^{2} - 1)^{2}]. \hspace{15pt} (16)
ここで${\hat{x}}$とはデータセットのサンプルを$\widetilde{x} \sim P_r$ とし潜在変数$z \sim p(z) $とし $ε \sim U[0,1]$としたとき
\hat{x} =ε\widetilde{x} + (1-ε)x\hspace{15pt} (17)
でサンプルされた変数です。U[0,1]は0から1までの一様ランダムな変数。
論文の最後の方に書いてあることを簡単に説明すると私の理解が正しければ$f(x)$が1-Lipthsizであることを仮定すると
以上の分布からとれる値を$x$としたときの$f(x)$の勾配のL2ノルムは1であることが証明されています。
それを応用し、loss関数の項にその値から1を引いて二乗すればweight decayのようにペナルティーとして加算されるため、そのうち$f(x)$はリプシッツ写像になるはずだという考えです。
実際、以上によるloss関数の操作でweightの分散が以下のようになります。
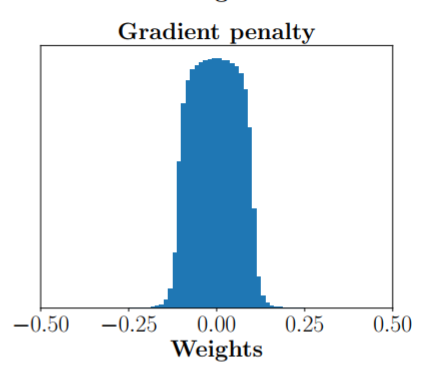
図2 Gradient penaltyによりweightが上手く分散した様子
実際にスコアを見てみても通常のWGAN以上に精度は高いようです!
Self-Normalizing Neural Networks (SELU)
活性化関数には様々なものがありますが、今回紹介するのはSELUというその関数のうちの一つです。
結果からあげるとかなり単純な数式で表現できます。
selu(x) = λ \begin{equation}
\left \{
\begin{array}{l}
x \ \ if \ \ \ x > 0 \\
αe^x-α \ \ \ if \ \ \ x < 0
\end{array}
\hspace{15pt} (18)
\right.
\end{equation} \\
λ \approx 1.0507 \\
α \approx 1.6733
あまり理解していないので中途半端に解説します。
この $λ$ および $α$ の値は以下の式から導かれております。LaTexがつかれたんでスクショにします・・・
$p_N$を正規分布とし$μ$および$ν$をニューラルネットの現在の層の一つ前の層の出力の平均と分散とし$ω$および$τ$を一つ前の層のweightの平均と分散としたとき、現在の層のインプットの平均と分散は以下の式で計算することができます。
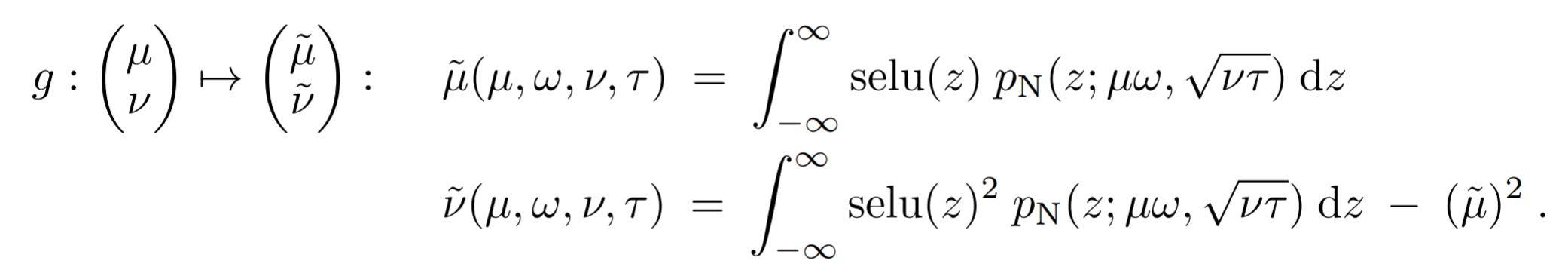
式(19)
これはニューラルネットの各層のニューロンへのインプットは(19)で使っているようなガウス分布で近似することができることを仮定することで成り立つ式です。論文Figure14参照。
また、これを代数的に解くと
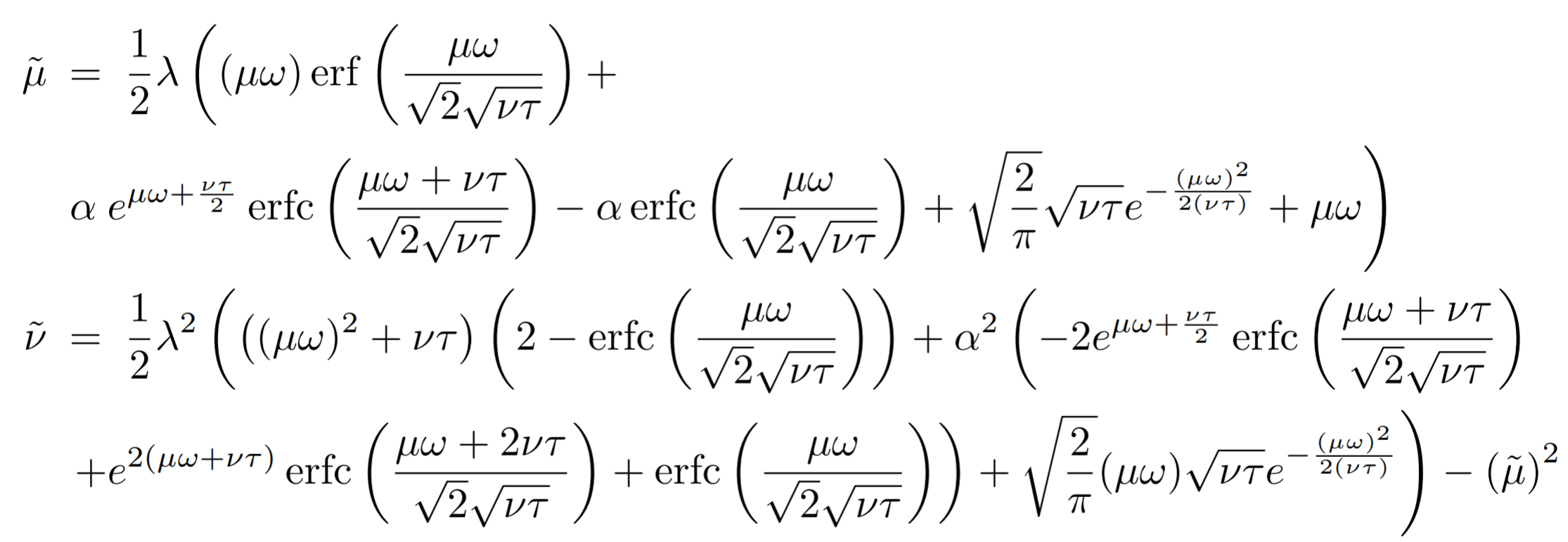
式(20)
となるらしいです。$\tilde{μ}$および$\tilde{ν}$に0および1を代入し、$α$および$λ$の値を導出してるはずです。この式から察するに私の理解が正しければ、SELUを使用すと「ウェイトおよび一段階下の出力層の平均が0、分散が1の場合、出力の平均が0、分散が1である」ということを保証しています。
(20)から最終的な$λ$および$α$を導いています。
したがってこれを使用することでBatch Normalizationのように強制的に出力の分散を変更し、ネットワーク全体の表現力を高めるといった作業をする必要がなくなるということです。多分。なんでウェイトを更新しても上記のことが保証されてんでしょう?そのうち頑張って解説します(多分)
論文では102ページもかけていろいろ説明しています。。。ものすごい数式の分量なので今回は結果だけ使わせていただきます。
Hackers News でこの論文のサマリーがまとめられ少し議論されていましたがあまり大したは書いてありませんでした。*1
アニメ着色
今回は以上の技術をTensorflowと併用して実装しアニメ画像の自動着色をしてみました。
目新しいものがほしいと思ったためLoss関数やアクティベーション関数を少し工夫し以下の要素で試してみました。
・L1 Distance only
・L1 Distance + GAN
・improved Wasserstein GAN
・Self-Normalizing Neural Networks (SELU) as activation fucntion
L1 Distance + GANは大体ご存知の通りだと思われます。
データセットの作り方
基本的に入力データとして線画、教師データとして本来の画像を与えています。
線画の抽出に関しては*2を参考にしました。
データセットはDanbooruという海外のサイトをスクレイピングすることで集めて学習しています。
Result
結果です。あまり面白くありません。データセットの中にあった二つの画像で比較していきます。
左側を教師データ、右側を入力データとして学習し生成していきました。
どれも1万枚ぐらいの学習セットを半日ぐらい学習しています。
それでは結果を見ていきましょう。
入力データ
L1 Distance
実際はもっとセピア調に近かった気がしますのでもしかしたらこれはλ = 100.0の間違えかもしれません。
L1 Distance + GAN ( λ = 10.0 )
L1 Distance + GAN ( λ = 1.0 )
さらに色味がついてきました。
Improved wasserstein gan
SELU , SELU ( + WGAN )
どっちがどっちだか忘れましたが、収束しませんでした()
Conclusion
結論としてL1 Distance + GAN ( λ=1.0 )ぐらいが一番いい感じになるというつまらない結果になってしまいました。
目新しさと言ったらWasserstein GANをpix2pixのような少し複雑なネットワークに応用させても収束するということが分かったぐらいです。
GANにSELUを応用させるとうまくいくという結果は*16のリンクをたどってみたのですが、うまくいかないのは何か原因があるのでしょうか?収束結果としては通常のGANよりもいいスコアをたたき出していそうなためもう少し研究を進めてみる価値がありそうです。
実験用のコードは以下のGithubにあげております。ご参照ください。
また、今回は集めたデータセットの良し悪しを事前にチェックして省いていませんが、先に悪いものを省けばもう少しいい自動着色ができるかもしれません。
GitHub
https://github.com/latte0/paints_tf
( work in progress )
Future work
最近Appleがiosアプリ向けにCore MLという既存の機械学習フレームワークの学習済みモデルを組み込めるライブラリを提唱してました。
Tensorflow のモデルが移植できたかは忘れましたが何かしら自動着色もできるお絵かきアプリが開発できたら面白いと思うので開発します。
疲れました。
Reference
*1 Image-to-Image Translation with Conditional Adversarial Networks
https://arxiv.org/abs/1611.07004
*2 線画抽出
https://hogehuga.com/post-1642/
*3 Generative Adversarial Network
https://arxiv.org/abs/1406.2661
*4 Wasserstein GAN
https://arxiv.org/abs/1701.07875
*5 Improved WassersteinGAN
https://arxiv.org/abs/1704.00028
*6 Self-Normalizing Neural Networks
https://arxiv.org/abs/1706.02515
*8 ご注文は機械学習ですか?(Wasserstein GANについての解説 )
http://musyoku.github.io/2017/02/06/Wasserstein-GAN/
*9 Hackers New (SELUについてのまとめと議論 )
https://news.ycombinator.com/item?id=14527686
*10 線画抽出について
https://news.ycombinator.com/item?id=14527686
*11 Wasserstein 距離についての解説。海外の含めても一番わかりやすいような気がするので誰かにまるまる翻訳してほいしい。
https://vincentherrmann.github.io/blog/wasserstein/
*12 Read-through: Wasserstein GAN
http://www.alexirpan.com/2017/02/22/wasserstein-gan.html
*13 リプシッツ写像について(日本語)
http://surgery.matrix.jp/lectures/josai/gen_top/gt2004a.pdf
*14 [DL輪読会]Wasserstein GAN/Towards Principled Methods for Training Generative Adversarial Networks
DCGANの問題点からWassersteinGANにつなげるまでがうまかった
https://www.slideshare.net/DeepLearningJP2016/dlwasserstein-gantowards-principled-methods-for-training-generative-adversarial-networks
*15 Towards Principled Methods for Training Generative Adversarial Networks ( WGANが考案されるまでのGANの問題点と指摘 )
https://arxiv.org/abs/1701.04862
*16 Alexia Jolicoeur-Martineau(seluとDCGANの話)
https://ajolicoeur.wordpress.com/cats/










