LoginSignup
51
31

More than 3 years have passed since last update.

制御工学Advent Calendar 2019Day 12
@larking95

データ駆動型制御器設計法の紹介

Last updated at Posted at 2019-12-11

はじめに

フィードバック制御は家電から産業機器までさまざまなものを「制御」するために用いられてきました。
この制御を行うものを制御器と呼び，この設計法はいろいろ考えられてきました。
今回は，その中でも比較的新しい「データ駆動型制御器設計法」というアプローチについて紹介したいと思います。

なお，理論的な部分は論文に譲ることにして，利用することを中心に書こうと思います。
ですので，MATLABとPythonのコードを交えながら説明したいと思います。

データ駆動型制御に至るまで

制御器の設計にはざっくり言えば以下の3つのアプローチがあります。

  1. 手動でパラメータ調整（限界感度法など）
  2. モデルベース制御器設計（最適レギュレータなど）
  3. それ以外（$H_{\infty}$制御やデータ駆動型制御など）

1は手動ですから，試行錯誤していかなければならず，設計が大変なのは想像に難くありません。
そこで，2のように制御対象の数理モデルをきっちり求めて，モデルを使って設計する手法が提案されました。
このモデルをきっちり求めるという作業を「同定」と呼びます。
同定されたモデルを用いて最適化問題を記述することで，我々は理論的に最適な制御器を得ることができるようになりました。
しかし，このモデルをきっちり求めるというのが曲者で，理論と実験をすり合わせるにはなかなかに手間がかかります。
そこで，モデルはきっちり求まらないという前提に立つ，それ以外の手法が検討されました。
データ駆動型制御はその中の1つです。

データ駆動型制御とは？

電気通信大学の金子先生のHPによれば，データ駆動型制御とは

制御対象の機器の駆動時のデータやその振る舞いから、直接コントローラを設計する手法

です。
つまり，モデルを作成することなく，ただ駆動時の信号のデータさえあれば制御器が設計できるのです。

データ駆動型制御器設計法として現在有名な方法として以下の2つがあります1。

VRFT
(Virtual Reference Feedback Tuning)		 FRIT
(Fictious Reference Iterative Tuning)
提案者 M.C. Campi, S. Savaresi 金子修
論文掲載年 2002 (Automatica) 2004 (ISCIE)
注目するデータ 制御入力 $u(t)$ 制御出力 $y(t)$
最適化問題 線形(最小二乗法で解ける) 非線形(非線形ソルバーが必要)
ライブラリ提供 MATLAB toolbox あり MATLAB toolbox あり

今回は，最適化問題が簡単に解けるためVRFTについてコードを書いてみました。
（FRITについてはこちらの記事にまとめました。）

サンプルコードの実行環境

なお，説明中のPythonコードではインポート文などを省略しています。
動作するコードは 全体のコード を参照してください。

VRFTの手順

VRFTを利用するにあたって設計者が行うべきことは3つだけです。
1. 設計仕様の決定
2. 入出力データの取得
3. アルゴリズムに従って最適化問題を解く

今回は，モータを使った速度制御系の制御器設計を例にして説明していきます。

設計仕様の決定

まず，設計仕様を決定しましょう。
設計仕様としては以下の3つを決定できます。

仕様 説明
参照モデル $M(z)$ 実現したい閉ループ応答の伝達関数
周波数重み $W(z)$ 評価したくない周波数でゲインが下がる伝達関数
制御器の構造 $\boldsymbol{\beta}(z)$ 制御器の次数などを決める

例えば，時定数 $\tau = 0.02$ [s]の応答をPID制御器によって実現したい場合は，

\begin{align}
M(s) &= \frac{1}{0.02 s + 1} \\&= \frac{50}{s + 50}\\
\boldsymbol{\beta}(s) &= \begin{bmatrix}1& \frac{1}{s}& s\end{bmatrix}^\mathrm{T}
\end{align}

のように設定します。
また，高域ではデータにノイズが混在する可能性が高いことを考慮して，周波数重みにはローパスフィルタを設定しておけば十分なことが多いです。

以上をコードにすると以下のようになります。

vrft.m
% サンプリングタイムと演算子
Ts = 0.001;
s = tf('s');        % ラプラス演算子 s
z = tf('z', Ts);    % 時間進み演算子 z

% 参照モデル M
tau = 0.02;
M = c2d(1/(tau*s + 1), Ts); % ゼロ次ホールドで離散化した一次遅れ系

% 重み関数
gW = 100;
W = c2d(gW/(s + gW), Ts);   % ゼロ次ホールドで離散化した一次遅れ系

%制御器構造 beta
beta = minreal([1; Ts/(1 - z^-1); (1 - z^-1)/Ts]); % PID制御器
vrft.py
# === 設計仕様の決定 ===
# サンプリング時間
Ts = 0.001

# 参照モデル M
tau = 0.02
M = ctl.c2d(ctl.tf([1], [tau, 1]), Ts)  # ゼロ次ホールドで離散化した1次遅れ系

# 重み関数 W
gW = 100
W = ctl.c2d(ctl.tf([gW], [1, gW]), Ts)  # ゼロ次ホールドで離散化した1次遅れ系

# 制御器構造 beta
A, B, C, D = abcd_normalize(
    [[1., 0], [0, 0]],
    [[1.], [-1.]],
    [[0, 0], [Ts, 0], [0, -1/Ts]],
    [[1.], [0], [1/Ts]])
beta = ctl.ss(A, B, C, D, Ts)
del A, B, C, D

入出力データの取得

次に，制御対象から入出力データ${u_0(t), y_0(t)}$を取得します。
VRFTの場合は，以下の条件を満たすようにデータを取得します。

  • 必ず，開ループ（制御器なしの $P(s)$ のみ）の応答を取得する
  • 可能であれば，白色性の入力信号 $u_0(t)$ を用いる

白色性の信号としてはシステム同定で良く用いられるM系列信号を用いるとよいです。
M系列信号はMATLABの場合，System Identification Toolboxのidinput関数を用いて簡単に生成ができます。
Pythonの場合には，Scipyのmax_len_seq関数で生成ができます。
ただし，MATLABとは違う系列の信号が生成されるようですので，今回のPython版では関数prbs()を自作し利用しました。

ここで，シミュレーションを行うには制御対象（今回はモータ）のモデルが必要2になります。
なので，本来はモータのモデルの説明も必要かと思っていたのですが，Manao様の素晴らしい記事を見つけました。
ですので，ここではモデリングについては省略して，モータは一次系で表せるものとします。

よって，シミュレーションでは以下のようなコードでデータの取得が可能です。

vrft.m
%データ取得に用いる入力信号 u  (m系列信号)
n = 15;                                     % 段数
T = 2^n - 1;                                % 1周期当たりのデータ数
p = 15;                                     % データの周期数
N = T*p;                                    % データ数
u0 = idinput([T 1 p],'prbs',[0,1],[-1,1]);   % 信号のベクトル

% 入力信号のパワースペクトル密度 phi_u
phi_u = 1;                  %入力信号は白色性と仮定

% 制御対象モデル P
Tp = 0.74;
Kp = 1.02;
P = c2d(Kp/(Tp*s + 1), Ts);

% 出力信号 y0
y0 = lsim(P, u0);
vrft.py
# === 入出力データの取得 ===
def prbs(n, p):
    # matlab compatible PRBS signal generator

    taps = {3: [0, -1], 4: [0, -1], 5: [1, -1], 6: [0, -1], 7: [0, -1],
            8: [0, 1, 6, -1], 9: [3, -1], 10: [2, -1], 11: [8, -1],
            12: [5, 7, 10, -1], 13: [8, 9, 11, -1], 14: [3, 7, 12, -1],
            15: [13, -1], 16: [3, 12, 14, -1], 17: [13, -1], 18: [10, -1]}
    N = (2**n - 1)*p
    x = np.ones(n, dtype=np.int8)
    u = np.zeros(N, dtype=np.int8)
    tap = taps[n]
    for i in range(N):
        u[i] = x[-1]
        x0 = x[tap[0]] ^ x[tap[1]]
        x = np.roll(x, 1)
        x[0] = x0
    return u


# データ取得に用いる入力信号 u  (m系列信号)
n = 15
T = 2**n - 1
p = 15
N = T*p
# u0, _ = max_len_seq(n, length=N)  # MATLABとは違う系列の信号となってしまう
u0 = prbs(n, p)
u0 = -(2.*u0 - 1.)

# 入力信号のパワースペクトル密度 phi_u
phi_u = 1.

# 制御対象モデル P
Tp = 0.74
Kp = 1.02
P = ctl.c2d(ctl.tf([Kp], [Tp, 1]), Ts)

# 出力信号 y0
y0, t0, _ = ctl.lsim(P, u0)

アルゴリズムに従って最適化計算を解く

最後に，VRFTのアルゴリズムに従って信号を生成し，最適化計算を解きます。

VRFTが目指すのはできる限り参照モデル $M(z)$ に近い応答なので，これは評価関数 $J_\mathrm{MR}(\boldsymbol{\rho})$の最小化問題となります。

\begin{align}
J_\mathrm{MR}(\boldsymbol{\rho}) &= \left\| \left( \frac{P(z) C(z, \boldsymbol{\rho})}{1 + P(z) C(z, \boldsymbol{\rho})} - M(z) \right) W(z) \right\|_2 ^2
\end{align}

ここで，$\boldsymbol{\rho}$は制御器パラメータを表しており，$C(z, \boldsymbol{\rho}) = \boldsymbol{\rho}^{\rm T} \boldsymbol{\beta}(z)$ の関係にあります。
しかし，この式は制御対象のモデル $P(z)$ を使っているので，これを入出力データで書き換える必要があります。
理論的な説明はバッサリカットしますが，最終的に評価関数 $J_\mathrm{MR}$ を最小化する問題は 以下の$J_\mathrm{VR}^N$ を最小化する問題は漸近的に等価になります。

\begin{align}
J_{\rm VR}^{N}(\boldsymbol{\rho}) &= \frac{1}{N} \sum_{t=1}^{N}(u_L(k) - \boldsymbol{\rho}^{\rm T} \boldsymbol{\varphi}(t))^2
\end{align}

ここで，時系列データ $u_L(t)$ と $\boldsymbol{\rho}$は，フィルタ $L(z)$を用いて，以下の式で生成可能です。

\begin{align}
u_L(t) &= L(z) u_0(t)\\
y_L(t) &= L(z) y_0(t)\\
%\boldsymbol{\varphi}(k) &= \boldsymbol{\beta}(z) (\tilde{r}_L(t) - y_L(t))
e_L(t) &= (M^{-1} - 1)y_L(t)\\
\boldsymbol{\varphi}(k) &= \boldsymbol{\beta}(z) e_L(t)
\end{align}

ただし，フィルタ $L(z)$ は以下を満たすものとします。

\begin{align}
|L(z)|^2 &= \frac{|1-M(z)|^2 |M(z)|^2 |W(z)|^2}{\phi_u(\omega)} &\forall \omega
\end{align}

すると，$J_\mathrm{VR}^N(\boldsymbol{\rho})$ は制御対象のモデル $P(z)$を使うことなく，入出力データ${u_0(t), y_0(t)}$だけで記述可能です。
また，この式は制御器パラメータ $\boldsymbol{\rho}$に対して線形なので，最小二乗法で解くことが可能です。

以上より，最適化問題を解く部分は以下のようなコードになります。

vrft.m
% プレフィルタ L
L = minreal(M*(1 - M)/phi_u);

% フィルタに通した入力信号 ul
ul = lsim(L, u0);

% 疑似誤差信号 el
el = lsim(L*(M^(-1) - 1), y0);

%パラメータ前の制御器出力 phi
phi = lsim(beta, el);

%最適なパラメータ rho
rho = phi\ul;               % 行列形式で最小二乗法を解く(mldivide)

%設計した制御器 C
C = minreal(rho.' * beta);  % 制御器を求める

%評価関数 Jmr
Jmr = mean(ul - phi * rho); % 行列形式で評価関数を確認
vrft.py
# === VRFTによる設計 ===
# プレフィルタ L
L = ctl.minreal(M*(1 - M)/phi_u)

# フィルタに通した入力信号 ul
ul, _, _ = ctl.lsim(L, u0)

# 疑似誤差信号 el
el, _, _ = ctl.lsim(ctl.minreal(L*(M**-1 - 1)), y0.flatten())

# パラメータ前の制御器出力
phi, _, _ = ctl.lsim(beta, el.flatten())

# 最適なパラメータ rho
solution = np.linalg.lstsq(phi, ul, rcond=None)
rho = solution[0]

# 設計した制御器 C
C = ctl.ss([0], [0, 0, 0], [0], rho.T, Ts) * beta   # 制御器を求める

# 評価関数 Jmr
Jmr = np.mean(ul - np.dot(phi, rho))    # 行列形式で評価関数を確認

性能の確認

上記の手順で，制御対象のモデルを使うことなく入出力データのみを用いて制御器の設計ができたようです。
得られた最適な制御器パラメータ $\rho$ は以下の通りです。
MATLABとPythonでほぼ同等な結果が得られていることが分かります。

MATLAB Python 理論値3
比例ゲイン $K_p$ $35.4$ $35.4$ $36.3$
積分ゲイン $K_i$ $47.8$ $47.8$ $49.0$
微分ゲイン $K_d$ $0.00$ $-9.59 \times 10^{-16}$ $0.00$

では，本当にこの制御器で参照モデルの応答が実現できているか確認してみましょう。
確認するコードは以下の通りです。

vrft.m
% 制御器を実装したシステム全体 G
G = minreal(feedback(P*C, 1));

% ステップ応答
fig1 = figure('name', 'Step plot');
stepplot(G, M);
legend({'$$\frac{CP}{1+CP}$$', '$M$'},...
    'Interpreter', 'latex', 'FontSize', 14, 'Location', 'southeast');

%ボード線図表示
fig2 = figure('name', 'Bode plot of controller');
bodeplot(G, M, {1,100});
vrft.py
# === 性能の確認 ===
# 制御器を実装したシステム全体 G
G = ctl.minreal(ctl.feedback(P*C, 1))

# ステップ応答
plt.figure()
plt.title("Step response of closed loop system")
timeRange = np.arange(0, 0.12 + Ts, Ts)
ym, _ = ctl.step(M, timeRange)
yg, _ = ctl.step(G, timeRange)
plt.plot(timeRange, ym, timeRange, yg)
plt.xlabel("Time [s]", usetex=True)
plt.ylabel("Velocity [V]")
plt.legend(['Reference model', 'Closed loop system'], loc='lower right')

# ボード線図表示
plt.figure()
plt.title("Bode plot of closed loop system")
ctl.bode(M, G)
plt.legend(['Reference model', 'Closed loop system'], loc='lower left')
plt.show()

ここでは，ステップ応答だけ画像を載せておきます。
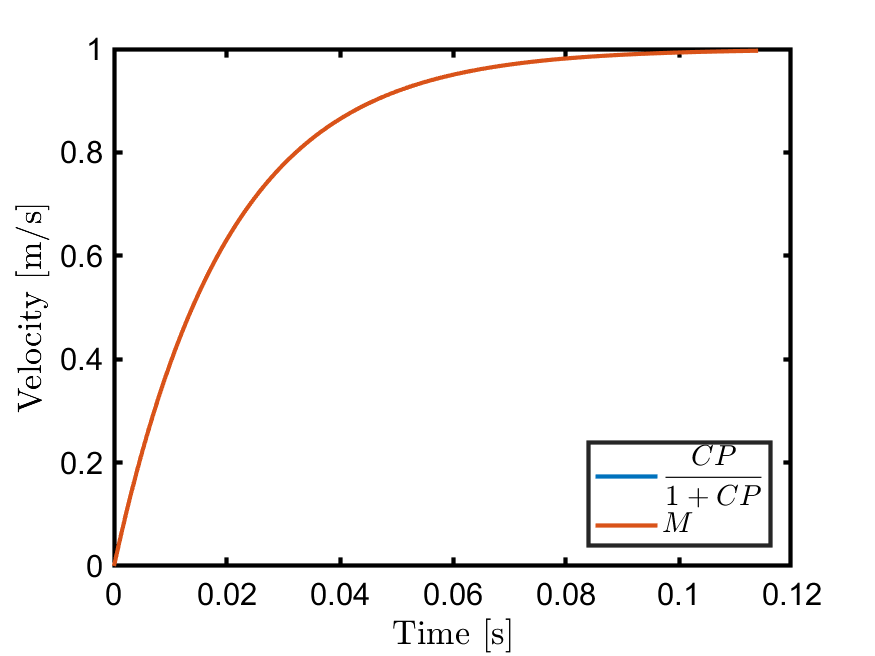
step.png
見分けがつかないくらいの精度で参照モデルの応答が再現できていることが分かります。

全体のコード

最後に，紹介してきたコードの全体を示します。

MATLAB を使った場合のコード vrft.m
vrft.m
% VRFTの設計スクリプト
% モータの速度制御系に対して設計する。

% Copyright (c) 2019 larking95(https://qiita.com/larking95)
% Released under the MIT Licence 
% https://opensource.org/licenses/mit-license.php

%% 初期化
clearvars;
close all;

%% 設計仕様の決定
% サンプリングタイムと演算子
Ts = 0.001;
s = tf('s');        % ラプラス演算子 s
z = tf('z', Ts);    % 時間進み演算子 z

% 参照モデル M
tau = 0.02;
M = c2d(1/(tau*s + 1), Ts); % ゼロ次ホールドで離散化した一次遅れ系

% 重み関数
gW = 100;
W = c2d(gW/(s + gW), Ts);   % ゼロ次ホールドで離散化した一次遅れ系

%制御器構造 beta
beta = minreal([1; Ts/(1 - z^-1); (1 - z^-1)/Ts]); % PID制御器

%% 入出力データの取得
%データ取得に用いる入力信号 u  (m系列信号)
n = 15;                                     % 段数
T = 2^n - 1;                                % 1周期当たりのデータ数
p = 15;                                     % データの周期数
N = T*p;                                    % データ数
u0 = idinput([T 1 p],'prbs',[0,1],[-1,1]);   % 信号のベクトル

% 入力信号のパワースペクトル密度 phi_u
phi_u = 1;                  %入力信号は白色性と仮定

% 制御対象モデル P
Tp = 0.74;
Kp = 1.02;
P = c2d(Kp/(Tp*s + 1), Ts);

% 出力信号 y0
y0 = lsim(P, u0);

%% VRFTによる設計
% プレフィルタ L
L = minreal(M*(1 - M)/phi_u);

% フィルタに通した入力信号 ul
ul = lsim(L, u0);

% 疑似誤差信号 el = 
el = lsim(L*(M^(-1) - 1), y0);

%パラメータ前の制御器出力 phi
phi = lsim(beta, el);

%最適なパラメータ rho
rho = phi\ul;               % 行列形式で最小二乗法を解く(mldivide)

%設計した制御器 C
C = minreal(rho.' * beta);  % 制御器を求める

%評価関数 Jmr
Jmr = mean(ul - phi * rho); % 行列形式で評価関数を確認

%% 性能の確認
% 制御器を実装したシステム全体 G
G = minreal(feedback(P*C, 1));

% ステップ応答
fig1 = figure('name', 'Step plot');
stepplot(G, M);

%ボード線図表示
fig2 = figure('name', 'Bode plot of controller');
bodeplot(G, M, {1,100});

Python Control を使った場合のコード vrft.py
vrft.py
# -*- coding: utf-8 -*-
"""
VRFTの設計スクリプト
モータの速度制御系に対して設計する。

Copyright (c) 2019 larking95(https://qiita.com/larking95)
Released under the MIT Licence 
https://opensource.org/licenses/mit-license.php
"""

import matplotlib.pyplot as plt
import numpy as np
import control.matlab as ctl

# from scipy.signal import max_len_seq
from scipy.signal import abcd_normalize


def prbs(n, p):
    # matlab compatible PRBS signal generator

    taps = {3: [0, -1], 4: [0, -1], 5: [1, -1], 6: [0, -1], 7: [0, -1],
            8: [0, 1, 6, -1], 9: [3, -1], 10: [2, -1], 11: [8, -1],
            12: [5, 7, 10, -1], 13: [8, 9, 11, -1], 14: [3, 7, 12, -1],
            15: [13, -1], 16: [3, 12, 14, -1], 17: [13, -1], 18: [10, -1]}
    N = (2**n - 1)*p
    x = np.ones(n, dtype=np.int8)
    u = np.zeros(N, dtype=np.int8)
    tap = taps[n]
    for i in range(N):
        u[i] = x[-1]
        x0 = x[tap[0]] ^ x[tap[1]]
        x = np.roll(x, 1)
        x[0] = x0
    return u


# === 設計仕様の決定 ===
# サンプリング時間
Ts = 0.001

# 参照モデル M
tau = 0.02
M = ctl.c2d(ctl.tf([1], [tau, 1]), Ts)  # ゼロ次ホールドで離散化した1次遅れ系

# 重み関数 W
gW = 100
W = ctl.c2d(ctl.tf([gW], [1, gW]), Ts)  # ゼロ次ホールドで離散化した1次遅れ系

# 制御器構造 beta
A, B, C, D = abcd_normalize(
    [[1., 0], [0, 0]],
    [[1.], [-1.]],
    [[0, 0], [Ts, 0], [0, -1/Ts]],
    [[1.], [0], [1/Ts]])
beta = ctl.ss(A, B, C, D, Ts)
del A, B, C, D

# === 入出力データの取得 ===
# データ取得に用いる入力信号 u  (m系列信号)
n = 15
T = 2**n - 1
p = 15
N = T*p
# u0, _ = max_len_seq(n, length=N)  # MATLABとは違う系列の信号となってしまう
u0 = prbs(n, p)
u0 = -(2.*u0 - 1.)

# 入力信号のパワースペクトル密度 phi_u
phi_u = 1.

# 制御対象モデル P
Tp = 0.74
Kp = 1.02
P = ctl.c2d(ctl.tf([Kp], [Tp, 1]), Ts)

# 出力信号 y0
y0, t0, _ = ctl.lsim(P, u0)

# === VRFTによる設計 ===
# プレフィルタ L
L = ctl.minreal(M*(1 - M)/phi_u)

# フィルタに通した入力信号 ul
ul, _, _ = ctl.lsim(L, u0)

# 疑似誤差信号 el
el, _, _ = ctl.lsim(ctl.minreal(L*(M**-1 - 1)), y0.flatten())

# パラメータ前の制御器出力
phi, _, _ = ctl.lsim(beta, el.flatten())

# 最適なパラメータ rho
solution = np.linalg.lstsq(phi, ul, rcond=None)
rho = solution[0]

# 設計した制御器 C
C = ctl.ss([0], [0, 0, 0], [0], rho.T, Ts) * beta   # 制御器を求める

# 評価関数 Jmr
Jmr = np.mean(ul - np.dot(phi, rho))    # 行列形式で評価関数を確認

# === 性能の確認 ===
# 制御器を実装したシステム全体 G
G = ctl.minreal(ctl.feedback(P*C, 1))

# ステップ応答
plt.figure()
plt.title("Step response of closed loop system")
timeRange = np.arange(0, 0.12 + Ts, Ts)
ym, _ = ctl.step(M, timeRange)
yg, _ = ctl.step(G, timeRange)
plt.plot(timeRange, ym, timeRange, yg)
plt.xlabel("Time [s]", usetex=True)
plt.ylabel("Velocity [V]")
plt.legend(['Reference model', 'Closed loop system'], loc='lower right')

# ボード線図表示
plt.figure()
plt.title("Bode plot of closed loop system")
ctl.bode(M, G)
plt.legend(['Reference model', 'Closed loop system'], loc='lower left')
plt.show()

おわりに

今回は理論はがっつり省略しつつ，データ駆動型制御器設計の概要とそのうちの1つのVRFTについて実際のコードについて紹介しました。
制御工学 Advent Calendar の他の参加者の皆様ほどの知識はありませんが，ご覧になった皆様がデータ駆動型制御に興味を持っていただける一助になれば幸いです。

また，気になる点などございましたら，お気軽にコメントいただければと思います。

追記

FRITについても記事を作成しましたので、興味のある方はそちらもご覧ください。(データ駆動型制御の紹介【2】)

参考文献

  1. VRFTの紹介 (Campi先生とSavaresi先生のサイト)
  2. FRITの紹介 (金子先生の紹介記事)
  3. システム同定の基礎 (足立先生の書籍)
  4. ArduinoとMATLAB/Simulinkを用いたDCモータのシステム同定 (Manao様の記事)
  5. NumPy for Matlab users (Scipy.org)

  1. 本当は歴史的に非反証制御やIFTとかも説明が必要でしょうが省略します。 ↩

  2. これはデータ取得に必要なだけで，設計には一切モデルは使わないことに注意してください。（実際，データ取得後 clearvars P としても設計は可能です。） ↩

  3. $M(z) = \frac{C^* (z) P(z)}{1 + C^* (z) P(z)}$ を満たす制御器 $C^*$の値（これを理想制御器と呼びます） ↩

51
31
4

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
51
31