LoginSignup
23
17

More than 3 years have passed since last update.

制御工学Advent Calendar 2020Day 12
@larking95

データ駆動型制御の紹介【2】

Last updated at Posted at 2020-12-12

Attention!!:warning:

この記事は，制御工学AdC2019で投稿したこちらの記事の続きです。
事前に前回記事をご覧いただくと，より読みやすいと思います。

はじめに

前回の記事では，データ駆動型制御器設計法の概要とVirtual Reference Feedback Tuning (VRFT) について説明しました。
今回はもう一つの有名な手法であるFictios Reference Iterative Tuning (FRIT)について，できる限りユーザーの立場に立ってコード中心に説明したいと思います。

前回のおさらい

データ駆動型制御は制御対象から得られたデータをそのまま使って直接制御器を設計する手法でした。
これによって，制御対象の数理モデルを作るためのシステム同定の手順をスキップすることができ，
設計する際の手間を減らすことができました。

例えば，前回紹介したVRFTでは，望みの閉ループ特性 $M(s)$ に非常に近い応答を時系列データのみから実現できました。
しかし，VRFTの場合，以下の２点が実用上の問題1 となります。

  1. M系列信号を印加する
  2. 開ループ実験が必要

M系列信号はいろんな周波数成分を等しく含むため設計には適した信号ではあるのですが，共振なども起こしてしまうため騒音や故障などの原因となる可能性があります2 。
また，開ループ実験が必要であるため，制御対象が不安定な場合にはデータ取得が困難です。
さらに，もし制御対象が安定だとしても，制御器の無い状態で機器を動作させることは故障などのリスクを伴います。

そこで，「現状でそれなりに動作している制御器」を「理論的に最適な制御器」に調整3 する方法が考えられました。
今回は，その代表的な手法であるFRITをコードを交えながら紹介します。

サンプルコードの動作確認環境

  • MATLAB 2020b
    • Control System Toolbox
    • Optimization Toolbox 4
  • Python 3.8.5 (非Anaconda環境)
    • matplotlib (v3.3.3)
    • numpy (v1.19.3)
    • scipy (v1.5.4)
    • python-control (v0.8.3)
  • TeX Live 2020 5

なお，説明中のPythonコードではインポート文などを省略しています。
動作する完全なコードは 私のgithub を参照してください。(MATLAB版 / Python版)

FRITの手順

FRITを利用するにあたって設計者が行うべきことは，次の3つだけです。

  1. 設計仕様の決定
  2. 入出力データの取得
  3. アルゴリズムに従って最適化問題を解く

今回も，モータを使った速度制御系の制御器設計を例にして説明していきます。
（制御対象と所望の設計仕様などの設定はVRFTの記事と全く同じとします。）

設計仕様の決定

まず，設計仕様を決定しましょう。
設計仕様としては以下の2つを決定できます。

仕様 説明
参照モデル $T_d(z)$ 実現したい閉ループ応答の伝達関数 6
周波数重み $W(z)$ 評価したくない周波数でゲインが下がる伝達関数
制御器の構造 $C({\boldsymbol\rho}, z)$ 制御器の分母と分子の次数などを決める

参照モデル$T_d(z)$と周波数重み $W(z)$は前回のVRFTと同じ意味です。
今回も，時定数$\tau=0.02$[s] の参照モデル $M(s)=50/(s+50)$，周波数重み $W(z)=100/(s+100)$ を与えます。

制御器の構造については，VRFTと少し異なります。
VRFTでは，制御器の分子パラメータの調整しか行えませんでしたが，
FRITでは，制御器の分子パラメータの調整も行うことができます。
つまり，次の式のような制御器のパラメータ$\rho_n$($l, m, n$は整数)を全て調整することができます。

\begin{align}
C({\boldsymbol\rho}, z) = \frac{
    \rho_1 z^l + \rho_2 z^{l-1} + \dots +\rho_l z + \rho_{l+1}
}{
    z^m + \rho_{l+2} z^{m-1} + \dots + \rho_{n-1}z +\rho_n
}
\end{align}

ただし，今回はPID制御器を調整したいので，サンプリング時間$T_s$を用いて，以下のように構造を与えました。

C({\boldsymbol\rho}, s) = \rho_1 + \rho_2 \frac{T_s}{1-z^{-1}} + \rho_3 \frac{1-z^{-1}}{T_s}

以上をコードにすると，以下のようになります。
VRFTのように制御器がパラメータに対して線形とは限らないため、今回は無名関数(lambda式)を使って制御器を表しています。

frit.m
% サンプリングタイムと演算子
Ts = 0.001;
s = tf('s');        % ラプラス演算子 s
z = tf('z', Ts);    % 時間進み演算子 z

% 参照モデル Td
tau = 0.02;
Td = c2d(1/(tau*s + 1), Ts);    % ゼロ次ホールドで離散化した一次遅れ系

% 制御器構造 C(rho)
Crho = @(rho) rho(1) + rho(2)*Ts/(1-z^-1) + rho(3)*(1-z^-1)/Ts; % PID制御器

% 初期制御器のパラメータ
rho0 = [10, 0.0, 0.0];              % 適当な比例制御器（安定化する）

% 初期制御器 C0
C0 = Crho(rho0);
frit.py
# サンプリングタイムと演算子
Ts = 0.001
s = ctl.tf([1,0], [1])         # ラプラス演算子 s
z = ctl.tf([1, 0], [1], Ts)    # 時間進み演算子 z

# 参照モデル Td
tau = 0.02
Td = ctl.c2d(1/(tau*s + 1), Ts)    # ゼロ次ホールドで離散化した一次遅れ系

# 制御器構造 C(rho)
Crho = lambda rho: rho[0] + rho[1]*Ts/(1-z**-1) + rho[2]*(1-z**-1)/Ts # PID制御器

# 初期制御器のパラメータ
rho0 = np.array([10, 0.0, 0.0])              # 適当な比例制御器（安定化する）

# 初期制御器 C0
C0 = Crho(rho0)

入出力データの取得

次に，制御対象から入出力データ $u_0(t), y_0(t)$ を取得します。
FRITの場合には，以下の条件を満たすようにデータを取得します。

  • 制御対象を安定化させる初期制御器 $C_0(z)$ を用いた時の閉ループ応答
  • 入力信号はステップ応答でもよい7

前回のVRFTと比較すると，閉ループ実験が可能であるため暴走の危険性を抑えることができます。
ただし，元々存在する制御器をより良い制御器に調整することになるため，初期制御器を得るために試行錯誤が必要となる可能性があります。
例えば、倒立振子を安定化させる初期制御器を用意することはそれなりに難しいことが想像できるかと思います。

今回の制御対象は前回と同様に，1次系で表されるモータモデル $P(s)$ を離散化して用います。

P(s) = \frac{K_p}{T_p s + 1}

なお，$K_p, T_p$ の値は，前回と同様にmanao様の記事からお借りしました。

以上を踏まえると、以下のようなコードで入出力データの取得が可能です。

frit.m
%データ取得に用いる入力信号 r  (ステップ信号)
N = 1000;           % データ数
r0 = ones([N, 1]);  % 信号のベクトル

% 制御対象モデル P
Tp = 0.74;
Kp = 1.02;
P = c2d(Kp/(Tp*s + 1), Ts);

% 初期の閉ループシステム
T0 = feedback(C0*P, 1);

% 制御対象の出力信号 y0
y0 = lsim(T0, r0);  

% 制御入力信号 u0
u0 = lsim(C0, r0 - y0);
frit.py
# データ取得に用いる入力信号 r (ステップ信号)
N  = 1000           # データ数
r0 = np.ones(N)     # 信号のベクトル

# 制御対象モデル P
Tp = 0.74
Kp = 1.02
P = ctl.c2d(Kp/(Tp*s + 1), Ts)

# 初期の閉ループシステム
T0 = ctl.feedback(C0*P, 1)

# 制御対象の出力信号 y0
y0, t0, _ = ctl.lsim(T0, r0)

# 制御入力信号 u0
u0, _, _ = ctl.lsim(C0, r0 - y0.flatten())

アルゴリズムに従って最適化計算を解く

最後に，FRITのアルゴリズムに従って時系列信号を生成し，最適化計算を解きます。

FRITもVRFTと同様に参照モデルに近い応答を実現することを目的とします。
これは，評価関数 $J_\mathrm{MR}(\boldsymbol{\rho})$ の最小化問題として表せます。

\begin{align}
J_\mathrm{MR}(\boldsymbol{\rho}) &= \left\| \left( \frac{P(z) C(z, \boldsymbol{\rho})}{1 + P(z) C(z, \boldsymbol{\rho})} - T_d(z) \right) W(z) \right\|_2 ^2
\end{align}

ここで，$\boldsymbol \rho$ は前述の通り制御器パラメータを表しています。
この評価関数を，VRFTと同様に制御対象の数式モデル $P(z)$ を用いずに，入出力データのみを用いて書き直します。
今回も理論的な説明は省略して結果だけを示すと，先ほどの評価関数 $J_\text{MR}({\boldsymbol\rho})$ を最小化する問題は，以下の $J_\text{FR}({\boldsymbol\rho})$ を最小化する問題と等価となります。

\begin{align}
J_\text{FR}({\boldsymbol\rho}) &= \left\| 
    y_L(t) - \tilde{y}(t, \boldsymbol{\rho})
\right\|^2
\end{align}

ここで、時系列データ $y_L(t)$ と $\tilde{y}(t, \boldsymbol{\rho})$ はパラメータを持つ制御器 $C (z, \boldsymbol{\rho})$を利用することで、以下のように生成可能です。

\begin{align}
u_L(t)       &= W(z)\ u_0(t)\\
y_L(t)       &= W(z)\ y_0(t)\\
\tilde{r}(t, \boldsymbol{\rho}) &= C(z, \boldsymbol{\rho})^{-1} \ u_L(t) +y_L(t) \\
\tilde{y}(t, \boldsymbol{\rho}) &= T_d(z)\ \tilde{r}(t)
\end{align}

ただし、制御器$C(z, \boldsymbol{\rho})$ は可逆であると仮定して記述しました。
このように変形することで、あるパラメータ $\boldsymbol{\rho}$ に対して入出力データのみを用いて評価関数 $J_\text{FR}$ を記述できます。
ただし、この最適化問題は非線形であるため非線形最適化が必要です。

元論文ではガウスニュートン法を用いた解法が述べられていますが、今回はお手軽に非線形ソルバーを利用します。
今回は、matlabではfmincon、pythonではscipyを利用して制約付き非線形最適化問題を解きました。

以上より、最適化問題を解く部分は以下のようなコードとなります。
(Optimization toolboxがない場合は、switch文を切り替えることで動作します)

frit.m
% 最適化問題の評価関数 f(x)
f = @(x) Jfrit(Crho(x), x, y0, u0, Td);

global C_ideal;     % 理想制御器
global fun;         % パラメトライズされた制御器

C_ideal = minreal(Td/(1 - Td)/P);
fun     = Crho;

% 最適なパラメータ rho
switch 3
    case 1
        % fminsearch を利用（MATLAB組込み）
        opt = optimset(...
            'Display', 'iter',...
            'PlotFcns', @optimplotfval,...
            'OutputFcn', @outfun);
        [rho, ~, ~, info] = fminsearch(f, rho0, opt);
    case 2
        % fminunc を利用（Optimization toolbox）
        opt = optimoptions('fminunc',...
            'MaxIterations', 400,...
            'Display', 'iter',...
            'PlotFcn', 'optimplotfval',...
            'OutputFcn', @outfun);
        [rho, ~, ~, info] = fminunc(f, rho0, opt);
    case 3
        % fmincon を利用（Optimization toolbox）
        opt = optimoptions('fmincon',...
            'Display', 'iter',...
            'PlotFcn', 'optimplotfval',...
            'OutputFcn', @outfun);
        [rho, ~, ~, info] = fmincon(f, rho0,...
            [], [], [], [], zeros(size(rho0)), inf(size(rho0)), [], opt);
end

% 設計した制御器 C
C = Crho(rho);  % 制御器を求める

% 評価関数 Je
Je0 = Jfrit(C0, rho0, y0, u0, Td);      % 初期制御器の評価値
Je  = Jfrit(C, rho, y0, u0, Td);        % 設計した制御器の評価値
disp("J_frit(C_0) = " + num2str(Je0));
disp("J_frit(C_opt) = " + num2str(Je));
frit.py
# 最適化問題の評価関数 f(x)
f = lambda x: Jfrit(Crho(x), x, y0, u0, Td)
C_ideal = ctl.minreal(Td/(1 - Td)/P)

# 制約条件（すべてのパラメータが正）
cons = LinearConstraint(
    np.eye(rho0.size), 
    np.zeros_like(rho0), 
    np.full_like(rho0, np.inf))

# 最適なパラメータ rho
optResult = minimize(f, rho0,
                     method="trust-constr", 
                     jac="2-point",          # 勾配関数
                     hess=BFGS(),            # ヘシアンの推定方法
                     constraints=cons,
                     options={"maxiter":np.inf, "disp":True},
                     callback=callbackFunc
                     )
rho = optResult["x"]

# 設計した制御器 C
C = Crho(rho)  # 制御器を求める

# 評価値
print("初期の評価値\t： {:5.3f}".format(f(rho0)))
print("設計後の評価値\t： {:5.3f}".format(f(rho)))

性能の確認

上記の手順で、今回もなんらかの制御器が得られたようです。
得られた制御器のパラメータ $\boldsymbol{\rho}$ は以下の通りです。
VRFTと同様に、MATLAB(fmincon)とPythonでほぼ同じ結果が得られていることが分かります。
一方で、fminsearchではPゲインだけ調整したようです。
非線形最適化はこのように局所最適解に落ち着いてしまうことがあるのが難しいところです。

初期制御器 MATLAB
(fmincon)		 MATLAB
(fminsearch)		 Python 理論値
比例ゲイン $K_p$ $10.0$ $35.4$ $47.8$ $35.4$ $36.3$
積分ゲイン $K_i$ $0.00$ $47.8$ $0.00$ $47.8$ $49.0$
微分ゲイン $K_d$ $0.00$ $0.00$ $0.00$ $0.00$ $0.00$
評価値 $J_\text{FR}$ $24.4$ $0.00$ $0.35$ $0.00$ $0.00$

最後にステップ応答とボード線図を確認しておきましょう。
以下のコードで確認できます。

frit.m
% 制御器を実装したシステム全体 G
G = minreal(feedback(P*C, 1));

% % ステップ応答
fig1 = figure('name', 'Step plot');
stepplot(G, Td);

%ボード線図表示
fig2 = figure('name', 'Bode plot of controller');
bodeplot(G, Td, {1,100});
frit.py
# 制御器を実装したシステム全体 G
G = ctl.minreal(ctl.feedback(P*C, 1), verbose=False)

# ステップ応答
plt.figure()
plt.title("Step response of closed loop system")
timeRange = np.arange(0, 0.12 + Ts, Ts)
ym, _ = ctl.step(Td, timeRange)
yg, _ = ctl.step(G, timeRange)
plt.plot(timeRange, ym, timeRange, yg)
plt.xlabel("Time [s]")
plt.ylabel("Velocity [V]")
plt.legend(['Reference model', 'Closed loop system'], loc='lower right')

# ボード線図表示
plt.figure()
plt.title("Bode plot of closed loop system")
ctl.bode(Td, G)
plt.legend(['Reference model', 'Closed loop system'], loc='lower left')

plt.show()

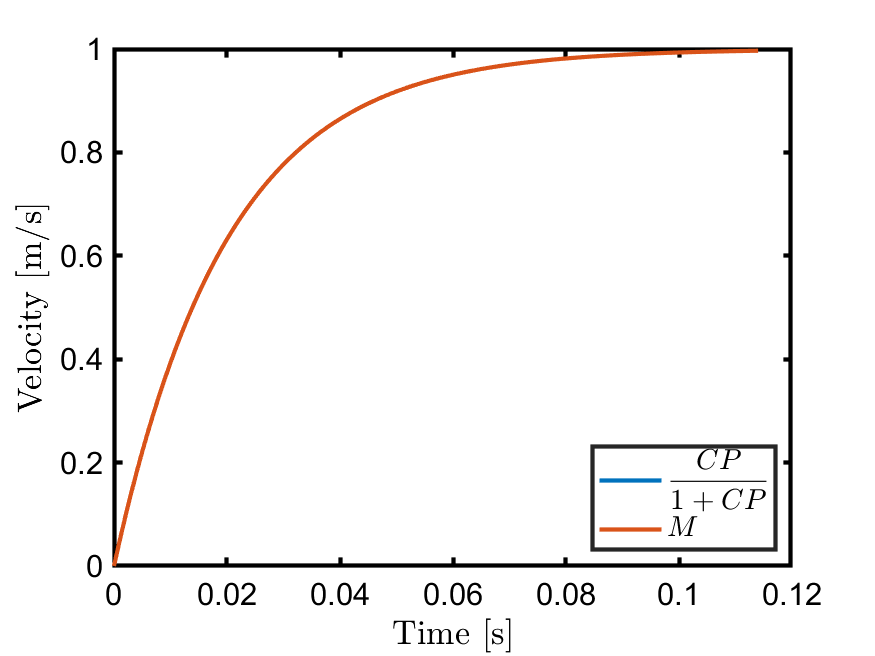
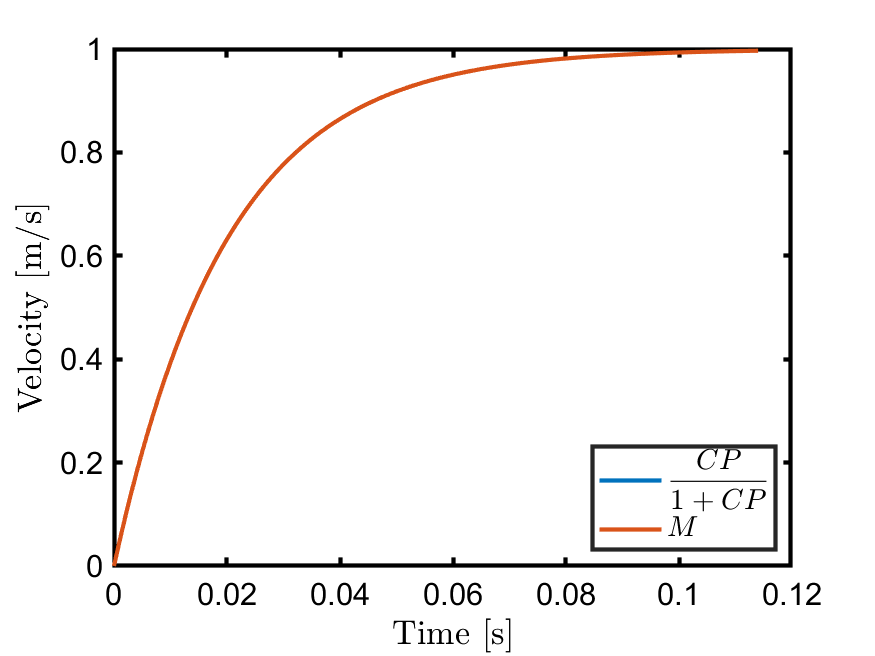
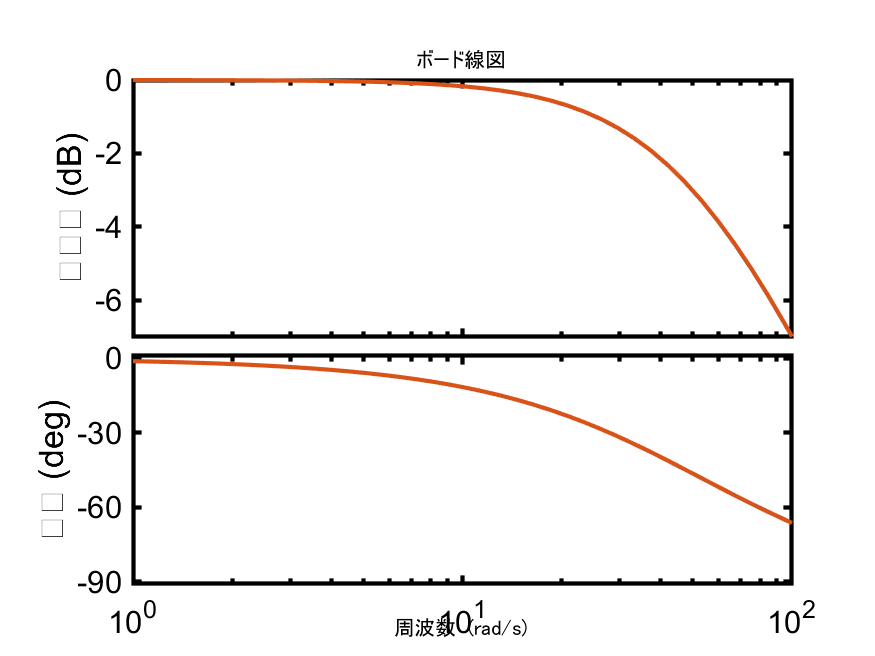
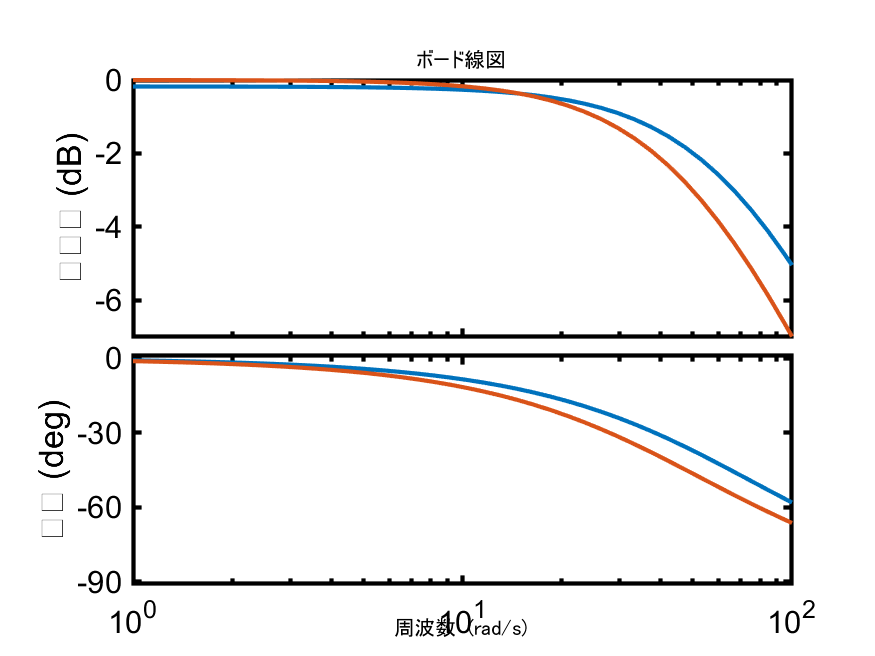
ここでは、fminconとfminserchのステップ応答と閉ループのボード線図をそれぞれ掲載しておきます。
fminsearchの結果を見ると高周波では参照モデル$T_d(z)$との差異がありますが、ステップ応答ではそこまで差はないことが分かります。

fmincon fminsearch
stepFritFmincon.png stepFritFminserch.png
bodeFritFmincon.png bodeFritFminserch.png

全体のコード

動作する完全なコードは 私のgithub を参照してください。(MATLAB版 / Python版)

おわりに

今回も理論はがっつり省略しつつ、前回のVRFTと対応付けながらVRFTについて紹介しました。
VRFTと比較すると、閉ループでのデータ取得が可能かつ調整できる制御器の自由度が高い点で利点があります。
一方で、制御器の構造の決定や非線形最適化に伴う難しさがあると言えるでしょう。

この記事でデータ駆動型制御に興味を持って頂けましたら幸いです。
気になる点などございましたら、お気軽にコメントして頂ければと思います。

P.S.

興味を持ってくださった方は、こちらの特集記事を見てもらうと面白いトピックが見つかるかもしれません。
来年は雑音を考慮した手法を紹介できるといいなぁ(NCbTとか)と思ってます。

参考文献

  1. FRITの原著論文（金子先生他）
  2. FRITの解説記事（金子先生）
  3. MATLABによる非線形最適化（MATLAB公式）
  4. Scipyによる最適化のまとめ（alchemistさまの記事）

  1. 数学的な問題としては，理想制御器が実現できない場合には，$J_{\rm MR}({\boldsymbol\rho})$と$J_{\rm VR}^{N}({\boldsymbol\rho})$の評価が漸近的に等価にはならないという問題などがあるそうです。 ↩

  2. これはシステム同定とも共通する問題です。 ↩

  3. 文脈によっては「制御器設計」と「制御器調整」が，初期制御器の有無で明確に区別されます。 ↩

  4. コードを書き換えることで、MATLAB組み込みのソルバーでもコードは動作します。 ↩

  5. interpreterをlatexからnoneに書き換えることで、数式は表示されませんがコードは動作します。 ↩

  6. 論文に合わせて$T_d$としましたが，VRFTの$M$と同じ仕様です。 ↩

  7. もちろん厳密には初期データのPE性(≒周波数特性)は最適化の結果に影響します。しかし、精々追従させたい目標値応答と同じ程度の情報が含まれていればよいと述べられています。(ステップ応答性能が欲しいなら、初期データもステップ応答で取得する等) ↩

23
17
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
23
17