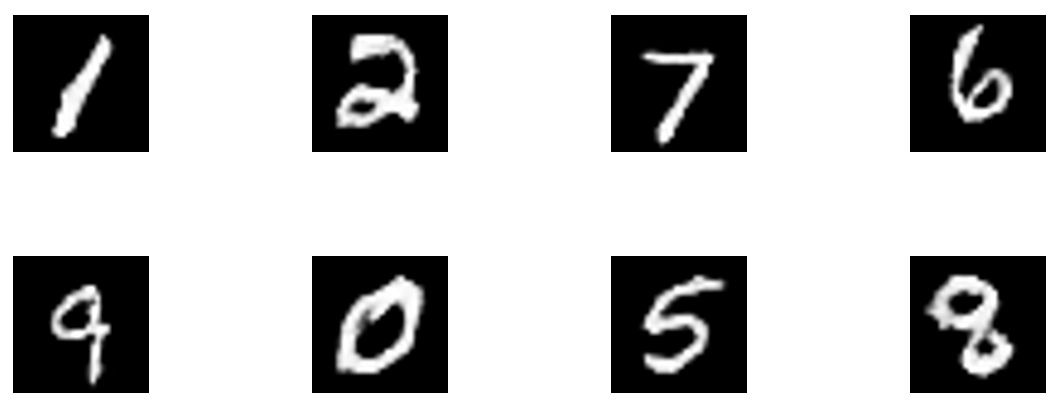想定読者
- GAN (Generative adversarial network)の概要を理解している人
- 分類モデルなどの基本的な学習を実装したことがある
- GANを実装したことがある、あるいは実装しようと思っている人
手前味噌ですが、GANの概要をこちらの記事でまとめています。
はじめに
GANはGeneratorとDiscriminatorの2つのネットワークが競合して1つの目的関数を最適化するアルゴリズムですが、Chainer, PyTorchなどのディープラーニングライブラリで実装しようとすると一筋縄では行かないと思います。
分類や回帰であれば 入力→出力→損失 のように計算の流れが一本になっているので、データとモデルさえ用意すればライブラリの機能で学習は自動で回してくれます。
しかし、GANでは
- モデルが2つある
- それぞれに対して損失を計算する
- 片方は損失を大きくする、もう一方は損失を小さくする
といった違いがあるのでOptimizerを2つ用意して、学習部分も自分で書かなければなりません。
しかし、Gradient reversal layer (GRL)1を利用するとモデルの定義を工夫するだけでGeneratorとDiscriminatorを単一のモデルとして扱うことができるようになります。
すると1個のOptimizerだけで済み、計算フローが 入力(乱数ベクトル)→出力→損失 と分類や回帰のようになるので学習部分はライブラリに投げられるようになり、コードが簡潔になります。
Gradient reversal layer (GRL)
GRLはForward計算のときには何もしませんが、Backwardの時だけ勾配の符号を反転するレイヤーです。
\begin{align}
\mathcal{R}({\bf x})&={\bf x}\\
\frac{d\mathcal{R}}{d{\bf x}}&=-{\bf I}
\end{align}
役割としてはこれだけです。
そもそもGANの実装がややこしくなるのは、Generator(以下$G$、パラメータ$\theta_G$)とDiscriminator(以下$D$、パラメータ$\theta_D$)が同じ目的関数を逆方向に最適化しようとするからです。
\max_{\theta_G} \min_{\theta_D} V(\theta_G,\theta_D) \\
V(\theta_G,\theta_D)=\mathbb{E}_{{\bf x}\sim p_t}\left[\log D({\bf x}) \right] +\mathbb{E}_{{\bf z}\sim p_{\bf z}}\left[ \log (1-D(G({\bf z}))) \right]
上式では$D$は本物に対して0に近い値を、$G$が生成した偽物に対しては1を出力するように学習します。
対して$G$は$D$が0を出力するような画像を生成するように学習します。
そこで、図のように$G$の生成データをGRLに通してから$D$に入力するようにしてみます。
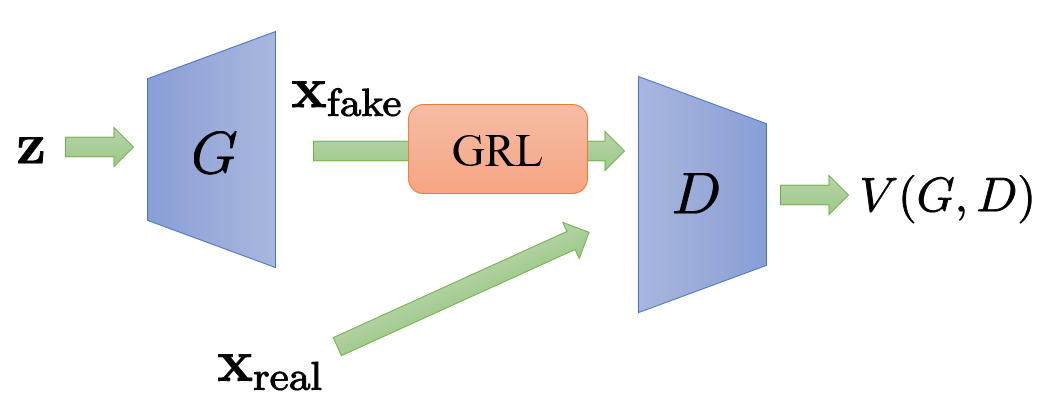
すると、目的関数が
V(G,D)=\mathbb{E}_{{\bf x}\sim p_t}\left[\log D({\bf x}) \right] +\mathbb{E}_{{\bf z}\sim p_{\bf z}}\left[ \log (1-D({\cal R}(G({\bf z})))) \right]
となり、$\theta_G$に対する勾配はGRLによって符号が反転します。
\begin{align}
\frac{\partial V}{\partial \theta_G}&=\frac{\partial V}{\partial {\cal R}({\bf x}_\text{fake})} \frac{\partial {\cal R}({\bf x}_\text{fake})}{\partial {\bf x}_\text{fake}} \frac{\partial {\bf x}_\text{fake}}{\partial \theta_G} \\
&=-\frac{\partial V}{\partial {\cal R}({\bf x}_\text{fake})} \frac{\partial {\bf x}_\text{fake}}{\partial \theta_G}
\end{align}
一方で$\theta_D$に対する勾配はGRLがあってもなくても$\partial V/\partial \theta_D$で一緒です。
したがって、異なる方向の最適化だったのがGRLによって、同じ方向の最適化になります。
\min_{\theta_G} \min_{\theta_D} V(\theta_G,\theta_D) = \min_{\theta_G,\theta_D}V(\theta_G, \theta_D)
よって、$G$と$D$を単一のモデルとみなしてまとめて一つのOptimizerで最適化できます!
実装
PyTorchで実装しました。(適当に省略しているのでそのままでは動きません)
全体のコードはGitHubにあります。
GRL
import torch
import torch.nn.functional as F
from torch import Tensor, nn
import numpy as np
class GradientReversalLayer(torch.autograd.Function):
@staticmethod
def forward(ctx, input):
return input
@staticmethod
def backward(ctx, grad_output):
return -grad_output
def gradient_reversal_layer(x: Tensor) -> Tensor:
return GradientReversalLayer.apply(x)
モデル
class GAN(nn.Module):
def __init__(self, zdim, device="cpu"):
super().__init__()
self.zdim = zdim
self.device = device
self.gen = get_generator(zdim)
self.dis = get_discriminator()
def forward(self, x_real):
z = np.random.uniform(size=(len(x_real), self.zdim)).astype(np.float32)
z = torch.from_numpy(z).to(self.device)
x_fake = self.gen(z)
y_fake = self.dis(gradient_reversal_layer(x_fake))
y_real = self.dis(x_real)
loss_fake = F.softplus(y_fake).mean()
loss_real = F.softplus(-y_real).mean()
return loss_fake, loss_real
こうしてしまえば、学習は既存の枠組みでできるようになります。
model = GAN()
opt = torch.optim.Adam(model.parameters())
dataloader = DataLoader(dataset)
for e in range(epoch):
for x_real in dataloader:
model.train()
opt.zero_grad()
loss_fake, loss_real = GAN(x)
(loss_fake + loss_real).backward()
opt.step()
結果
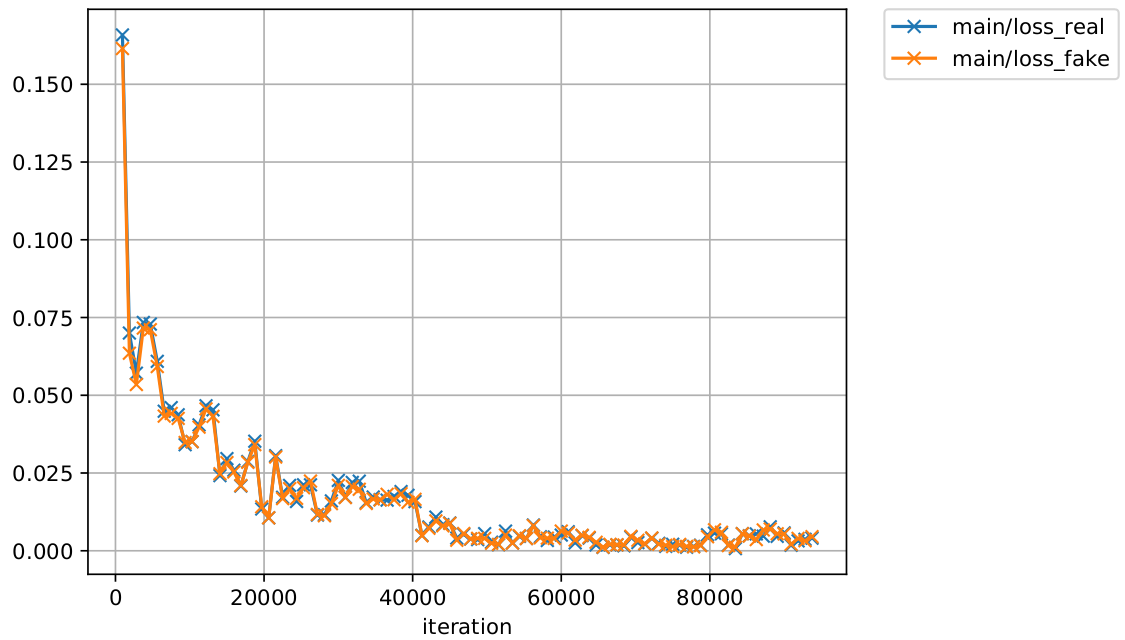
上手く行ってそうです。
ロスの推移に$G, D$の拮抗が垣間見えます。
おわりに
Backwardの時だけ勾配を反転することで$G, D$の最適化の方向を揃えてまとめて最適化できるようになりました。
-
Ganin, Yaroslav, et al. "Domain-adversarial training of neural networks." The Journal of Machine Learning Research 17.1 (2016): 2096-2030. ↩