はじめに
「機械学習の数理 Advent Calendar 2018」の17日目の記事です。
Generative adversarial network (GAN)の実装方法をGitHubなどであちこち調べてみると,損失関数の計算の仕方が複数あることに気付きます。
以前初めてGANの論文を読んで実装しようとした際に戸惑ったので,論文と実装のギャップを埋めるつもりでまとめました。
GANとは?
GANについて簡単に説明します。
GANくらい知ってるよ!という方は飛ばすことをおすすめします。
概要
GANは教師なし学習の一種です。
訓練データの確率分布$p_t(x)$を学習して,訓練データにありそうな新たなデータを生成するための手法です。
学習にはGenerator $G$,Discriminator $D$という2つのニューラルネットワークが登場します。
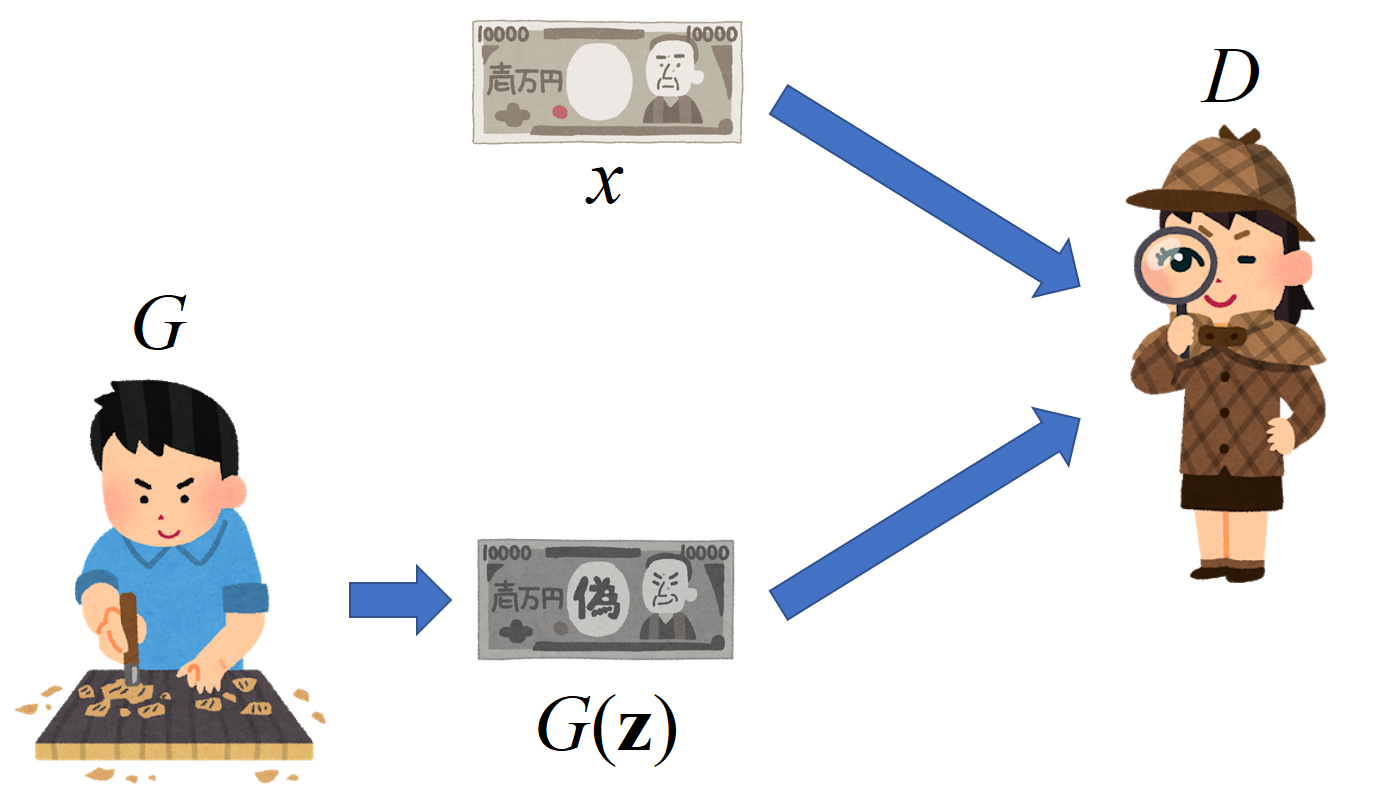
$G$は偽札職人によく例えられ,乱数ベクトル${\bf z}\sim p_{\bf z}({\bf z})$から訓練データにありそうなデータ$G({\bf z})$を生成します。
対して$D$は警察に例えられます。つまり,与えられたデータ$x$が$G$により生成された偽物なのか,訓練データから取ってきた本物なのかを判別します。
$G$は$D$に見破られないように,$D$は$G$を見破れるように競合して学習することで本物に近いデータが生成できるようになります。
実際に,上手く学習させることでイラストの生成などもきれいにできるようになります。
具体的には,以下の損失関数を$D$に関して最大化,$G$に関して最小化することで最適な生成器$G^\ast$が得られます。
\begin{align}
G^\ast&={\rm arg}\min_G \max_D V(G,D) \\
V(G,D)&=\mathbb{E}_{x\sim p_t(x)} \left[ \log D(x) \right] + \mathbb{E}_{{\bf z}\sim p_{\bf z}({\bf z})} \left[ \log\left( 1-D\left( G({\bf z}) \right) \right) \right]
\end{align}
G, Dの最適解
このアドベントカレンダーの趣旨として数理的な側面に触れてみます。ここから少し上式の最適解について考えてみたいと思います。
論文に書いてある内容ですが,自分用に少しだけ丁寧に式変形をやっていきます。
損失関数の実装の方に興味がある方は飛ばすことをおすすめします。
まず,$G$を固定したときの$D$の最適解$D^\ast_G$について考えます。
上に書いた$V(G,D)$の式より,期待値の$\mathbb{E}$を書き直すと
V(G,D)=\int_x p_t(x)\log D(x)dx + \int_{\bf z} p_{\bf z}({\bf z})\log \left(1-D(G({\bf z})) \right)d{\bf z}
とできます。
ここで,乱数ベクトル${\bf z}\sim p_{\rm z}$から$G$が生成するデータの分布を$p_g(x)$とします。これを使って${\bf z}$の積分を書き換えると,
V(G,D)=\int_x \left\{ p_t(x)\log D(x) + p_g(x)\log \left( 1-D(x) \right) \right\}dx\;\;\cdots ☆
となります。
$V(G,D)$を最大化するには積分の中身を最大化すれば良いので,中身を$D(x)$で微分します。
\frac{p_t(x)}{D(x)} - \frac{p_g(x)}{1-D(x)}
これが0になるような$D(x)$が最適解なので,
D^\ast_G(x)=\frac{p_t(x)}{p_g(x)+p_t(x)}
となります。
次に,$G$の最適解について考えます。
☆で$V(G,D)$に$D$の最適解$D^\ast_G$を代入すると,
\begin{align}
V(G,D^\ast_G)&=\int_x \left( p_t\log \frac{p_t}{p_g+p_t}+p_g \log \frac{p_g}{p_g+p_t} \right) dx \\
&= \int_x \left\{ p_t \log \left( \frac{1}{2}\frac{p_t}{\frac{p_g+p_t}{2}} \right) + p_g \log \left( \frac{1}{2}\frac{p_g}{\frac{p_g+p_t}{2}} \right) \right\} dx \\
&= \int_x p_t \log \frac{p_t}{\frac{p_g+p_t}{2}} dx + \int_x p_g \log \frac{p_g}{\frac{p_g+p_t}{2}}dx - \int_x (p_t+p_g)\log 2 dx \\
&= D_{KL}\left( p_t \left| \left| \frac{p_g+p_t}{2} \right. \right. \right) + D_{KL}\left( p_g \left| \left| \frac{p_g+p_t}{2} \right. \right. \right) -\log 4 \\
&= 2D_{JS}\left( p_t || p_g \right) -\log 4
\end{align}
となります。
つまり,$D_G^\ast$のもとでの$G$の最適化はJensen-Shannonダイバージェンスの最適化になる事が分かります。
$D_{JS}\left( p_t || p_g \right)$は$p_g=p_t$のときに最小値0を取るので,これが$G$の唯一の最適解です。
このとき損失$V(G,D_G^\ast)$は最小値$-\log 4$になります。
いろいろな計算方法
損失関数$V(G,D)$の計算の仕方について,上述の式を見たままに実装されている場合が少なかったため,論文と実装のギャップを埋めるつもりでまとめました。
以下の説明では損失関数は**$D$について最大化,$G$について最小化**する対象としています。
例として挙げたリポジトリの実装とは符号が異なっている場合があるので注意してください。
シグモイド→バイナリクロスエントロピー
$D$の出力の活性化関数をシグモイドとし,バイナリクロスエントロピー関数で損失を計算します。
$D$の入力が本物であれば1,$G$が生成した偽物であれば0のラベルと比較します。
$D$の出力を$D(x)$,参照ラベルを$t\in \{ 0,1\}$とすると,バイナリクロスエントロピーは
{\cal L}_{BCE}=\mathbb{E}\left[ t\log D(x) + (1-t)\log (1-D(x)) \right]
で計算されます。
これは本物($t=1$)に対しては${\cal L}=\mathbb{E}_{x\sim p_t}[ \log(D(x)) ]$,
偽物($t=0$)に対しては${\cal L}=\mathbb{E}_{{\bf z}\sim p_{{\bf z}}}[ \log(1-D(G({\bf z})))]$となるので,最初に示したオリジナルの損失関数と同じであることが分かります。
以下の記事やリポジトリでこの式による実装がされていました。
ソフトマックス→クロスエントロピー
この実装では$D$の判別をクラス分類問題と捉えます。
$D$の出力を2次元のベクトルにし,それぞれの次元が本物・偽物の確率を表すように学習します。
$D$の出力層の活性化関数にはソフトマックス関数を使用します。
本物か偽物かのラベルもベクトルとなるので,
{\bf t}=[t_{\rm fake}, t_{\rm real}]\in \{ [0,1], [1,0] \}
と表現します。
$D$の出力${\bf y}=[y_{\rm fake}, y_{\rm real}]$とのクロスエントロピーを計算すると,
{\cal L}_{softmax}=\mathbb{E}\left[ t_{\rm fake}\log y_{\rm fake}+t_{\rm real} \log y_{\rm real} \right]
となります。
実は,これはSoftmax GANと呼ばれる手法です。
数式的にはオリジナルのGANとは異なっています。
以下のリポジトリでこれを使った実装がされていました。
ソフトプラス
初めて見たときにこれが一番謎でした。
先の2つとは異なり,$D$の出力に活性化関数を適用しません。
そして,損失を以下で計算します。
{\cal L}_{softplus}=\mathbb{E}_{x\sim p_t}\left[ {\rm softplus}(D(x)) \right]+\mathbb{E}_{\tilde{x}\sim p_g}\left[ {\rm softplus}(-D(\tilde{x})) \right]
ソフトプラスは以下のような関数で,ReLUの角を丸めたような形状をしています。
{\rm softplus}(y)=\log (1+\exp (y))
上記のようなクロスエントロピーを使う計算方法とは全く異なるように見えますが,実は1つ目の方法と等価です。
$D(x)$を活性化関数を通す前の出力,シグモイド関数を$\sigma(x)=1/(1+\exp (-x))$とすると,1つ目の損失関数は
{\cal L}_{BCE}=\mathbb{E}\left[ t\log \sigma(D(x)) + (1-t)\log (1-\sigma(D(x))) \right]
ここで,$x$が本物の場合と偽物の場合に分けて考えます。
$x$が本物の時,$t=1$なので最初の項だけが残ります。
したがって,本物のデータに対する損失は
\begin{align}
{\cal L}_{BCE}^{real}&=\mathbb{E}_{x\sim p_t}\left[ \log \sigma (D(x)) \right] \\
&= \mathbb{E}_{x\sim p_t}\left[ \log \frac{1}{1+\exp(-D(x))} \right] \\
&=-\mathbb{E}_{x\sim p_t}\left[ (1+\exp(-D(x))) \right] \\
&=-\mathbb{E}_{x\sim p_t}\left[ {\rm softplus}(-D(x)) \right]
\end{align}
$x$が偽物のときには$t=0$なので2番目の項が残ります。
このとき,
\begin{align}
{\cal L}_{BCE}^{fake}&=\mathbb{E}_{\tilde{x}\sim p_g}\left[ \log(1-\sigma(D(\tilde{x}))) \right] \\
&= \mathbb{E}_{\tilde{x}\sim p_g}\left[ \log\left( 1-\frac{1}{1+\exp(-D(\tilde{x}))} \right) \right] \\
&= -\mathbb{E}_{\tilde{x}\sim p_g}\left[ \log (1+\exp(D(\tilde{x}))) \right] \\
&=-\mathbb{E}_{\tilde{x}\sim p_g}\left[ {\rm softplus}(D(\tilde{x})) \right]
\end{align}
結局,シグモイド→バイナリクロスエントロピーの合成関数がソフトプラスになっていることが分かります。
以下のリポジトリでこの実装がされていました。
おわりに
GANの簡単な説明と,損失関数の3つの異なる実装の仕方を紹介しましたが,1つ目と3つ目は数学的には等価なものでした。
どの実装をしても学習はできますが,個人的には3つ目のソフトプラスを用いた実装が元の数式と等価でかつスマートなので良いと思いました。
参考
- Goodfellow, Ian, et al. "Generative adversarial nets." Advances in neural information processing systems. 2014.
- Lin, Min. "Softmax GAN." arXiv preprint arXiv:1704.06191 (2017).
- Chainerで顔イラストの自動生成
- chainerのtrainer機能を使ってDiscoGANを実装した
- carpedm20/DCGAN-tensorflow
- はじめてのGAN
- eriklindernoren/PyTorch-GAN
- mattya/chainer-DCGAN
- chainer/chainer
- Simple implementation of Generative Adversarial Nets using chainer