結論
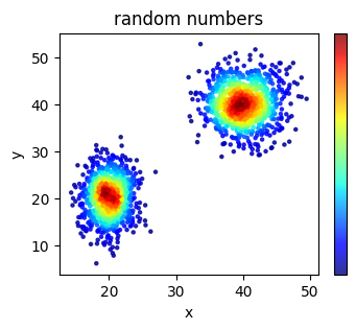
こんな感じで、散布図の各プロットにおいて密度を色で表現する。

※実行環境:Google Colaboratory
コード全体のみ見たい場合
2024.01.27追記
カーネル密度推定の高速化方法をまとめました。
【方法1】scipy.statsを使う
乱数での実装例
まずはライブラリーのインポートと乱数の生成。
from scipy.stats import gaussian_kde
import numpy as np
# 乱数の生成
x1 = np.random.normal(20, 2, 1000)
y1 = np.random.normal(20, 4, 1000)
x2 = np.random.normal(40, 3, 1000)
y2 = np.random.normal(40, 4, 1000)
np.vstackで[x1, y1]および[x2, y2]を縦方向で結合する。
次に、gaussian_kdeクラスを用いてカーネル密度推定(kernel density estimation; KDE) を計算する。詳しい使い方については、他のサイトや公式ドキュメントを参照してください。
xy1 = np.vstack([x1, y1])
z1 = gaussian_kde(xy1)(xy1)
xy2 = np.vstack([x2, y2])
z2 = gaussian_kde(xy2)(xy2)
密度が計算されたので、あとはplt.scatterで散布図を描画して各プロットの色に密度を指定する。
-
c(色):に密度を指定する。 -
cmap(カラーマップ):好みなので'jet'を指定。
その他にも、カラーバーやタイトル、軸タイトルの表示などを設定。
# 散布図を作成
plt.figure(figsize=(4, 3))
plt.scatter(x1, y1, c=z1, s=5, marker='o', cmap='jet', alpha=0.8)
plt.scatter(x2, y2, c=z2, s=5, marker='o', cmap='jet', alpha=0.8)
# カラーバーを追加
cb = plt.colorbar(ticks=mticker.NullLocator())
# ラベルを設定
plt.title('random numbers')
plt.xlabel('x')
plt.ylabel('y')
# プロットを表示
plt.show()
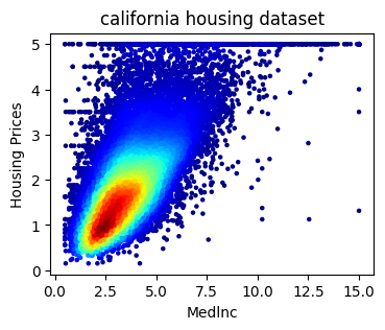
california housing datasetでの実装例
scikit-learnのcalifornia housing datasetを読み込む。
from sklearn.datasets import fetch_california_housing
california_data = fetch_california_housing()
配列xにMedlnc(世帯所得の中央値)、配列yにHousePrices(住宅価格)を入れる。
2つの配列を結合した後、KDEを計算する。
x = california_data.data[:,0] #Medlnc(世帯所得の中央値)
y = california_data.target #HousePrices(住宅価格)
xy = np.vstack([x, y])
z = gaussian_kde(xy)(xy)
上と同様にプロットする。
# 散布図を作成
plt.figure(figsize=(4, 3))
plt.scatter(x, y, c=z, s=5, marker='o', cmap='jet', alpha=1)
#ラベルの表示
plt.xlabel('Medlnc')
plt.ylabel('Housing Prices')
# プロットを表示
plt.show()
実装1
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde
import numpy as np
import matplotlib.ticker as mticker
# 乱数の生成
x1 = np.random.normal(20, 2, 1000)
y1 = np.random.normal(20, 4, 1000)
x2 = np.random.normal(40, 3, 1000)
y2 = np.random.normal(40, 4, 1000)
# 密度プロットを追加
xy1 = np.vstack([x1, y1])
z1 = gaussian_kde(xy1)(xy1)
xy2 = np.vstack([x2, y2])
z2 = gaussian_kde(xy2)(xy2)
# 散布図を作成
plt.figure(figsize=(4, 3))
plt.scatter(x1, y1, c=z1, s=5, marker='o', cmap='jet', alpha=0.8)
plt.scatter(x2, y2, c=z2, s=5, marker='o', cmap='jet', alpha=0.8)
# カラーバーを追加
cb = plt.colorbar(ticks=mticker.NullLocator())
# ラベルを設定
plt.title('random numbers')
plt.xlabel('x')
plt.ylabel('y')
# プロットを表示
plt.show()
実装2
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde
import numpy as np
from sklearn.datasets import fetch_california_housing
california_data = fetch_california_housing()
x = california_data.data[:,0]
y = california_data.target
xy = np.vstack([x, y])
z = gaussian_kde(xy)(xy)
# 散布図を作成
plt.figure(figsize=(4, 3))
plt.scatter(x, y, c=z, s=5, marker='o', cmap='jet', alpha=1)
#ラベルの表示
plt.xlabel('Medlnc')
plt.ylabel('Housing Prices')
# プロットを表示
plt.show()
【方法2】sklearnを使う方法
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KernelDensity
from sklearn.datasets import make_blobs
パラメータの設定など詳しい使い方は公式ドキュメントを参照してください。
# ダミーデータの生成
np.random.seed(42)
data, _ = make_blobs(n_samples=10000, centers=2, random_state=42, cluster_std=1.0)
# KDEの設定
bandwidth = 0.2 # バンド幅を適切な値に調整することが重要です
kde = KernelDensity(bandwidth=bandwidth, metric='euclidean', kernel='gaussian')
# ダミーデータを用いてKDEを学習
kde.fit(data)
# データの密度を計算
density = np.exp(kde.score_samples(data))
# グラフで可視化
plt.scatter(data[:, 0], data[:, 1], c=density, cmap='jet', marker='o', alpha=0.8, s=1)
# カラーバーを追加
cbar = plt.colorbar()
cbar.set_label('Density')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
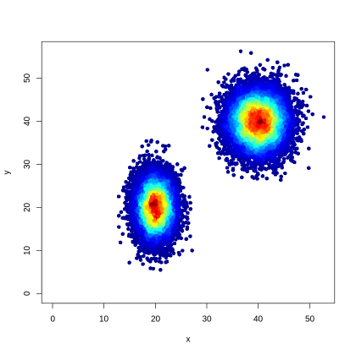
【おまけ】Rで実装する方法
Pythonに比べて圧倒的に手軽にできる。全て(乱数生成、密度推定、散布図の描画)においてパッケージを読み込む必要がなく標準搭載で実装できる。
あと、密度推定の処理速度もPythonに比べて段違いに速い。
x1 <- rnorm(10000, 20, 2)
y1 <- rnorm(10000, 20, 4)
x2 <- rnorm(10000, 40, 3)
y2 <- rnorm(10000, 40, 4)
jet_palette <- colorRampPalette(c("#00008F", "#0000FF", "#0080FF", "#00FFFF", "#80FF80", "#FFFF00", "#FF8000", "#FF0000", "#800000"))
col1 <- densCols(x1, y1, colramp = jet_palette)
col2 <- densCols(x2, y2, colramp = jet_palette)
plot(0, 0, type = "n", xlim = c(0, max(x1, x2)), ylim = c(0, max(y1, y2)),xlab = "x", ylab = "y")
points(x1, y1, col = col1, pch = 16)
points(x2, y2, col = col2, pch = 16)