Juliaで Unsupervised Kernel Regression 実装

この記事は古川研究室 Advent_calendar 5日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。

---

なんと，お知り合いのかたがまったく同じような記事を書いてました．ど，どちらも見ればより理解が深まると思います！
Juliaに入門して教師なしカーネル回帰を実装してみる

---

本記事ではUnsupervised Kernel Regression:UKR を概説して，アルゴリズム部分をJuliaで実装します．

概要

高次元のデータセットから低次元多様体を再構成することはデータマイニング，機械学習，統計学習理論において重要な課題である．¹

UKRは Principal Manifold学習のためのノンパラメトリックアプローチです．UKRはデータセットの潜在空間での表現（潜在変数）を獲得するため，また，潜在空間からオリジナルのデータ空間への滑らかな写像を獲得するためにNadaraya-Watson推定を使います²． UKRは直訳すると教師なしカーネル回帰です．古典的なカーネル回帰としてNadaraya-Watson推定をとりあげそれを教師なし学習に転用させています．Nadaraya-Watson推定については昨年のアドベントカレンダーで式の意味を解釈しようとしています．

問題設定

given:
$D$次元ベクトルの観測データ$\left(\mathbf{x}_n \right)$$ \in \mathcal{X} = \mathbb R^D$

estimate:
$y \simeq f(\mathbf{x})$となるような
$L(<D)$次元ベクトル潜在変数 $ \left(\mathbf{z}_n \right) \in \mathcal{Z} = \mathbb R^L$ と写像 $f:\mathcal{Z} \rightarrow \mathcal{X}$

目的関数

$ E (\mathbf{Z}) = \frac{1}{N} \sum_n || \mathbf{x}_n - f \left(\mathbf{z}_n; \mathbf{Z} \right) ||^2 $

ここで，
$f(\mathbf{z}) = \sum_n \frac{k(\mathbf{z}, \mathbf{z}_n)\mathbf{x}_n}{K(\mathbf{z})}$,

$K (\mathbf{z}) = \sum_j k(\mathbf{z}, \mathbf{z}_n)$,

$k(\mathbf{z}, \mathbf{\zeta}) = \exp({\frac{1}{2\sigma^2}|| \mathbf{z} - \mathbf{\zeta} ||^2})$

この目的関数を潜在変数$\mathbf{Z}$に関して最小化することで，潜在変数と写像を求めます．
なぜ潜在変数$\mathbf{Z}$ のみを推定すれば写像も推定するようになるんでしょう？（そこはまた別の記事で書く予定です．）

この目的関数を最小化には勾配法を使うことができ，今回は最急降下法を使います．

また，目的関数の最小化すると，潜在変数同士が無限遠に離れ合おうとする $\mathbf{z} \rightarrow \infty$　ので，学習が終了しないため，通常はRegularizationをかける必要があります．

また，元論文では回帰の文脈から導出しているので，データのことを$\mathbf{y}$, 潜在変数のことを$\mathbf{x}$と読んでいます（非常にごちゃ$^{10}$ になるので注意が必要です）

実装

今回はJuliaの自動微分を使って勾配を求めますが，論文では解析解もだしているのでそちらで実装することも可能です．

実装の流れとしては写像によりデータの推定値$(f(\mathbf{z_n}))$を作り，目的関数を作ってそれを自動微分を使って勾配をだすだけです．

データの作成

# パラメータの設定
N = 100
D = 3
L = 2
epoch = 200
eta = 0.1

true_z = rand(Float64, (N, L)) .* 2.0 .- 1.0
x1 = true_z[:,1]
x2 = true_z[:,2]
x3 = x1 .^2 - x2 .^2
# x = hcat(x1[:,:],x2[:,:],x3[:,:])
# x = [x1[:,:],x2[:,:],x3[:,:]]
x = hcat(x1,x2,x3)
size(x)
scatter(x1, x2, x3, marker=:circle)

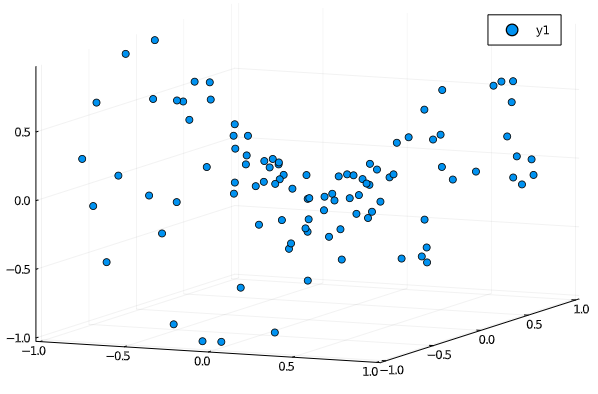
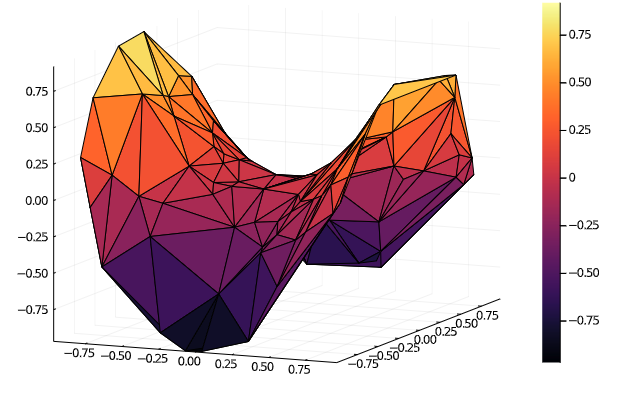
こうしてみるとわかりにくいですが，次のようにsurface表示するとわかりやすいかもです．こんな感じで2次元多様体のデータを用意しました．

潜在変数の初期化

潜在変数のスケールは$\sigma$より小さくする必要があるため，*0.01をかけています．

z = randn(Float64, (N, L)) * 0.01
scatter(z[:,1], z[:,2])

次に，$(f(\mathbf{z}_n))$をつくる式を作ります．

function f(z,x)
    R = exp.(-0.5 .* pairwise(SqEuclidean(),z,z,dims=1))
#     sum((z[1,:]-z[2,:]).^ 2)
    G = sum(R, dims=1)
#     print("G.shape:",size(G))
    R_tilde = broadcast(/,R,G)
#     print(sum(R_tilde,dims=2)) # 正規化とった方向に合計をとると1になるよね。
    Y = R*x
    return Y
end

次にE(Z)をつくります．

function E(z,x)
    estimated_x = f(z,x)
    E = sum(evaluate(SqEuclidean(),estimated_x,x)) 
    return E
end

じゃあ学習します．

for i in 1:epoch
    f(z) = E(z,x)
    z -= ForwardDiff.gradient(f,z) .* eta
end

f(z)をつくるのは，微分したいもののみを入力とした関数と微分したいものをjuliaの微分の式に入れる必要があるためです．回避する方法があったら教えてください．

結果

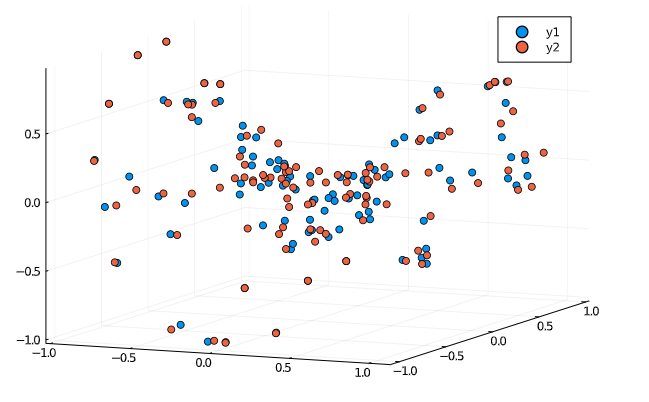
ちょっとわかりにくいですが，データ点（青）にデータの推定点（赤）が近くにきていて分布もだいたい似たようになっていることがわかります．おそらく（経験的に）学習はうまくいっているのですが，それを観察するためには，慣れない描画パッケージを使う必要がでてきそうだったのでひとまずこのへんで．

また，今回実装したコードは自分の Github(try_julia)にあがっています．パッケージのインポートとかも書いてるつもりです．

独り言

(主に普段pythonでtorchとかnumpyを使っている人として)

• 描画がめっちゃ楽（こだわるんだったら多分長くなりそう。まだ、アニメーションしてない。（ちょい大変らしい）matplotlibよりはわかりやすい。ただ、用意するのが重い）
• 若い言語なのにパッケージ充実（微分するやつ・Distつくるやつもある. pandasとかeinsumあるかはみてない（まあpythonのパッケージインポートできるからいいか））ので、UKRつくるくらいだったらOK。Julia自体が独自パッケージをいれやすいらしく開発が盛ん？jupyterで開発できるのもでかい。あと，Jupyterで開発できるのもでかいね〜
• 行列計算的にはBroadcastもあるし、行列 x スカラーのときは 演算子の前に . をつけるから可読性高くなってる気がする。好き。np.書かなくていいのも地味に楽な気が
• pythonからの移籍。pythonかける人なら簡単にうつれそう。3時間かからないくらいで書けた。（あとは数値計算の信頼度？）
• 困ったときのドキュメントは日本語でもそこそこある。
• 速度：早い気がするが？なんかjuliaはベクトル使うなとか、使えとか。namda使ったpythonが一番速いとかあるけど、素でforでもベクトルでもそこそこはやいのはかなりいい。(要検証)

総括

所感：個人的にはめっちゃ好き。今すぐ乗り換えたいくらい。なんか、書いてて気持ちいい。この処理はこういう感じに書きたいよね〜って感じ。(ex) Y = Broadcast(演算子, 行列、行列）みたいに書く。)そういう面で初心者もこっちのがいいと思う。むしろpythonはプロ向けな気がする。演算子が使えればいいくらいの最初の人はjuliaがおすすめな気がする。いやなところがあるとすれば，配列の１番目のインデックスが1スタート（0じゃない）

---

1. Christian Feuersänger,Michael Griebel, "Principal manifold learning by sparse grids",2009 ↩

2. Stefan Klanke, "Learning Manifolds with the Parametrized Self-Organizing Map and Unsupervised Kernel Regression, 2007 ↩