Batch Normalization(BatchNorm)の効果を畳み込みニューラルネットワーク(CNN)で検証します。BatchNormがすごいとは言われているものの、具体的にどの程度精度が上昇するのか、あるいはどの程度計算速度とのトレードオフがあるのか知りたかったので実験してみました。
今回は隠れ層の数とBatch Normの有無、Batch Normの頻度ごとに誤差・精度を検証します。
Batch Normの簡単な理論
ニューラルネットワークの入力層(訓練データ)に対して標準化をすると訓練速度が向上しますが、これを隠れ層に対しても標準化するのがBatch Normです。
\begin{align}
\mu&=\frac{1}{m}\sum_i z^{(i)} \\
\sigma^2 &= \frac{1}{m}\sum_i (z^{(i)}-\mu)^2 \\
z_{\rm norm}^{(i)} &= \frac{z^{(i)}-\mu}{\sqrt{\sigma^2+\epsilon}} \\
\tilde{z}^{(i)} &= \gamma z_{\rm norm}^{(i)}+\beta
\end{align}
zがミニバッチなり訓練データに対する、活性化関数適用前の隠れ層の値とします。ここでの平均、分散を計算して、平均0、分散1になるようにシフトします。3つ目の式で微小な値εを足しているのは、0で割るのを避けるための技術的な理由です。βやγは学習からコントロールできますが、それぞれ平均、標準偏差に相当します。
実験
CPUで訓練できそうな軽いデータにしたかったのでFashion-MNISTにしました。MNISTも食傷気味なので。MNISTよりも若干難しいデータセットですが、CIFAR-10といったカラーのデータセットよりは全然簡単です。
- Fashion-MNISTを使った基本的な多クラス分類
- 畳み込み層だけの簡単なCNN(プーリングは使わない)。活性化関数は全てReLU
- 隠れ層を1~10に変えて、BatchNorm有無で、訓練誤差、訓練精度、テスト誤差、テスト精度、実行時間を比較(全20ケース)
- Conv2dの設定:フィルター数は層の番号×2で定義。例えば1番目の隠れ層ではフィルター数が2、2番目の隠れ層ではフィルター数は4……。カーネルサイズは全ての層で3とし、パディングはなし。したがって、1層ごとに縦横のサイズが2ずつ減って、チャンネル数が2ずつ増える。(26, 26, 2)→(24, 24, 4)→(22, 22, 6)→……
- 全結合以降は即softmaxを食わせて出力層とする
- BatchNormを入れる場合は、Conv2d→BatchNorm→Activation→Conv2d…の順で入れる
- 訓練は全てCPU
- どのモデルも20epoch訓練させる
- ドロップアウトは使わない
- オプティマイザはAdam、誤差関数はcategorical_crossentropy
- ハイパーパラメータは全てKerasのデフォルト設定。学習率も変えない。ミニバッチサイズは全て64とする。
- 訓練・テストの分割はKeras.datasets.fashion_mnistから読める分割
実験コード
前処理は255で割って0~1のスケールにしただけです。Fashion-MNISTの訓練データが(60000, 28, 28)の次元なのでCNNに食わせるために(60000, 28, 28, 1)に変形させています。
コード全体:https://gist.github.com/koshian2/de97a35e4e4f4860c86f90d0620fc76a
import numpy as np
import matplotlib.pyplot as plt
import pickle
import time
from keras.datasets import fashion_mnist
from keras.models import Model
from keras.layers import Input, Activation, Conv2D, BatchNormalization, Flatten, Dense
from keras.optimizers import Adam
from keras.utils import to_categorical
(X_train, y_train), (X_test, y_test) = fashion_mnist.load_data()
# 標準化
X_train, X_test = X_train / 255.0, X_test / 255.0
# ランク4にする
X_train, X_test = X_train[:, :, :, np.newaxis], X_test[:, :, :, np.newaxis]
# One-hotベクトル化
y_train, y_test = to_categorical(y_train), to_categorical(y_test)
モデルを作る根幹部分はこちら。use_bnのフラグを入れたときのみBatchNormを入れています。簡単に動的なモデルを作れるKerasすごいですね。
# モデルの作成
def create_model(nb_layers, use_bn, bn_freq=1):
# 入力層
input = Input(shape=(28, 28, 1))
x = input
# 隠れ層
for i in range(nb_layers):
x = Conv2D(filters=2*(i+1), kernel_size=(3, 3))(x)
if use_bn and ((i+1)%bn_freq==0):
x = BatchNormalization()(x)
x = Activation("relu")(x)
# FC
x = Flatten()(x)
# 出力層
y = Dense(10, activation="softmax")(x)
# モデル
model = Model(inputs=input, outputs=y)
return model
bn_freqでBatchNormを入れる間隔を指定できますが、ここでは1(全ての層に対して入れる)ものとします。後でこの値を変更して別に実験します。次に実験本体部分です。隠れ層1+BNなし→隠れ層1+BNあり→隠れ層2+BNなし→隠れ層2+BNあり→…の順でテストしていきます。
# 定数
nb_epoch = 20
# 結果の保存用
result = []
times = []
# レイヤー数10、BN有りなしの計20
for i in range(20):
nb_layers = int(i/2) + 1
use_bn = i % 2 == 1
print(f"★★ i = {i}, #layers = {nb_layers}, bn = {use_bn} ★★")
# モデルの取得
model = create_model(nb_layers, use_bn)
# コンパイル
model.compile(optimizer=Adam(), loss="categorical_crossentropy", metrics=["accuracy"])
# フィット
start_time = time.time()
history = model.fit(X_train, y_train, batch_size=64,
epochs=nb_epoch, validation_data=(X_test, y_test)).history
elapsed = time.time() - start_time
# 結果に追加
result.append(history)
times.append(elapsed)
# 保存
with open("result.dat", "wb") as fp:
pickle.dump(result, fp)
with open("times.dat", "wb") as fp:
pickle.dump(times, fp)
Pickleでhistoryをファイルに保存して終わりです。
結果
処理時間
BatchNorm有無での訓練時間の推移は次のようになります。
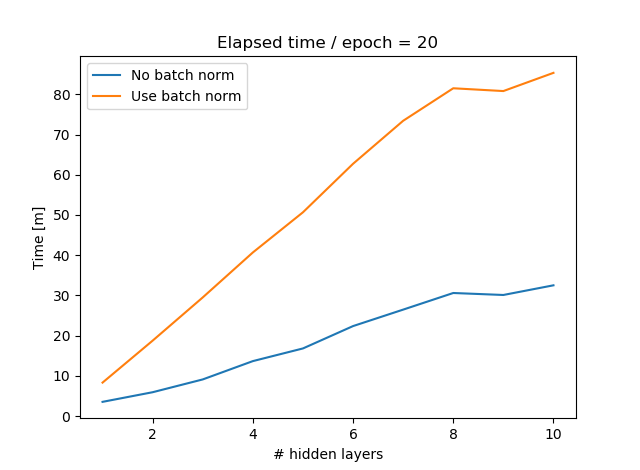
これは全ての層でBatchNormを入れた場合です。GPUで訓練したり、データがカラーになるとまた変わるかもしれませんが、CPUでFashion-MNISTを訓練した限りでは、BatchNormが入るとほぼ処理時間は2.5倍~3倍になりました。
誤差、精度
BatchNorm有無での訓練/テストの誤差/精度は次のようになります。左上が訓練誤差、右上が訓練精度、左下がテスト誤差、右下がテスト精度です。横軸はepoch数、縦軸が評価尺度です。
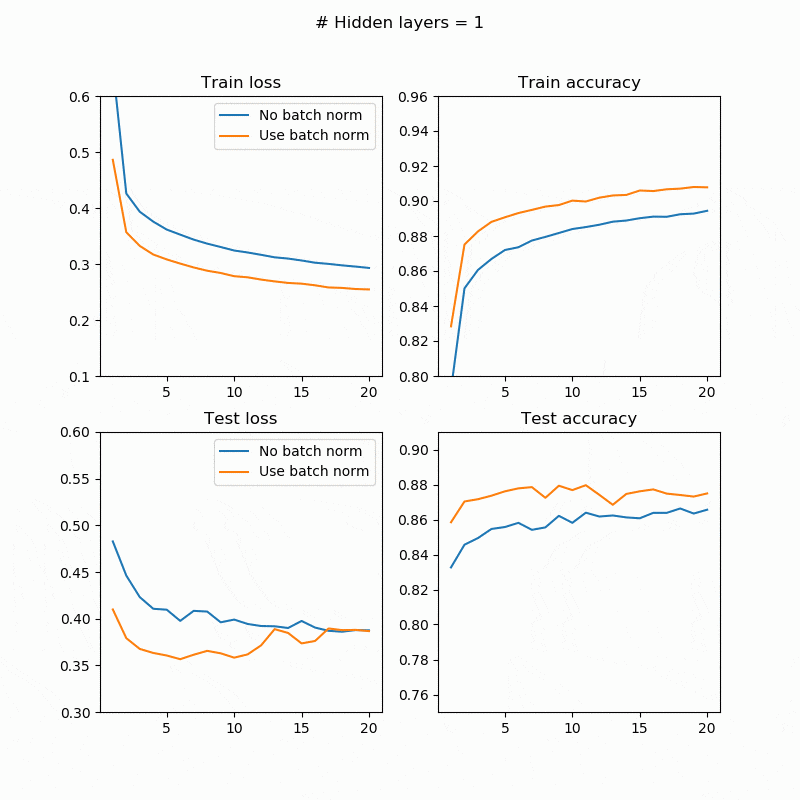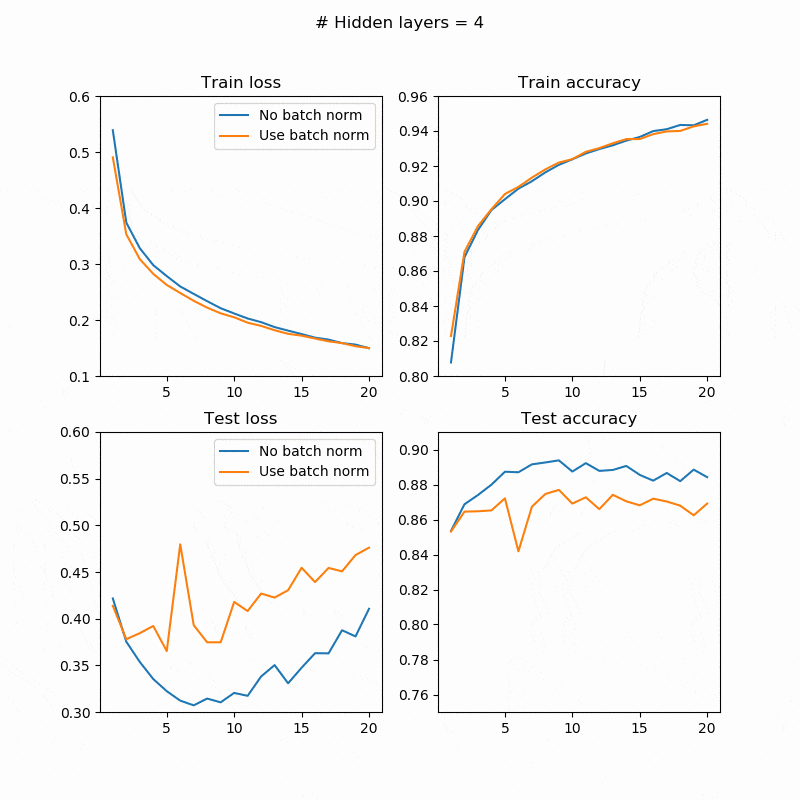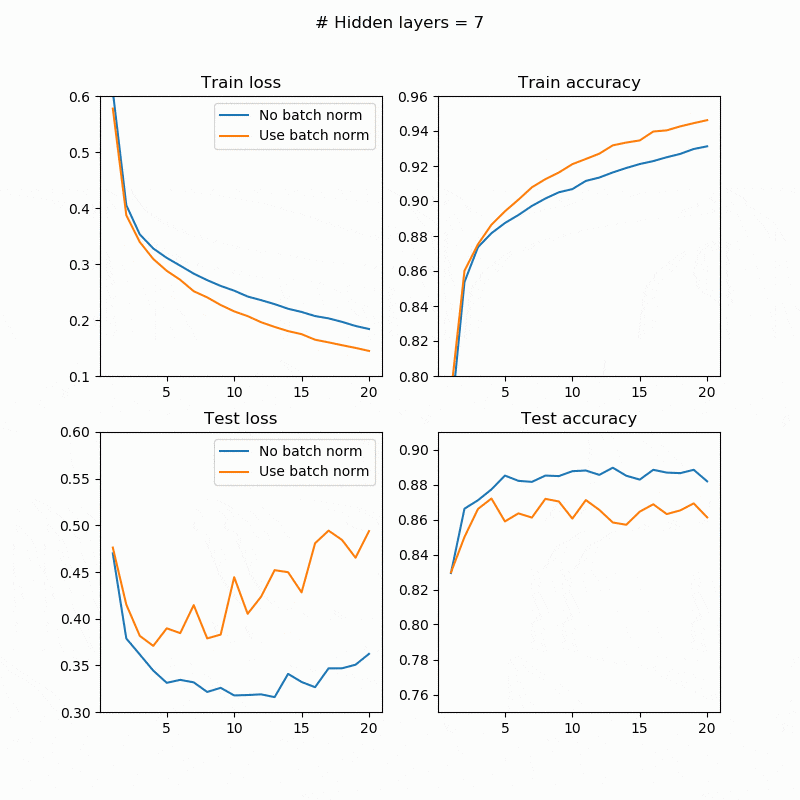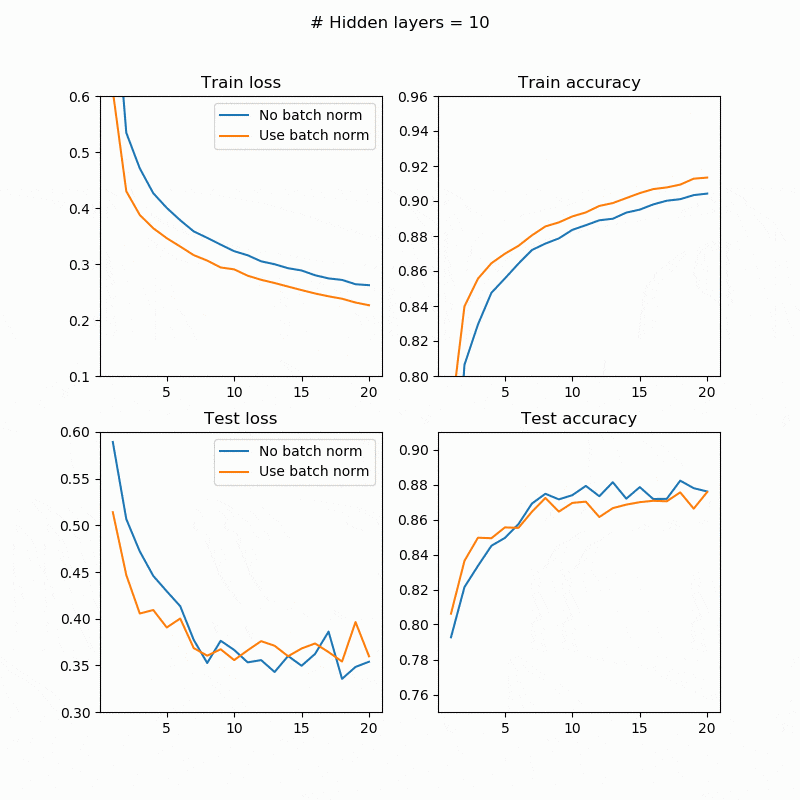
テストの場合はまちまちですが、訓練では必ずBatchNorm入れたほうが精度が良くなっている(誤差が小さくなっている)のが確認できます。BatchNormの有無に関わらず訓練誤差を下げても、テスト誤差は同じように下がる保証はありません(オーバーフィットしているかどうかの問題なので)。隠れ層の数が大きくなると精度が下がっていますが、おそらく20epoch程度では足りなかったのだと思います。もう少し長く訓練させたらちゃんと精度が上がるはずです。
必ず訓練誤差が下がるのはすごいことです。ニューラルネットワークの収束を速くするテクニックは数多くあれど、このようにほぼ必ず効果があるテクニックはかなり限られます。
ただ問題は時間とのトレードオフでしょう。計算資源が潤沢にあり、「BatchNormの計算時間ぐらい気にならないや」というのであれば全部入れてしまえばいいのですが、先程見たように全部入れると2.5倍~3倍になります。例えば隠れ層が2のときに、BatchNormありで5epochのときの精度≒BatchNormなしの10~15epochのときの精度なので、計算量が3倍程度になれど、BatchNormを入れるのはかなり合理的なように考えられます。
もちろんBatchNormを入れる頻度はハイパーパラメータなので、データやモデル、計算環境に合わせて調整するといいと思います。次はBatchNormの頻度を変えて実験してみます。
追加実験
- 隠れ層の数は6とする(そこそこに数が大きくてBatchNormの有効性の差が出たのがここだったので)。
- BatchNormの頻度を1~7に変更して同様に見る。1は全ての隠れ層に対して、7は一切BatchNormを入れない場合。
- その他の条件は前の実験と一緒
実装
一部だけ。全体はこちらを見てください。
# レイヤー数6、BN有りの計7
for i in range(7):
print(f"★★ i = {i}★★")
# モデルの取得
model = create_model(6, True, i+1)
# コンパイル
model.compile(optimizer=Adam(), loss="categorical_crossentropy", metrics=["accuracy"])
# フィット
start_time = time.time()
history = model.fit(X_train, y_train, batch_size=64,
epochs=nb_epoch, validation_data=(X_test, y_test)).history
elapsed = time.time() - start_time
# 結果に追加
result.append(history)
times.append(elapsed)
結果
時間
bn_freqを横軸に、時間(分)を縦軸にプロットしました。bn_freq=1では全てのレイヤーでBNあり、bn_freq=2では2層ごと、……、bn_freq=7ではBNなしとなります。この場合、BatchNormの頻度と処理時間は直線的には変化しませんでした。なぜならbn_freq=1では6回、bn_freq=2では3回、bn_freq=3では2回、bn_freq=4では1回入れていてあとは入れる層が異なるだけだからです。BatchNormの回数で見ると、処理時間は直線的な関係がありそうです。
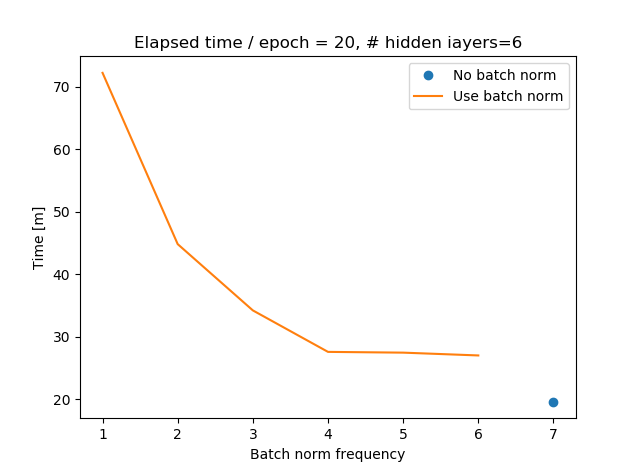
この例だと、BNありで処理時間1.4倍ぐらいですんでいるbn_freq=4あたりがコストパフォーマンス良さそうですね。もちろんこれは隠れ層の数や、学習率、データ、CPUやGPUかによって変わるので絶対ではありません。
誤差、精度
1回でもBatchNorm入れれば結構上がりますね。bn_freq=2、4あたりがいい感じです。全てのレイヤーに対してBatchNormを入れる必要はこの場合はなさそうです。
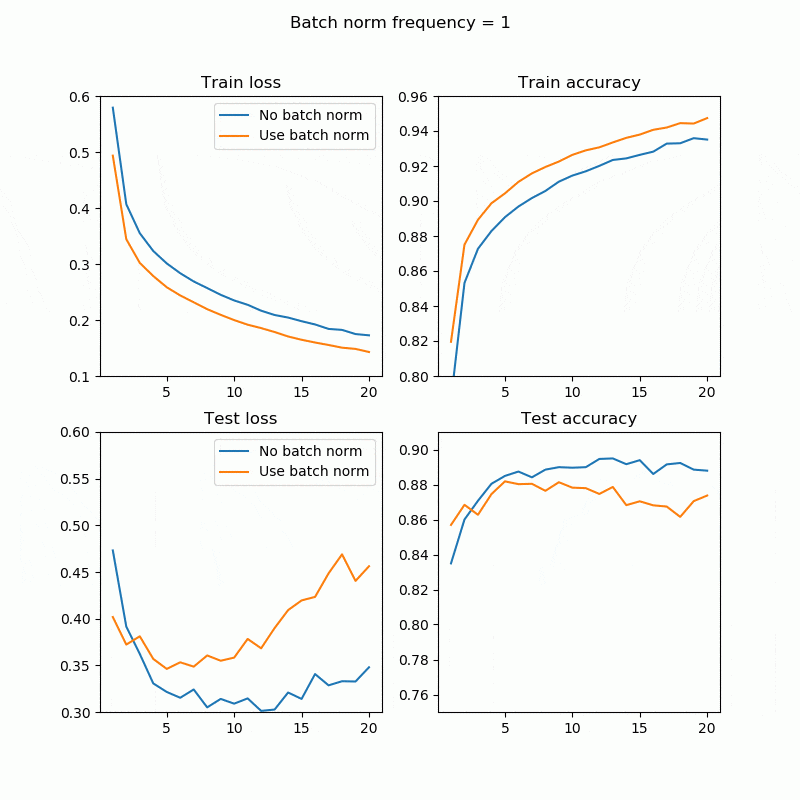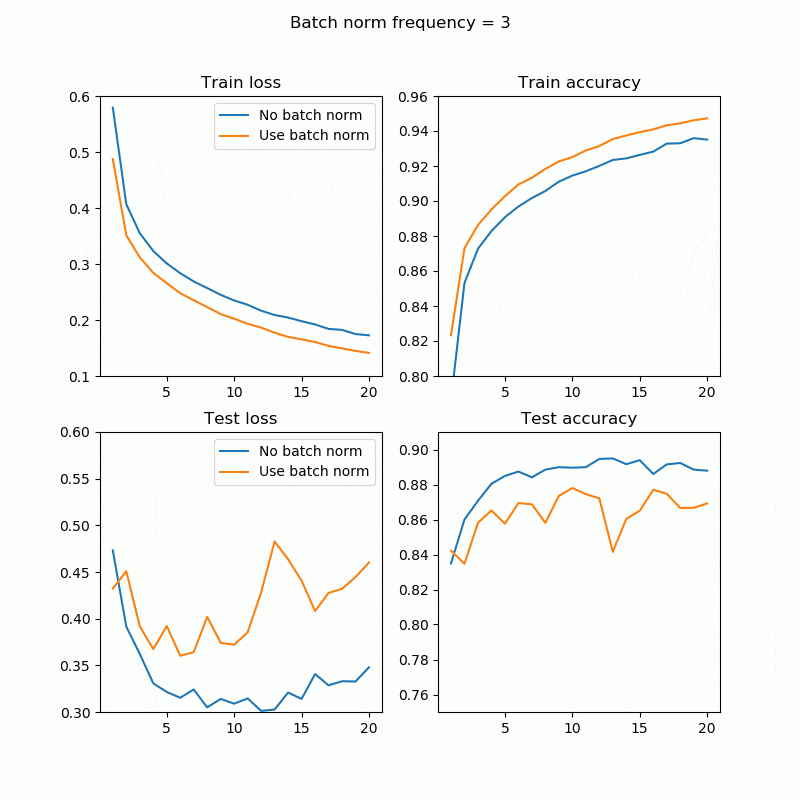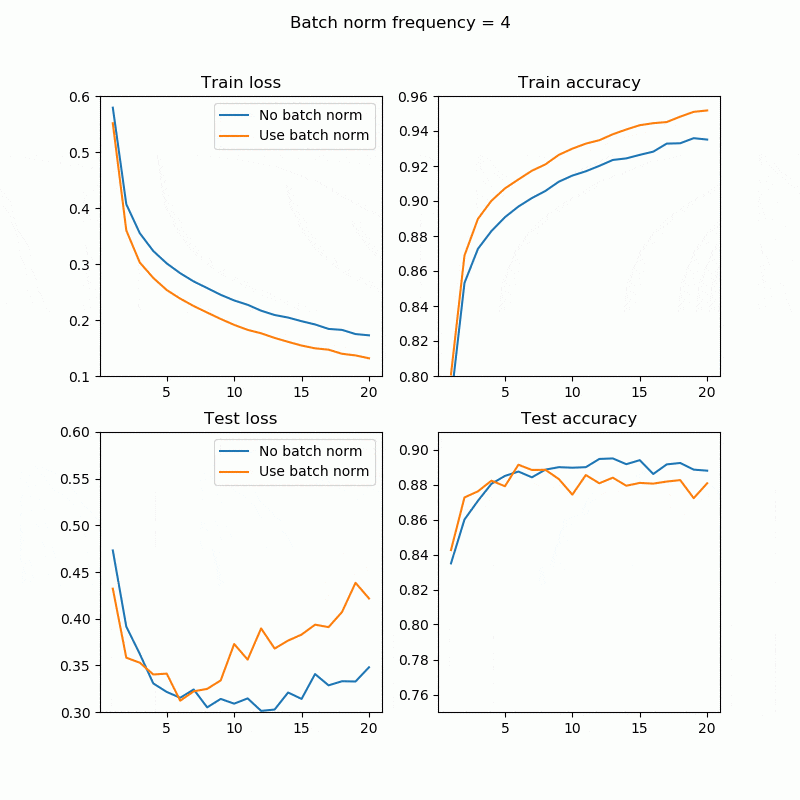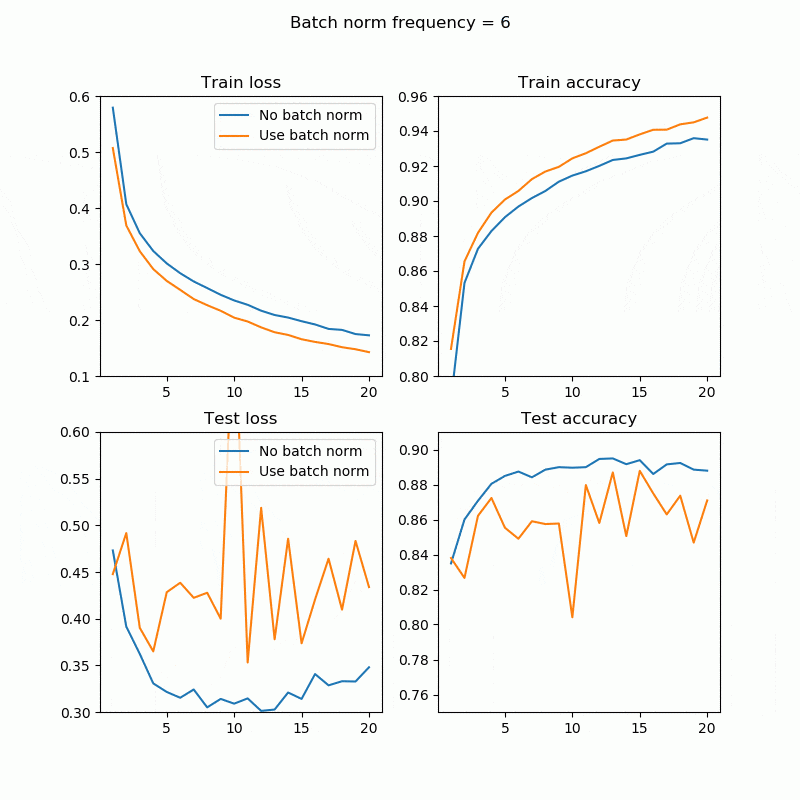
まとめ
BatchNorm強い。Fashion-MNIST+Adamだと訓練精度基準で、epoch数でせいぜい2倍程度の加速でしたが、CIFAR-10+SGDだともっと(5倍や10倍)加速したという例もあります。