はじめに
前回、こういう記事をかきました ![]()
Deep LearningにおけるDropoutの理解メモと、実際にどう効いているのか見てみる
引き続き https://deeplearningbook.org を読んでおり、上記記事でも少し紹介したBatch Normalizationが8章で出てきました。
Dropoutの節では、「Batch Normalizationが超強いからDropoutいらないこともあるよ」とまで言われるレベルのパワーとのこと。一体どんなものなのか ![]()
本記事では自身の学習のアウトプットとして、簡単な理解のまとめと、TensorFlowでの実装の説明、cifar10のデータセットにBatch Normalizationあり/なしのCNNで分類を行ったので、その結果を載せています。
- Batch Normalizationの理解
- TensorFlowでの実装
- cifar10で実験
- まとめ
勉強中ゆえ、変な表現や間違いあればご指摘歓迎です ![]()
Batch Normalizationの理解
概要
Batch Normalizationは、Deep Learningにおける各重みパラメータを上手くreparametrizationすることで、ネットワークを最適化するための方法の一つです。近年のイノベーションの中でもかなりアツい手法だと紹介されています。
2015年にIoffe and Szegedyによって発表されました。
基本的には、各ユニットの出力をminibatchごとにnormalizeした新たな値で置き直すことで、内部の変数の分布(内部共変量シフト)が大きく変わるのを防ぎ、学習が早くなる、過学習が抑えられるなどの効果が得られます。
その効果はかなり大きく、前述の通りDropoutがいらなくなると言われるレベルとのことです。
内部共変量シフト
共変量シフトというのは、こちらで書かれている通り、データの分布が訓練時と推定時で異なるような状態のことを言います。
訓練中にネットワーク内の各層の間で起きる共変量シフトを内部共変量シフトと言うようです。
Deep Learningのトレーニングでは、入力データを基にモデルの出力を計算し、誤差関数を計算し、誤差を各層にback propagationしていくことで各パラメータの勾配を求め、パラメータを更新します。
モデルの中では、各層がその時受け取った入力を基に出力を計算しています。
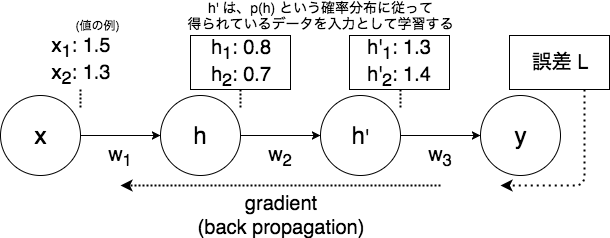
(画像1: 3層で単一のユニットを持つようなネットワークと、伝播する値のイメージ)
ここで、すべてのパラメータの更新は同時に行われますが、あるパラメータを更新する際は他の層は固定して考えます。すると、更新後のある層についての入力の分布が、更新前とは変わる場合があります。
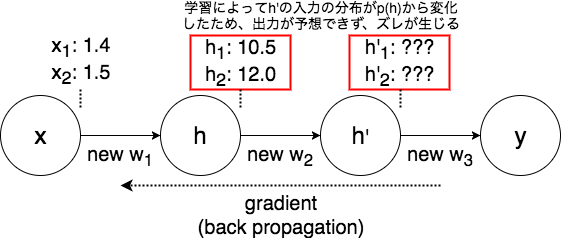
(画像2: パラメータ更新によってh'の入力の分布が変化するイメージ)
この層では、1ステップ前までの入力を基に学習していたため、新たな分布の入力に対して良い出力値を返すことが難しくなります。
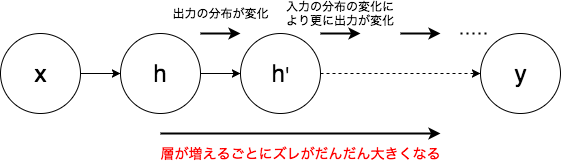
画像は少し極端な例ですが、ネットワークがDeepになればなるほどこのズレが広がっていき、結果として出力層に近い層の学習に時間がかかってしまいます。
(画像3: deepなイメージ)
Batch Normalization
ネットワークのある層毎に、$\boldsymbol{H}$という行列を定義します。これは、各行がminibatchの1つのデータ、各列がそれぞれのactivationとなるような値をとる行列です。
batch sizeが128, hidden unitの数を256とすると、 $\boldsymbol{H}$ は128×256の行列になります。
これを正規化するために、次のように $\boldsymbol{H}'$ と置き直すのがbatch normalizationです。
\boldsymbol{H}' = \frac{\boldsymbol{H}-\boldsymbol{\mu}}{\boldsymbol{\sigma}},
ここで、$\boldsymbol{\mu}$と$\boldsymbol{\sigma}$ は、その層での各ユニットの平均、及び標準偏差のベクトルを表しています。
上記の式は行列とベクトルの演算になってしまっていますが、 $\boldsymbol{H}$ の各行にそれぞれのベクトルかかるようにbroadcastingしています。
即ち、 $H_{i,j}$ の正規化は、 $\mu_j$, $\sigma_j$ を使って計算されます。
トレーニング時の $\boldsymbol{\mu}$ , $\boldsymbol{\sigma}$ は次で与えられます。
\boldsymbol{\mu} = \frac{1}{m} \sum_i \boldsymbol{H}_{i,:}, \\
\boldsymbol{\sigma} = \sqrt{\delta + \frac{1}{m} \sum_{i}(\boldsymbol{H}-\boldsymbol{\mu})^2_i}
$\delta$ は、標準偏差が0になってしまうのを防ぐ、$10^{-8}$のような小さな値です。
推定時は、minibatchなどはないため、$\boldsymbol{\mu}$ , $\boldsymbol{\sigma}$ は訓練中に計算したものの移動平均を使います。
ネットワークに入れて計算するとなると少しややこしいですが、考え方自体は非常に単純ですね!
過去には、他のアプローチもあったようです。
- 正則化項を入れて、パラメータが上手く正規化されるようにする
- 勾配降下法の1ステップごとに間に入って、各ユニットの統計量をnormalizeする
前者はそもそもあまり効果が出ず、後者は時間がかかりすぎてしまいます。
batch normalizationはこれらの課題をうまく回避できているとのことでした。
その他の話
表現力のカスタマイズ
各ユニットをnormalizeすることは、各ユニットの表現力を減らすことにもなります。
そこで、ユニットの表現力を維持するために、元の $\boldsymbol{H}$ の代わりにnormalize後の $\boldsymbol{H}'$ をそのまま使うのではなく、 $\boldsymbol{\gamma H}' + \boldsymbol{\beta}$ を使うというアイディアがあります。
$\boldsymbol{\gamma}, \boldsymbol{\beta}$は、新しいパラメータに任意の平均や標準偏差を与えるためのパラメータです。
せっかく batch normalization を使って平均を0にしたのに、また $\boldsymbol{\beta}$ を足して平均値を与えるという、この「消して戻す」みたいな処理には意味があるんだろうか? ![]() と思ってしまいましたが、deeplearningbookによると、「learning dynamicsが異なるため、学習しやすくなる」とのことでした。
と思ってしまいましたが、deeplearningbookによると、「learning dynamicsが異なるため、学習しやすくなる」とのことでした。
元の $\boldsymbol{H}$ において、平均は、下の層の様々な相互作用の上で計算することになりますが、新しいパラメータでの $\boldsymbol{\gamma H}' + \boldsymbol{\beta}$ での平均は単純に $\boldsymbol{\beta}$ を見れば良いからとのこと。
直感的な理解は難しそうですが、一度正規化してから平均を新たに与えてやることで、どのような出力になるのかは確かにわかりやすくはなりそうです。
どのタイミングでbatch normalizationを適用するか
多くのニューラルネットワークの層は、SigmoidやReLUなどのactivation function $\phi$ を使って、 $\phi(\boldsymbol{XW}+\boldsymbol{b})$ で表すことができます。
では、どのタイミングでBatch Normalizationを入れれば良いでしょうか。$\boldsymbol{X}$自体なのか、変換後の値 $\boldsymbol{WX}+\boldsymbol{b}$ なのか。
元論文では、後者の $\boldsymbol{WX}+\boldsymbol{b}$, 正確には、バイアスは正規化処理で消えるため、 $\boldsymbol{WX}$ にあてることが推奨されています。
TensorFlowでの実装
コードは github においてますので、詳しくはそちらを見てください。
環境はPython 3.6.2, TensorFlow 1.8.0です。
ここでは、メインのモデル部分のコードを載せます。
# モデル
class CNN:
__slots__ = ['x', 'y', 'y_onehot', 'is_training', 'logits', 'predicted_classes']
def __init__(self, config):
shape_x = np.array([None, 32, 32, 3])
shape_y = np.array([None]) # not one-hot vector
self.x = tf.placeholder(dtype=myfloat, shape=shape_x, name='x')
self.y = tf.placeholder(dtype=myint, shape=shape_y, name='y')
self.y_onehot = tf.one_hot(indices=tf.cast(self.y, myint), depth=10)
self.is_training = tf.placeholder(dtype=bool, name='is_training')
l_1 = tf.layers.conv2d(inputs=self.x,
filters=32,
kernel_size=[5, 5],
padding='same',
activation=tf.nn.relu)
if config['is_use_bn_conv']:
l_1 = tf.layers.batch_normalization(l_1, training=self.is_training)
l_2 = tf.layers.max_pooling2d(inputs=l_1, pool_size=[2, 2], strides=2)
l_3 = tf.layers.conv2d(inputs=l_2,
filters=64,
kernel_size=[5, 5],
padding='same',
activation=tf.nn.relu)
if config['is_use_bn_conv']:
l_3 = tf.layers.batch_normalization(l_3, training=self.is_training)
l_4 = tf.layers.max_pooling2d(inputs=l_3, pool_size=[2, 2], strides=2)
l_4_flat = tf.reshape(l_4, [-1, 4096])
l_5 = tf.layers.dense(inputs=l_4_flat, units=1024, activation=tf.nn.relu)
if config['is_use_bn_dense']:
l_5 = tf.layers.batch_normalization(l_5, training=self.is_training)
if config['is_use_dropout']:
l_5 = tf.layers.dropout(inputs=l_5,
rate=config['dropout_rate'],
training=self.is_training)
l_6 = tf.layers.dense(inputs=l_5, units=10)
self.logits = l_6
self.predicted_classes = tf.argmax(input=self.logits, axis=1, output_type=myint)
ネットワークはTensorFlowのチュートリアルを参考にしたCNNになっています。
入力の次元が異なること以外は基本同じです。
configというdictを渡してdropoutやbatch normalizationを切り替えています。また、is_trainingというplaceholderを用意して、訓練時とテスト時を分けています。
主題のBatch Normalizationですが、コードにある通り、 tf.layers.batch_normalization を使うことで簡単に実装できます。
中ではtf.nn.batch_normalizationを呼んでおり、そちらを直接使うのもアリですが、移動平均を計算したりとやることが結構増えて大変なので特殊なことをしたいわけでなければ tf.layers.batch_normalization を使えば良いと思います。
また、上記メソッドの公式説明にもありますが、訓練時に少しコードを足さないとテスト時にうまく回らなくなります。
# トレーニング
crossent = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=self.cnn.y, logits=self.cnn.logits)
loss_op = tf.reduce_mean(crossent)
optimizer = tf.train.AdamOptimizer(config['learning_rate'])
extra_update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS) # <- ここ
with tf.control_dependencies(extra_update_ops): # <- ここ
train_op = optimizer.minimize(loss_op)
Batch Normalizationは前述の通り、テスト時は移動平均・移動分散を使用していますが、そのままトレーニングするだけではこれらが更新されません。
そのため、このままだとテスト時に移動平均の初期値(1など)を使ってnormalizeされてしまうことになり、うまく推定できなくなります。
これを回避するために、 extra_update_ops の部分を足す必要があります。
dependenciesを使って書いていますが、明示的に sess.run(extra_update_ops) のように計算するようにしても問題ないはずです。
cifar10での実験
次のような条件のパターンで、cifar10を用いて実験を行いました。ネットワークは上記のものです。
| ID | Dropout | Batch Normalization |
|---|---|---|
| 0 | なし | なし |
| 1 | 0.2 | なし |
| 2 | 0.4 | なし |
| 3 | なし | convolution層 |
| 4 | 0.2 | convolution層 |
| 5 | 0.4 | convolution層 |
| 6 | なし | dense層 |
| 7 | 0.2 | dense層 |
| 8 | 0.4 | dense層 |
| 9 | なし | convolution層, dense層 |
| 10 | 0.2 | convolution層, dense層 |
| 11 | 0.4 | convolution層, dense層 |
また、グラフのy軸はcifar10のTestデータでのaccuracyで、[0.4, 0.8]の範囲を取っています。
Batch Normalizationがない場合
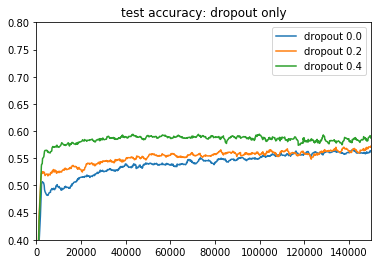
前回Dropoutの記事を書きましたが、実験がシンプルなDNN×mnistによるものだったので、今回のCNN×cifar10の場合でDropout有無でどう変わるのかをまずは見てみます。
0,1,2のケースに当たります。
前回よりもdropoutの効果がわかりやすく出たかな ![]()
CNNのdense層でのdropoutは結構有効みたいですね。
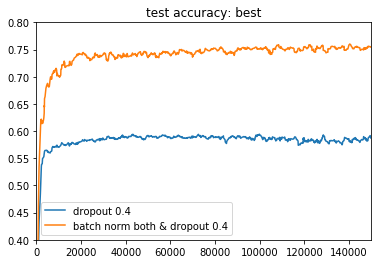
BestケースとそのBatch Normalization無しケースでの比較
今回一番結果が良かったのは11の、convolution層とdense層の両方にbatch normalizationを入れて、dropoutを確率0.4で入れたもの(全部入り)でした。
それを、dropout同条件のbatch normなしとプロットしました。
batch normalizationなしではTest Accuracyが0.6以下だったのに、有りでは0.75に届くレベルになっています...!かなり強力ですね ![]()
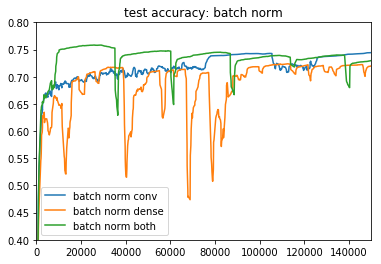
Batch Normalizationの比較(convolution層,dense層,両方)
Dropoutなし
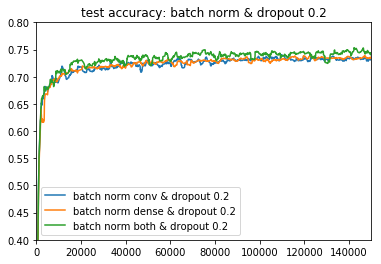
Dropout 0.2
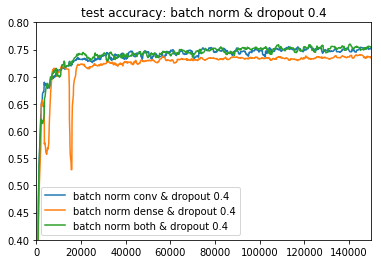
Dropout 0.4
Dropoutがなかったり、batch normがdense層だけだったりすると、モデルがやや不安定になる傾向が見えます。どっちも入れている緑のラインが一番良いですね。
deeplearningbookでは、「Batch NormalizationがあればDropoutがいらないことも」と書かれていましたが、今回の場合は両方あったほうが良いですね ![]()
まとめ
- Batch Normalizationは、重みパラメータをminibatchごとに正規化することで最適化の効率を上げる手法
- 今回のネットワークでは...
- Batch NormalizationはDropoutよりも確かに強力
- convolution層、dense層ともに入れたほうが安定する
- とはいえDropoutも一緒に入れたほうが安定するので良さそう
また、Batch Normalizationよりも新しい手法として、Layer Normalizationなるものもあるらしいです。
次はそれを見てみたいと思います ![]()