はじめに
https://deeplearningbook.org を読んでDeepLearningを勉強していて、7部でDropoutが出てきました。
Dropoutの章を読む前の理解は、こんな感じでした。
- Dropout、名前は聞いたことある
- 確か一部のユニットを消すことで性能があがるとかなんとか
- なんで効果があるのかはよく分からん
本記事では、自身の学習のアウトプットとして、簡単な理解のまとめと、実際に効果があるのかmnistのデータセットで確認したのでその結果を載せています。
- Dropoutの理解
- mnistで実験
- まとめ
勉強中ゆえ、変な表現や間違いあればご指摘歓迎です ![]()
Dropout の理解
簡単にまとめると、Dropoutは次のようなものです。
- 汎化性能を上げるための手法の一種
- 確率的に一部のユニットをなかったことにしてforward, backwardを計算する
- Baggingのような理解ができる
- いくつかの近似のもと、Baggingとは違ってデータ量や計算量はそこまで大きく増えない
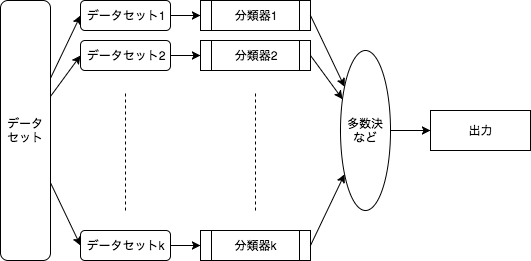
Bagging?
ある分類問題について、複数の弱学習器に異なるデータセットで学習させ、多数決的に出力を決めることで汎化性能を上げる手法です。
バギングを使うことで、誤差のバリアンスによるところを減らすことが証明されています。
詳しくは他の解説記事を読んで下さい。(丸投げ![]() )
)
DropoutにおけるBagging的解釈
Dropoutで上記のようなBaggingを実現することを考えます。
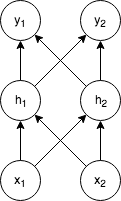
次のような単純なネットワークがあるとします。
Dropoutを使うことで、計算の際に確率的に一部のユニットを消すことになります。即ち、上記のネットワークに対して、次のような多くのサブネットワークができることになります。
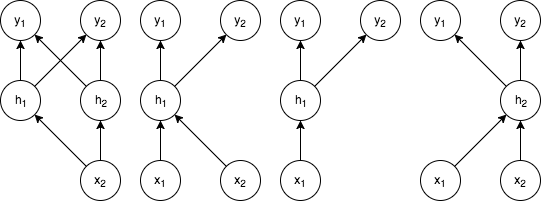
図2: 図1の一部ユニットを消すことでできるサブネットワークの例
この、元のネットワークについて一部のユニットを消すことで与えられるサブネットワークの集合を、Baggingの弱分類機として扱うことで汎化性能を上げる、というのがDropoutの考え方です。
ところが、単純にBaggingをやると、計算量が大変なことになるため、上手くやるための工夫がいくつかあります。次にそれをBaggingとの違いとして紹介します。
訓練時のBaggingとの違い
Baggingでは、次のようなステップで学習します。
- k個の異なるモデルを用意する
- データセットからk個のサブデータセットを用意する(ブートストラップサンプリングなど)
- i番目のモデルをi番目のデータセットで学習する
Dropoutでは、このプロセスを近似的に行います。
まず(1)のモデル数については、上述の確率的にユニットを消すという作業によって、簡単に指数関数的に多くのサブネットワークを作成することが出来ます。
次に(2), (3)について。Deep Learningでは学習時にデータをminibatchに分割して学習しますが、その際に、ハイパーパラメータとして与えられる確率によって、ユニット数分のバイナリのマスクとなるベクトル $\mu$ を作成します。
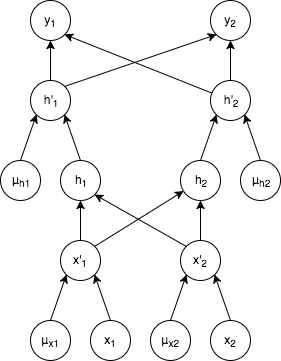
各ユニットに対応するマスクベクトルの値が1であればユニットは残し、0であれば消す、という処理を行います。先程のネットワークにマスクベクトル $\mu$ を加えたもののイメージが下記になります。
これによって、次のような違いが発生します。
- Baggingでは各モデルは独立だが、Dropoutでは各モデルはパラメータを共有する
- Baggingでは各モデルがそれぞれのデータに対して収束するまで学習するが、Dropoutでは多くのモデルは十分にはトレーニングされない。
各モデルについて十分にトレーニングするためには、多くの時間とデータが必要になります。基本的には各モデルを1度のステップだけで学習し、その分を、各パラメータを共有して補うことで、全体として良い値となるそうです。
(ここがどの程度上手く学習できるのかどうかは気になるところです、もし関連研究があれば教えてください。)
これ以外は特にBaggingと変わらないとの説明がされていました。
推論時のBaggingとの違い
Baggingのようなアンサンブル学習では、推論時は次のように確率分布の平均を取り、最も確率の高いクラス$y$を選択することになります。
\frac{1}{k} \sum_{i-1}^{k} p^{(i)}(y | \boldsymbol{x})
Dropoutでは、確率的に生成されるマスクベクトル $\mu$ の確率分布である $p(\boldsymbol{\mu})$ を用いて、次のように期待値を取ることで確率を計算します。
\sum_{\boldsymbol{\mu}}p(\boldsymbol{\mu})p(y|\boldsymbol{x}, \boldsymbol{\mu})
ところが、上記の $\boldsymbol{\mu}$ についての和は、2のユニット数乗の和になるため、通常のネットワークでは計算が非常に難しくなります。
ここで、Dropoutではweight scaling inference ruleと呼ばれる近似アプローチを用いることで、上記の和をたった1回の計算で置き換えます。
やることはものすごく単純で、各ユニットからの出力にかかる重みに、それぞれのユニットをdropoutで消す確率 $p(\boldsymbol{\mu})$ を書けたものを新たな重みとするだけです。
例えば、ハイパーパラメーターとしてDropoutの確率を0.5と与えていた場合、最終的に得られたモデルの重みに0.5をかけたものを推論時に使用します。
この近似は、例えば非線形性のないネットワークについては厳密で、その他の多くの非線形性を持つネットワークについてはまだ理論的に解析されていませんが、経験的にうまくいくことが報告されているそうです。
(と、deeplearningbookには書かれていたけど、今だと何か研究が進んでいたりするかもしれません。)
実験
なんとなく理屈は分かったけど、本当にそんな近似で上手くいくのかな、と思い簡単な設定でTensorflowを使って試しました。
Tensorflowには
tf.nn.dropout https://www.tensorflow.org/api_docs/python/tf/nn/dropout
tf.layers.dropout https://www.tensorflow.org/api_docs/python/tf/layers/dropout
などあるので簡単に実装できます。
# 例: layerで定義したtensorflowのlayerをdropout可にする
layer = tf.layers.dropout(layer, rate=dropout_rate , training=is_training, name='sample_dropout')
設定
データセットにmnistを用いて、単純なDNNで分類を行うことを考えます。
下記のような条件で比較してみました。
| id | 中間層の数 | 各層のユニットの数 | dropoutの有無 |
|---|---|---|---|
| a | 2 | 128 | なし |
| b | 2 | 128 | あり |
| c | 2 | 1024 | なし |
| d | 2 | 1024 | あり |
| e | 4 | 128 | なし |
| f | 4 | 128 | あり |
| g | 4 | 512 | なし |
| h | 4 | 512 | あり |
| i | 8 | 128 | なし |
| j | 8 | 128 | あり |
| k | 8 | 256 | なし |
| l | 8 | 256 | あり |
中間層のactivation functionにはreluを使っており、dropout の rateはlayer数2のときは入力には0.2, 中間層には0.4を指定し、中間層が4のときは0.1及び0.2、8のときは0.05及び0.1という風に減らしています。
これは、レイヤー数が多いときに学習が上手く行かなくなったためです。
また、どのネットワークもある程度training errorが収束するまでは回しました。
結果
先に最終的なtrainingデータとtestデータに対するaccuracyと、その差を下記に示しました。
その次に、それぞれでトレーニングデータ数毎のaccuracyの変化についてグラフで見てみます。
表: 各ネットワークの test accuracy の一覧
| id | network | test accuracy |
|---|---|---|
| a | 2層, 128, dropoutなし | 0.981 |
| b | 2層, 128, dropoutあり | 0.979 |
| c | 2層, 1024, dropoutなし | 0.980 |
| d | 2層, 1024, dropoutあり | 0.982 |
| e | 4層, 128, dropoutなし | 0.981 |
| f | 4層, 128, dropoutあり | 0.979 |
| g | 4層, 256, dropoutなし | 0.981 |
| h | 4層, 256, dropoutあり | 0.984 |
| i | 8層, 128, dropoutなし | 0.980 |
| j | 8層, 128, dropoutあり | 0.981 |
| k | 8層, 256, dropoutなし | 0.978 |
| l | 8層, 256, dropoutあり | 0.981 |
見て分かる通り、ネットワークによってそこまで大きな変化はありません。
これは単に、どのネットワークでもある程度誤差が収束するまで訓練したのと、mnistが単純なタスクであるため、どのネットワークでもそこそこの性能が出るからです。
ちなみに、これ以上複雑なネットワークにすると上手く学習できないケースが増えました。
トレーニングデータ数による test accuracy の変化
最終的なaccuracyではどれも十分トレーニングしているため大きな差はでませんでしたが、データ数でのプロットを見るとdropoutの効果がわかります。
なお、見やすくするために、データはTensorboardからダウンロードしたもの(サンプリング数1,000)から、移動平均(幅10)を取ってプロットいます。縦軸はかなり拡大しており、グラフによって目盛りも異なりますのでご注意ください。
ここでは特に一部のグラフについて載せます。他のグラフはgithubにjupyter notebookを上げているのでそちらをご覧ください。
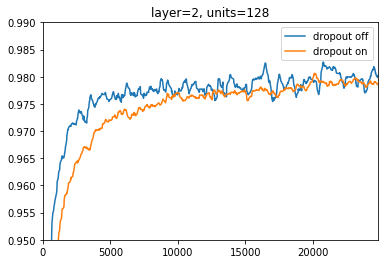
2層、ユニット128個の場合
おそらくシンプルなタスクに対して単純なネットワークだったため、特に大きな差は出ず、dropout有り時に訓練に時間がかかる部分が分かりやすい結果になりました。
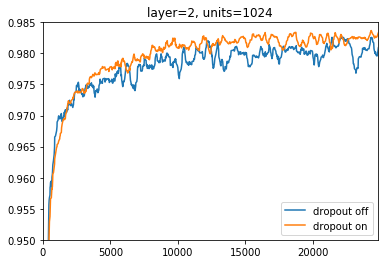
2層、ユニット1024個の場合
先程の場合と比べるため、ユニット数を増やして訓練に時間がかかるようにしたところ、先程の例とは対象的にdropoutの効果が分かる結果になりました。
dropoutなしに比べて、有りの方はaccuracyが高く、かつ安定していることがわかります。
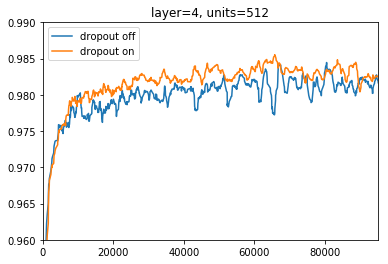
4層、ユニット512個の場合
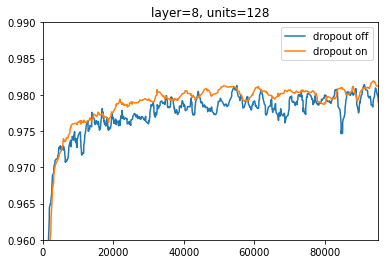
8層、ユニット128個の場合
4層、8層の場合でも似たような結果になりました。
accuracyが上がっているだけではなく、dropoutなしの場合に比べて大きな上昇や下降が減っているのがわかります。
また、ここでは紹介しませんが他にもいくつか試しました。単純に突っ込めば突っ込むほどうまくいくわけではないですね。
- 4層や8層など深いネットワークのときもdropoutの確率を0.4など大きめの値で訓練させると、上手く行きませんでした。
- 8層でユニット数1024個などでは初期値依存性が高くそもそも学習が上手く行かず、これにdropoutを加えても結果は変わりませんでした。
まとめ
- DropoutはDeep Learningにおいて汎化性能を上げるための手法の一つ
- Baggingと見ることが出来るが、計算量はBaggingと比べて非常に少ないまま多数の分類器を学習できる
- 何にでもうまくいくわけではなく、ハイパーパラメータ調整は必要
- あくまで汎化手法であり、元々簡単すぎるタスク・難しすぎるタスクの解決にはならない
他のグラフなど含めて、今回使用したnotebookはgithubにおいたので、間違いなどありましたらご指摘いただけると幸いです。 ![]()
次は Batch Normalizationをば!