2021年のディープラーニング論文を1人で読むAdvent Calendar24日目の記事です。今日読むのは「超解像技術」の論文です。
この論文はESRGANという、2018年の論文のリファインなのですが、訓練時の低解像度データの作成方法(訓練時の前処理)を大きく変えて、モデルはそれほど変わっていないという面白い改善です。通常この手のリファインはモデル構造側を工夫することが多いのですが、「前処理を実際の画像劣化に合わせることで、現場で通用するような超解像モデルを作りましょうね」というのがコンセプトです。前処理を変えるとこんなに変わるというのをぜひ体感してほしいです。
ICCV2021のWorkshopに採択されています。著者の所属は主にテンセントと中国科学院です。
- タイトル:Real-ESRGAN: Training Real-World Blind Super-Resolution With Pure Synthetic Data
- URL:https://openaccess.thecvf.com/content/ICCV2021W/AIM/html/Wang_Real-ESRGAN_Training_Real-World_Blind_Super-Resolution_With_Pure_Synthetic_Data_ICCVW_2021_paper.html
- 出典:Xintao Wang, Liangbin Xie, Chao Dong, Ying Shan; Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) Workshops, 2021, pp. 1905-1914
- 公式コード(RealESRGAN):https://github.com/xinntao/Real-ESRGAN
- 公式コード(前提ライブラリ):https://github.com/xinntao/BasicSR
- 非公式コード(RealESRGAN):https://github.com/Lornatang/ESRGAN-PyTorch
※公式コードはBasicSRというライブラリを前提としていて、特にモデル構造はライブラリをまたいでネストおり、設計的にはあまりよくありません。サードパーティも参考にしつつ実装するのがおすすめです。
まずはサンプルから
Real-ESRGANでどの程度綺麗になるか見てみましょう。公式リポジトリからの引用です。アニメ動画用のモデルが提供されていました。Qiitaがvideoタグでの動画再生に対応してなかったため、スクショでの貼付けをします。実際は動画のデモがありますので、公式リポジトリを参照してください1。
Real-ESRGANは超解像モデルなので、出力解像度は入力解像度より大きくなりますが、比較のために並べています。
また、Real-ESRGAN、1枚の画像から1枚の画像への超解像(Single Image Super Resolution)なので、例えばTecoGANに代表されるような動画の超解像技術とは異なります。動画の超解像はフレーム間の情報を考慮しています。画像の超解像はいくらフレームがあっても、あくまでフレーム単位で拡大します。
フォントの部分はうまくいく場合と、やりすぎな場合もあります。ただ、特にReal-ESRGANはなめらかにする効果があるので、アニメ塗りは強そうです。
Real-ESRGANのポイント:低解像度データの作成プロセスの改良
Real-ESRGANのポイントとして抑えておきたいのは、前処理の改良、特に訓練時の低解像度データの作成プロセスの改良です。これ以外はそれほど大きな変更はありません。
具体的には、高解像度の訓練画像($y$)から、低解像度の入力画像($x$)を作るためのプロセスをよりリアルな世界のデータに近づけるということです。
一般的な超解像モデルでは、低解像度の画像の生成はBicubic法など単なるリサイズで脳死で作ってしまうのですが、「実世界の画像ではもっと複雑な画像劣化があるよ」と述べているのがこのReal-ESRGANです。実世界の画像劣化の理由を上げると、
- カメラのブレ
- センサーノイズ
- シャープネス処理
- JPEG圧縮
- SNSに上げたときのリサイズやノイズ
- それらをダウンロードして再アップロードしたときの連鎖的な劣化
例えば、よくフリー素材をSNSで使いまわしてると「アップロードのたびに画像が劣化してノイズが酷くなった」と言われることがあります。この現象に着目し、前処理を改良したのがReal-ESRGANです。論文では「高次の劣化」と述べています2。高次の劣化とは再アップロードや再エンコードなどによる連鎖的な画像の劣化です。
もし前処理の改良をせずに、低解像度の画像をBicubic法で脳死してしまうと、訓練の低解像度のデータと実世界の低解像度のデータ間で分布ミスマッチがおき、テスト時に余計なアーティファクトが観測されてしまいます。
これは訓練時のデータではなく、実世界のデータで見ています。左がただBicubic法で拡大した場合、2番目が前処理の改良をしないリファイン前のESRGAN、3番目がRealSRという別の先行研究、右が本論文(Real-ESRGAN)です。下段の画像がわかりやすいのですが、特にESRGANでは背景に余計なノイズが載っていますね。上段と中段も、ESRGANとBicubicがあまり差がないように見えます。前処理を改良すれば一番右のように綺麗に出るのが面白いです。個人的には論文開いたときに、1ページにビスマルクの画像が出てきたのでびっくりしました。
このようなノイズ、特に論文では「リンギングやオーバーシュート」に焦点を当てています。リンギングは特に輪郭線の周りで出やすいです。上段の髪、中段の枝や、下段の輪郭線がこれらの現象が出やすい場所でしょう。
画像劣化のシミュレーションプロセス
実際に前処理の改良といっても、「どのように現実世界の画像劣化をエミュレートしつつ、訓練時の低解像度画像を作るのか?」という点ですが、これが本論文のパイプラインであり、またキー手法にあたるものです。
「First order」「Second order」という2つの次元(Order)に分かれているのがわかります。ここでの次元(Order)は数学的な意味と異なり、単なるステージと思ったほうがいいです。「Blur→Resize→Noise→JPEG」という一連のプロセスを2ステージに渡って適用するという意味です。
超解像で「Second order」というと、数学的な(微分の)意味で2次のAttentionを使った「SAN」という論文があるのですが、これのSecond orderとは意味が全く異なります。最初その意味で使っているのかなと読んでいたら、単なる2ステージだったので安心2しました。あくまで「高次の劣化」のエミュレートのために2次と言っているだけです。
個々のコンポーネントについて見ていきましょう。
ぼかし(Blur)
Real-ESRGANのぼかしはかなり凝っています。
一般のガウシアンぼかし
ぼかしは畳み込み処理の1つなので、正規分布を用いた畳み込みカーネルで表現されます。カーネルは$(2t+1)\times (2t+1)$の行列です(カーネルサイズは奇数のほうが都合がいいので、こう表記しています)。今カーネル$\boldsymbol{k}$の$(i, j)\in[-t, t]$番目の要素を$\boldsymbol{k}(i, j)$とすると、
\boldsymbol{k}(i,j)=\frac{1}{N}\exp(-\frac{1}{2}\boldsymbol{C}^T\boldsymbol{\Sigma}^{-1}\boldsymbol{C}), \quad \boldsymbol{C}=[i, j]^T\tag{1}
\begin{align}\boldsymbol{\Sigma}&=\boldsymbol{R}\begin{bmatrix}\sigma_1^2 & 0 \\ 0 & \sigma_2^2 \end{bmatrix} \boldsymbol{R}^T\\ &= \begin{bmatrix}\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix}\sigma_1^2 & 0 \\ 0 & \sigma_2^2 \end{bmatrix} \begin{bmatrix}\cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix} \end{align}
$N$は正規化定数、$\boldsymbol{R}$は回転行列、$\boldsymbol{\Sigma}$は分散共分散行列を示します。$N$はカーネルの合計が1になるように正規化します。自分は「ぼかしって回転関係あるの?」と驚いてしまいましたが、後でサンプル見るとわかります。回転はとりあえずおいておきます。
$\sigma_1^2, \sigma_2^2$は分散のパラメーターですが、
- $\sigma_1^2=\sigma_2^2$:対称ガウシアンぼかしカーネル(isotropic
Gaussian blur kernel) - $\sigma_1^2\neq \sigma_2^2$:非対称カーネル(anisotropic kernel)
ガウシアンカーネルの典型例
よくガウシアンぼかしのカーネルとして、3×3の場合、
\boldsymbol{k}=\frac{1}{16}\begin{bmatrix}1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{bmatrix}
というカーネルが紹介されます。これは$\sigma_1^2=\sigma_2^2$の対称カーネルかつ、回転角$\theta=0$の(回転行列が単位行列になる)場合です。これをもっと一般に拡張したのが先程の式です。Real-ESRGANではさらにこれを拡張します。
対称・非対称のガウスぼかしの可視化
「非対称のガウスぼかしとは何か」「回転を伴ったガウスぼかしとはなにか」という点は気になります。普段あまり使わないぼかしです。
対称カーネルの場合はカーネルサイズを大きくすればするほど一律にぼやけています。回転が意味を伴ってくるのは非対称カーネルです。非対称カーネルを可視化すると、回転した楕円のような形になります。これによって矢印で示したような、斜め方向のぼかしをコントロールできます。多分リンギングに効くのではないかと思います。
一般ガウス分布によるぼかしカーネル
Real-ESRGANでは式(1)の他に、指数関数内にべき乗を含んだ「一般ガウス分布(generalized Gaussian)」を考えます。
$$\frac{1}{N}\exp\Bigl(-\frac{1}{2}(\boldsymbol{C}^T\boldsymbol{\Sigma}^{-1}\boldsymbol{C})^\beta\Bigr) \tag{2}$$
この$\beta$は確率密度関数の尖り具合をコントロールします。この発想は次のPlateau-shapedでも同じです。
Plateau-shaped distribution
式(2)のガウスカーネルのほかに、「Plateau-shaped distribution」という別の確率分布をベースにしたぼかしも導入します。どのカーネルを使うかは、Data Augmentationのように確率的に選択をします。
Plateau-shaped distributionの確率密度関数は以下の通りです。
$$\frac{1}{N}\frac{1}{1+(\boldsymbol{C}^T\boldsymbol{\Sigma}^{-1}\boldsymbol{C})^\beta} \tag{3}$$
Plateauとは「台地」を意味する単語ですが、$\beta$の値を変えて確率密度関数をプロットすると、以下のようにだんだんエアーズロックの断面のようになってきます。これはより$\beta$を大きくしたほうが、一般ガウスよりもPlateau-shapedのほうが台地っぽくなることがわかります。
カーネルの色のプロット(右)がわかりやすく、$\beta$が同一でもPlateau-shapedのほうが裾野の広がりが少ない「ギュッとしまった」カーネルになります。とにかくいろんなぼかしのカーネルを使いたいと認識しておいてください。
Sinc関数のカーネル
sinc関数によるカーネルも導入します。このカーネルはぼかしモジュールにおいて「普通のガウス・一般ガウス・Plateau-shaped」or「sinc関数」のように運用しますが、2nd orderのJPEGの最後にも適用するので、ぼかしとは若干扱いが異なります。sincカーネルは次の通りです。
$$\boldsymbol{k}(i, j)=\frac{\omega_c}{2\pi\sqrt{i^2+j^2}}J_1(\omega_c\sqrt{i^2+j^2})$$
ここで$J_1(\cdot)$は第1種ベッセル関数の第1オーダー(実装上はscipy.special.j1を使います)、$\omega_c$はカットオフ周波数、$(i, j)$はカーネルの座標を示します。
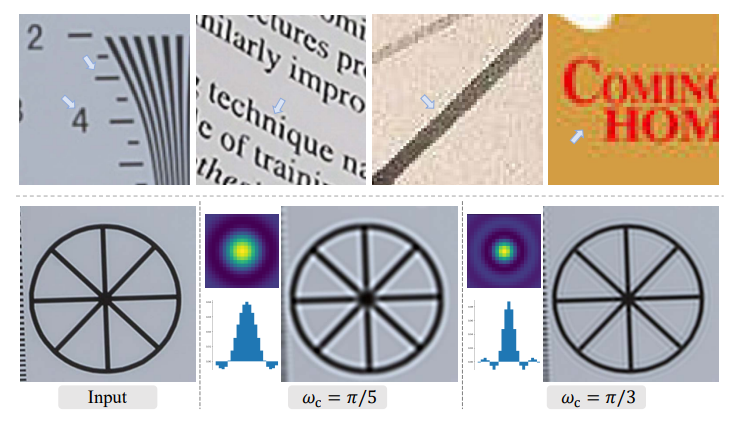
sinc関数が関連するのはリンギングやオーバーシュートで、上の図はリアルなデータのリンギングやオーバーシュート。下の図はカットオフ周波数$\omega_c$を変えた時の、カーネル値と畳み込み適用後の結果です。sinc関数によってリアルな画像の劣化である、リンギングやオーバーシュートをある程度再現できています。
ぼかしのパラメーター
いろんな分布のもとでのぼかしのカーネルを見てきましたが、ぼかしのモジュールの(ハイパー)パラメータを列挙すると次の通りです。
-
sinc関数を使うか、ぼかしを使うか:確率。ぼかしでいくのかsincでいくのかが最初の分岐。
- カーネル関数の選択:ぼかしの場合のみ。ごく普通のガウス分布(式1)、一般ガウス分布(式2)、Plateau-shaped(式3)の確率。
- カーネルの標準偏差:ぼかしの場合のみ。$\sigma_1, \sigma_2$
- カーネルの回転角:ぼかしの場合のみ。$\theta$
- カーネル関数の$\beta$:ぼかしのみ。なおかつ一般ガウス分布、Plateau-shapedの場合。
- sincのカットオフ周波数:sincの場合のみ。$^omega_c$
- カーネルサイズ:カーネル行列のサイズ。奇数
これらのパラメーターはData Augmentationのようにサンプル単位で確率的に決めます。具体的には。
-
sinc関数を使うか、ぼかしを使うか:10%でsinc、それ以外はぼかし。
- カーネル関数の選択:ぼかしの場合のみ。ガウス=70%、一般ガウス=15%、Plateau-shaped=15%
- カーネルの標準偏差:ぼかしの場合のみ。1st orderでは$[0.2, 3]$、2nd orderではは$[0.2, 1.5]$
- カーネルの回転角:ぼかしの場合のみ。$\theta\in[-\pi, \pi]$
- カーネル関数の$\beta$:ぼかしのみ。一般ガウス分布の場合$[0.5, 4]$、Plateau-shapedの場合$[1, 2]$
- sincのカットオフ周波数:sincの場合のみ。$^\omega_c$はカーネルサイズ13より小さい場合は、$[\pi/3, \pi]$、13以上の場合は$[\pi/5, \pi]$
- カーネルサイズ:カーネル行列のサイズ。7以上21以下の奇数
この他に、2nd stageのぼかしのモジュール全体を20%の確率でスキップします。
一部論文に記載されていないパラメーターもありますが、詳細はこちらのコードに載っています。
リサイズ
これは単にリサイズのモードを選ぶだけです。実装ではF.interpolateのmodeを「area, bilinear, bicubic」の3種類を等確率で選択していました3。リサイズによってはオーバーシュートのある画像や、ぼやけた画像を生成するので積極的にいろんな方法を使います。ただ、Nearest Neighborはミスアライメントの問題があるので除外しています。
この図は最初に4倍のダウンサンプリングを行い、元の解像度にアップサンプリングした例です。確かにNearestは位置ずれをおこしそうです。「area」はもしかしたら、あるパッチ内の平均を取るのかもしれませんね。Bicubic→BicubicはPSNRのような数値評価ではおそらく一番良いのでしょうが、オーバーシュートが出やすいように見えます。
また、リサイズは縮小だけでなく拡大も行います。画像劣化を積極的に起こすためだと思われます。具体的には「拡大」「縮小」「解像度維持」をランダムにとります。これでは解像度が保証されないので、2nd stageが終わったあとに望んだ低解像度になるように調整を行います。
リサイズのハイパラ
論文には言及がなかったのでコードを見ました。実験により変わるのかもしれませんが、
- 拡大:縮小:維持の確率:1st stageは「20%, 70%, 10%」、2nd stageは「30%, 40%, 30%」
- リサイズのレンジ:1st stageは$[0.15, 1.5]$、2nd stageは$[0.3, 1.2]$
- リサイズのモード:「area, bilinear, bicubic」を等確率
ノイズ
ノイズはガウス分布によるノイズ、ポアソン分布によるノイズの2つを使い分けます。どちらもそれぞれの分布からサンプリングして足すだけです。
また、足し方も使い分けており、RGBの各チャンネルに別々のノイズを足すカラーノイズ、全てのチャンネルに共通の値を足すグレーノイズの2種類があります。
実際にノイズを使い分けた結果がこの図で、ガウスとポアソンの違いは、ポアソンのほうが画素値に連動してノイズがかかります。建物の屋根の部分は画素値が小さいですが、ポアソンはほとんどノイズの影響がないのに対し、ガウスは画素値に関係なくノイズが乗っています。
ノイズをかけたあとに画像全体を「0-1」のレンジにクリップしています。
ノイズのハイパラ
- ガウスかポアソンかの確率:50%ずつ
- ガウスノイズのパラメーター:1st stageはガウスノイズの標準偏差は$[1, 30]$、2nd stageは各$[1, 25]$。ちなみに平均は0。
- ポアソンのパラメーター:1st stageはポアソンのスケールは$[0.05, 3]$。2nd stageは$[0.05, 2.5]$。
- グレーノイズの確率:40%。グレーノイズの場合はチャンネル間で共通、それ以外はチャンネル間で独立のノイズをかける
JPEG
JPEG圧縮を「DiffJPEG」という微分可能なJPEGライブラリで行います(多分微分可能よりもGPUで高速化したかったから)。JPEGのパラメーターは品質のみで、$[30, 95]$で設定しています。
2nd stageのJPEG以降
2nd stageのJPEG以降はまた追加で処理が入ります。以下の2パターンです。
- パターン1
- 入力画像で求められる解像度へ変更(リサイズ方法はリサイズモジュールと同様3択)
- 80%の確率でぼかしモジュールのsincを適用
- JPEGモジュールのJPEG圧縮を適用
- パターン2
- JPEG圧縮
- 求められる解像度へ変更
- 80%の確率でsinc
パターン1と2は順番が違うだけです。パターン1と2は50%の確率で分岐します。
以上で、Real-ESRGANの訓練時の低解像度データの作成が終わりました。非常に複雑なパイプラインでした。
モデル構成
Generatorはほぼ同じ
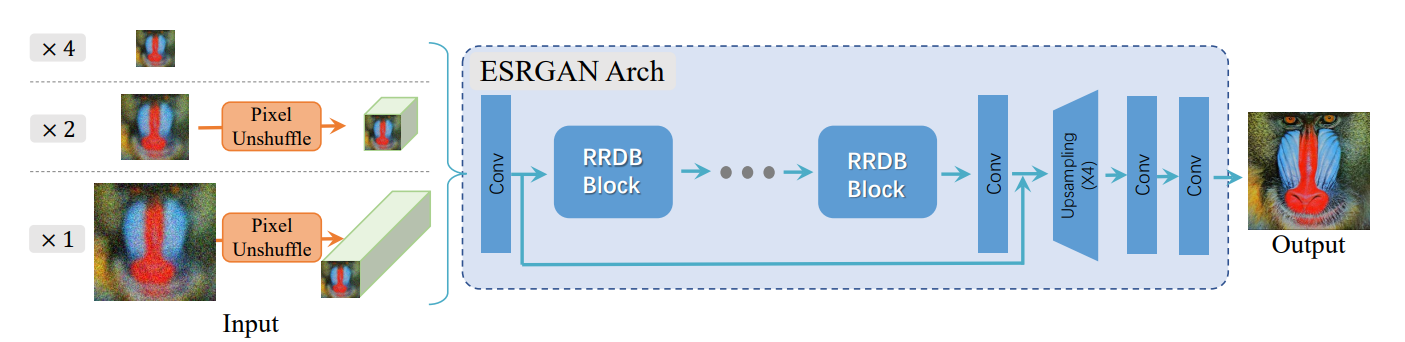
モデル構成はESRGANとそれほど大きくは変わっていません。図を掲載しましょう。
GはESRGANと同じですが、Pixel Unshuffle(Pixel Shuffleの逆操作)を適用するように変わっています。空間方向のデータをチャンネル方向に変換し、空間方向の計算量を減らすテクニックです。
RRDBとはESRGANのモジュールで、「Residual in Residual Dense Block」を意味します。Residual BlockながらDenseNetのような構造を持つモジュールです(これはESRGANからの論文の引用です)。
公式実装のモデル構造のソース探すのなかなか大変だったのですが、気になる方はこちらを参照してください。
- 公式:https://github.com/xinntao/BasicSR/blob/afae255d1b49e0dcfd388007a84a1ef7d672e30d/basicsr/archs/rrdbnet_arch.py
- サードパーティ:https://github.com/Lornatang/ESRGAN-PyTorch/blob/master/model.py
DiscriminatorはSNのついたU-Netに
DiscriminatorはU-Net-likeなモデルにし、訓練の安定化のためにSpectral Normalizationを導入しています。大量の画像の劣化を導入したことで、従来のESRGANよりも高い識別能力が必要になり、U-Netのような大きなモデルが必要になったためです。Spectral NormalizationはGANの安定化のほか、オーバーシャープやその他の望ましくないアーティファクトを緩和することにも寄与しているとのことです。
訓練詳細
- データはDIV2K、Flickr2K、OutdoorSceneTraining(ESRGAN)と同じ
- 高解像度の画像のパッチサイズ(出力解像度)は256
- 訓練GPUはV100を4枚(ちょっと多い)
- バッチサイズは48
- オプティマイザーはAdam
- 学習率2e-4でGをL1ロスのみで1M iter訓練。次に学習率1e-4でGとDを足して「L1ロス+Perceptual Loss+GANのAdversarial Loss」で400k iter訓練。
- GANのモデルとして訓練する時の係数は、L1=1、Perceptual=1、GAN=0.1
- Perceptual Lossの計算は訓練済みVGG19を使い、
conv1, ……, conv5の特徴マップで比較。係数はconv1, conv2は0.1、それ以外は1 - D:Gのアップデート回数比は特に記述がなかったので、おそらく1:1。
訓練時の高解像度の画像にアンシャープマスクをかける(Real-ESRGAN+)
出力画像について、目に見えるアーティファクトを抑えてより鮮明にさせるトリックがあります。高解像度の教師データ$y$側に、アンシャープマスクをかけて訓練します。
推論後の画像にアンシャープマスクをかけるのが一般的ですが、これはオーバーシュートが発生する傾向があります。訓練データに対してアンシャープマスクをかけたほうが、オーバーシュートの抑制と鮮明化のバランスを取りやすくなる傾向にあります。
訓練時に$y$にアンシャープマスクをかけたものが「Real-ESRGAN+」、かけないものが「Real-ESRGAN」です。比較すると、
特にこのモデル、アニメ塗りに対してすごく強いですね。アニメ塗りはReal-ESRGAN+が一番いいです。低解像度のデータの生成で、ぼかしを多様しているため、出力画像がのっぺりとする傾向があります。
3つ目のれんがのテクスチャは、元のコンテクストがどの程度かわかりませんが、若干レンガ特有の質感を失っているように見えます。ただそれでも他のモデルよりかはいいです。自然の画像にアンシャープマスクをかけるかどうかは好みありそうです。Image to image translationでは「元のコンテクストをどれぐらい残すのか」が普遍的に問題になるので、どの程度出力画像に対しての「味付け」を許容するかは難しそうです。
1枚目の文字はなんともいえないですね。他の手法はぼけているのは確かですか、Real-ESRGAN+がいいかと言われると「K」の部分にアーティファクトができているので、アンシャープマスクをかけないReal-ESRGANのほうがいいかもしれません。ただ、Conv2Dのみのフォントの拡大は文字のスケルトンが歪む傾向があるので、もしかすると他の文字特化のモデルで使われているような工夫を入れたほうがいいかもしれません。このアドベントカレンダーでも、13日目に紹介した「DG-Font」がフォントの生成に特化したモデルでしたが、Deformable Convを入れています。あるいは、14日目に紹介したLaMaは文字特化ではありませんが、Perceptual Lossの計算にセグメンテーション問題で訓練したモデルを使っているため、ここらへんの改良の余地はありそうです。ただ、個人的にはアニメはReal-ESRGAN+でいいと思います(テロップのようにフォントが入ると難しそうです)。
定性・定量評価
この論文、正直定量評価が難しいです。これまでの研究と低解像度の生成方法を変えているので、そもそも「同一の問題とみなしていいのか」という疑問があります。また、実世界の画像に焦点を当てたものなので、DIV2K、Flickr2Kのような「訓練で使ったデータセットで評価するのが正しいかどうか」もわかりません。なので、定量評価はあくまで参考で、主観的な評価が中心になってしまうのが仕方のないところでしょう(Ablation Studiesも主観評価です)。
NIQEという知覚ベースのスコアを定量評価としています。低いほうがいいです。データセットは訓練以外のものを使い、例えばImageNetのようなデータセットを「実世界の画像」として参照しています。おおよそReal-ESRGANのほうがいいですが、「ImageNetについては改良前のESRGANのほうが明らかに良いという謎の結果」を出しているので、この定量評価がどの程度信頼できるものかは疑問が残りそうです。
高次の劣化とsincフィルターの効果
2nd orderの劣化と、sincフィルターをそれぞれ除外した場合です。2nd orderの劣化がないと境界線周辺のノイズ(屋根やトラクターの周り)が目立つようになります。
sincフィルターは結構効いていて、ない場合の字や線の周りにリンギングをある程度抑制できています。テキストだとsincフィルターは重要になりそうです。
Discriminatorのアーキテクチャ
Real-ESRGANではDの構造を変更していましたが、この影響を調べます。ESRGANはU-Netではありません。「U-Net Discriminator」は提案手法からSpectral Normalization(SN)を引いたもの、「U-Net Discriminator w/SN」が提案手法です。
ESRGANの設定ではそもそも枝がぼやけてしまっています。U-Netのようなある程度大きいDiscriminatorモデルが必要と述べているのはこういうことです。SNのありなしで見ると、SNがない場合だと枝の周りにアーティファクトが観測されています。SNがGANの安定化だけでなく、性能の向上にも寄与しているというストレートな結果です。
このGANの訓練プロセスを見ると、L1で先に相当訓練しているので計算リソースとしては軽そうです。「SNをつけると訓練が遅くなったり、D:Gのアップデート回数を2:1や5:1のようになるからいらない」という研究もあるのですが、1:1で十分な効果が出ているのは面白いです。L1で相当訓練していますし、Adversarial Lossの寄与度もかなり低く、安定性としては高めのGANだと思います。
U-Netがなぜうまく行くかというのは自分の解釈ですが、Skip Connectionで低レベルの特徴を使いまわしたほうが超解像度のGANとしてはいい(つまりセマンティックセグメンテーションのアプローチと似ている)のが背景にあるのではないかと思います。おそらくですが、Perceptual Lossで分類ベースで訓練した係数よりも、LaMaでやっているようにセマンティックセグメンテーションで訓練した係数のほうが、アーティファクトの軽減や境界を鮮明にするという点ではうまくいくのではないかと自分は思います。ただ、テクスチャへの影響がどの程度のものかはやってみないとわかりません。
ぼかしカーネルの種類
この手法では「ぼかしのカーネルのバリエーションをもたせる」ということが重要になっていました。「普通のガウス分布によるぼかしカーネル」だけの場合と、本研究のように「普通のガウス+一般ガウス分布+Plateau-shaped」を組み合わせたケース(More blur kernekls)で比較します。
組み合わせたほうが境界が鮮明になります。ガウスぼかしだけの場合は境界が曖昧になりがちです。一般ガウス分布やPlateau-shapedは先程見たように、円盤状のカーネルをしているため、境界の鮮明さに対してはうまくアプローチできるのでしょう。
このモデルの限界
ビルの線やメッシュのような繰り返しのパターンで、歪みが生じるとのことです。
そういえばこの問題にフォーカスした論文ありましたよね。そうです。InpaintingのLaMaがまさにこの問題に対処していました。LaMaではフーリエ変換してConvするか、Dilated Convをするとこのような現象を改善できるとあったので、最低でもGにDilated Convを入れるとマシになるのかもしれません。フーリエは少し重いので効果次第でしょう。Inpaintingと超解像度は問題としては近い関係にあります。
まとめと感想
この論文では超解像度モデルを実世界のデータにあわせるために、適切な前処理の提案(訓練時の低解像度画像の生成方法の改良)が大きな貢献でした。研究というよりかは、「訓練時の理想設計と実世界のギャップを埋める」というエンジニアリング寄りな内容で、前処理1個とってもこれだけ考える要素あるのかと驚かされました。実際はData Augmentationに近いので、「分布差を埋めるためのData Augmentation」の典型例でしょうね。発想としては「実世界の画像劣化とはこういうものだから、こういう前処理/Augmentationを提案します」という筋の通ったスタイルです。超解像度として必要でなくても、このようなAugmentationは機械学習の問題一般としてよく遭遇するので、考え方が参考になりそうです。
Real-ESRGAN単体として見ると、デモでもアニメ画像に対して適用した例を多く表示していました。論文を読んでわかる通り、アニメ塗りに対してとにかく強いので、アニメへの応用というアプローチで実装するのも楽しそうです。
これで1人アドベントカレンダーは25日中、24日分が終わりました。いよいよ次は最後の記事YOLO Xです。
告知
このアドベントカレンダーが本になりました!
https://koshian2.booth.pm/items/3595424
Amazonでも扱いあります詳しくは👉 https://shikoan.com