2021年のディープラーニング論文を1人で読むAdvent Calendar14日目の記事です。GAN5連続の記事の最後の記事です。今回紹介するのはInpainting(画像修復)の論文で、高速フーリエ変換と畳み込みを組み合わせた今までとは全く異なる研究です。
InpaintingやGANでは広域の特徴量が重要であると言われてきました。FFTを使ったシンプルな畳み込みモジュールを使い、周波数ドメインの特徴マップをグローバルな特徴量としています。256pxで訓練してフルHDに近い解像度で推論しても性能が落ちにくいどころか、ドメイン間の転移もある程度のロバスト性があるというかなりびっくりな論文です。個人的にはかなり刺さる内容でした。
著者はモスクワとソウルのサムスンAIのチームが中心です。WACV 2022に採択されています。
- タイトル:Resolution-robust Large Mask Inpainting with Fourier Convolutions
- URL:https://arxiv.org/abs/2109.07161
- 出典:Suvorov, Roman and Logacheva, Elizaveta and Mashikhin, Anton and Remizova, Anastasia and Ashukha, Arsenii and Silvestrov, Aleksei and Kong, Naejin and Goka, Harshith and Park, Kiwoong and Lempitsky, Victor; arXiv preprint arXiv:2109.07161
- コード:https://github.com/saic-mdal/lama
- プロジェクトページ:https://saic-mdal.github.io/lama-project/
高速フーリエ変換(FFT)を使った畳み込みとは何?
OpenCVでの畳み込み
画像処理の畳み込みはニューラルネットワークの関数として表現できます。例えば、ガウシアンぼかしは画像処理の畳み込みの基本的な例です。畳み込みカーネルを、
\frac{1}{16}\begin{bmatrix}1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1\end{bmatrix}
とすると3×3のガウシアンぼかしとなります。OpenCVでは、次のように書けます。
import cv2
import numpy as np
import matplotlib.pyplot as plt
def opencv_conv():
img = cv2.imread("lenna.png")
img = cv2.resize(img, (128, 128)) # 結果がわかりやすいようにリサイズする
kernel = np.array([[1, 2, 1], [2, 4, 2], [1, 2, 1]], np.float32) / 16.0
result = cv2.filter2D(img, -1, kernel)
plt.imshow(result[..., ::-1]) # BGR->RGB
plt.show()
このようにぼやけた画像が表示されました。
画像処理の畳み込みのニューラルネット表現
OpenCVでの畳み込みをニューラルネットワークの関数(Conv2D)として表現しましょう。PyTorchでは次のように書けます。
import torch
import torchvision
import torch.nn.functional as F
import matplotlib.pyplot as plt
def pytorch_conv():
img = torchvision.io.read_image("lenna.png").unsqueeze(0) / 255.0 # (1, 3, 512, 512)
img = F.interpolate(img, size=(128, 128), mode="bilinear", align_corners=False) # 結果が見やすいようにリサイズ
# 画像処理のガウシアンぼかしのカーネル
gaussian_kernel = torch.FloatTensor([[1, 2, 1], [2, 4, 2], [1, 2, 1]]) / 16.0
# Conv2D用に拡張(チャンネル単位に作用するようにする)
conv_kernel = torch.eye(3)[..., None, None] * gaussian_kernel[None, None, ...] # (3, 3, 3, 3)
result = F.conv2d(img, conv_kernel, padding=1)
plt.imshow(result[0].permute(1, 2, 0)) # CHW -> HWC
plt.show()
チャンネル単位にガウシアンぼかしのカーネルを作用させると、画像処理の畳み込み(ガウシアンぼかし)のニューラルネットワーク表現になります。実際のConv2Dはチャンネル間の演算も可能なので、もっと処理が広いです。ここは今回の論文とは直接関係ないので「そうなんだ」程度に流してください。
この通り、OpenCVと同様にぼかしができています。
FFTでの畳み込み
今回のテーマのFFTの畳み込みです。この論文では、画像のFFTを次のように実装しています。
torch.fft.rfftn(orig, dim=(-2, -1), norm="ortho") # [N, C, H, W/2+1]
この出力は$(N, C, H, W/2+1)$の複素数になります。もともと画素値が実数なので、それを複素数にマッピングした分、横方向の解像度が半分になったという形ですね。今回はFFTの紹介ではないので、この結果の詳細な解釈は割愛しますが、空間的なドメインから周波数のドメインにマッピングされた特徴量です。音声のスペクトログラムの2次元版と考えてください。
FFTでの畳み込みは、FFTした結果の実部と虚部にそれぞれConv2Dをかけることです。Conv2D自体は通常の実数の畳み込みと変わらなくて、複素数の実部と虚部をそれぞれ実数とみなし、畳み込みをするだけです。
レナの画像を「FFT→実数部分or虚数部分にガウシアンぼかし→逆FFT(IFFT)」としたときの結果は以下の通りになります。(1)恒等変換<FFT→IFFTしただけでぼかしはなにもかけていない>、(2)実数部分のみぼかし、(3)虚数部分のみぼかし、(4)実数部分と虚数部分の両方にぼかし の4パターンで比較してみましょう。
import torch
import torchvision
import torch.nn.functional as F
import matplotlib.pyplot as plt
def subplot(x, nr, nc, i, title):
minval = x.min()
maxval = x.max()
img = (x-minval)/(maxval-minval)
plt.subplot(nr, nc, i)
plt.imshow(img)
plt.axis("off")
plt.title(title)
def main():
orig = torchvision.io.read_image("lenna.png").unsqueeze(0) / 255.0 # (1, 3, 512, 512)
# 画像処理のガウシアンぼかしのカーネル
gaussian_kernel = torch.FloatTensor([[1, 2, 1], [2, 4, 2], [1, 2, 1]]) / 16.0
# Conv2D用に拡張
conv_kernel = torch.eye(3)[..., None, None] * gaussian_kernel[None, None, ...] # (3, 3, 3, 3)
# fft
fft = torch.fft.rfftn(orig, dim=(-2, -1), norm="ortho") # (1, 3, 512, 257): 複素数
blur_real = F.conv2d(fft.real, conv_kernel, padding=1)
blur_imag = F.conv2d(fft.imag, conv_kernel, padding=1)
# 実部or虚部で場合分け
identity = torch.fft.irfftn(torch.complex(fft.real, fft.imag), dim=(-2, -1), norm="ortho")
real_only = torch.fft.irfftn(torch.complex(blur_real, fft.imag), dim=(-2, -1), norm="ortho")
imag_only = torch.fft.irfftn(torch.complex(fft.real, blur_imag), dim=(-2, -1), norm="ortho")
both = torch.fft.irfftn(torch.complex(blur_real, blur_imag), dim=(-2, -1), norm="ortho")
for i, (im, title) in enumerate(zip([identity, real_only, imag_only, both],
["Identity", "Real Only", "Imag Only", "Both"])):
subplot(im[0].permute(1, 2, 0), 2, 2, i+1, title)
plt.show()
if __name__ == "__main__":
main()
FFTしないガウシアンぼかしだと近傍ピクセルのみ影響しましたが、FFTしてから周波数のドメインでガウシアンぼかしをかけるともっと大域に影響しているのがわかります。(逆FFT後の値は0-1に収まる保証がないので、可視化用にMin-Maxスケーリングして0-1におさめています)。
あくまでガウシアンぼかしだけで見ると、虚数部分への畳み込みが面白そうです。髪の形状を伴ったまま他の場所に転移できていますし、目や口などのパーツ単位でのコピペに成功しています。実数と虚数両方畳み込むのも興味深く、例えば四角形や境界線のような線の表現で有用ではないかと思われます。
これを画像修復(Inpainting)で応用しようとしたのが、本論文の特徴です。
FFTによる畳み込みモジュールの元ネタ
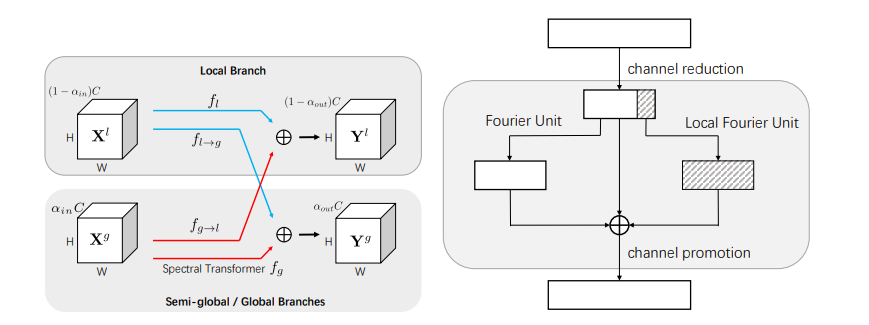
本論文で使っているFFTを使った畳み込みモジュールには元ネタがあります。NeurIPS 2020に採択されたFast Fourier Convolutionという論文です1。元ネタの論文からの引用です。
Fast Fourier Convolutionでは、フーリエ変換した結果をグローバルな特徴量として捉えています。フーリエ変換するとなぜグローバルな特徴量になるかというと、空間方向から周波数方向に変換しているためで、フーリエ変換後の1ドットというのは、元画像の1ピクセルに対応しません。事実先程のFFTした結果にガウスぼかしをかけた結果が、相当広範囲に影響を及ぼしています。「フーリエ変換をするとグローバルな特徴量とみなせるよ」というのが、本論文でも元ネタの論文でも大前提にあります2。
Large Mask Inpainting (LaMa)
Fast Fourier Convolution (FFC)
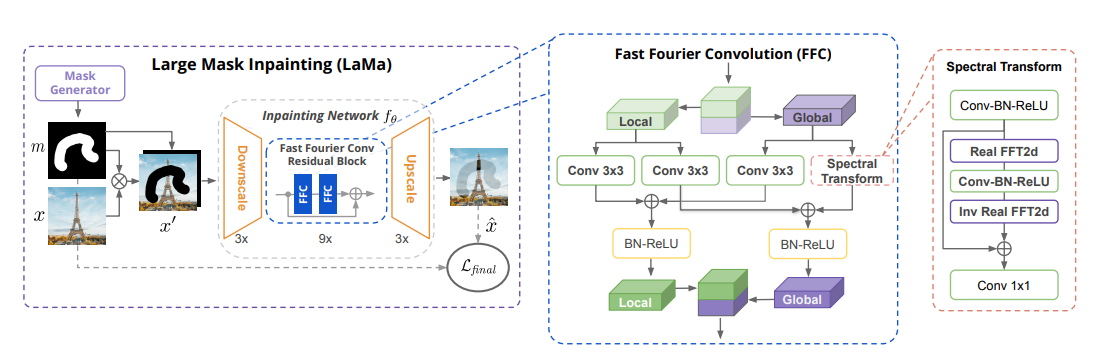
前置きが長くなってしまいましたが、本論文の手法解説にいきます。タイトルにもある**Large Mask Inpainting (LaMa)**が本論文の提唱手法です。LaMaでは、Fast Fourier Convolution (FFC)を使っています。モデル構成は次のとおりです。
LaMaの大きな特徴は、Residual BlockがFFCで構成されていることです。FFCは元ネタの論文とほとんど変わらず、Local-Globalでクロスしていくモジュール構成になっています。Localは普通のフーリエ変換をしない畳み込みです。FFTを使っている部分は「Spectral Transform」というモジュールです。このモジュールの計算フローについて、論文ではかなり詳細に書いていました。PyTorchの表記に合わせて書き直します。
まず入力画像が$\mathbb{R}^{C\times H\times W}$とします(次元はチャンネル数、縦解像度、横解像度)。画像なので実数($\mathbb{R}$)です。論文ではReal FFT2Dを適用すると書いてありますが、これはPyTorchのtorch.fft.rfftnを指します。最後の次元の負の周波数を省略することで、FFTを高速にしたものです。これにより、
- Real FFT2D: $\mathbb{R}^{C\times H\times W} \to \mathbb{C}^{C\times H\times (\frac{W}{2}+1)}$
ここで$\mathbb{C}$は複素数です。実数から複素数にマッピングした分、横方向の解像度が半分になっています。複素数のまま畳み込みをするのは困難なので、実部と虚部をそれぞれ実数としてチャンネル方向にくっつけます。これはチャンネル数が2倍になることを意味するので、
- ComplexToReal: $\mathbb{C}^{C\times H\times (\frac{W}{2}+1)} \to \mathbb{R}^{2C\times H\times (\frac{W}{2}+1)}$
となります。次に周波数ドメインでの畳み込みブロックを適用します。実装的には通常の畳み込みと変わりません。
- Relu→BN→Conv1×1: $\mathbb{R}^{2C\times H\times (\frac{W}{2}+1)} \to \mathbb{R}^{2C\times H\times (\frac{W}{2}+1)}$
逆FFTをしたいので複素数に戻します。先程と逆で、チャンネル方向で半分に切って、実部と虚部とします。
- RealToComplex: $\mathbb{R}^{2C\times H\times (\frac{W}{2}+1)} \to \mathbb{C}^{C\times H\times (\frac{W}{2}+1)}$
最後に逆FFT(Inverse Real FFT2D)を適用することで、最初のshapeに戻ります。
- Inverse Real FFT2D: $\mathbb{C}^{C\times H\times (\frac{W}{2}+1)} \to \mathbb{R}^{C\times H\times W}$
あとはよくある畳み込みネットワークのモジュールの実装です。
FFCの効果
FFCは特に窓やフェンスのような繰り返しの多いパターンで有効です。LaMaと同じ構成でFFCを外したケースが「LaMa-Regular」「LaMa-Regular(deep)」ですが、FFCを利用したLaMaよりも係数が多いにも関わらず、窓やフェンスの描画に失敗しています。
「フーリエ変換をすることで遅くなるのではないか」という疑問もあるかもしれませんが、LaMa-FourierはLaMa-Regularよりも平均して20%遅いだけだったとのことです。係数が倍近くあるLaMa-Regular(deep)よりかは早いのではないかと思われます。
High receptive field perceptual loss
本論文のコア要素として「High receptive field perceptual loss」という損失関数の工夫があります。Perceptual Lossとの大きな違いは、セマンティック・セグメンテーションで訓練したDilated ConvのあるResNet50の特徴量を使用していることです。
Perceptual Lossでよくあるケースは、分類問題で訓練したVGG16/19の特徴量求めて比較するというものでしたが、分類問題で訓練したモデルよりも、セマンティック・セグメンテーションで訓練したモデルの特徴量でロス計算したほうが良い結果が出たとのことです。
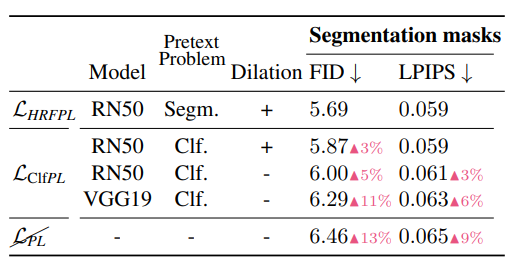
実際に比較してみると、分類問題で訓練したモデル(Clf)を使ったロスよりも、セマンティック・セグメンテーション(Segm)によるロスのほうがFIDやLPIPSでは良い結果が出ていることが確認できます。先行研究でも、分類問題のモデルはテクスチャにより注目する傾向にあることが報告されており、高レベルの情報が失われることが示唆されます。
**High receptive field perceptual loss(HRFPL)**の定義は以下のとおりです。
\mathcal{L}_{HRFPL}(x, \hat{x})=\mathcal{M}([\phi_{HRF}(x)-\phi_{HRF}(\hat{x})]^2)
ここで$x$は本物の画像、$\hat{x}$は生成された画像を示します。$\phi_{HRF}$は訓練済みモデル(セマンティックセグメンテーションで訓練されたDilated ConvのあるResNet50)の中間層の特徴量を示します。$\mathcal{M}$は層単位でロスを取り、さらに平均するというオペレーションです。
この式の処理が釈然としなかったのでコードで確認してみました。公式コードのResNetPLというのがHRFPLの実装です3
class ResNetPL(nn.Module):
def __init__(self, weight=1,
weights_path=None, arch_encoder='resnet50dilated', segmentation=True):
super().__init__()
self.impl = ModelBuilder.get_encoder(weights_path=weights_path,
arch_encoder=arch_encoder,
arch_decoder='ppm_deepsup',
fc_dim=2048,
segmentation=segmentation)
self.impl.eval()
for w in self.impl.parameters():
w.requires_grad_(False)
self.weight = weight
def forward(self, pred, target):
pred = (pred - IMAGENET_MEAN.to(pred)) / IMAGENET_STD.to(pred)
target = (target - IMAGENET_MEAN.to(target)) / IMAGENET_STD.to(target)
pred_feats = self.impl(pred, return_feature_maps=True)
target_feats = self.impl(target, return_feature_maps=True)
result = torch.stack([F.mse_loss(cur_pred, cur_target)
for cur_pred, cur_target
in zip(pred_feats, target_feats)]).sum() * self.weight
return result
forward内のself.implというのが、訓練済みニューラルネットワークです。何らかの特徴量をとっているわけですが、return_feature_maps=Trueのオプションがついているのが気になります。どの層の特徴量をとっているのでしょうか。
ResNet+Dilatedの場合のコードはこちらにあり、forwardの部分を抜き出すと
def forward(self, x, return_feature_maps=False):
conv_out = []
x = self.relu1(self.bn1(self.conv1(x)))
x = self.relu2(self.bn2(self.conv2(x)))
x = self.relu3(self.bn3(self.conv3(x)))
x = self.maxpool(x)
x = self.layer1(x)
conv_out.append(x)
x = self.layer2(x)
conv_out.append(x)
x = self.layer3(x)
conv_out.append(x)
x = self.layer4(x)
conv_out.append(x)
if return_feature_maps:
return conv_out
return [x]
とあるのがわかります。return_feature_maps=Trueだと、おそらく各Residual Blockの最後の値を出しているのではないかと考えられます。つまり、HRFPLもこれらの値に基づいて計算しているというのが確認できます。
またHRFPLの式の定義にあった$\mathcal{M}(\cdot)$というオペレーターですが、先程のResNetPLの実装を見る限りでは、層単位でMSEを取ったあとで、sumをとっている(後で平均につなげる?)ものでした。式や文章で見ると理解に苦しみましたが、コードで見ると単純な内容でした。
マスクを加味した敵対的なロス
この論文はGANを使っているので、敵対的なロスを使っているのですが、マスク(Inpaintingしようとする部分で入力に与えられる)を加味したロスになっています。Dでは画像全体の真偽を見分けるのではなく、pix2pixのようなパッチレベルでの真偽を見分けています。パッチレベルの真偽を$D_\xi(\cdot)$としたときに、敵対的なロス$\mathcal{L}_{adv}$は、
\begin{align*}\mathcal{L}_D=-\mathbb{E}_x\bigl[\log D_\xi(x)\bigr]-\mathbb{E}_{x, m}\bigl[\log D_\xi(\hat{x})\odot m\bigr]-\mathbb{E}_{x, m}\bigl[\log (1-D_\xi(\hat{x}))\odot (1-m)\bigr] &\\ \mathcal{L}_G=-\mathbb{E}_{x, m}\bigl[\log D_\xi(\hat{x})\bigr]\end{align*}
\mathcal{L}_{adv}=\rm{sg}_\theta(\mathcal{L}_D)+\rm{sg}_\xi(\mathcal{L}_G) \to \min_{\theta, \xi}
となります。一見通常のGANのロスと同じに思えるのですが、マスクによる掛け算が入っています。合成画像$\hat{x}$において、マスクされている部分(修復しようとする部分)のみを偽物とし、マスク以外の既知の部分は本物となるようにロスを組み立てています。$\rm{sg}(\cdot)$は勾配をストップさせるオペレーターで、通常のGANで行われている訓練するかどうかの切り替えに相当にします。
全体の損失関数
全体の損失関数は次の通りです。
\mathcal{L}_{final}=\kappa\mathcal{L}_{adv}+\alpha\mathcal{L}_{HRFPL}+\beta\mathcal{L}_{DiscPL}+\gamma R_1
$\mathcal{L}_{adv}, \mathcal{L}_{HRFPL}$はこれまで見てきたとおりです。$\mathcal{L}_{DiscPL}$は訓練の安定化のため、Discriminatorの中間層の値を、本物と偽物の間で近づけようとするいわゆるFeature Matching Lossです。Feature Matching Lossは他のGANでもよく使われるロスです。
$R_1$はGradient Penaltyの$R_1=E_x|\nabla D_\xi(x)|^2$です。
ハイパーパラメーターについては、$\kappa=10, \alpha=30, \beta=100, \gamma=0.001$を使用しています。敵対的なロスよりもFeature MatchingやHRFPLの割合が多く、個人的には比較的安定しそうなGANだなという印象を受けます。
マスクの戦略の見直し
マスク作成の戦略もこの論文の重要なポイントです。この論文では大きなマスクを訓練データに対して積極的に適用しています。
今までのマスク戦略はDeepFill v2やNarrow Masksのように、小さいマスクを大量に配置する戦略でした。この論文では、Large masks wideやLarge masks boxのような、大きいマスクを積極的に取り入れます。具体的には、Large masks wideやLarge masks boxのいずれかの戦略をランダムで選択します。
このような大きなマスクはInpaintingの一般論として難しいと思われていました。ところが、大きいマスクで訓練したほうが、大きいマスク相手の生成はもちろん、小さいマスク相手の生成に関しても部分的に有効であることを示しています。
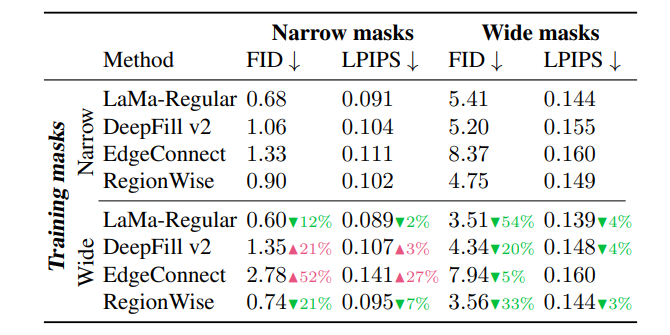
このマスク戦略は結果はLaMaだけでなく、DeepFill v2やEdgeConnect、RegionWiseといった他の先行研究に対しても検証しています。縦軸が訓練時のマスク戦略で、横軸が推論時のマスクの形状です。
大きいマスクで訓練し、大きいマスクで推論するときは全部のモデルで改善(FIDやLPIPSは低いほど良い)しているのはほぼ当たり前でしょう。しかし、大きいマスクで訓練し、小さいマスクで推論するときでさえも半数のモデルで改善しているのがわかります。特に提案手法のLaMaや先行研究のRegionWiseでは一貫して改善しています。
マスクの作成方法は論文の補助資料にコードつきで載っているので、気になる方は参照してみてください。
実験結果
有効な受容野の高速な成長が大事
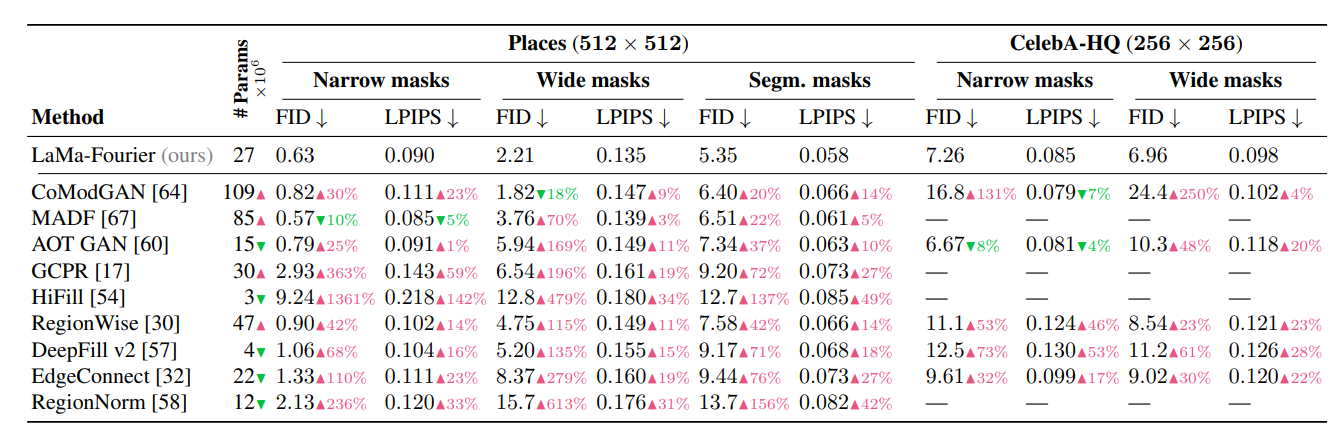
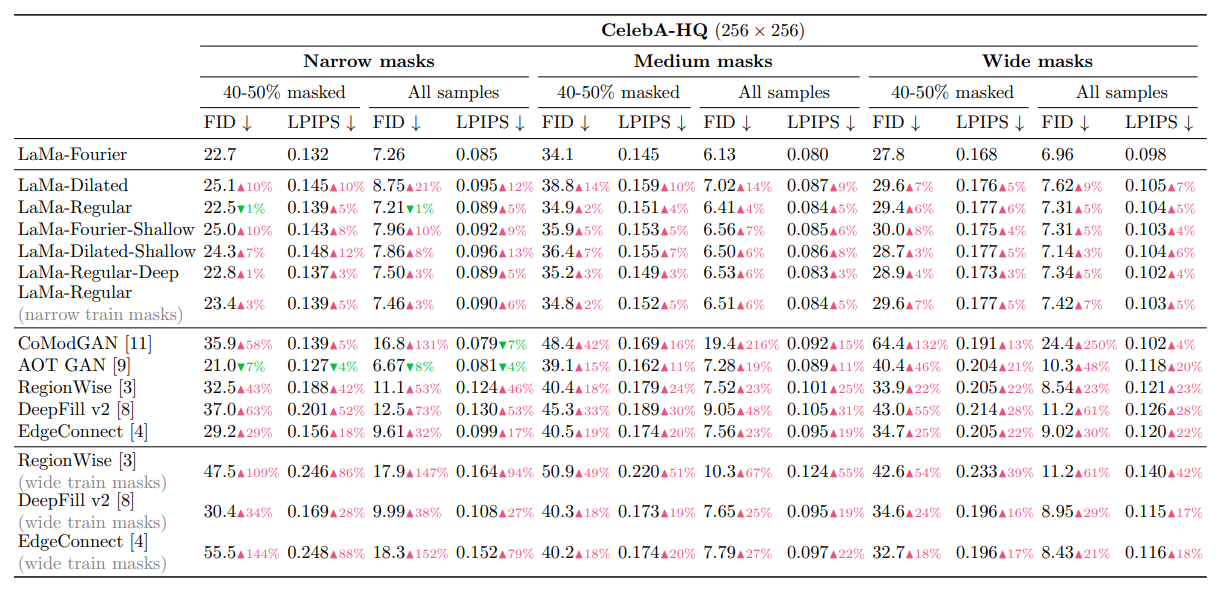
定量結果がこのとおりです。先行研究との比較は、「LaMa-Fourierに対して先行研究がどれだけ悪化しているか(赤)」を示しています。EdgeConnectに対してFIDで倍近い改善を取れているのがなかなかすごいです。特に大きいマスクでの改善が著しく、セグメンテーションマスクに対しては完勝です。大きいマスクに対してのこれだけの改善は、FFTでグローバルな特徴を取ったおかげであること。セグメンテーションマスクに対しては、HRFPLでセマンティックセグメンテーションのモデルをロス計算に使っていることが理由として考えられます。
この理由について論文ではもう少し突っ込んで考察しています。論文の冒頭で「従来の畳み込みネットワークでは、有効な受容野の成長が遅いという問題があり、初期層では受容野が不足する。そのためネットワークの多くの層では、大域的なコンテクストが不足し、コンテクストを作成するための計算やパラメーターが無駄になる」と仮説を立てています。FFTではなく、Dilated Convを使用してもInpaintingの性能が向上します。結局は「有効な受容野を早く成長させることが性能の向上につながる」と論文では結論づけています。
Dilated Convを代替として使った場合
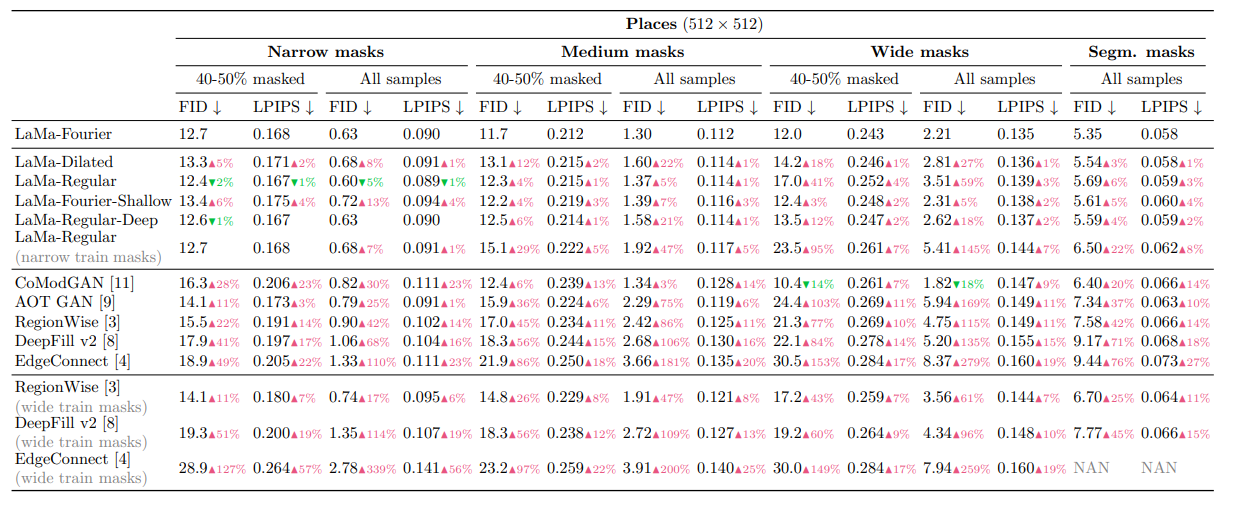
なお、FFTではなくDilated Convを使ったときにどの程度の性能なのかという点についてですが、これは論文の補助資料に載っています。
上からPlaces(512×512)、CelebA-HQ(256×256)で訓練したときの定量指標です。LaMa-Fourier基準で比較しています。Dilated Convを使ったケースが「LaMa-Dilated」で、Placesデータセットではかなり明確に差が出ており、特に大きいマスクでLaMa-Fourier>LaMa-Dilated>LaMa-Regularの傾向が明らかになっています。計算量はLaMa-FourierよりLaMa-Dilatedのほうが少ないので、ここは処理の重さとのトレードオフでしょうか。
ただ、LaMa-Fourier-ShallowはLaMa-Dilatedよりも大きく悪くなるマスクサイズがないので、計算量を軽くしたいのなら(1)フーリエを使いつつ浅くするのがいいか (2)フーリエを使わずにDilated Convで置き換えるのがいいのか は検討の余地がありそうです。
低解像度で訓練して高解像度で推論する試み
LaMaがこれまでのInpaintingと大きく異なるのが、「256pxのような低解像度で訓練し、512pxのような高解像度で推論しても性能が落ちにくい」という点です。LaMaはさらに拡張し、1536×1536まで行っています。
これまでのモデルだと、1536×1536のような大きい画像は、256×256の解像度のパッチを6×6個並べて各パッチについて推論を行うという方法でした。ところが、LaMaの場合はメモリが許す限りで、高解像度の画像を一気に入力に入れてもそこまで性能が落ちないということが示されています。最初から高解像度で訓練する必要はなく、低解像度で訓練しても性能が落ちにくいのです。
以下の図は、256×256で訓練したモデルに対し、640×512、1920×1536の画像をそれぞれ入力に与え、推論したの結果です。
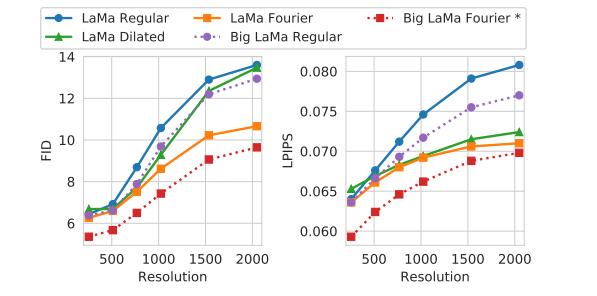
特に下(1920×1536)で、「LaMa-Regular」や「Big LaMa-Regular」のようなFFTやDilated Convを使わないケースで、もこっとした大きな欠損が確認できます。定量評価で見ると、
フーリエベースはFIDやLPIPSの両方で、DilatedベースはLPIPSで、推論解像度の上昇に対して性能劣化が遅いことが確認できます。FFCがよりロバストである理由について論文では、
- 画像全体の受容野を持つこと
- スケールが変わっても低周波のスペクトルは維持されること
- 周波数領域の1×1畳み込みに固有のスケール等変性があること
を理由として挙げています。
なお、Big LaMa-FourierはLaMa-Fourierをより大きくしたモデルです。Big LaMa-Fourierは18個のFFCを持つResidual Blockで、51Mのパラメーターを持ち、Placesデータセットの450万枚のサブセットで訓練しています。Big LaMa-Fourierは8個のV100GPUを使い、240時間訓練させたとのことです。通常のLaMa-Fourierの訓練時間は不明ですが、Big LaMa-Fourierでなく通常のLaMa-Fourierで、データ数を絞ればまあまあ現実的なモデルではないかと思います。
Big LaMaのうまくいく例・うまくいかない例
成功例
この論文、成功例だけでなく提案手法の失敗も書いてあるのが良いです。まずは成功例から。
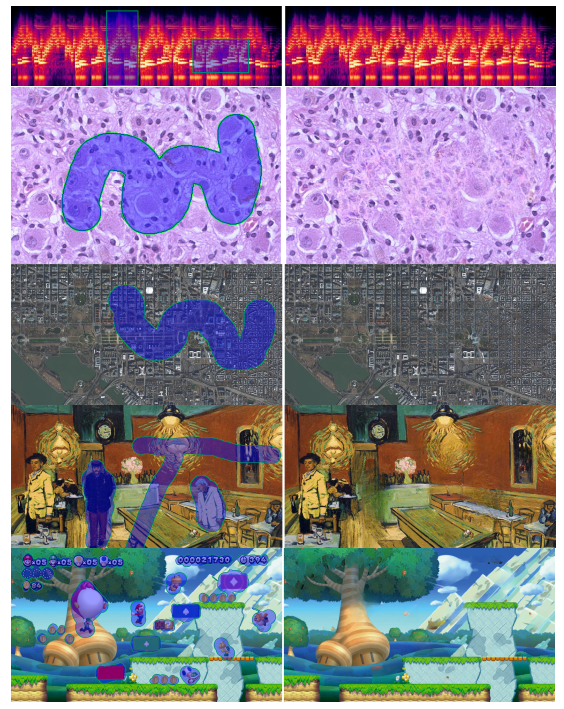
窓枠や屋根、格子模様に対する修復が強いですね。未知のドメインに対する修復にもある程度ロバスト性があります。
これはPlacesデータセットで訓練したもので、これらのドメイン画像は一切含まれていません。航空写真は厳しいかなという印象がありますが、個人的にすごいなと思ったのがマリオのゲーム画面で、ゲームの画像を一切見ないで修復できるのはすごいです。
失敗例
LaMaは遠近法の歪みや複雑な背景に対しては苦手とのことです。
まとめと感想
この論文はフーリエ変換と畳み込みを組み合わせて、グローバルな特徴を取得し、Inpaintingを適用するという内容でした。特に低解像度で訓練して、高解像度で推論してもそこまで性能が落ちないというのが素晴らしいです。大きい受容野を得るためには、フーリエ変換やDilated Convが唯一の方法ではなく、Vision Transformerも有効な選択肢だと述べています。
個人的に非常に面白く刺さる論文でした。Inpaintingは私が『モザイク除去から学ぶ最先端のディープラーニング』という本を書いていて、フーリエ変換による画像周波数特性の把握や、高周波帯の情報の活用が重要であるというのが体感的にわかっていました。それに対するほぼほぼ100%クリティカルな答えを出してきた研究が、このLaMaであると思います。格子や窓枠のように反復するパターンが難しいのは確かにそのとおりですし、Edge Connectに対して大差をつけるほどよいというのは驚かされました。高解像度への拡張は全くの予想外で「えっそんなことできるの」と食い入るように読んでしまいました。
論文読んでいて「FFTで広域特徴取れるなら、わざわざ実装のめんどくて重いSelf Attentionいらないやん」と思ったら、関連する研究1, 2であって、「なるほどー」と思わされました。個人的に言えばTransformerでゴリゴリやるよりも、FFTを挟んだConvNetが流行るのはわかりやすくていいかなーと思います。
論文の著者のスタンスは、InpaintingSoTAを叩き出したという主語の大きい議論よりかは、大きい受容野を持つInpaintingのモデルのためのベースラインを作ったよぐらいの位置づけです。個人的には謙虚でいいかなと思いました。
告知
このアドベントカレンダーが本になりました!
https://koshian2.booth.pm/items/3595424
Amazonでも扱いあります詳しくは👉 https://shikoan.com
-
フーリエ変換して畳み込みという誰かはやっていそうな内容なので、もっと古くからある論文かと思っていましたが、2020年とかなり最近の論文なので驚きました ↩
-
このようなLocal-Globalなモジュール構成はたびたび見られます。例えばOctConv(https://arxiv.org/abs/1904.05049) もこのケースです。OctConvの場合はFFTをせずに、ダウンサンプリングした画像を低周波、元の解像度の画像を高周波とし、このようなモジュール構成をしていました。畳み込みカーネルの性質上、低周波の場合はより広域な特徴を、高周波の場合はより局所的な特徴を捉えるので、OctConvもこのようなLocal-Globalなモジュール構成の一種とみなすことができます。事実、ダウンサンプリングがローパスフィルターであるので、FFTのように明示的に周波数分解をおこなくても発想は近いと考えられるでしょう。 ↩
-
論文表記の用語と異なっていて探すのに苦労しました。 ↩