Parametric t-SNEの理論とKerasによる実装

t-SNEといういい感じに次元削減してくれるアルゴリズムがありますが、これをKerasで行う例を紹介します。はじめにScikit-learnでのt-SNEを紹介し、parametric t-SNEが何をやっているのかを説明し、Kerasでの実装を紹介します。

Parmaetric t-SNEの実装はあっても理論の解説がほとんど見当たらなかったので、理論を中心に説明していきます。できるだけ丁寧に解説するようにしましたが、t-SNE自体は結構ハードな内容なので覚悟して読んでください。

コードは先人の実装をフォークして使いました。なので内部の実装はほとんど自分のものではありません¹。自分が論文読んで理解した範囲内でのt-SNEのアルゴリズムの説明を中心に行っていきます。説明ガバかったらマサカリ飛ばしていただけると幸いです。

元の論文と偉大なる先人

元の論文

Learning a Parametric Embedding by Preserving Local Structure
https://lvdmaaten.github.io/publications/papers/AISTATS_2009.pdf

Visualizing Data using t-SNE
https://lvdmaaten.github.io/publications/papers/JMLR_2008.pdf

上が今回実装するParametic t-SNEの論文で、下が元のt-SNEの論文です。どちらも同じ方（Laurens van der Maatenさん）が書いています。

偉大なる先人の実装

こちらの記事を参考にしました。

PARAMETRIC T-SNE を KERAS で書いた
https://zaburo-ch.github.io/post/parametric-tsne-keras/

同じ方の実装はgithubにあります（ただしPython2なのでPython3でやるときはコピペでは動きません）。この実装はt-SNEの作者による実装を若干改変したものだそうです。
https://github.com/zaburo-ch/Parametric-t-SNE-in-Keras

Scikit-learnでのt-SNE

t-SNEがどのような感じなのかざっくりと見るには、Scikit-learnで実行してみるのが早いです。

from keras.datasets import mnist
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt

def plot_sklearn_tsne():
    (X_train, y_train), (_, _) = mnist.load_data()
    X_train = (X_train / 255.0).reshape(-1, 784)
    tsne = TSNE(n_components=2)
    proj = tsne.fit_transform(X_train[:1000])
    cmp = plt.get_cmap("Set1")
    plt.figure()
    for i in range(10):
        select_flag = y_train[:1000] == i
        plt_latent = proj[select_flag, :]
        plt.scatter(plt_latent[:,0], plt_latent[:,1], color=cmp(i), marker=f"${i}$")
    plt.title("t-SNE")
    plt.show()

if __name__ == "__main__":
    plot_sklearn_tsne()

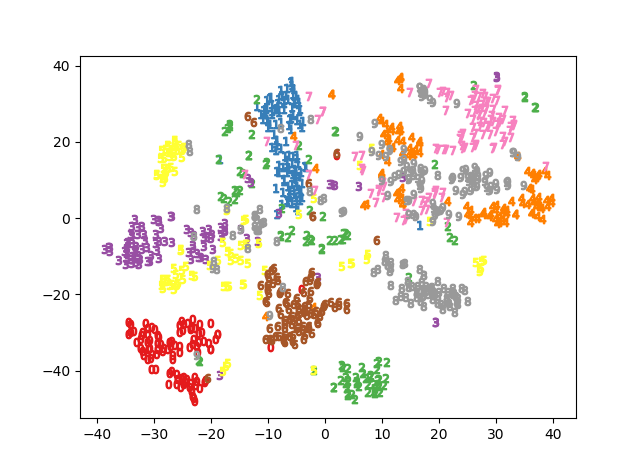
これはMNIST、1000サンプルのt-SNEを行ったものですが、数字ごとにエリアが密集していていい感じですね。Ground truthの値は後から与えたものですが、教師なしでここまでできるのはすごい。

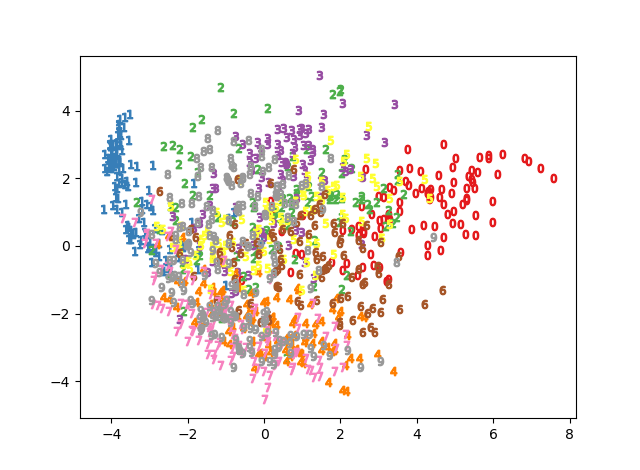
ちなみに主成分分析（PCA）で次元削減するともっと散漫な結果になります²。上のコードのTSNE()の部分をfrom sklearn.decomposition import PCAのPCA()に置き換えただけです。

t-SNEのほうが明らかにラベル同士で密なクラスタができているのが確認できます。

t-SNEのやっていること

「こんなに綺麗に次元削減できているt-SNEってどんなマジック使ってるの？」ということですが、やっていることはデータの空間のサンプル間の同時分布と、潜在空間のサンプル間の同時分布を取り、2つの分布を似せるようにする。具体的には同時分布同士のKLダイバージェンスの最小化を行っているということです。

これで理解できた方は天才です。まずは同時分布から説明していきます。知っているところは適宜飛ばしてくださいね。

条件付き確率と同時分布

t-SNEを理解するにあたっては、条件付き確率と同時確率（分布）の違いを知ることがまず大きな第一歩です。

条件付き確率の定義の式です。$P(B)\neq0$ですると、**BにおけるAの条件付き確率$P(A|B)$**は、

$$P(A|B)=\frac{P(A,B)}{P(B)} $$

で表されます。$P(A,B)$を$P(A\cap B)$を書くこともあります。ここで**$P(A,B)$をA,Bの同時確率**と呼びます。同時確率の分布を同時分布と呼びます。

具体例

「夕焼けが見れると次の日は晴れ」という言い伝えがあります³。**事象Aを「次の日晴れたかどうか」、事象Bを「前日に夕焼けが観測できたかどうか」**とします。この具体的なデータは見つけることができなかったのですが、以下の表のようなデータが取れたとしましょう。

A/B	前日に夕焼けが見れた（B=1)	前日に夕焼けが見れなかった（B=0)	合計
次の日晴れ（A=1）	0.4	0.1	0.5
次の日晴れない（A=0）	0.2	0.3	0.5
合計	0.6	0.4	1

実はこの表がA,Bの同時分布なのです。確率分布なので全体の合計が1になるようにします。

先程の式に合わせると、前日に夕焼けが見れて（B=1）かつ次の日に晴れだった（A=1）の確率（同時確率）は、
$$P(A=1, B=1)=0.4 $$
となります。では「前日に夕焼けだった（B=1）ときに、次の日が晴れる確率（A=1）」はどうなるのでしょうか？日本語で書くとややこしいですが、こちらは「条件付き確率」で、同時確率では次の日が晴れたということが観測できていますが、条件付き確率では次の日の天気はわかりません。したがって、雨が降る可能性も捨てきれません。条件付き確率の式に代入すると、

\begin{align}
P(A=1|B=1)&=\frac{P(A=1,B=1)}{P(B=1)} \\
 &=\frac{P(A=1,B=1)}{P(A=0,B=1)+P(A=1,B=1)} \\
 &=\frac{0.4}{0.2+0.4} \\
 &=\frac{2}{3} 
\end{align}

つまりこのデータの場合、「夕焼けが見れたら次の日は2/3の確率で晴れる」ということがいえます。直感的にはこの式は理解しやすいですが、かなりエッセンスがつまっています。多次元で何やってるんだかよくわからなくなったときはこの2次元の例を振り返ってください。
t-SNEでは特に意識することはないですが、$P(B)$を周辺確率呼びます。そして周辺確率は同時確率の和（連続分布なら積分）で表されます。ちょうど分母で「0.2+0.4」としているところがそうです。

では、「夕焼けが観測できなかったときにおける（B=0）、次の日に晴れない（A=0）」の条件付き確率$P(A=0|B=0)$と、同時確率$P(A=0, B=0)$はそれぞれいくつになるでしょうか？

答えはそれぞれ、$\frac{3}{4}=0.75, 0.3$です。なぜか理解できなかったら手計算で求めてみてください。条件付き確率と同時確率の違いがわからないとt-SNEを理解できないので。

Parametric t-SNEのアルゴリズム

1. 同時分布のKLダイバージェンスの最小化問題

データ$X$を与え、$Y$という潜在空間にマッピングするニューラルネットワークを考えます。$Y$はニューラルネットワークのモデルの出力層の値です。ニューラルネットワークの係数$W$が与えられたとき、ニューラルネットワーク全体を1つの関数とみなすと、

$$X\to Y \qquad X\to f(X|W) $$

というマッピングを行っているにほかなりません。今、データ$X$のサンプル間の同時分布の行列を$P$、ニューラルネットワークを通ったあとの潜在空間$Y$のサンプル間の同時分布の行列を$Q$とします。この同時分布の直感的な理解はサンプル間の距離のようなもの（類似度）なのですが、なぜ確率が距離として扱えるかは後で実際に確認します。今はそういうものだと思ってください。

Parametric t-SNEの損失関数は以下のように定義します⁴。

$$C=KL(P||Q)=\sum_{i\neq j}p_{ij}\log\frac{p_{ij}}{q_{ij}} $$

この式は$i\neq j$という制約があるものの、一般的なKLダイバージェンス（カルバック・ライブラー情報量）の定義ほかなりません。

KLダイバージェンスを本当に理解するのは難しいですが、Pythonで計算するのは全然難しくなくて、scipy.stats.entropy（ドキュメント）だったり、Kerasならkeras.objectives.kullback_leibler_divergence （ドキュメント）で一発で計算してくれます。大事なのは、2つの分布が完全に同一ならKLダイバージェンスは0になり最小値になるということです。2つの分布が異なれば異なるほど、KLダイバージェンスが大きくなります。平均二乗誤差と同じような感覚で使え、こちらは分布間の情報量の違いに焦点を当てた指標ぐらいの理解で十分だと思います。より直感的な理解だったらこちらの記事の図を見てください。

つまり、KLダイバージェンスの最小化とは、2つの分布がなるべく同じようにするということになります。Parametric t-SNEのやっていることとは、データ$X$の同時分布$P$と、潜在空間$Y$の同時分布$Q$を同じ分布になるようにするということです。潜在空間のほうが次元数が少ないので、少ない次元で同じ分布を再現できたら嬉しいですよね。このへんの発想は主成分分析に通じるものがあります（やっていることは主成分分析より相当複雑です）。

具体的に$P$と$Q$ってどうやって計算するの？というのはこれから説明します。

2. データXの同時分布P

もう少し概念的な説明が続きますがご辛抱ください。まずサンプル$x_i$が与えられたときの、サンプルの$x_j$の**条件付き確率を$p_{j|i}$**とします。いきなり同時分布にはいきません。$p_{j|i}$は次の式で定義します。

$$p_{j|i}=\frac{\exp(-||x_i-x_j||^2/2\sigma_i^2)}{\sum_{k\neq i}\exp(-||x_i-x_k||^2/2\sigma_i^2)} $$

また、$i=j$のとき、つまり$p_{i|i}=0$とします。今$x_i$はベクトルになりますから、$||x_i-x_j||$はベクトルのノルムになります。ノルムはサンプル同士の距離$(x_{i,1}-x_{j,1})^2+(x_{i,2}-x_{j,2})^2\cdots$を求めており、最も基本的なユークリッド距離で表されます。もし$x_i$の次元が1なら、ノルムをただの括弧の2乗に置き換えても構いません。

ところで、$p_{j|i}$の分子を見ると、正規分布の式であることに気づきます。より正しく言えば、平均が$x_i$⁵、分散が$\sigma_i^2$の正規分布です。1変数の正規分布の確率密度関数は、

$$f(x)= \frac{1}{\sqrt{2\pi\sigma^2}}\exp\bigl(-\frac{(x-\mu)^2}{2\sigma^2}\bigr)$$

で表されますからね。分子分母が正規分布なら係数は消えてしまいますので。

今簡単な例として、データの次元を1次元として、$X=(1,2,3)$としましょう。そして$z_j=\exp(-(x_i-x_j)^2/2\sigma_i^2)$とおきます。すると条件付き確率$p_{j|i}$は次のような行列になります。

\begin{bmatrix}
0 & \frac{z_2}{z_2+z_3} & \frac{z_3}{z_2+z_3} \\
\frac{z_1}{z_1+z_3} & 0 & \frac{z_3}{z_1+z_3} \\
\frac{z_1}{z_1+z_2} & \frac{z_2}{z_1+z_2} & 0
\end{bmatrix}

この行列は後ほどプログラムで確認しますが、正規分布の確率密度関数はxが大きくなればなるほど値が小さくなります。例えば$x_i=x_1=1$のときの、$x_j=x_2=2$に対する$z_2$と、$x_j=x_3=3$に対する$z_3$を比べると、$z_2>z_3$になります。しかも指数関数的に減少します。つまり、サンプル間の差が小さいほど、条件付き確率は大きくなるということになります。これは条件付き確率を距離として使うことができるということを表します。確率が距離扱いになるというのはこういう理由です。

今条件付き確率$p_{j|i}$のみ定義しましたが、同時確率$p_{ij}$を条件付き確率を使って次のように定義します。

$$p_{ij}=\frac{p_{j|i}+p_{i|j}}{2n} $$

$p_{ij}$の直感的な解釈はデータiとjの類似度（これはParametric t-SNEの論文による）となります。この定義により同時分布の行列$P$が直交化されます⁶。

ちなみに、特に断りもなく分散$\sigma_i^2$が求められるように書きましたが、実際は**「Perplexity」という指標を導入して、サンプル間のPerplexityが同一になるように$\sigma_i^2$を最適化（二分探索）して求める**という結構回りくどいことをします。これは、t-SNE特有の次元削減後の密な集合を表現するために必要なものです。

Perplexityの計算方法は次のようにします。これはParametric t-SNEの論文ではなく、大元のt-SNEの論文に書かれていました。まず、条件付き確率$p_{j|i}$から**シャノンエントロピー$H(P_i)$**を計算します。

$$H(P_i) = -\sum_{j}p_{j|i}\log_2 p_{j|i} $$

次にシャノンエントロピーのべき乗を取ります。これがPerplexityです。

$$Perp(P_i)=2^{H(P_i)} $$

そして、$i$ごとのPerplexityが一定（Parametric t-SNEでは30）になるように、条件付き確率$p_{j|i}$の内側の対応する$\sigma_i^2$を決めます。この探索には二分探索を使います。

3. 潜在空間Yの同時分布Q

正直数式ばっかりでげっそりしてきますが、これで終わりです。最後にニューラルネットワークの出力層（潜在空間）の$Y$の同時分布$Q$を定義します。こちらは条件付き確率ではなく、同時分布$q_{ij}$をダイレクトに定義します。

$$q_{ij}=\frac{(1+||f(x_i|W)-f(x_j|W)||^2/\alpha)^{-\frac{\alpha+1}{2}}}{\sum_{k\neq l}(1+||f(x_i|W)-f(x_j|W)||^2/\alpha)^{-\frac{\alpha+1}{2}}} $$

なんかクラクラしそうな式ですが、$f(x_i|W)$は$x_i$をニューラルネットワークに通した後の値であることを思い出しましょう。そう考えると$p_{j|i}$の式とあまり変わらないように見えます。なお$\alpha$は何種類か置き方がありますが、潜在空間の**次元$d-1$**で定義するのが自然です⁷。

「$P$と$Q$なぜ違う分布で定義するんだ？同じ分布でいいんじゃないか？」という疑問は確かにあります。ちなみに**$P$は正規分布、$Q$はt分布**で定義しています。

t分布にはαを大きくして極限を取ると正規分布に収束するという性質があります（これを説明するとえらい数式が増えるので気になる方はこちらをご覧ください）。詳しい説明は省きますが、$Q$を正規分布でやると特定の条件でサンプルが密集した結果になってしまうそうです（Crowding Problem）。「潜在空間の次元はデータのよりも低次元になっているから、正規分布よりもt分布を使うほうが適切」ぐらいでも、直感的に理解するには十分そうです。

ちなみに元のt-SNEの論文を見ると、$Q$を正規分布で考えているケースもあります。これを**SNE（Stochastic Neighbor Embedding）**といいます。つまり、t-SNEとはSNEの$Q$をt分布に変えたというわけです。t分布に変えるとCrowding Problemが緩和されるとのことです。

これでParametric t-SNEを構成するパーツが全て揃いました。もう一度おさらいすると、「Parametric t-SNEはデータの同時分布$P$と潜在空間の同時分布$Q$を同一化させようとする、具体的には$P,Q$のKLダイバージェンスを損失関数として、これを最小化させるようにニューラルネットワークを訓練する」です。

最後になぜこれが「Parametric」と呼ばれるかですが、おそらくこれは統計学のパラメトリック、ノンパラメトリックの文脈に由来すると思います。統計学におけるパラメトリックとは、データに対して分布の仮定をおくものです。Parametric t-SNEでは、データに対して正規分布、潜在空間に対してt分布という仮定を置いているため、このことをもってパラメトリックと呼ばれるのでしょう。

Parametric t-SNEの同時確率を試す

条件付き確率の解釈

正直数式ばっかりで理解しづらいので、簡単な例をPythonで試してみます。条件付き確率$p_{i|j}$の式は以下の通りでした。

$$p_{j|i}=\frac{\exp(-||x_i-x_j||^2/2\sigma_i^2)}{\sum_{k\neq i}\exp(-||x_i-x_k||^2/2\sigma_i^2)} $$

また同時分布$P$の要素である、同時確率$p_{ij}$は以下のようになります。

$$p_{ij}=\frac{p_{j|i}+p_{i|j}}{2n} $$

これをバカ正直にPythonのコードで書くと以下のようになります。

import numpy as np

def calc_P_fix_sigma(X, sigma_sq):
    assert X.ndim == 2
    n = len(X)

    # 距離
    D = np.zeros((n,n))
    # 条件付き確率
    Pcond = np.zeros(D.shape)
    # シャノンエントロピー
    H = np.zeros(n)

    for i in range(n):
        # 距離の計算
        for j in range(n):
            # 本来はsigma_sqは探索で求めるが、既知のものとする
            D[i,j]=np.exp(-np.sum((X[i,:]-X[j,:])**2, axis=-1) / (2*sigma_sq))

        # 条件付き確率の計算
        for j in range(n):
            if i==j: continue
            tmp = 0
            for k in range(n):
                if i==k: continue
                tmp += D[i,k]
            # p j|i
            Pcond[i,j] = D[i,j] / tmp

        # シャノンエントロピーの計算
        tmp = 0
        for j in range(n):
            if i==j: continue
            tmp += Pcond[i,j] * np.log2(Pcond[i,j])
        H[i] = -tmp

    # perplexity＝クラスタの大きさ
    perp = np.power(2.0, H)
    # perplexityとsigma_sqは正の関係がある
    # perplexityはsigma_sqを大きくすると最終的にn-1になる
    # 実際はperp[i]を固定して、それを満たすようなsigma_sqを探す

    # 同時確率
    Pjoint = np.zeros(D.shape)
    for i in range(n):
        for j in range(n):
            Pjoint[i,j] = (Pcond[i,j]+Pcond[j,i]) / 2 / n

    print("条件付き確率")
    print(Pcond)
    print("同時確率")
    print(Pjoint)
    print("perplexity")
    print(perp)

$\sigma_i^2$は本来perplexityから探索により求めますが、今わかりやすいように$\sigma_i^2$が既知のものとします。$X=[1,2,3], \sigma_i^2=1$のときの結果は次のようになります。

if __name__ == "__main__":
    X = np.array([1,2,3]).reshape(-1,1)
    calc_P_fix_sigma(X, 1)

X=[1,2,3]の場合

条件付き確率
[[0.         0.81757448 0.18242552]
 [0.5        0.         0.5       ]
 [0.18242552 0.81757448 0.        ]]
同時確率
[[0.         0.21959575 0.06080851]
 [0.21959575 0.         0.21959575]
 [0.06080851 0.21959575 0.        ]]
perplexity
[1.60809711 2.         1.60809711]

なんとなく確率が距離として扱えることがわかってきたでしょうか？条件付き確率の1行目は、i=1が与えられたときのjの値ごとの条件付き確率の分布です。$x_i=1$なので、$x_3=3$よりも$x_2=2$のほうが出る確率が高い、2を選んだほうがよりもっともらしい⁸、ということを表します。逆に2行目はi=2が与えられたときの条件付き確率なので、1を選ぼうが3を選ぼうがもっともらしさは同じということになります。3行目は1行目の逆ですよね。

では$X=[1,2,4]$だったらどうでしょうか？i=1のときの条件付き確率は、2を選ぶほうにより集中するはずです。

X=[1,2,4]の場合

条件付き確率
[[0.         0.98201379 0.01798621]
 [0.81757448 0.         0.18242552]
 [0.07585818 0.92414182 0.        ]]

この通り。i=2のときの条件付き確率も対称ではなくなり、すでに選ばれた2より遠い4よりも、2に近い1のほうが選ばれる確率のほうが高くなるようになります。これはとても自然な結果です。ちなみに対角要素は、i=1を選んだときにまたj=1が選ばれるということなので、定義しなくてよい、つまり0と置いてよいのです。

また、同時確率は全ての要素の合計が1であることを確認してください。これは確率分布の要件を満たすために必要です。条件付き確率の各行の合計が1なので、それを同時確率の定義の分子ぶん足すと合計は$2n$、分母も同じく$2n$で割っているので、同時確率の合計は必ず1になります。

同時分布のKLダイバージェンスの直感的な解釈

本来はt-SNEはPを正規分布、Qをt分布でやりますが、今わかりやすいようにPもQも正規分布、つまり普通のSNEで行うものとします。

先程のコードはバカ正直にforループで書きましたが、ご存知の通りこういう計算は行列で書くべきなのでもうちょっと賢く書きました。まずX_to_affinitiesでXを距離に（難しい言葉でいうとアフィンに）変換し、これをキャッシュさせます。このキャッシュは、今は$\sigma_i^2$を既知のものとしているので（perplexityの統一をしていない）特に必要ありませんが、本来の$\sigma_i^2$を既知のものとしない、つまりperplexityの統一を行う際に必要な二分探索を高速化するために使います。

# ベクトル版
def X_to_affinities(X):
    # 距離のsigma_sqで割らない部分を先に計算
    gramX = np.dot(X, X.T) # グラム行列をとり(N,N)にする
    # ||xi - xj||^2 = ||xi||^2 - 2xixj + ||xj||^2
    Xi_sq = np.sum(X**2, axis=-1).reshape(-1, 1)
    xj_sq = np.sum(X**2, axis=-1).reshape(1, -1)
    affinities = Xi_sq + xj_sq - 2*gramX
    return affinities

def affinities_to_perp(affnities, i, sigma_sq):
    assert affnities.ndim == 2
    n = affnities.shape[0]
    assert i >= 0 and i < n
    eps = 1e-14

    # 距離の計算
    # D=np.exp(-np.sum((X[i:i+1,:]-X)**2, axis=-1) / (2*sigma_sq)) だから
    # np.sum(…)をaffinitiesとすれば、
    # D = np.power(np.exp(-affinities[i]), 1/(2*sigma_sq)) すれば高速に計算できる（アフィンのキャッシュ）
    D = np.power(np.exp(-affnities[i]), 1/(2*sigma_sq))

    # 条件付き確率の計算
    # i≠kの和
    flag = np.ones(n)
    flag[i] = 0
    d_sum = np.sum(D*flag)
    # Pcondの対角成分も0にする
    Pcond = D / (d_sum+eps) # 0割り対策
    Pcond[i] = 0

    # シャノンエントロピーの計算
    H = -np.sum(Pcond * np.log2(Pcond+eps)) # log0対策
    # perplexity
    perp = np.power(2.0, H)
    return Pcond, perp

def calc_P_fix_sigma_vectorized(X, sigma_sq):
    assert X.ndim == 2
    n = len(X)

    Pcond = np.zeros((n,n))
    perp = np.zeros(n)
    affinites = X_to_affinities(X)

    for i in range(n):
        Pcond[i,:], perp[i] = affinities_to_perp(affinites, i, sigma_sq)

    print(Pcond)
    print(perp)

    return Pcond

from scipy.stats import entropy

def eval_entropies(P, Q):
    print("KLダイバージェンス")
    print(entropy(P, Q))

if __name__ == "__main__":
    X = np.array([1,2,3]).reshape(-1,1)
    print("P")
    P = calc_P_fix_sigma_vectorized(X, 1.0)
    Y = np.array([-3,-2,-1]).reshape(-1,1)
    print("Q（正規分布とする）")
    Q = calc_P_fix_sigma_vectorized(Y, 1.0)
    eval_entropies(P, Q)

今ニューラルネットワークを通って、$X=[1,2,3]$が$Y=[-3,-2,-1]$に変換されたものとします。XとYの同時分布P,Qを求め、KLダイバージェンスを計算してみましょう。繰り返しますが、今Qは正規分布で計算していますが、Qの分布はt-SNEではt分布を使います。

X=[1,2,3]→Y=[-3,-2,-1]の場合

P
[[0.         0.81757448 0.18242552]
 [0.5        0.         0.5       ]
 [0.18242552 0.81757448 0.        ]]
[1.60809711 2.         1.60809711]
Q（正規分布とする）
[[0.         0.81757448 0.18242552]
 [0.5        0.         0.5       ]
 [0.18242552 0.81757448 0.        ]]
[1.60809711 2.         1.60809711]
KLダイバージェンス
[0. 0. 0.]

P,Qごとに条件付き確率、Perplexityの順です。

KLダイバージェンスが0ということは、2つの分布が全く同一ということなので、この2つの分布は同一であるということがわかりました。それはそうです。Xを-4だけずらしたのがYなのですから。ではもし$Y=[-3,-2,10]$だったらどうでしょう？

Q（正規分布とする）
[[0.00000000e+00 1.00000000e+00 3.30570063e-37]
 [1.00000000e+00 0.00000000e+00 8.87042736e-32]
 [2.00500878e-23 5.38018616e-18 0.00000000e+00]]
[1. 1. 1.]
KLダイバージェンス
[13.39055126 19.18875717  2.76092087]

このように非常に大きなKLダイバージェンスが観測されました。確かに、1→-3、2→-2というマッピングをしておいて、3だけいきなり10にマッピングするというのはおかしいです。PとQが同一の分布とはとても言えません。PとQのKLダイバージェンスの最小化を行う(t-)SNEの観点ではこのマッピングは間違っています。

では**$Y=[5,10,15]$だったら**どうでしょう？これはただ5倍しただけなので直感的にはそこまでおかしくないマッピングです。

X=[1,2,3]→Y=[5,10,15]の場合（Pは同一なので省略）

Q（正規分布とする）
[[0.00000000e+00 9.99999997e-01 5.17555499e-17]
 [4.99999999e-01 0.00000000e+00 4.99999999e-01]
 [5.17555499e-17 9.99999997e-01 0.00000000e+00]]
[1. 2. 1.]
KLダイバージェンス
[9.25860839 0.         9.25860839]

このようにKLダイバージェンスは大きくなりました。つまり、(t-)SNEでは元の変数を定数倍するような距離（アフィン）の変換は、同一の分布とみなさないということになります。

逆に言えば、(t-)SNEを使う限りにおいては、スケールを定数倍して伸び縮みさせるようなマッピングはしないということになります。伸び縮みするような変換はKLダイバージェンスの尺度により「異なる分布」であるとみなされます。これはつまり、前の隠れ層でどのような値が返ってきても、マッピング先ではある一定のスケールに収まるようにニューラルネットワークが最適化されていくことを示します。したがって、Parametric t-SNEではニューラルネットワークで隠れ層の特徴量を取るときに使うようなtanhやシグモイドの活性化関数はいらなくなります。Parametric t-SNEでは出力層に活性化関数を使う必要はありません。

まとめると、t-SNEでは同時分布P,QのKLダイバージェンスを取っていますが、裏でやっていることはデータや潜在空間の値をアフィンを経由して、相対化させた形で分布の比較を行っている。ということになります。

Perplexityとはなにか、その探し方とは？

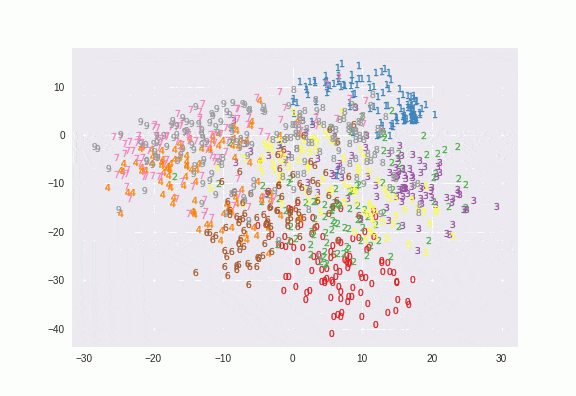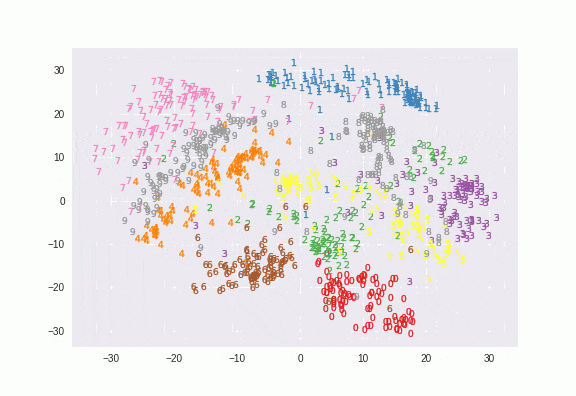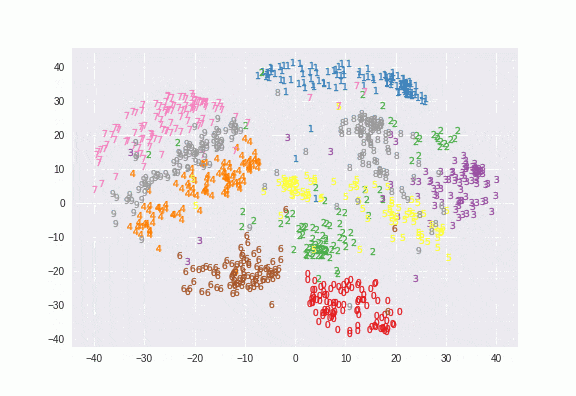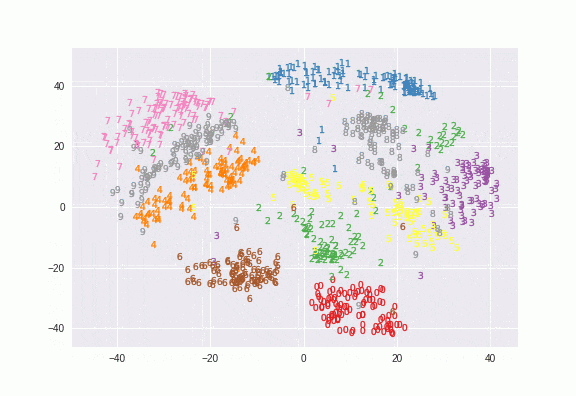
今まで$\sigma_i^2$が既知のものとして、Perplexityにはほとんど触れませんでしたが、ここの説明をしておきましょう。Perplexityとは1つのサンプルについて近傍をどれだけ考えるか平滑化の値、よりざっくり言えばクラスタの大きさです。Perplexityが高いほど、1つのクラスタが大きくなり、データ全体が1つの塊とみなされより、漫然としたプロットとなります。逆にPerplexityが低いほど、1つのクラスタが小さくなり、より密な状態でプロットされます。

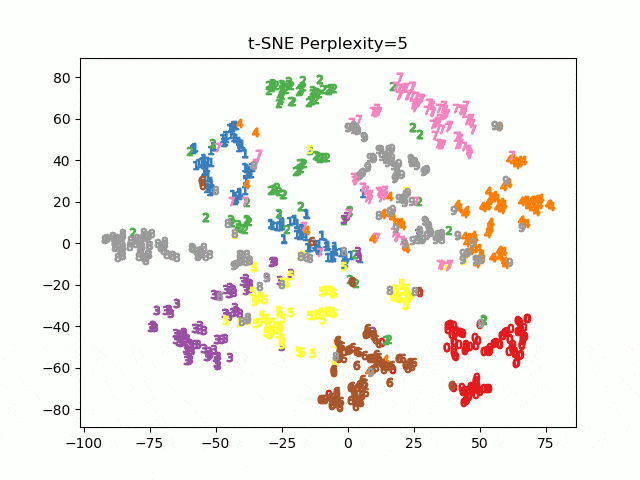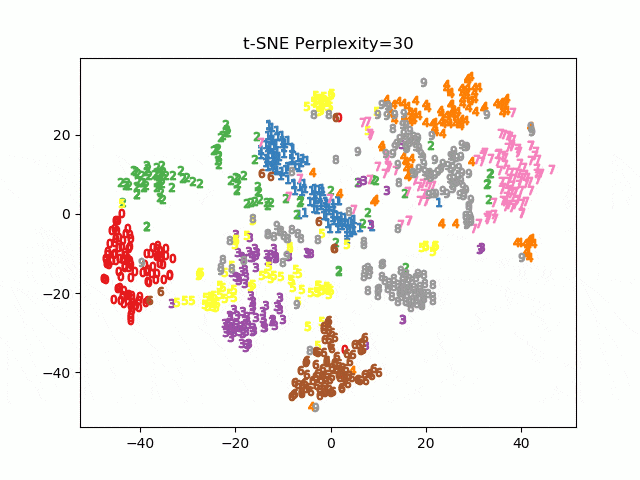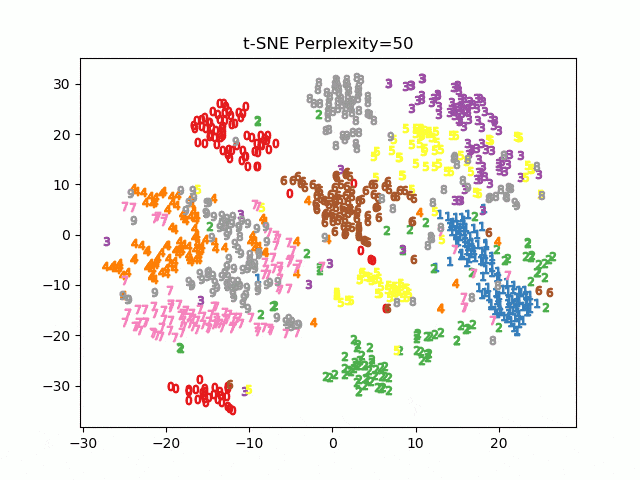
今SklearnでPerplexityの値を5,30,50の3パターンをプロットさせました。これで違いがわかると思います。

Perplexityが5のほうが締まりがよくて、50だとかなりぼやけたプロットになっていますよね。Perplexityは5～50が良いとされ、Parametric t-SNEでは30を使っています。特にこの値は変更しませんが、クラスタリング用途だと重要なパラメーターになるはずです。

Perplexityと$\sigma_i^2$には正の関係があり、$\sigma_i^2$が大きくなればなるほどPerplexityは大きくなります。また、Perplexityは最終的にサンプルの数N-1に収束します⁹。この関係を確認してみましょう。

def eval_perplexity(X):
    print("sigma=0.5の場合")
    calc_P_fix_sigma_vectorized(X,0.5)
    print("sigma=1の場合")
    calc_P_fix_sigma_vectorized(X,1)
    print("sigma=2の場合")
    calc_P_fix_sigma_vectorized(X,2)
    print("sigma=10の場合")
    calc_P_fix_sigma_vectorized(X,10)

if __name__ == "__main__":
    X = np.array([1,2,3,4]).reshape(-1,1)
    eval_perplexity(X)

$X=[1,2,3,4]$としました。$\sigma_i^2$を0.5、1、2、10と変えてPerplexityの値の変化を見ます。

PerplexityとSigmaの関係

sigma=0.5の場合
[[0.00000000e+00 9.52269826e-01 4.74107229e-02 3.19450938e-04]
 [4.87855551e-01 0.00000000e+00 4.87855551e-01 2.42888977e-02]
 [2.42888977e-02 4.87855551e-01 0.00000000e+00 4.87855551e-01]
 [3.19450938e-04 4.74107229e-02 9.52269826e-01 0.00000000e+00]]
[1.21372559 2.20472462 2.20472462 1.21372559]
sigma=1の場合
[[0.         0.80551241 0.17973411 0.01475347]
 [0.44981622 0.         0.44981622 0.10036756]
 [0.10036756 0.44981622 0.         0.44981622]
 [0.01475347 0.17973411 0.80551241 0.        ]]
[1.72442168 2.58433322 2.58433322 1.72442168]
sigma=2の場合
[[0.         0.62200588 0.29381477 0.08417934]
 [0.40447077 0.         0.40447077 0.19105846]
 [0.19105846 0.40447077 0.         0.40447077]
 [0.08417934 0.29381477 0.62200588 0.        ]]
[2.37150671 2.85328128 2.85328128 2.37150671]
sigma=10の場合
[[0.         0.39509638 0.3400626  0.26484102]
 [0.34956382 0.         0.34956382 0.30087237]
 [0.30087237 0.34956382 0.         0.34956382]
 [0.26484102 0.3400626  0.39509638 0.        ]]
[2.96113118 2.99277184 2.99277184 2.96113118]

上が条件付き確率、下がPerplexityです。Perplexityと$\sigma_i^2$と正の関係があることが確認できました。$\sigma_i^2$が大きくなるほど条件付き確率がバラけていくので、1つの大きな塊に食われていく、結果的に漫然としたプロットになるのが理解できるでしょう。

実際は$\sigma_i^2$が既知ではなく、Perplexityが既知でPerplexityが一定になるような$\sigma_i^2$を二分探索で計算して、条件付き確率→同時分布Pの順で計算します。二分探索はちょうどSklearnのt-SNEで使っている関数があるので（sklearn.manifold._utils._binary_search_perplexity()）、これを説明のために用います¹⁰。

from sklearn.manifold import _utils

# sigma^2の探索
def find_sigma(X, target_perplexity):
    # 条件付き確率を求める
    affinites = X_to_affinities(X).astype(np.float32)
    Pcond = _utils._binary_search_perplexity(affinites, None, target_perplexity, 1)
    # Perplexityの確認
    eps = 1e-14
    H = -np.sum(Pcond * np.log2(Pcond+eps), axis=-1)
    perp = np.power(2.0, H)
    print(Pcond)
    print(perp)

if __name__ == "__main__":
    X = np.array([1,2,3,4]).reshape(-1,1)
    #eval_perplexity(X)
    find_sigma(X, 2)

$X=[1,2,3,4]$に対して、Perplexityが2になるように条件付き確率を求めます。そして条件付き確率からPerplexityを再計算して本当に2になっているか確認します。

Perplexityの確認

[t-SNE] Computed conditional probabilities for sample 4 / 4
[t-SNE] Mean sigma: 0.488693
[[0.00000000e+00 7.27181120e-01 2.36459691e-01 3.63592281e-02]
 [5.00000006e-01 0.00000000e+00 5.00000006e-01 1.88756729e-11]
 [1.88756729e-11 5.00000006e-01 0.00000000e+00 5.00000006e-01]
 [3.63592281e-02 2.36459691e-01 7.27181120e-01 0.00000000e+00]]
[1.99998635 1.99999999 1.99999999 1.99998635]

OKですね。上が条件付き確率、下がPerplexityです。

これでようやくt-SNEの全貌を理解することができました。長かったですね。

Kerasで試してみる

偉大なる先人の知恵にあやかってこちらのリポジトリをフォークして使います。下手に実装するよりこちらのリポジトリのほうが速いです¹⁰。

フォークしたリポジトリがこちら。
https://github.com/koshian2/Parametric-t-SNE-in-Keras

tsne.pyにTSNE用の関数を詰め込みました。論文に載っていたMNISTのコードは以下のようになります。フォーク元のリポジトリにもありますが、Python3にしてジェネレータを自作するような形にしました。

from keras.layers import Dense, Input
from keras.models import Model
from keras.datasets import mnist
from keras.callbacks import Callback
import os, shutil, zipfile, glob
import matplotlib.pyplot as plt

from tsne import TSNE

import numpy as np

def create_model():
    input = Input((784,))
    x = Dense(500, activation="relu")(input)
    x = Dense(500, activation="relu")(x)
    x = Dense(2000, activation="relu")(x)
    x = Dense(2)(x) # 活性化関数はなし

    model = Model(input, x)
    return model


class Sampling(Callback):
    def __init__(self, model, X, y):
        self.X = (X / 255.0).reshape(X.shape[0], -1)
        self.y = np.ravel(y)
        self.model = model

    def on_train_begin(self, logs):
        if os.path.exists("plots"):
            shutil.rmtree("plots")
        os.mkdir("plots")

    def on_epoch_end(self, epoch, logs):
        latent = self.model.predict(self.X)
        cmp = plt.get_cmap("Set1")
        plt.figure()
        for i in range(10):
            select_flag = self.y == i
            plt_latent = latent[select_flag, :]
            plt.scatter(plt_latent[:,0], plt_latent[:,1], color=cmp(i), marker=f"${i}$")
        plt.savefig(f"plots/epochs{epoch:02}.png")

def generator(data_X, batch_size=5000):
    if data_X.ndim == 3:
        dims = data_X.shape[1] * data_X.shape[2]
    elif data_X.ndim == 4:
        dims = data_X.shape[1] * data_X.shape[2] * data_X.shape[3]

    while True:
        indices = np.arange(data_X.shape[0])
        np.random.shuffle(indices)
        for i in range(data_X.shape[0]//batch_size):
            current_indices = indices[i*batch_size:(i+1)*batch_size]
            X_batch = (data_X[current_indices] / 255.0).reshape(-1, dims)
            # X to P
            P = TSNE.calculate_P(X_batch)
            yield X_batch, P

def train():
    (X_train, y_train), (_, _) = mnist.load_data()

    model = create_model()
    model.compile("adam", loss=TSNE.KLdivergence)

    cb = Sampling(model, X_train[:1000], y_train[:1000])
    model.fit_generator(generator(X_train), steps_per_epoch=X_train.shape[0]//5000,
                        epochs=20, callbacks=[cb])

    files = glob.glob("plots/*")
    with zipfile.ZipFile("plots.zip", "w") as zip:
        for f in files:
            zip.write(f)


if __name__ == "__main__":
    train()

githubにも上げています。ポイントはジェネレーターの部分です。普通の教師あり学習では、Xにデータをyにラベルを与えますが、t-SNEではyの部分にXから計算した同時分布Pを与えます。そしてQは損失関数の中でテンソル演算でとして計算し、そのあとKLダイバージェンスを比較します。そこらへん気になる方はtsne.pyのほうを見てください。

ColabのGPUインスタンスでだいたい1エポック3分半ぐらい、20エポックで1時間ちょいかかりますね。ニューラルネットワークの訓練自体はほんの数秒でできます。とにかく二分探索の部分のCPUの計算量が多いので、GPUよりもCPUをいっぱい積んでいるケースのほうが速いはずです。

（二分探索を例えばニュートン法とか置き換えると速さはましになりそうだけど、そもそもPerplexityの微分ってどう計算するんだろう？）

訓練過程を可視化すると次の通りです。

教師なしでここまでできるのは素晴らしい。ニューラルネットワークの教師なしの例はあまり聞かないので、これは珍しい例かもしれません。

これのどこがすごいの？

ちなみにSklearnのt-SNEでMNISTを2次元に投射するとCPUで1分もかからずに出てきます。しかし、この方法だとGPU＋CPUで1時間もかかってしまいます。なら「ディープラーニングを使ったParametric t-SNEなんていらないのでは？」と言いたくなりますが、せっかくなので擁護しておきましょう。

1.任意の次元に投射できる

Scikit-learnのt-SNEは高速に計算するためにアルゴリズムが工夫されていますが、これには次元の制約があります¹¹。ここの記事で紹介した本当のt-SNEの計算量は$O(N^2)$ですが、Scikit-learnでは$O(NlogN)$で探索できるアルゴリズムをデフォルトで使っています。ただしこの高速化は精度¹²と次元の制約によるトレードオフで、4次元以上に投射するときは高速化ができません。例えばSklearnで16次元への投射をやろうとすると怒られます。

from sklearn.manifold import TSNE
from keras.datasets import mnist

(X, _), (_, _) = mnist.load_data()
X = (X / 255.0).reshape(-1,784)

tsne = TSNE(16).fit_transform(X)
#    raise ValueError("'n_components' should be inferior to 4 for the "
#ValueError: 'n_components' should be inferior to 4 for the barnes_hut algorithm
#as it relies on quad-tree or oct-tree.

エラー自体は低速のアルゴリズムにすれば消えるのですが、$O(NlogN)\to O(N^2)$になるので、高速化を切るとおそらくディープラーニングのアプローチのほうが速いというケースも往々にしてあるはずです。

2.End-to-Endなアプローチができる

今回はt-SNEだけやって終わりでしたが、このt-SNEを例えばImageNetで訓練したモデルで出てきた特徴量につけたり、AutoEncoderの特徴量につけたりディープラーニングとのEnd-to-Endなアプローチに適用することができます。今回はスペース都合でやりませんが、これはまた別の機会に見ていければなと思います。

3.ディープラーニングによるクラスタリングへのブレイクスルー

Perplexityの理解のところでも見ましたが、この値を変えるとクラスタリングとしても使えます。実際、ニューラルネットワークによるクラスタリング手法であるDeep Embedded Clusteringはt-SNEをもとにして作っているそうです。

まとめ

非常にハードでしんどい（読んでる側だけじゃなくて書いてる側もしんどい）内容となってしまいましたが、KerasでParametric t-SNEを動かすことができました。

Parametric t-SNEの理論としては、「データの空間のサンプル間の同時分布と、潜在空間のサンプル間の同時分布を取り、2つの分布を似せるようにする。具体的には同時分布同士のKLダイバージェンスの最小化を行っている」という点を抑えておけばOKです。

ディープラーニングなのに、GPUパワーよりもCPUパワーのほうが必要というちょっと変わった例でしたが、環境によっては使いこなせるのではないでしょうか。

1. フォークしたリポジトリは、もともとt-SNEの作者による実装を若干改変したものだったそうです。自分で1から実装したらあまりに下手くそで遅い・正しく動かないの存在価値なしコンボだったのでこちらを使います。 ↩

2. 非常に細かい話ですが、今回は主成分分析（t-SNEでも）標準化はしていません。「可視化なら標準化すべきでは？」というのは確かに正しいですが、今回は画像で全ての系列が同じピクセル値なので、標準化せずに同一のスケールで見ても悪くはないのではないでしょうか。もちろん標準化してもOKだと思います。 ↩

3. 季節によりけりですが、これは天気が西側から天気が変わることを意味していて、科学的根拠はある言い伝えだそうです。　https://www.jma-net.go.jp/akita/Q&A/qandanew_12.htm ↩

4. ちなみにPとQの行列の次元は一緒になります。これはサンプル間で距離（同時確率）を取るためです。ちょうどSVMに見られるようなカーネル法の発想を使います。 ↩

5. 今$i$が条件付き確率で与えられているので、$j$が変数になります。2乗しているので括弧内にマイナスを掛けても変わりません。 ↩

6. イメージ的には正規分布のカーネルの入った分散共分散行列や相関行列に近いのかも？ ↩

7. 論文では定数（α＝1）、線形（α＝d-1）、学習させるの3ケースがありました。今回は線形のケースです。 ↩

8. ここでの「もっともらしい」というのは実は統計学における「尤度」そのものです。なぜなら尤度関数は条件付き確率により定義されるからです。　https://ja.wikipedia.org/wiki/%E5%B0%A4%E5%BA%A6%E9%96%A2%E6%95%B0 ↩

9. 1つのクラスタがサンプル全体を囲むようになるイメージです。ここでは点同士の差、つまり距離を取っているのでN-1となります。 ↩

10. Perplexityの二分探索は、Sklearnよりの実装よりもフォークした先人の方の実装のほうが速くて正確なようです。二分探索はCPUで計算しないといけなく、KerasでGPU使ってもこの二分探索がだいたい（めちゃくちゃ）ボトルネックになります。Skelarnの実装だと1エポック300秒、これがフォーク元の実装だと200秒になります。あとSkelarnの実装はPerplexityの誤差が大きくなることもあるようで、自分がKerasで動かしたところロスが減っていかないという現象が確認できました。もしかしたら自分の実装がおかしいだけなのかもしれないので、Sklearnの実装が良くないのかはよくわかりません。しかし、フォーク元の実装ではうまくいきます。 ↩ ↩²

11. t-SNEが2,3次元ぐらいしかうまくいかないと語られることがありますが、これはt-SNEが良くないのではなくて、この高速に計算できるbarnes_hutアルゴリズムが3次元までしか使えないという点が大きいのだと思います。t-SNE自体はもう少し高い次元までロバスト性はあると思います（違っていたらすみません）。 ↩

12. ざっとソースを読んでみたところ、全体の同時確率を計算するのでなくて、近傍の周辺のみの同時確率を計算するそうです。高速には計算できるものの、かなり端折った上での計算方法であることは間違いありません。 ↩