機械学習？ディープラーニング？知識不要！TensorFlow/Kerasのパワーを最も簡単に体感する方法 #Python

皆さん機械学習やってますか？「テンソル？統計？線形代数？なにそれ美味しいの」って敬遠している方も多いのではないでしょうか。

今回は機械学習・ディープラーニングの知識一切なしで、ディープラーニングのフレームワークであるTensorFlow/Kerasのパワーを体感してみましょう。おそらくこれが一番簡単だと思います（もっと簡単な方法あったらすみません）。

ディープラーニングのフレームワークはGPUでの計算を手軽に使える

ディープラーニングのフレームワークを使うと、GPU（CUDA）での計算をかなり手軽に扱えるようになります。少なくともCUDAレベルからプログラミングする必要がありません。例えばC++を使ってGPUプログラミングする記事を見てみると、

CUDAを使ったGPUプログラミング超入門
https://qiita.com/Keech/items/381495ed90e012d69f1a

確かに速そうだけど、すごい闇が深そう。でも大丈夫。ここらへんは全部フレームワーク側でやってくれます。GPUによる高速化という美味しい所だけ取れます。

スパコンでも使われている連立一次方程式

以前こんなツイートがバズってました。

中学2年生「連立方程式とか社会出てから何に使うのｗ」
経済学者「めっちゃ使う」
自然科学者「連立方程式高速に解けるならすごく嬉しい」
Linpackベンチマーク「連立方程式を解く速度でスパコンを測ります」
経済学部教授金子勝「Linpackが速いだけの科学計算機能のない巨大な箱を許すな！」←New
— ロックフリーのkumagi (@kumagi) 2017年12月25日

LINPACKというスパコンのベンチマークの1つが、連立一次方程式を解いているみたいですね。

TensorFlow/Kerasを使って連立一次方程式を解き、スパコンの世界に一歩踏み入れてみましょう。

TensorFlow/Kerasでの連立一次方程式

例えば以下のような連立一次方程式をTensorFlowで解いてみましょう。

\begin{cases}
3x_1+4x_2=2 \\
4x_1+x_2=7
\end{cases}

import tensorflow as tf
import keras.backend as K
import numpy as np

def calc_equation_2():
    A = np.array([[3,4],[4,1]])
    Y = np.array([[2],[7]])
    A_tensor = K.variable(A)
    Y_tensor = K.variable(Y)
    ans_tensor = tf.matmul(tf.linalg.inv(A_tensor), Y_tensor)
    print(K.eval(ans_tensor))

if __name__ == "__main__":
    calc_equation_2()

たったこれだけです。これで2元だろうが1万元だろうがありとあらゆる連立方程式を解いてくれます。しかもGPU（CUDA）が使えれば勝手に使ってくれます。すばら！！

結果は次のようになります。

出力

[[ 2.]
 [-1.]]

$x_1=2, x_2=-1$となります。代入してみるとそのとおりですね。

2万元連立方程式を解く

正直2元連立方程式なんてGPU使うまでもありません。1万倍にして2万元連立方程式にしましょう。任意の次元の連立方程式を解けるようにしてみました。

import tensorflow as tf
import keras.backend as K
import numpy as np
import time

def calc_equation(N):
    A = np.random.rand(N, N)*2-1
    Y = np.random.rand(N, 1)*N

    start_time = time.time()
    A_tensor = K.variable(A)
    Y_tensor = K.variable(Y)
    ans_tensor = tf.matmul(tf.linalg.inv(A_tensor), Y_tensor)
    ans = K.eval(ans_tensor)
    print(time.time() - start_time)

if __name__ == "__main__":
    calc_equation(20000)

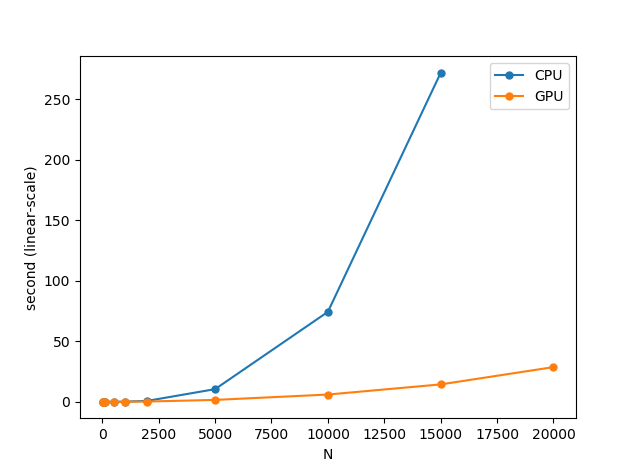
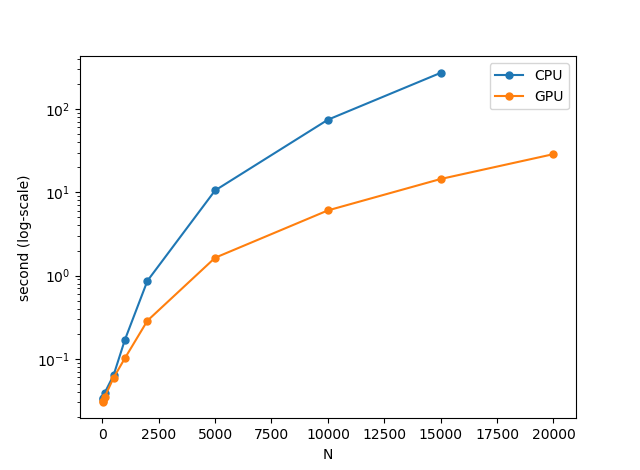
これで解けます¹。係数は適当に乱数で入れました。ついでに計算時間を測れるようにしたので、Nを変えてCPUとGPUで計算時間を測定してみましょう。単位は秒です。

N	GPU	CPU
10	0.03047	0.03296
50	0.03138	0.03346
100	0.03458	0.03884
500	0.05939	0.06379
1000	0.10173	0.16919
2000	0.28738	0.86572
5000	1.63675	10.52949
10000	6.06089	74.37334
15000	14.44360	271.74110
20000	28.71455	エラー

環境：Google ColabのCPUとGPUインスタンス
CPU: Xeon @ 2.30GHz(bogomips=4600.00)×2, メモリ12GB
GPU: Tesla K80, その他CPUやメモリはCPUインスタンスと同一
CUDA: 9.2
TensorFlow : 1.12.0-rc2, Keras : 2.1.6, Numpy : 1.14.6
Python:3.6.6
ライブラリとPythonのバージョンはCPU,GPUインスタンスともに同一

2万元の連立方程式をGPUではたった29秒で解けてしまいました！！1万元ならCPUが74秒かかるところをGPUならたった6秒で解けてしまいます。もしいいグラフィックボードを使っていたら、GPUでもっと速い結果が出ると思います。

CPUとGPUの計算性能の差が明確に出始めるのは1000元以降ですね。5000元以降はもうGPUの完勝となりました。

「連立方程式を高速に解けるならすごく嬉しい科学者」がいたらこれはぜひ教えたいですね。

ちなみに、CPUで2万元がエラーになってしまったのはメモリ不足によるクラッシュです。GPUの場合、CPUのメモリとGPUのメモリ両方使えるので多少オーバー気味にできます。

やっていることの種明かし

コードが意味わからなくてもやもやするかもしれません。やっていることは連立方程式の行列による解法です。行列を習ったことのある方は知っているかもしれません。

ここで扱っている連立方程式は、次元によらず全て以下のような行列計算で解くことができます。

\begin{align}
AX&=Y \\
X&=A^{-1}Y
\end{align}

例えば冒頭の2元連立方程式の計算

\begin{cases}
3x_1+4x_2=2 \\
4x_1+x_2=7
\end{cases}

これを行列で解くと次のようになります。

\begin{align}
\begin{pmatrix}
3&4 \\ 4 & 1
\end{pmatrix}
\begin{pmatrix}
x \\ y
\end{pmatrix} &= 
\begin{pmatrix}
2 \\ 7
\end{pmatrix} \\

\begin{pmatrix}
x \\ y
\end{pmatrix} &= 
\begin{pmatrix}
3&4 \\ 4 & 1
\end{pmatrix}^{-1}
\begin{pmatrix}
2 \\ 7
\end{pmatrix} \\

\begin{pmatrix}
x \\ y
\end{pmatrix} &= 
\begin{pmatrix}
2 \\ -1
\end{pmatrix}
\end{align}

暇な方は「逆行列　公式」とかでググって手計算で解いてみてください。これが解けなくてもTensorFlowは使えます。2万元連立方程式を手で解くのは無駄の極みなのでコンピューターに計算させましょう。手計算が終わる前におそらく寿命を迎えます。

あまりに次元を大きくすると怒られる

じゃあハードウェアが許せば5万元、10万元といけるかというと、TensorFlowの仕様によりそうはいけないようです。今後改善されるかもしれません。試しに3万元で計算したエラーがこちらです。

2GB以上の変数を割り当てられない

/usr/local/lib/python3.6/dist-packages/tensorflow/python/framework/tensor_util.py in make_tensor_proto(values, dtype, shape, verify_shape)
    504     if nparray.size * nparray.itemsize >= (1 << 31):
    505       raise ValueError(
--> 506           "Cannot create a tensor proto whose content is larger than 2GB.")
    507     tensor_proto.tensor_content = nparray.tostring()
    508     return tensor_proto

ValueError: Cannot create a tensor proto whose content is larger than 2GB.

32ビット変数で2GBというと、√(2×1024^3÷4)≒23170なので、N=2万はかなり限界すれすれだったみたいですね。

他の非機械学習の例

TensorFlowの公式チュートリアルにあります。

マンデルブロー集合の描画：https://www.tensorflow.org/tutorials/non-ml/mandelbrot
偏微分方程式：https://www.tensorflow.org/tutorials/non-ml/pdes

非機械学習のサンプルはかなりレアなので「なんかこれ面白そう」と思った例はぜひ試して記事にしてみてください。例えばポートフォリオの最適化なんか行列の最適化なんでこれでできそう²な感じはします。

まとめ

TensorFlow/Kerasは機械学習やディープラーニングの知識がなくても、単なるGPU行列計算機として利用できる。GPUパワーは強力。
CUDAの知識がなくてもTensorFlow側が勝手にやってくれるのでGPU計算としては相当ハードルが低いのではないか
TensorFlow/Kerasを使った一般的な数値計算はその有望性の割にほとんどサンプルがないので、アイディアがあったらぜひ記事にしてみてください。

連立方程式の解が不定となって解けない場合もありますが、そういう細かいことは気にしないという方針で。係数が乱数で、ある程度次元が大きければ、不定解となる確率は十分に小さいかと思われます。 ↩
Black-Littermanモデルなど　https://qiita.com/nokomitch/items/0d1812763114e6266bf3 ↩