はじめに
投資における最適ポートフォリオ選択手法であるブラック・リッターマンモデル(Black-Litterman Model)。伝統的な平均分散アプローチによる最適化と比べ直感的に理解しやすい結果が得られるため、その使い勝手の良さから金融実務でも広く用いられています。
本記事ではブラック・リッターマンモデルは何をしているのかについて、図も用いてざっくりと解説したいと思います。数式の導出など細かい部分については参考文献を確認ください。
ブラック・リッターマンモデル概観~伝統的な最適化手法との比較
伝統的な最適化手法とその問題点
マーコヴィッツによる平均分散アプローチでは、各アセットの期待リターンとリスク(共分散行列)を推定し、リターンを最大化しつつリスクを最小化するというトレードオフを最適化計算によって解くことにより、最適ポートフォリオを計算します。
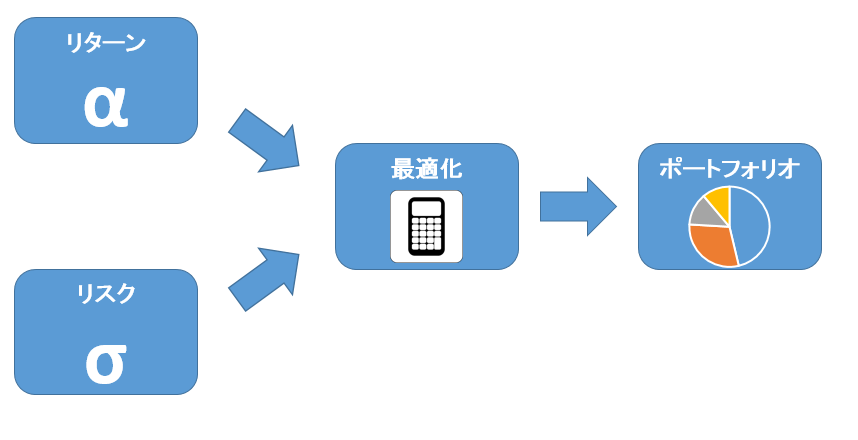
このアプローチは理解しやすいものですが、実務で利用するためには次のような問題点があります。
- リスクは比較的安定しており推定しやすい一方で、リターンの予測は難しい
- にもかかわらず、平均分散アプローチによる最適化では全てのアセットに対する期待リターンを指定しなければならない
- そのうえ、期待リターンのわずかな変化で、結果として得られるポートフォリオが大きく変わってしまう
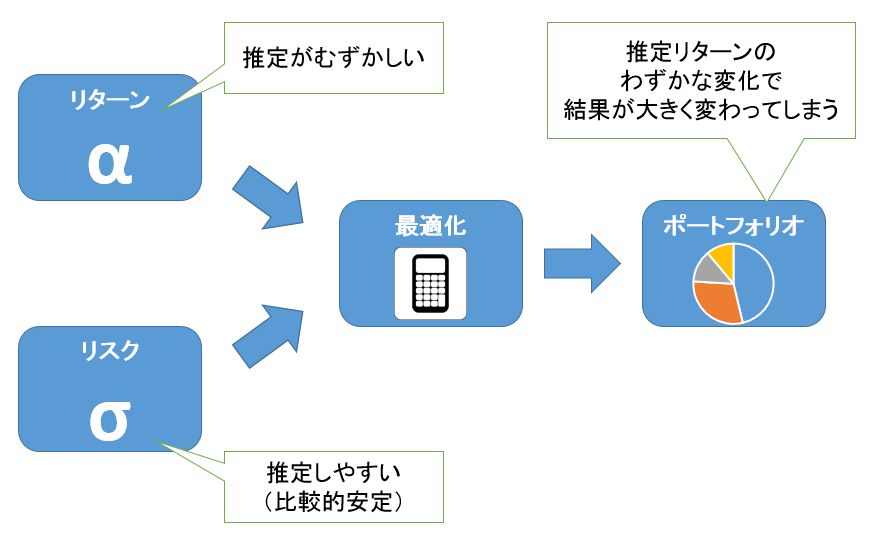
このため実務上は、最適化計算においてさまざまな制約条件(ポジションサイズ、売買回転率など)を課すことによって対応しています。
この問題点を回避するために、ブラック・リッターマンモデルが考案され、広く用いられています。
ブラック・リッターマン最適化の流れ
ブラック・リッターマンモデルは、以下3ステップに分けて考えると理解しやすいです。
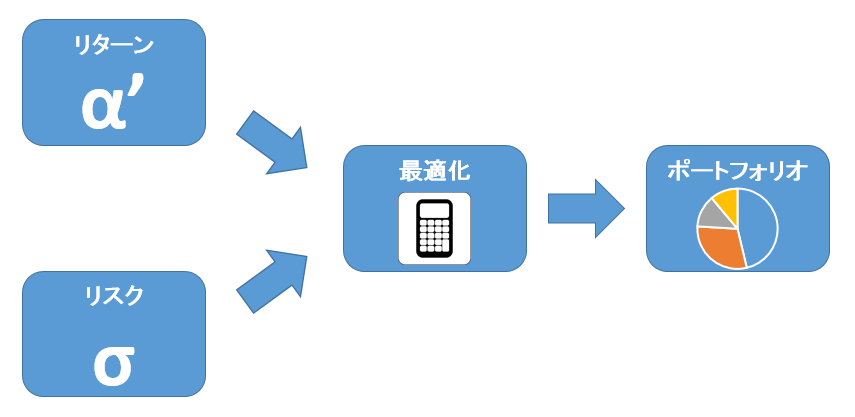
1. Reverse Optimizationにより均衡期待リターンを求める
ブラック・リッターマン最適化では、推定するのが困難な期待リターンを直接推定しません。その代わり、マーケット全体が最適化によってポートフォリオを選択している、すなわち現在の市場における時価総額ウェイト(=マーケット・ポートフォリオ)は、マーケットが想定している推定リターンとリスクを入力とする最適化の結果得られたものと仮定します。この考えに基づいて、時価総額ウェイト(マーケット・ポートフォリオ)と推定リスクから、市場が想定している期待リターン(均衡リターン、あるいはインプライドリターンと呼びます)を逆算することができます。この手法は平均分散アプローチでの最適化計算を逆に行う形になるため、Reverse Optimizationと呼ばれています。
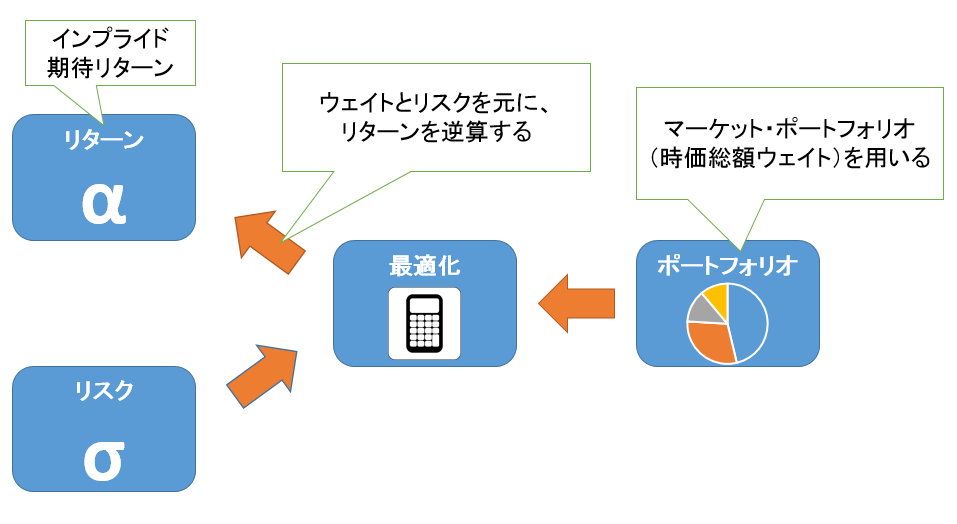
2. ベイズ更新により投資家のビューを均衡期待リターンにブレンドする
1のReverse Optimizationで求めた均衡期待リターンに、ベイズ統計を用いて投資家のビュー(見通し)をブレンドし、期待リターンの値を調整します。投資家のビューは、例えば「A資産がB資産を3%アウトパフォームする」「C資産のリターンは5%となる」などの予測の形でモデルに入力します。予測は任意の数を入力でき、各予測についての投資家の自信度もパラメータとして入力できます。自信度が高い予測はリターンに対する影響度が大きくなり、自信度が低い予測はリターンにあまり影響しないことになります。
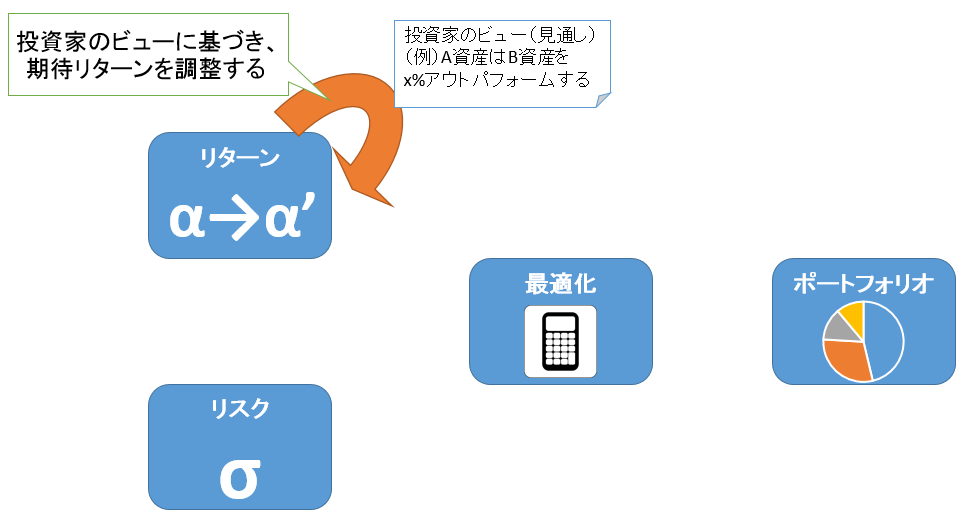
3. 最適化計算によりポートフォリオを計算
最後に、更新された期待リターンとリスクをもとに、最適化プロセスによって新ポートフォリオを計算します。
数式 & Pythonによる実行例
それではブラック・リッターマンモデルに登場する数式、ならびにPythonで実装したコードも紹介します。
ここでは、He & Litterman(1999)論文 の数値例を再現します。
0.準備
He&Litterman論文では、7カ国(オーストラリア、カナダ、フランス、ドイツ、日本、UK、米国)の株式インデックスのポートフォリオを例としています。その時価総額ウェイト$w$、相関行列、ボラティリティがインプットとして与えられています。
これらのデータをPythonで準備しておきます。
共分散行列 $\Sigma$ (Sigma) は相関行列(correlation)とボラティリティ(std)から計算します。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# ウェイト
w = np.array([[0.016, 0.022, 0.052, 0.055, 0.116, 0.124, 0.615]]).T
# 相関行列
correlation = np.array([
[1, 0.488, 0.478, 0.515, 0.439, 0.512, 0.491],
[0.488, 1, 0.664, 0.655, 0.310, 0.608, 0.779],
[0.478, 0.664, 1, 0.861, 0.355, 0.783, 0.668],
[0.515, 0.655, 0.861, 1, 0.354, 0.777, 0.653],
[0.439, 0.310, 0.355, 0.354, 1, 0.405, 0.306],
[0.512, 0.608, 0.783, 0.777, 0.405, 1, 0.652],
[0.491, 0.779, 0.668, 0.653, 0.306, 0.652, 1]])
# 標準偏差
std = np.array([[0.16, 0.203, 0.248, 0.271, 0.21, 0.2, 0.187]])
# 相関行列と標準偏差から共分散行列を計算
Sigma = correlation * np.dot(std.T, std)
# パラメータdelta 値はHe&Litterman(1999)に従う
delta = 2.5
# パラメータtau 値はHe&Litterman(1999)に従う
tau = 0.05
また、以降の数式で登場する記号は以下のとおりです。
$\Pi$ 均衡期待リターン(nx1ベクトル)
$\Pi'$ 投資家のビューを考慮して更新された期待リターン(nx1ベクトル)
$w$ 当初ウェイト (nx1ベクトル)
$w'$ 事後ウェイト (nx1ベクトル)
$\Sigma$ リターンの共分散行列
$P$, $Q$ 投資家のビューを示す行列
$\Omega$ 投資家のビューに対する確信度を示す行列
$\delta$ パラメータ(投資家のリスク回避度を表す)
$\tau$ パラメータ(共分散行列に対する信頼区間を表す)
1. Reverse Optimization
第一ステップはreverse optimization。、つまり最適化を逆に行う計算です。上で説明したように、通常の最適化では「リターン」と「リスク」を入力として、リターンを最大化・リスクを最小化するトレードオフを最適化計算し「ポートフォリオ(ウェイト)」を求めます。reverse optimizationではこれと反対に「ポートフォリオ(ウェイト)」と「リスク」を入力として、「リターン」を求めます。
最適化計算における効用関数は以下の式で表され、この$U$を最大化する$w$が最適ポートフォリオとなります。式中の $\delta$ はリスク回避度を指定するパラメータです。
U = w^T\Pi - \frac{\delta}{2} w^T \Sigma w
この$U$を$w$で微分し、それが0となる$w$が最適ポートフォリオとなります。
\frac{dU}{dw} = \Pi - \delta\Sigma w = 0
これを$\Pi$について解くと
\Pi = \delta\Sigma w
この式を用いて均衡期待リターン$\Pi$を求めることができます。
Pythonでは次のように実行します。
# 均衡リターンを求める(reverse optimization)
r_eq = delta * np.dot(Sigma, w)
2. 均衡リターンに投資家のViewをブレンドする
次に、投資家のView(見通し or 予測)を指定し、これを先に求めた均衡リターンとブレンドして、新たな期待リターンを求めます。
ブラック・リッターマンモデルにおいて、投資家のViewは 2つの行列 $P$と$Q$で表現します。
He&Litterman論文の例では、
P = \left( \begin{array}{cccccc} 0 & 0 & -0.295 & 1 & 0 & -0.705 & 0 \\\
0 & 1 & 0 & 0 & 0 & 0 & -1 \end{array} \right) \\\
Q = \left( \begin{array}{c} 0.05 \\\ 0.03 \end{array} \right)
のようになっています。これは「ドイツがその他欧州(フランス、UK)を5%アウトパフォームする」「カナダが米国を3%アウトパフォームする」という2つのViewを表しています。
また、この2つのViewに対する確信度を$\Omega$という行列で指定します。論文の例では以下のような値になっています。
\Omega = \left( \begin{array}{cc} 0.001065 & 0 \\\ 0 & 0.000852 \end{array} \right)
これらの行列もPythonで準備しておきます。
P = np.array([
[0,0,-0.295,1,0,-0.705,0],
[0,1,0,0,0,0,-1]]) # 2x7 matrix (2: number of views, 7: number of assets)
Q = np.array([[0.05],[0.03]]) # 2-vector
Omega = np.array([
[0.001065383332,0],
[0,0.0008517381]])
いよいよ、Black-Littermanの"master equation"を用いて、均衡リターンに投資家のViewをブレンドし、新たなリターンを求めます。その式は以下のとおりです(導出は参考文献の論文に詳しく解説されています)。
\Pi' = \Pi + \tau \Sigma P^T \left( P \tau \Sigma P^T + \Omega \right)^{-1} \left( Q - P\Pi\right)
行列の掛け算と逆行列が入った式ですが、Pythonで書くとこうなります。
# 均衡リターンに投資家のビューをブレンドする
r_posterior = r_eq + np.dot( np.dot( tau*np.dot(Sigma,P.T), np.linalg.inv(tau*np.dot(np.dot(P,Sigma),P.T)+Omega)), (Q-np.dot(P,r_eq)))
リターン$\Pi$と同時に、共分散行列$\Sigma$も次のように更新します。
\Sigma' = \Sigma + \tau\Sigma - \tau\Sigma P^T \left( P \tau \Sigma P^T + \Omega \right)^{-1} P\tau\Sigma
Pythonで書くと以下のようになります。
Sigma_posterior = Sigma + tau*Sigma - tau*np.dot( np.dot( np.dot(Sigma,P.T), np.linalg.inv(tau*np.dot(np.dot(P,Sigma),P.T)+Omega)), tau*np.dot(P,Sigma))
3. 最適化により新しいウェイトを求める
最後に、更新されたリターン $\Pi'$ と共分散行列 $\Sigma'$ をもとに最適化計算をして、新しい最適ウェイト$w'$を求めます。
ここでは、新しいウェイト $w'$ は最適化問題を解析的に解いた以下の式で求めます。
w' = \Pi' (\delta\Sigma')^{-1}
コードで書くと
# Forward Optimizationをして最適ウェイトを求める
w_posterior = np.dot(np.linalg.inv(delta*Sigma_posterior), r_posterior)
となります。
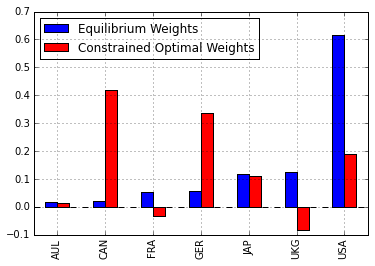
旧ウェイト $w$ と 新ウェイト $w'$ をグラフにプロットしてみましょう。pandasのプロット機能を使っています。
df = pd.DataFrame([w.reshape(7),w_posterior.reshape(7)],
columns=['AUL','CAN','FRA','GER','JAP','UKG','USA'],
index=['Equilibrium Weights','Constrained Optimal Weights'])
df.T.plot(kind='bar', color='br')
結果はこのようになりました。青がもともとの時価総額ウェイト、赤が新しく計算された、投資家のビューを組み入れたポートフォリオウェイトを表しています。投資家の見通しに基づいてカナダ・ドイツのウェイトが増加し、フランス・英国・米国のウェイトが減少する、という結果になりました。
おわりに
モデルの実装においては$\delta, \tau, \Omega$などのパラメータ設定が肝となり、設定手法もいろいろと議論されてそれだけで論文になっていたりしますが、今回は省きました。
何となく難しそうな響きのあるブラック・リッターマンモデルですが、意外と簡単だったのではないでしょうか?記事でも説明したように、従来の平均-分散最適化手法のように突拍子もない結果が出てくることが少なく、使い勝手がよい手法です。資産数が少なければExcelでも十分計算可能なものです。
日本語の文献も限られているので、ご理解の一助になるようでしたら幸いです。
参考文献
- blacklitterman.org - Jay Walters氏のサイト
- The Black-Litterman Model In Detail - Jay Walters氏のペーパー。オリジナルのBLモデルに加えて、さまざまな派生系も網羅しています