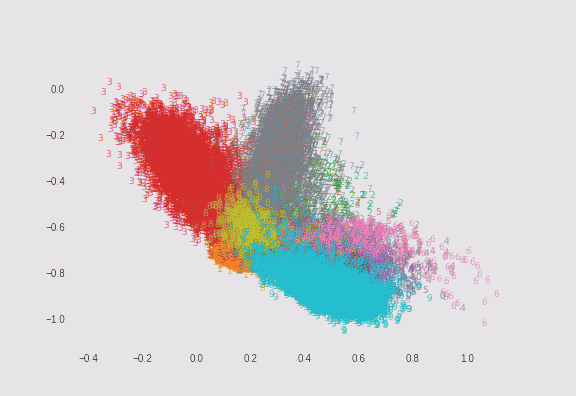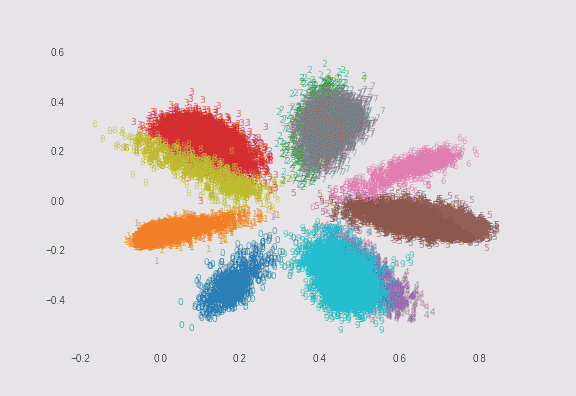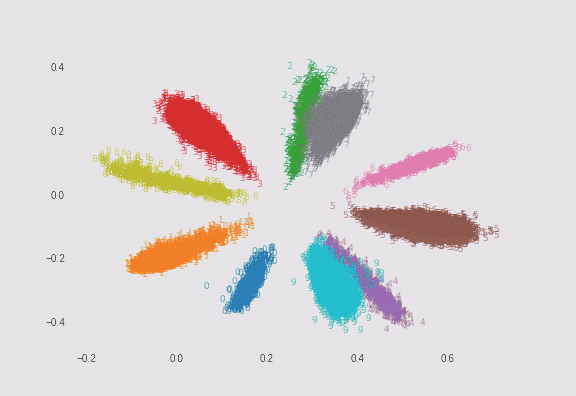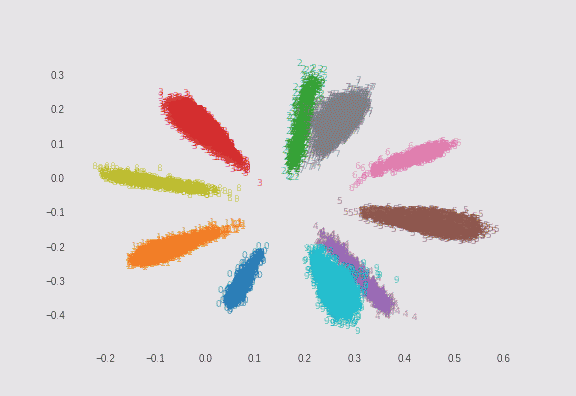不均衡データへの対策は、現実問題での精度を上げるうえで大事な問題です。つい先々週に(2019/1/23)出た論文ですが、不均衡データ対策に重点を置いた損失関数「Affinity Loss」というのが発表されていたので、それを読んで実装しておきたいと思います。
ざっくりいうと
- ソフトマックスにクラスタリングの要素を持ち込んで、不均衡を是正するアルゴリズム。サポートベクターマシンのようなマージン最大化問題を考える。
- さらにプロットに「diversity regularizer」という正則化をいれ、プロットにおけるサンプル数の不均衡を補正する
- 論文通りにMNISTでの有効性は再現できたが、一般的な画像データセットに対して不均衡補正が有効に機能するかは議論の余地がある
元の論文:Munawar Hayat, Salman Khan, Waqas Zamir, Jianbing Shen, Ling Shao. Max-margin Class Imbalanced Learning with Gaussian Affinity. 2019. https://arxiv.org/abs/1901.07711
自分の実装:https://github.com/koshian2/affinity-loss
若干前置きが長いので内容だけ見たい方は「Affinity lossの理論」まで飛ばしてください。
追記(2/14):CIFAR-10についていろいろ試してみました。一応結果が出るようになりました。簡単にいうと、**Data Augmentationするとよくなる、評価尺度がMacro F1よりもMicro F1のほうがわかりやすいのでは?**ということでした
Affinity LossをCIFAR-10で精度を求めてひたすら頑張った話
https://blog.shikoan.com/affinity-loss-cifar/
不均衡データとは
クラス間のデータ数に偏りがあるケース。例えば珍しい病気があったとして、それの検出をしたいとしましょう。
| クラス | データ数 |
|---|---|
| 陽性 | 100 |
| 陰性 | 9900 |
陰性のデータは1万件近く集めることができましたが、陽性のデータは100件しか集められませんでした。このように、陽性・陰性というクラス間でデータ数に明らかな偏りがあるケースを**不均衡データ(inbalanced data)**といいます。
不均衡データの問題点
評価上の問題
これは教科書的な問題で、「精度(Accuracy)が機能しない」という点です。例えば先程の例で陰性がデータ全体の99%なら、ありとあらゆるデータに対して陰性と判定($y=0$)する分類器を作れば、その時点で精度99%を達成してしまいます。
def classifier(input):
return 0
こんなイメージです。機械学習なんていらないですね。笑っちゃうかもしれませんが、実は機械学習を使っても「return 0」みたいな状態に最適化が向かうことがあります(後述)。
今最適化での解の問題はおいておくとして、あくまで評価上の問題なら、Precision, Recall, ROC曲線、F1スコアなどの指標を使えば不均衡データに対応できます。Precision、Recallの調和平均であるF1スコアを精度の代替として使うのが一番わかりやすいですね。
最適化の問題
実はこちらのほうが深刻です。今2値分類を考え、推定値を$\hat{y}_i$、真の値を$y_i$としたときに、**交差エントロピー(binary crossentropy)**による損失関数は、
$$-\sum_i^N(y_i\log\hat y_i + (1-y_i)\log(1-\hat y_i)) \tag{1}$$
となります。これは陽性と陰性のデータが半々あるような、均衡データの場合はとてもよく機能します。しかし、不均衡データの場合はどうでしょう?
もし、陰性のデータが陽性のデータより100倍近くもあれば、陰性が出やすいように(多クラス分類ならデータ数が大きいクラスが出やすいように)最適化されやすいということを意味します。なぜなら、(1)の式の構成要素の大半は陰性のデータで、陰性の交差エントロピーを合わせてしまえば全体の損失が下がってしまうからです。
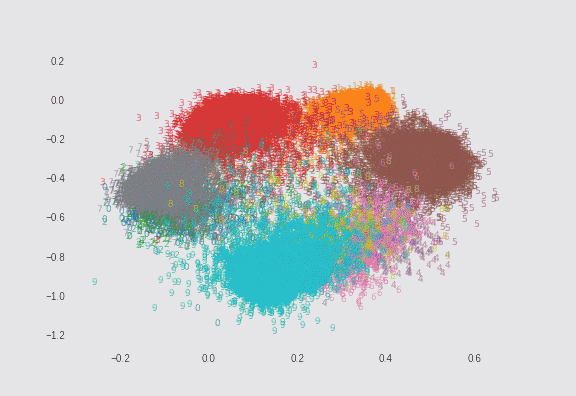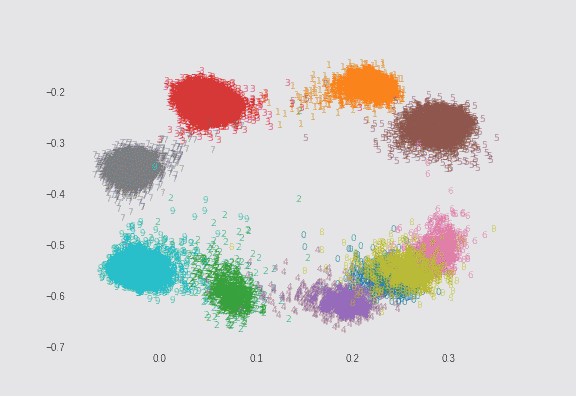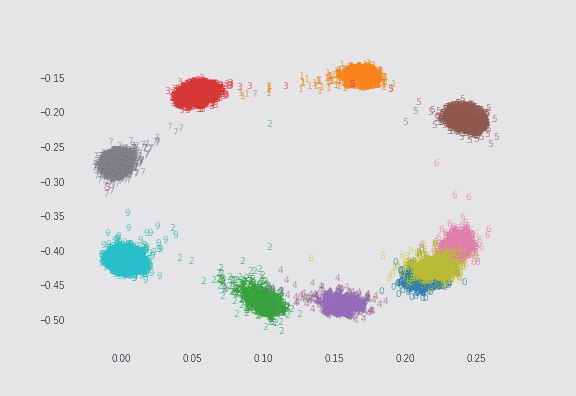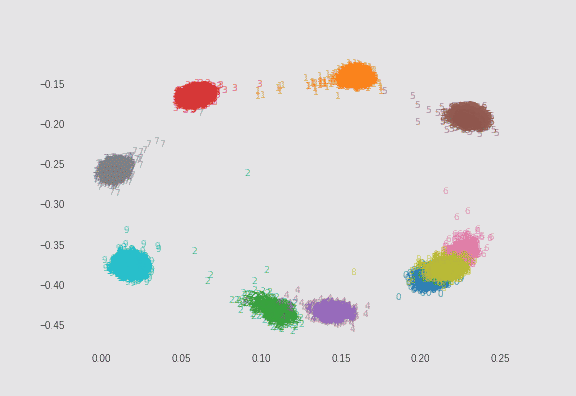
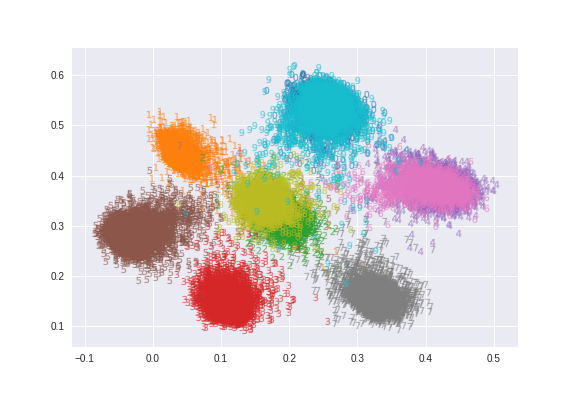
「return 0」みたいな極端な状態にはならなくても、実際問題陽性側のニューロンは訓練されにくいです。直感的な例として、このAffinity Lossの論文(M.Hayat et al.(2019))に載っていた図を示します。これは多クラス分類のソフトマックスの損失関数ですが、今述べたようなシチュエーションがおこります。
MNISTの手書き数字6万サンプルのうち、0~4は全体の10%、5~9はそのまま使って不均衡データを再現しています。ソフトマックスが計算に使っている特徴量を2次元に投射したものですね。このように、データ数が少ない不均衡なクラスは、それだけプロット領域が小さくなり(オレンジ色=1など)、ソフトマックスがうまく検出できなくなる。つまり、データ数の不均衡度がそのまま潜在的な特徴量にも継承され、それが分類のパフォーマンスを悪化させるという現象が起こります。
不均衡データへの対策
データレベルの対策
最も有効性が確かめられているのは少ないクラスのOversampling/多いクラスのUndersamplingでしょう。自分はOversamplingのほうが好きです。(1)の式は陽性と陰性のデータ数が全然違うのが問題であって、Data Augmentationなどを噛ませながら(別になくても機能するそうです)、不均衡を補正するようにサンプリングすれば多少マシになるという仕組みです。例えば、「ランダムサンプリングするが、陽性のデータに10倍、20倍を確率の重みをつけてサンプリング」するということです(Oversampling)。
ただし、この論文によると、Oversamplingはオーバーフィッティングや冗長性の影響を受けやすし、Undersamplingは致命的な情報損失を受けやすいとのことです。ただし、自分の経験から言えばOversamplingでData Augmentationすればそこまで悪くはないです。昔からあるのサンプリングアルゴリズムの「SMOTE(Synthetic Minority Over-sampling Technique)」も今で言えばData AugmentationしながらOversamplingしていると考えることができます。
アルゴリズムレベルの対策
**コスト考慮型学習(cost-sensitive learning)**というそうです。自分はこの言葉初めて聞いたのですが、多分陰性と陽性に異なるペナルティ係数をつけて学習させるようなことだと思います。
この論文には出ていなかったのですが、この論文へのアプローチに似た、不均衡データの対策した損失関数というのはすでにあってT.Y.Lin et al.(2017)のFocal lossが有名。ただしFocal lossは物体検出用なので、分類問題で効くかどうかの議論はありません。ただし、この論文である「Affinity loss」のほうがプロットの分散調整をしているので、直感的にはAffinity lossのほうが効くような気はします。
従来のアプローチでどれぐらいのデータ数が必要か
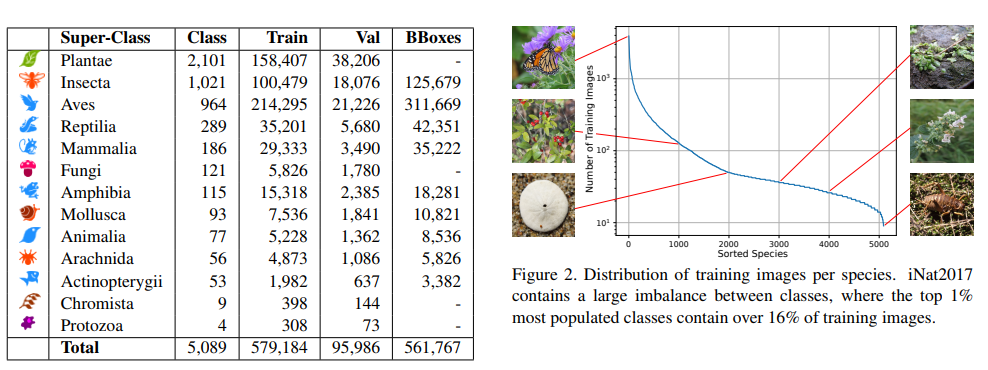
不均衡データをソフトマックス関数で分類する場合、クラスあたりの枚数と精度の関係は気になります。この論文からは外れるのですが、「The iNaturalist Species Classification and Detection Dataset」(G.V.Horn(2017))という論文によれば、
このような動植物の画像(5089クラス67.5万)という画像データを分類(物体検出)しています。大きなカテゴリーとして植物(Plantae)、昆虫(Insecta)、鳥類(Aves)などがありますね。ただし、かなり不均衡データで、右の図のように「1クラス1000枚以上もあるクラスもあれば、1クラス10枚程度しかない場合もある」というような状況です。アゲハチョウのように簡単に見つけられる種もあれば、とてもレアな種もありますからね。
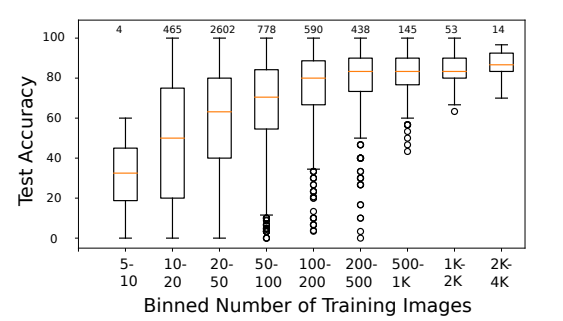
これをInceptionResNet V2 SEで訓練したところ、クラスあたりのサンプル数とテスト精度の関係は以下のようになったとのことでした。
最低でも1クラスあたり50枚はないと精度がガクッと落ちるのがわかります。反対に1クラス500枚の画像を2000枚にしてもそれほど効いていないのがわかります。
これはつまり、ソフトマックスのプロットが、先程見たように画像が少ないクラスは大きいクラスに押されて小さくなっているため、他のクラスと混ざりやすくなったり、オーバーフィッティングしやすくなっているからというのが背景にあります。
ソフトマックスの問題点
メインの論文に戻ります。Affinity lossの論文では、ソフトマックスの問題点として3点挙げられていました。
- マージン最大化のアプローチを組み込めない
- 分類空間上での射影ベクトルがクラス間で等間隔にプロットされることが保証されない
- 射影ベクトルの長さ$||w_j||_2$がクラス間で同一になることが保証されない
1点目はサポートベクターマシン(SVM)のようなマージンの概念を組み込みたいのです。クラス間にマージンがあったほうが綺麗に分類できるからです。2点目は難しい言葉を使っていますが、要は下の図で、大きなクラスだろうが小さなクラスだろうが同一のサイズで、かつ同じようにプロットしてほしいということです。
このソフトマックスの問題点を解決したのが、Affinity lossでこれを使うとこのようなプロットになります。
実際に試したら自分の実装が悪かったのかここまで綺麗なプロットにはならなかったのですが、直感的にはこんなイメージです。
Affinity Lossの理論
ここからが論文のメインです。行列の次元数は論文の表記ではなく、自分が多分こんなのだろうと思ったものなので、間違いがあったら指摘してください。
ユークリッド空間での類似度
入力$\boldsymbol{f}$を$(N,h)$次元、重み$\boldsymbol{w}$を$(C,h)$次元とします。$N$はミニバッチ数、$h$は入力の隠れ層の数(2次元にプロットするなら2)、$C$はクラス数です。もしソフトマックスによる損失関数なら(これは使いません)
L_{sm} = \frac{1}{N}\sum_i -\log\biggl(\frac{\exp(\boldsymbol{w}_{y_i}^T\boldsymbol{f}_i )}{\sum_j\exp(\boldsymbol{w}_j^T\boldsymbol{f}_i )}\biggr) \tag{2}
となります。ここで$y_i$は$i$番目のサンプルに対応するラベル(onehotベクトルの値)となります。まず、類似度の指標$d(f_i, w_j)$を定義します。
d(\boldsymbol{f}_i, \boldsymbol{w}_j) = \exp\bigl(-\frac{\|\boldsymbol{f}_i-\boldsymbol{w}_j\|^2}{\sigma} \bigr) \tag{3}
ここで$\sigma$はハイパーパラメータです。$d(f_i, w_j)$はベクトル同士の類似度なので、類似度の行列は$(N,C)$次元になります。これにより、以下の5点を保証することができます。
- マージン最大化を適用できる
- 複数のクラスに対して等間隔の決定境界がある
- クラスタリングの分散を制御し、クラス内のコンパクト性を上げる
- 類似度を計測するために標準的なユークリッド距離を使えること
- クラスタリングと分類を同時並行的に行えること(これが一番重要らしい)
つまり、ソフトマックスの問題を解消するために、分類問題にクラスタリングの要素を入れたということです。論文中に確率という言葉は使われていませんでしたが、(3)はほとんど正規分布($\pi$でスケーリングしていないだけ)なので、直感的にはユークリッド距離を正規分布(正確に言うならガウスカーネル)に変換して類似度を測っているだけとも言うことができます。このへんはt-SNEの発想っぽいですよね。
損失関数その1:クラス間のマージンと損失関数
Affinity lossは2つの項からなります。**1つ目はマージン最大化のためのクラス間のマージン項$L_{mm}$**です。
L_{mm} = \sum_j \max\bigl(0, \lambda+d(\boldsymbol{f}_i, \boldsymbol{w}_j)-d(\boldsymbol{f}_i, \boldsymbol{w}_{y_i})\bigr):j\neq y_j \tag{4}
$\lambda$はクラス間のマージンを表すハイパーパラメータです。
これはFaceNetのTriplet-lossとかなり似ています。$d(f_i, w_j)$は異なるクラス間の類似度、2つ目の$d(f_i, w_{y_i})$は同じクラスの類似度です。それぞれTriplet lossのNegative、Positiveに対応します。ただし、Triplet lossは距離を入れるのに対し、Affinity lossは類似度を入れるので大小関係が変わります。距離の場合は近いほうが値が小さくなるのに対し、類似度は近いほうが値が大きくなるからです。
ちなみに、$d(f_i, w_j)$は$(N,C)$の行列になるのに対して、$d(f_i, w_{y_i})$は$(N,1)$の行列になるので、和でreduceさせ、$L_{mm}$は$(N,)$のベクトルとなります。
クラス間のマージンの理解
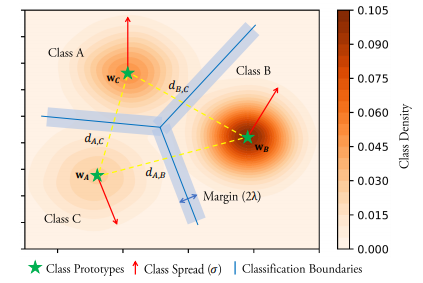
マージンの直感的な理解は論文の図がわかりやすいです。
ちょうどSVMのマージンそのものですね。SVMのマージン最大化をニューラルネットワーク上でやろうとしていると考えて良いでしょう。
もう少しマージンの意味について突っ込んで考えてみます。この類似度はスケーリングしない正規分布と考えるのがわかりやすいと思います。もし(3)式の分子が0、つまり、$\boldsymbol{f}$と$\boldsymbol{w}$の差が0なら、類似度は1になり最大値になります。今$\sigma=1$とし、標準正規分布の確率密度関数を$p(x)$とすると、
d(\boldsymbol{f}_i, \boldsymbol{w}_j) = \exp\bigl(-\|\boldsymbol{f}_i-\boldsymbol{w}_j\|^2 \bigr) = \frac{p(\|\boldsymbol{f}_i-\boldsymbol{w}_j\|^2)}{p(0)} \tag{5}
となりますからね。とりあえず**$d$のとる値は0~1**であるというのを覚えておきましょう。次に$L_{mm}$の式の中身を分解して考えます。
1つ目の$d$をN(Negative)、2つ目の$d$をP(Positive)として$\lambda$の値別にプロットしてみます。表の左上のほうがそのクラスに近い(類似度が高い)を意味します。
- $\lambda=0.01$の場合
| N/P | 1 | 0.75 | 0.5 | 0.25 | 0 |
|---|---|---|---|---|---|
| 1 | 0.01 | 0.26 | 0.51 | 0.76 | 1.01 |
| 0.75 | 0.00 | 0.01 | 0.26 | 0.51 | 0.76 |
| 0.5 | 0.00 | 0.00 | 0.01 | 0.26 | 0.51 |
| 0.25 | 0.00 | 0.00 | 0.00 | 0.01 | 0.26 |
| 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 |
- $\lambda=0.75$の場合
| N/P | 1 | 0.75 | 0.5 | 0.25 | 0 |
|---|---|---|---|---|---|
| 1 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 |
| 0.75 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 |
| 0.5 | 0.25 | 0.50 | 0.75 | 1.00 | 1.25 |
| 0.25 | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 |
| 0 | 0.00 | 0.00 | 0.25 | 0.50 | 0.75 |
$\lambda$が小さい場合は、正解(Positive)の確率の高いゾーンに入ってしまったらそれ以上はほとんど学習しません。もしすぐ近くに不正解(Negative)のゾーンがあって重なっていてもほとんど気にしません。
逆に$\lambda$が大きい場合は、正解の(Positive)確率が高いゾーンに入っていても、すぐ近くに不正解のゾーンがあり、不正解の確率が高ければかなり気にします。例えばN/Pが互いに1のケースで、$\lambda=0.75$の場合は、0.75もロスがありますからね。このロスは互いのクラスを引き離す方向で学習を進め、結果的に$\lambda$がクラス間の物理的なマージンとして可視化されるというわけです。
またこのマージンは、損失関数の2つ目の項と合わせることで、クラスのプロットをよりコンパクトにする機能があります。$\lambda$が高いほうがよりプロットをコンパクトにさせようとする力が強く働きます。不正解のゾーンが近くになくても(N=0でも)、正解の中心からやや遠ければ(例P=0.5)、まだ正解の中心に向かおうとするからです。つまり、$\lambda$が高いケースではより多くの点に対して求心力が働きます。
これは裏を返せば、$\lambda$が小さいケースでは、中心からある一定以内の類似度の点を、それ以上中心に向かわせようとはしないよということにもなります。小さくなりすぎて困るケースでは、$\lambda$を下げればよいと思います。
$\lambda=0.01$の場合と、$\lambda=0.75$の場合でMNISTを2次元にプロットしてみました。どちらも$\sigma=5$としています。ただし偶数の数字のみサンプル数を1/10にして不均衡データにしています(これは自分が実装しました)。
λによる求心力が非常に強いので、円形に近いプロットになります。ただし、より多くの点を中心に向かおうとさせようとしているので、離れた場所にある点の移動が疎かになっているようにも見えます。
よく見ると、偶数のサンプル数が1/10であるにもかかわらず、プロットサイズがあまり変わらないようになっています。これは損失関数の2つ目の正則化項が機能しているからです。
損失関数その2:分類領域の均一化
$L_{mm}$だけではプロットのサイズが不均衡度で変化してしまうので、このサイズをデータの不均衡度に依存しないように保証させます。これを論文ではdiversity regularizerと読んでおり、正則化項として機能します。diversity regularizerは$R(\boldsymbol{w})$で表します。
\begin{align}
R(\boldsymbol{w})&=\mathbb{E}\bigl[(\|\boldsymbol{w}_j-\boldsymbol{w}_k\|^2-\mu)^2\bigr], s.t. j<k \\
\mu &= \frac{2}{C^2-C}\sum_{j<k}\|\boldsymbol{w}_j-\boldsymbol{w}_k\|^2 \tag{6}
\end{align}
$\boldsymbol{w}$は$(C,h)$次元なので、$\boldsymbol{w}$どうしのノルムを取ると$(C,C)$次元になります。$j<k$の部分はこれの上三角行列を取って、対角成分を抜けばOKでしょう。この母数が$\frac{C^2-C}{2}$になるので、$\mu$はばらつきの平均ということになりますね。
あとは$\mu$を使って偏差平方和を取れば良いので、同じようにして計算すると$R(\boldsymbol{w})$が出ます。$\mu$が平均なら、$R(\boldsymbol{w})$はこれの分散といえるでしょう。この分散がdiversity regularizerであり、これを正則化項として損失関数に足します。具体的には、
$$L = L_{mm} + R(\boldsymbol{w}) \tag{7}$$
これでAffinity lossの基本的な損失関数が完成しました。ちょっと難しかったかもしれません。
発展形:複数のクラスタの中心を持つ学習
実はこれの発展形で、1クラスに対して複数の中心(クラスタ)をもたせることができます。MNISTを2次元にプロットするケースだとまずいらないと思いますが、次元数が大きくなったりデータの潜在特徴量がバラバラだと複数のクラスタをもたせることは意味があります(正規分布の合成のような表現になります)。
次のように変えます。まず、$\boldsymbol{w}:(C,h)\to(C,m,h)$に変更。$m$は1クラスあたりのクラスタ数です。行列からテンソルになりますが、特に積の計算はしないのでただの配列変数です。
次に(3)式の類似度の定義を複数のクラスタに対応させ、
d(\boldsymbol{f}_i, \boldsymbol{w}_j) = \max\biggl\{\exp\bigl(-\frac{\|\boldsymbol{f}_i-\boldsymbol{w}_{j,t}\|^2}{\sigma} \bigr)\biggr\}, t=[1,m]\tag{8}
ちょっとここらへんの計算が論文ですっ飛ばされていて間違っているかもしれませんが、多分次のような計算をするのではないかと思います。
- 元の次元が$(N,h)$である$\boldsymbol{f}$を$(N,1,1,h)$とランクを増やす。4階テンソルになる。
- 元の次元が$(C,m,h)$である$\boldsymbol{w}$を$(1,C,m,h)$とする
- expの中のノルムを計算することで$h$の軸がreduceされ、ノルムは$(N,C,m)$となる
- max関数で$m$の軸がreduceされ、今までの場合と同様に、類似度の行列は$(N,C)$の次元になる
またdiversity regularizerは、単に$\boldsymbol{w}$が$(mC,h)$次元の行列として考えます。事前にreshapeすれば良いですね。ただし、母数の係数は、
$$\frac{2}{(mC)^2-mC} $$
となります。最終的な損失は同様に$L = L_{mm} + R(\boldsymbol{w})$で計算することには変わりありません。
論文での精度
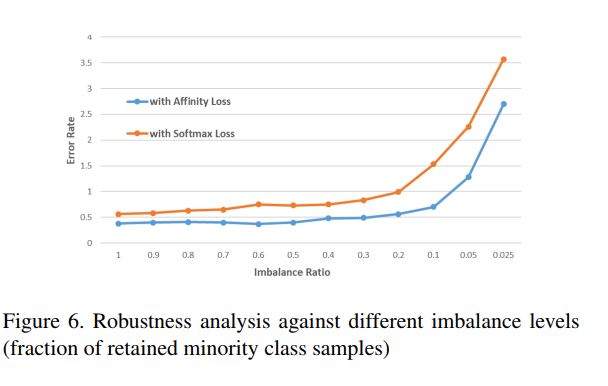
論文で述べられていた精度です。横軸に不均衡度を取り、ソフトマックスとAffinity lossの精度を比較したものです。MNISTの結果です。
ソフトマックスに対して常に良い結果を出したとのことです(これどうやってチューニングしたんだという疑問がががが)
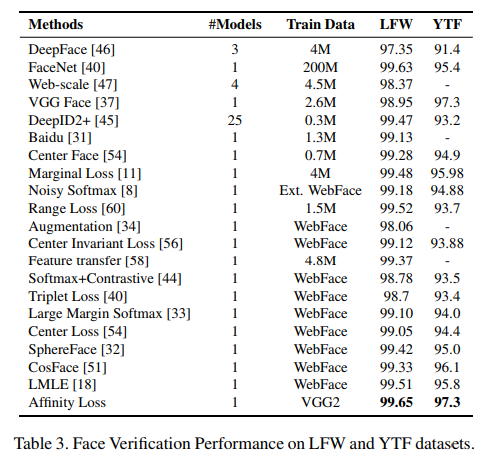
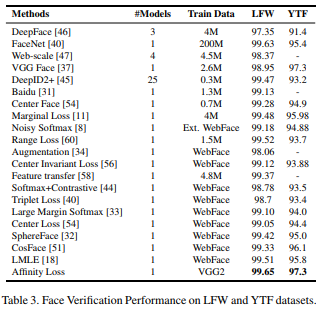
また、顔認証のデータに対して優秀な成績を残したとのことです。
再現実験
MNISTとCIFAR-10で論文での結果を再現してみました。
MNIST
このような構成のCNNです。ConvはすべてConv→BN→ReLUになります。
| レイヤー | チャンネル数 | カーネル/Stride | 繰り返し |
|---|---|---|---|
| Conv | 32 | 3 | 1 |
| AvgPool | - | 2 | 1 |
| Conv | 64 | 3 | 1 |
| AvgPool | - | 2 | 1 |
| Conv | 128 | 3 | 1 |
| Global AvgPool | - | - | 1 |
| Batch Norm | - | - | 1 |
| Affinity loss | 10 | - | 1 |
基本的には2つの軸で動かします。
- データの不均衡の度合いの軸。偶数の数字のサンプル数を変えて不均衡度を変化させます
- アルゴリズムの軸。Softmax, Affinity loss(m=1)、Affinity loss(m=5)の3ケースで比較
もうちょっと正確に条件を書くとこんな感じ。
- Affinity Lossは$m=1,5$を試した。$\sigma=10$, $\lambda=0.75$とする。
- Adamオプティマイザーを使い、初期学習率は1e-3。100エポック訓練させ、50エポックと80エポックで学習率をそれぞれ5で割った。
- バッチサイズは128
- Weight DecayやData Augmentationはなし
- MNISTのテストデータを基準に、オリジナルは1クラスあたり1000個あるものと考える。偶数の数字のテストデータの1クラスあたりのサンプル数を500、200、100、50、20、10と変化させる。奇数の数字はそのまま使う。訓練データのサンプル数は、テストデータの6倍で考える。例えば、テストデータの偶数を200枚/クラスのケースでは、訓練データの偶数は1200枚/クラス、訓練データの奇数は変わらずに6000枚/クラス、テストデータの奇数は1000枚/クラスとなる。
- TensorFlow/KerasのGPUで訓練する
- すべてのケースについて5回試行した
- テストデータの精度とF1スコア(macro)を計測したが、不均衡データなのでF1スコアで比較するのがおそらく適切
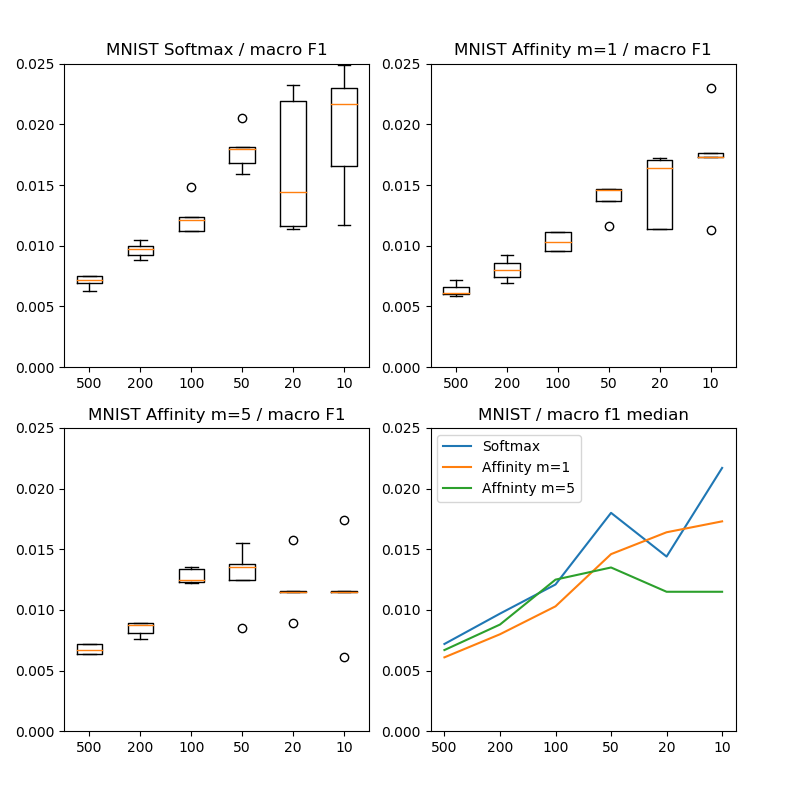
結果は以下の通り。
こちらはマクロF1スコアで比較していますが、ほぼ論文通りの結果が再現できました。Affinity lossを使ったほうが良くなっています。横軸の数字はテストデータにおける不均衡クラスのサンプル数です。100というのは多いクラスと比較して10倍の不均衡があることを示します。
MNISTの結果では、特に10や20(100倍や50倍)のような強い不均衡下でAffinity lossがパフォーマンスの劣化を抑えることが確認できました。
CIFAR-10
論文ではCIFARは確認されていませんでしたが、やはり本格的に扱うのならCIFARぐらいは確認しておいたほうが良いかと思います。ただしCIFAR-10の高次元はかなり複雑(t-SNEでプロットしてみるのがわかりやすいです)なのでMNISTみたいにアバウトな設定では精度が出ません。試しにMNISTと同じ設定でやると、明らかにソフトマックスよりも悪くなります(数%~10%とかそういうレベルで)。ハイパーパラメータのチューニングが必要です。
そこで、ちょっと本気を出してOptunaを使いハイパーパラメータを探してみました。クラスあたりのサンプル数が200のケースで、TPUを2つ使い半日ほど探させてみた(200試行×2)のですが、以下の2パターンが特によかったです。
lambda:0.4665, sigma:77.63 n_centers:9 / f1 = 0.813
[I 2019-02-04 07:22:32,144] Finished a trial resulted in value: 0.18699593819303995. Current best value is 0.18699593819303995 with parameters: {'lambda': 0.4665084469311193, 'sigma': 77.6332579550003, 'n_centers': 9}.
lambda:0.4353, sigma:90.69 n_centers:10 / f1 = 0.8216
[I 2019-02-04 08:29:54,442] Finished a trial resulted in value: 0.17838215898090493. Current best value is 0.17838215898090493 with parameters: {'lambda': 0.43527814607240023, 'sigma': 90.68981376422424, 'n_centers': 10}.
200試行ではとても足りないのでこれがベストとは言えませんが、CIFAR-10の場合、どうも$\sigma$をかなり大きめにすると精度が出る傾向がありました。とりあえずここではOptunaを信頼して「$\lambda=0.43, \sigma=90$」という設定で試してみます。
細かい設定など。このようなCNNを使います。MNISTと同様にConvはConv→BN→ReLUとします。
| レイヤー | チャンネル数 | カーネル/Stride | 繰り返し |
|---|---|---|---|
| Conv | 64 | 3 | 3 |
| AvgPool | - | 2 | 1 |
| Conv | 128 | 3 | 3 |
| AvgPool | - | 2 | 1 |
| Conv | 256 | 3 | 3 |
| Global AvgPool | - | - | 1 |
| Batch Norm | - | - | 1 |
| Affinity loss | 10 | - | 1 |
- Affinity Lossは$m=1,5$を試した。$\sigma=90$, $\lambda=0.43$とする(Optunaでチューニング)。
- バッチサイズは640
- Weight Decayはなし
- MNISTの場合と同様に、テストデータを基準に1クラスあたりのサンプル数を500、200、100、50、20、10と変化させる。訓練データのサンプル数はテストデータの各5倍。
- TensorFlow/KerasのTPUで訓練する
- すべてのケースについて5回試行した
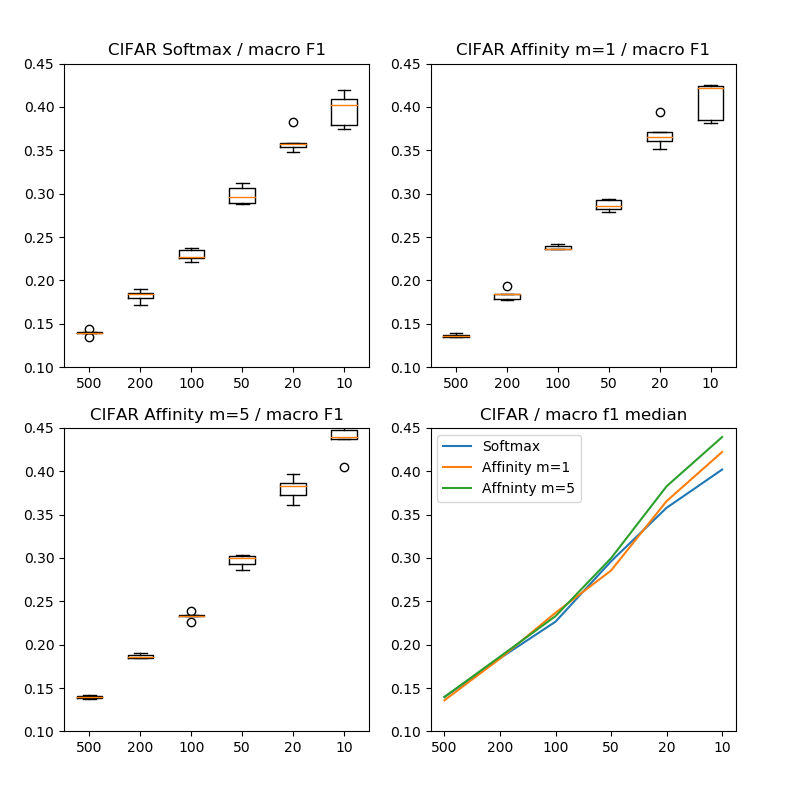
- Macro F1スコアで比較
CIFARの場合は、局所的にAffinity lossのほうが良いケースもあるも、全体的には効果が微妙でソフトマックスのほうが良かったケースも多かったです。なら「Affinity loss意味ないじゃん」と思うかも知れませんが、論文にかかれている結果を見ると、
LFWと、YTFというカラーの顔画像データセットにおいて非常に良い成績を収めているので、なぜCIFAR-10でうまく行かなかったのかがよくわからないというのが実情です(論文ではCIFAR-10についての言及がありませんでした)。
Affinity lossはデータセットの分布がある特定の状態で効果を発揮するのか、あるいはAffinity lossは本当はCIFAR-10でも効果を発揮するのだけれども自分の実験方法が悪いのか、2つの選択肢が考えられます。もし前者だった場合、Computer Visionの問題を解くのにMNISTのような簡単すぎるデータセットだけで検証するのはやはり問題があるのではないかと思います(論文に問題がある可能性がある)。Affinity lossは不均衡データに対して直感的には理解しやすいですが、汎用性があるのかどうかが、あるいはどういうデータセットに対して効果があるのか不明瞭な点が大きいことについてはかなり残念です。
追記:どうも別途で調べたところ、半分ぐらい後者でした。Data Augmentationをすると良くなります。 詳しくはこちら
「ソフトマックス」「Affinity m=1」、「Affinity m=5」の3パターンの各5回のF1スコアの中央値は次のようになります。
| サンプル数 | ソフトマックス | Affinity m=1 | Affinity m=5 |
|---|---|---|---|
| 500 | 86.03% | 86.41% | 86.03% |
| 200 | 81.57% | 81.61% | 81.38% |
| 100 | 77.35% | 76.32% | 76.71% |
| 50 | 70.39% | 71.45% | 70.03% |
| 20 | 64.22% | 63.45% | 61.74% |
| 10 | 59.81% | 57.78% | 56.06% |
実装上の注意点
自分がやってみてわかったポイントです。
普通のソフトマックスより学習が安定しないことがある。低次元の場合、初期値ガチャに鞍点に引っかかりやすい
これは仕方ないです。ガウス関数同士の足し引きをやっているので露骨な鞍点ができやすいのだと思います。Affinity lossの場合クラスタリングの中心点と、それぞれのそれぞれの点の更新を同時に行わないといけないので、相互的に学習が進んでくれる必要があります。初期値ガチャがかなり重要で、中心点が最初の段階で運悪くダブってしまうと、そこから抜け出すのにかなり時間がかかります。例えばこういうケース↓
このように中心点同士が近い場合は、損失関数上の鞍点になってしまい、学習が停滞することがありました。ただし、これはAdamなどの鞍点から抜け出しやすいオプティマイザーを使うとある程度は良くなります。論文ではモメンタムで実験していましたが、自分がやったらモメンタムではなかなか抜け出せなかったです。
また、初期値ガチャで最初に縦長/横長の偏ったプロットを引くとそこから抜け出すのがかなり大変になる(同じく鞍点挙動になる)ので、Affinity lossを入れる直前の層にBatch Noramlizationを入れることをおすすめします(特に低次元の場合)。Batch Normを入れたらかなりマシになりました。
→追記:あくまでこれは低次元限定なので、潜在空間が256次元のようなケースでは特に入れなくても悪化はしないようです。
ハイパーパラメータのチューニングが大変
CIFAR-10で実験してわかったのですが、かなりハイパーパラメータの選択($\lambda, \sigma, m$)が重要です。~~これだけチューニングしてCIFAR-10で1%効くかどうか、また副作用でかなり精度が下がることもある、というのは、もし一般的な画像データセットに対しても同じようなことになるのなら、自分としては残念ながら使うメリットはないのではないのかなと思います。~~逆にCIFAR-10で精度を出す方法があったらぜひ教えてほしいです。
追記:Data AugmentationをするとCIFAR-10でも良くなったので、とりあえず使ってみてもよいのではないでしょうか。ただし、評価尺度やデータによっては必ずしも良くなるというわけではないのでそこはあしからず。Softmaxのほうが良かったということもあります。不安ならSoftmaxと同時に訓練しても良いでしょう。追加の実験でこれを試しています。