DenseNetの論文を読んでみたのでまとめと、モデルを簡略化してCIFAR-10で実験してみた例を書きます。DenseNetはよくResNetとの比較で書かれますが、かなりわかりやすいアイディアなのが面白いです。
元の論文
G.Huang, Z.Liu, L.van der Maaten, K.Q.Weinberger. Densely Connected Convolutional Networks. IEEE Conference on Pattern Recognition and Computer Vision (CVPR), 2016.
https://arxiv.org/abs/1608.06993
DenseBlock
DenseNetとResNetの実装はとてもよく似ています。DenseNetの大きな特徴として「DenseBlock」というアイディアがあります。ResNetにも「ResBlock」というのがありますがどう違うのか見ていきます。
ResBlockとの違い
ResBlockの場合このようなショートカット構造を作りました[K.He et al.(2015)]。
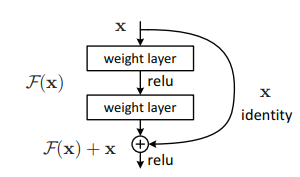
このぐるっと回っているのがショートカット側です。ショートカット側と対応して直線で進んでいる側をメイン側と呼ぶことにします。ResBlockの場合、メイン側で畳み込みを行い、ショートカット側はあくまでバイパスを作って以前のレイヤーにおける値を足すだけでした。
DenseBlockの場合ResBlockと逆で、ショートカット側で畳み込みを行います[G.Huang et al.(2016)]。

メイン側はショートカット側で得られたフィルターを重ねていくだけです。論文によると「メイン側は”The global state”と呼ばれ、そのグローバルな状態に対してDenseBlockが貢献していく」とあるため、ResNetになぞらえて捉えるのなら、ショートカット側で畳み込みをしていると考えるのが自然であるように思われます。
DenseBlockの図をResBlockになぞらえて書くと次のようになります。これはKerasでのDenseNet-121の実装になぞらえたものです。
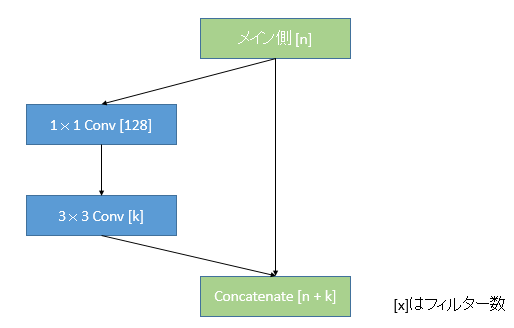
これが1つのDenseBlockです1。まずメイン側から分岐させ、1x1畳み込みを使ってフィルター数を一定(128)に統一させます。次に、3x3畳み込みでフィルター数をkとします。この**kをDenseNetでは成長率(Growth rate)**といいいます。最後に、k個のフィルターをメイン側に戻し、重ねる形で統合します。次のDenseBlockはnをn+kとしてまた分岐をはじめます。ResNetでは単純にフィルター数を増やしていくだけでしたが、DenseNetではフィルターを重ねていくのが大きな特徴です。
ボトルネック層による計算効率の上昇
論文では、1x1畳み込みを**ボトルネック層(Bottleneck layer)**と呼んでいます。分岐前のチャンネル数n次第では、n→128としたときにチャンネル数が増える場合減る場合の両方が考えられます。これは少なくとも「1x1→3x3畳み込みをする際のパラメーター数や計算量を頭打ちにする」、というメリットがあるは言えるでしょう。
なぜならいきなり3x3畳み込みをしてしまうと、nの値が大きくなるとパラメーター数がとても大きくなってしまうためです。例えばn=1024, k=32としましょう。(1)DenseNetの構造で畳み込みをする、(2)いきなり3x3の畳み込みをするの場合にわけてパラメーター数を計算します。
(1)DenseNetの構造の場合(1x1→3x3)
1x1畳み込み:1024×128 + 128 = 131,200
3x3畳み込み:128×32×3×3 + 32 = 36,896
合計:168,096
※Kerasの実装ではバイアスを使っていないのでパラメーター数の+128、+32は除外して考えても差し支えないです
(2)いきなり3x3畳み込みをする
合計:1024×32×3×3 + 32 = 294,944
1x1畳み込みによるボトルネック層を作ることで、パラメーター数を56%まで落とすことができました。このようにボトルネック層で一回フィルター数を頭打ちすることで、どんどん深くしていってnが大きくなった場合でも、パラメーター数が爆発的に増加しにくくなるメリットが得られます。
成長率(Growth rate)
説明が後回しになってしまいましたが、kの値は成長率と呼びます。ネットワーク上ではDenseBlock1つでどの程度フィルター数を増やすかというものです。論文ではより直感的な表現として、「知識の収集」と表現しています。
DenseBlockによりk個の特徴量のマッピングが追加されます。成長率はどの程度新しい情報をグローバルな状態(メイン側)に追加するのかをコントロールします。
DenseNet-121,169,201,264もすべて成長率のk=32としています。ただ、これはハイパーパラメータなので、他の値も設定することが可能です。論文ではkの値を変えて検証しています。
DenseBlockのKerasでの実装
KerasでのDenseNet-121の実装を参考に、1つのDenseBlockの実装を書き出してみます。
conv2_block1_concat (Concatenat (None, 56, 56, 96) 0 pool1[0][0]
conv2_block1_2_conv[0][0]
__________________________________________________________________________________________________
conv2_block2_0_bn (BatchNormali (None, 56, 56, 96) 384 conv2_block1_concat[0][0]
__________________________________________________________________________________________________
conv2_block2_0_relu (Activation (None, 56, 56, 96) 0 conv2_block2_0_bn[0][0]
__________________________________________________________________________________________________
conv2_block2_1_conv (Conv2D) (None, 56, 56, 128) 12288 conv2_block2_0_relu[0][0]
__________________________________________________________________________________________________
conv2_block2_1_bn (BatchNormali (None, 56, 56, 128) 512 conv2_block2_1_conv[0][0]
__________________________________________________________________________________________________
conv2_block2_1_relu (Activation (None, 56, 56, 128) 0 conv2_block2_1_bn[0][0]
__________________________________________________________________________________________________
conv2_block2_2_conv (Conv2D) (None, 56, 56, 32) 36864 conv2_block2_1_relu[0][0]
__________________________________________________________________________________________________
conv2_block2_concat (Concatenat (None, 56, 56, 128) 0 conv2_block1_concat[0][0]
conv2_block2_2_conv[0][0]
__________________________________________________________________________________________________
このConcat~Concatまでが1つのDenseBlockです。この例ではn=96、k=32です。96チャンネルの入力が、ボトルネック層により128チャンネルに統一され、3x3畳み込みで32チャンネルになり、それをメイン側に戻して96+32=128チャンネルとなるという形です。
Transition Layer
DenseNetはDenseBlockとTransitionLayerを交互に重ねていきます。TransitionLayerはとても簡単で1x1畳み込みと2x2のAveragePoolingをするだけです。1x1畳み込みではチャンネル数の圧縮を行います。この圧縮のパラメーター(Compression factor)は$\theta$で$0<\theta\leq 1$です。論文では$\theta=0.5$としています。
例えば、直前までのチャンネル数が256だった場合、この圧縮によりチャンネル数は128となります。また続くAveragePoolingにより解像度は半分にダウンサンプリングされます。DenseNet121のKerasでの実装を見ると、Transition Layerは次のようになっています。
pool2_relu (Activation) (None, 56, 56, 256) 0 pool2_bn[0][0]
__________________________________________________________________________________________________
pool2_conv (Conv2D) (None, 56, 56, 128) 32768 pool2_relu[0][0]
__________________________________________________________________________________________________
pool2_pool (AveragePooling2D) (None, 28, 28, 128) 0 pool2_conv[0][0]
__________________________________________________________________________________________________
Global Average Pooling
DenseNetはチャンネル単位で積み重ねていくため、全結合化するときにFlattenではなく**Global Average Pooling(GAP)**を使います。
参考:https://qiita.com/mine820/items/1e49bca6d215ce88594a
今簡単な例として、2x2のチャンネルが3個あったとしましょう。
\begin{align}
A_1=\left[\begin{array}{r} 1 & 2 \\ 3 & 4 \end{array}\right], A_2=\left[\begin{array}{r} 5 & 6 \\ 7 & 8 \end{array}\right],
A_3=\left[\begin{array}{r} 9 & 10 \\ 11 & 12 \end{array}\right]
\end{align}
もしこれを全結合化した場合、出力は$\left[\begin{array}{r}1,2,\cdots,12 \end{array}\right]$となります。GAPの場合チャンネル単位での平均を取り、全結合化します。チャンネル単位での平均は$A_1=2.5, A_2=6.5, A_3=10.5$となります。したがって、GAPでの出力は$\left[\begin{array}{r}2.5, 6.5, 10.5 \end{array}\right]$となります。
GAPを使うとチャンネル数が減るため、全結合層でのパラメーター数やオーバーフィッティングが解消されるというメリットがあります。DenseNetの場合はより直感的に、「情報をチャンネル単位で積み重ねているのだから、Flattenでチャンネルの内の個々の値を使うより、GAPでチャンネル単位での平均を取ったほうがより自然」というのは理解しやすいです。
DenseNetの全貌
これまでのアイディアをまとめて、DenseNetの全体の実装を確認します。
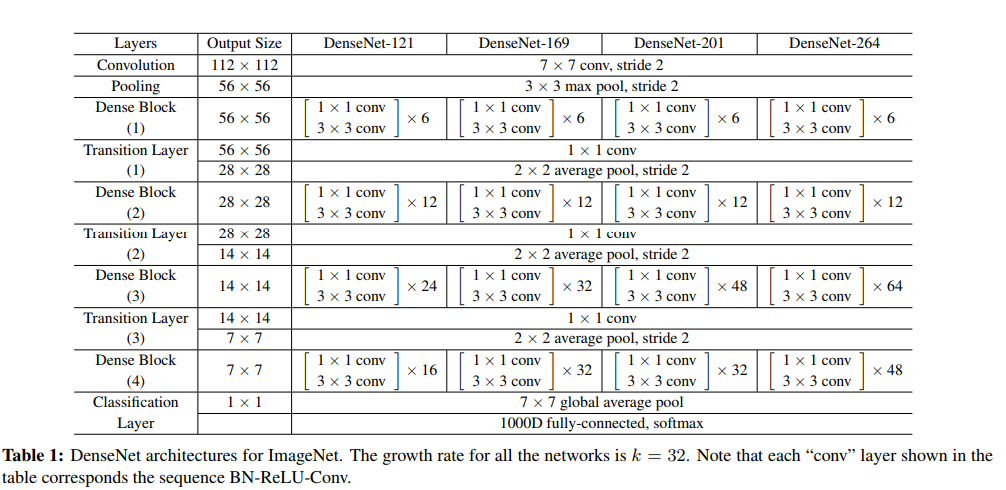
論文からのものですが、このように「DenseBlock(s)→Transition→DenseBlock(s)→…」と交互に重ねていくのがDenseNetの全体の構造です。DenseBlockの層で×6、×12とありますがこれは1x1→3x3畳み込みからなるDenseBlockを6個、12個重ねるよという意味です。
自分で実装してみる(コード)
DenseNetのアイディアはとてもわかりやすいので、サクッとかけました。CIFAR-10で確認してみます。論文に示されているDenseNet-BCの実装がわかればよかったのですがよくわからなかったので、DenseNet121を参考に成長率とDenseBlockの反復回数を変えて軽いモデルを作ってみました。
from keras.layers import Conv2D, Activation, BatchNormalization, Concatenate, AveragePooling2D, Input, GlobalAveragePooling2D, Dense
from keras.models import Model
from keras.optimizers import Adam
from keras.datasets import cifar10
from keras.utils import to_categorical
from keras.preprocessing.image import ImageDataGenerator
import pickle
import numpy as np
class DenseNetSimple:
def __init__(self, growth_rate, compression_factor=0.5, blocks=[1,2,4,3]):
# 成長率(growth_rate):DenseBlockで増やすフィルターの数
self.k = growth_rate
# 圧縮率(compression_factor):Transitionレイヤーで圧縮するフィルターの比
self.compression = compression_factor
# モデルの作成
self.model = self.make_model(blocks)
# DenseBlockのLayer
def dense_block(self, input_tensor, input_channels, nb_blocks):
x = input_tensor
n_channels = input_channels
for i in range(nb_blocks):
# 分岐前の本線
main = x
# DenseBlock側の分岐
x = BatchNormalization()(x)
x = Activation("relu")(x)
# Bottle-Neck 1x1畳み込み
x = Conv2D(128, (1, 1))(x)
x = BatchNormalization()(x)
x = Activation("relu")(x)
# 3x3畳み込み フィルター数は成長率
x = Conv2D(self.k, (3, 3), padding="same")(x)
# 本線と結合
x = Concatenate()([main, x])
n_channels += self.k
return x, n_channels
# Transition Layer
def transition_layer(self, input_tensor, input_channels):
n_channels = int(input_channels * self.compression)
# 1x1畳み込みで圧縮
x = Conv2D(n_channels, (1, 1))(input_tensor)
# AveragePooling
x = AveragePooling2D((2, 2))(x)
return x, n_channels
# モデルの作成
def make_model(self, blocks):
# blocks=[6,12,24,16]とするとDenseNet-121の設定に準じる
input = Input(shape=(32,32,3))
# 端数を出さないようにフィルター数16にする
n = 16
x = Conv2D(n, (1,1))(input)
# DenseBlock - TransitionLayer - DenseBlock…
for i in range(len(blocks)):
# Transition
if i != 0:
x, n = self.transition_layer(x, n)
# DenseBlock
x, n = self.dense_block(x, n, blocks[i])
# GlobalAveragePooling(チャンネル単位の全平均)
x = GlobalAveragePooling2D()(x)
# 出力層
output = Dense(10, activation="softmax")(x)
# モデル
model = Model(input, output)
return model
# 訓練
def train(self, X_train, y_train, X_val, y_val):
# コンパイル
self.model.compile(optimizer=Adam(), loss="categorical_crossentropy", metrics=["acc"])
# Data Augmentation
datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=20,
width_shift_range=0.2,
height_shift_range=0.2,
channel_shift_range=50,
horizontal_flip=True)
# 訓練
#history = self.model.fit(X_train, y_train, batch_size=128, epochs=1, validation_data=(X_val, y_val)).history
# 水増しありの訓練
history = self.model.fit_generator(datagen.flow(X_train, y_train, batch_size=128),
steps_per_epoch=len(X_train) / 128, validation_data=(X_val, y_val), epochs=1).history
# 保存
with open("history.dat", "wb") as fp:
pickle.dump(history, fp)
if __name__ == "__main__":
# k=16の場合
densenet = DenseNetSimple(16)
# densenet.model.summary()
# CIFAR-10の読み込み
(X_train, y_train), (X_test, y_test) = cifar10.load_data()
# X_train = (X_train / 255.0).astype("float32")
X_test = (X_test / 255.0).astype("float32")
y_train, y_test = to_categorical(y_train), to_categorical(y_test)
densenet.train(X_train, y_train, X_test, y_test)
DenseNet121との違いは、最初のDenseBlockに入る前の導入部分プーリング層とパディング層を除外しています。最初から1x1畳み込みをしてチャンネル数を16にしてから即DenseBlockに入ります。
DenseNet121の成長率k=32であるのに対して、このサンプルではk=16としています(コンストラクタでいじれます)。また、DenseNet121ではDenseBlockをblocks=[6, 12, 24, 16]で重ねましたが、この例では**各値を6で割り[1, 2, 4, 3]**としました(これもコンストラクタのオプションでいじれます)。今回いろいろ変えて遊んでみるのは、成長率k、ブロック構造のblocksの2つです。
ちなみにモデルの深さは、DenseBlockでは1つのブロックにつき1x1と3x3の2回畳み込みをすること、Transitionでは1x1の1回、導入部分でも1x1の1回、出力層でSoftmaxのDenseを1回することを踏まえると、
$$\rm{Depth}=\sum_{i=0}^{n_b-1}(\rm{blocks[i]}*2) + n_b +1 $$
で表されます。ここで$n_b$はDenseBlock→Transitionの反復回数で、DenseNetでは$n_b=4$です。blocks=[6,12,24,16]の場合、2(6+12+24+16)+4+1=121でDenseNet121の121と等しくなります*。この例ではblocks=[1,2,4,3]なので、モデルの深さは2*(1+2+4+3)+5=25層であるといえます。
ちなみにk=16、blocks=[1,2,4,3]でのパラメーター数は以下の通りです。
Total params: 255,046
Trainable params: 251,614
Non-trainable params: 3,432
パラメーター数はたった25万です。これはモデルが小さいこともありますが、1x1畳み込みを活用してパラメーター数を抑えられているのが大きなポイントです。
kとblockの値を変えてCIFAR-10で簡単に実験してみます。
結果
(1)k=16, blocks=[1,2,4,3], Data Augmentation(水増し)なしの場合
パラメーター総数:255,046、深さ:25
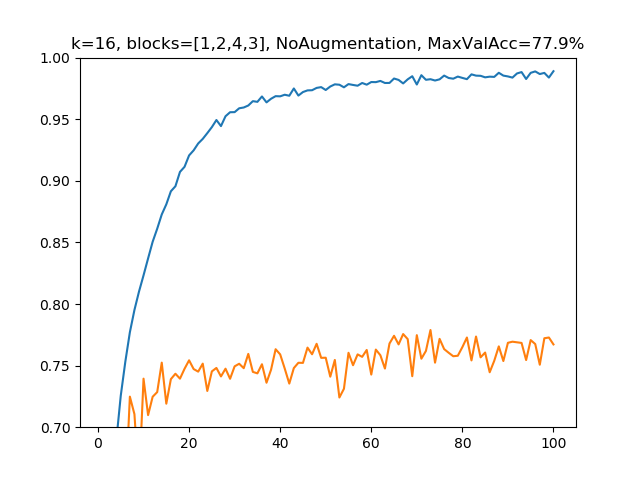
水増しなしだとオーバーフィッティングするのは相変わらず。論文ではもっと深いモデルに対して、水増ししたケースとしなかったケース両方調べていましたが、水増しをしなくても重み減衰やドロップアウトをチューニングしてあげるともう少しよくなると思います。
(2)k=16, blocks=[1,2,4,3], 水増しありの場合
パラメーター総数:255,046、深さ:25
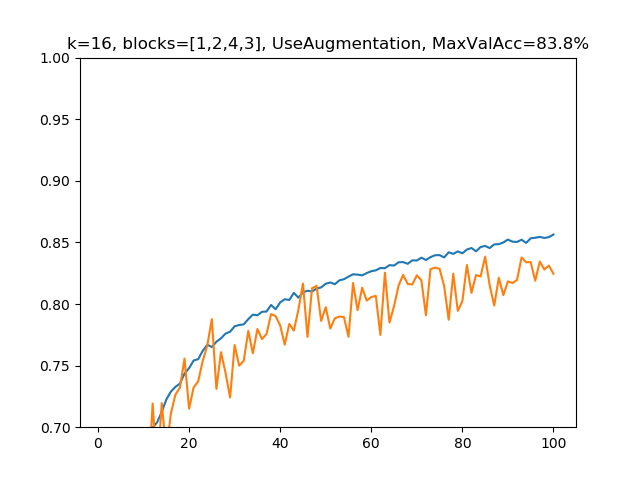
水増しの処理は上記のコードによるものです。ここでの水増し処理はすべて共通のものを使っています。
すごくわかりやすく正則化効果が出ています。ドロップアウトもなしに強すぎるぐらい正則化が効いているので、成長率kを小さな値に制限することでオーバーフィッティングしづらくなっているというのがわかります。
(3)k=32, blocks=[1,2,4,3], 水増しありの場合
パラメーター総数:505,200、深さ:25
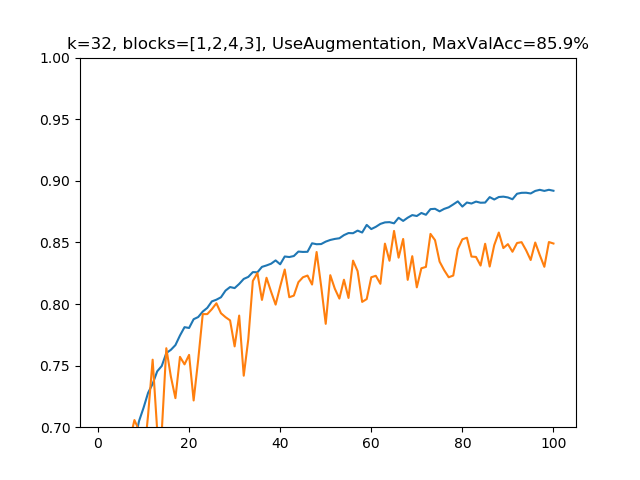
深さは変えずに成長率を倍にしてみました。パラメーター総数はおおよそ倍になっています。モデルを大きくすればオーバーフィッティングしやすくなるので、正則化の副作用は軽減されています。(2)と比べて精度は2.1%上がりました。
後で示しますが、訓練の計算時間はKeras+GPU(Google Colab)の場合、kを増やすことよりもモデルを深くすることのほうが強く比例します。これはモデルを深くした場合それに伴ってボトルネック層の1x1畳み込みが増えるため(kを増やした場合は増えない)かと思われます。
(4)k=16, blocks=[2,4,8,5], 水増しありの場合
パラメーター総数:599,536、深さ:43
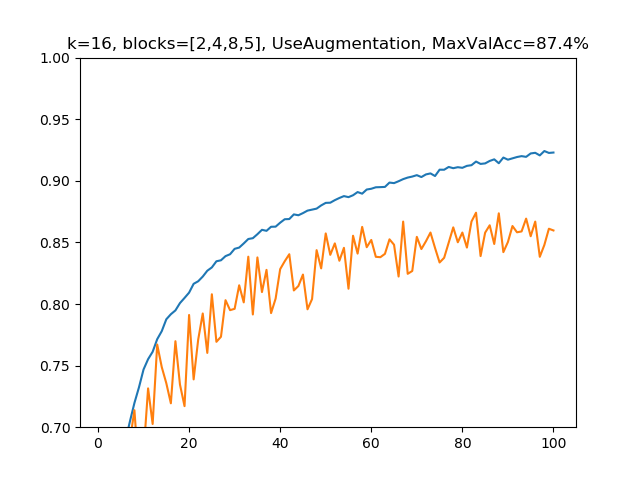
今度はk=16に戻してモデルを深くします。この場合は、パラメーター数は(3)とあまり変わりませんが、(2)→(3)でパラメーター数を倍にしたのに準じるぐらいの精度上昇(2.1%)が、(3)→(4)で見られます(1.5%)。100epoch程度なので誤差の範囲かもしれませんが、(3)→(4)で計算時間は倍近くになっているのでそれとのトレードオフと考えるとそこまで不思議ではないです。
(5)k=16, blocks=[3,6,12,8], 水増しありの場合
パラメーター総数:1,104,186、深さ:63
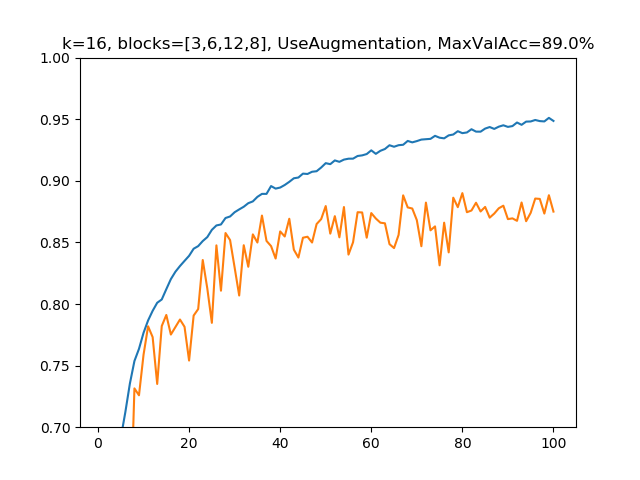
さらに深くしました。若干オーバーフィッティングが目立つようになりましたが、(4)よりも1.6%精度上昇しました。
(6)k=16, blocks=[6,12,24,16], 水増しありの場合
パラメーター総数:3,316,848、深さ:121
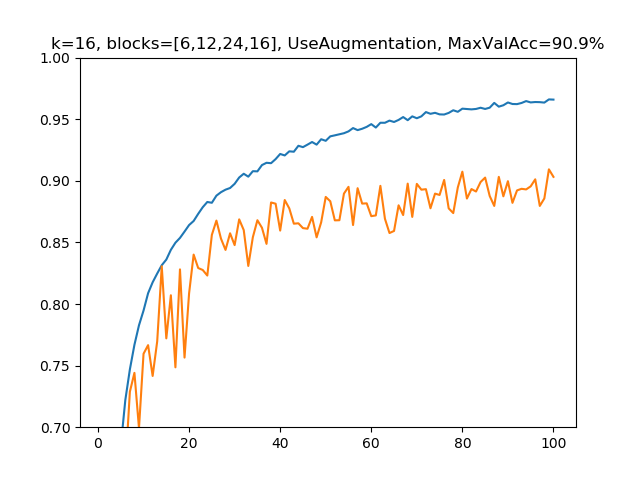
もっと深くして、DenseNet-121とほぼ同じセッティングになりました。この場合では(5)よりもさらに精度は1.9%上昇し、明確に90%の大台を突破しました。
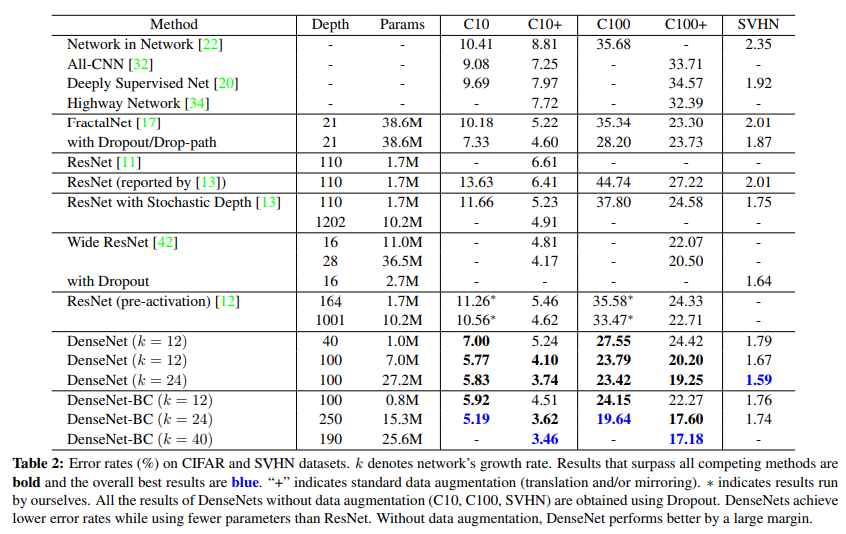
論文ではもっとドロップアウトや重み減衰などの他の正則化手段を使いCIFAR-10に対し、k=12のDenseNetで、水増しなしで7.00%のエラー率、水増しありで5.24%のエラー率を達成したとあります。DenseNet-BC(通常のDenseNetとの違いがいまいちわからないけど1x1畳み込みのボトルネック層を置くか置かないか?)ではk=12で、5.92%/4.51%。k=24のDenseNet-BCは5.19%/3.62%だそうです。なので、もっとちゃんとチューニングすればあと5%は精度の上乗せできると思います。
ただし、(6)のケースではGPUで1epochに5分ぐらいかかって訓練が結構大変になってきます。計算速度についても見ておきます。
計算速度
各6(5パターン)について5epochの計算速度(秒)を求めました。環境はGoogle ColabのGPUで、Kerasのバージョンは2.1.6です。
| No | k | blocks | 平均[*] | epoch1 | epoch2 | epoch3 | epoch4 | epoch5 |
|---|---|---|---|---|---|---|---|---|
| 1/2 | 16 | [1,2,4,3] | 64.7 | 75.3 | 63.5 | 63.5 | 64.9 | 65.9 |
| 3 | 32 | [1,2,4,3] | 67.1 | 78.8 | 65.8 | 66.3 | 66.9 | 68.1 |
| 4 | 16 | [2,4,8,5] | 116.3 | 134.3 | 114.1 | 118.2 | 115.0 | 115.7 |
| 5 | 16 | [3,6,12,8] | 175.2 | 197.3 | 174.7 | 175.1 | 175.1 | 175.5 |
| 6 | 16 | [6,12,24,16] | 381.8 | 430.4 | 381.7 | 381.8 | 381.7 | 381.7 |
コード全体はこちら:https://gist.github.com/koshian2/70fe027d789c2181e7f9127924afa1af
平均は、5epochのうち最大と最小を除いた3つの平均です。どれも1epoch目は若干時間がかかる傾向があります。ここで興味深いのは、kを増やしてもそこまで計算時間は増えないのに、モデルの深さ(blocks)を増やすとほぼ定数倍に近い形で計算時間が増えるということです。DenseBlockの構造を振り返ると、kを増やしてもボトルネックの1x1畳み込みは増えないが、深くするとその分だけボトルネックが増えるからということがありかと思います。
ちなみにパラメーターの数はkを増やしてもblockを増やしてもどちらも定数倍に近い形で増えます。つまり、kを増やすかモデルを深くするかということは、時間と空間のトレードオフの調整が容易にできるということです。論文には示されていませんでしたが、ここの調整が簡単にできるのがDenseNetの強みではないかなと個人的に思います。
例えば、GPUのメモリは少ないが計算性能(FLOPS)はそこそこある場合、kを削って深くすればいいですし、逆にメモリは潤沢にあるが計算速度を上げたい場合はkを大きくしてモデルを浅くすればいいのではないでしょうか。ただ、(3)と(4)で見る限りでは、パラメーター数が似たような状態では、kが大きく浅いモデルよりも、kが小さく深いモデルのほうがモデルの表現力はおそらく高いと思います。それはニューラルネットワーク全般に言えることで、モデルの深さに対して指数関数的に表現力が増えるからということと関連しているように考えられます。
まとめ
これまでの結果をまとめます。
| No | k | blocks | 水増し | epoch | パラメーター数 | 深さ | MaxValAcc | 計算時間 |
|---|---|---|---|---|---|---|---|---|
| 1 | 16 | [1,2,4,3] | no | 100 | 255,046 | 25 | 77.9% | - |
| 2 | 16 | [1,2,4,3] | yes | 100 | 255,046 | 25 | 83.8% | 64.7 |
| 3 | 32 | [1,2,4,3] | yes | 100 | 505,200 | 25 | 85.9% | 67.1 |
| 4 | 16 | [2,4,8,5] | yes | 100 | 599,536 | 43 | 87.4% | 116.3 |
| 5 | 16 | [3,6,12,8] | yes | 100 | 1,104,186 | 63 | 89.0% | 175.2 |
| 6 | 16 | [6,12,24,16] | yes | 100 | 3,316,848 | 121 | 90.9% | 381.8 |
DenseNetの特徴は次の点にあると思います。
・DenseBlockでフィルター数を適宜減らしているため、ドロップアウトを使わなくても強い正則化効果がある
これは論文にも書かれていたことで、論文によると『DenseNetはネットワーク全体での情報と勾配のフローの改善している。各層は損失関数と元の入力信号からの勾配に直接アクセスでき、暗黙の深い教師につながる。これは、より深いネットワークアーキテクチャの訓練に役立つ。さらに、密度の高い接続には正則化効果があり、トレーニングセットのサイズを小さくしてタスクのオーバーフィットを軽減できる。』とあります。
層の積み重ねが正則化に寄与しているのかは自分がやった実験では確認できませんでしたが、成長率のkを小さな値に設定することでオーバーフィッティングを解消するというのは、ドロップアウトと似たようにニューロンの数を小さくする効果があるので、正則化効果があるのは納得しやすいものでした。CNNによる画像認識ではBiasよりも、Varianceのほうが問題となることが多いので、今回確認したようにモデルを深くしてもそこまでオーバーフィッティングが深刻にならないのは便利かなと思いました。
・パラメーター数が深さの割に少ない
これも半ば当たり前で、1x1畳み込みをうまく活用して、パラメーター数を増えないように工夫しています。論文では計算量についてはResNetとの比較のみ行われていましたが、InceptionシリーズやInceptionResNetと比べたときにどうなのか?というのは書かれていませんでした。
ここからは自分の感想ですが、1x1畳み込みがパラメーター削減に寄与している一方で、今回確認したように深くすればするほど計算時間がめりめり増えていくという事実があります。もしかするとDenseBlockの1x1畳み込みのフィルター数を128で固定にしてしまったのが問題だったのかもしれませんね。いくらダイレクトに3x3畳み込みをしないとはいっても、1x1畳み込みの入力側のフィルター数が144を超えると1x1畳み込みの側の計算量のほうが支配的になるので2、深くすればするほどDenseBlockの数の1x1分だけ余計なコストを払う必要があります。他の100層超えのネットワークも訓練してみないとなんともいえませんが、計算量については若干疑問の残る結果となりました。
・ 成長率とブロック構成でコントロールする原理がわかりやすい
これがいいポイントだなと自分は思いました。Googleが最近出したNASNetのようにネットワークの構成をハンドデザインではなく、強化学習で決めさせるというアプローチがだんだん増えていくと思います。このNASNetを見ると、確かに精度は出てるのだけれども、とても構成が複雑で「なぜそんなデザインになったのか」と聞いても「強化学習の結果そうなりました」としか多分答えてくれないと思います。
その一方でDenseNetを見ると、成長率のkで「獲得する知識の量」をコントロールし、ブロック構成で「モデルの深さ」をコントロールする。前者は主にパラメーター数に影響し、後者はパラメーター数と計算量に大きく影響するから、あとはハードウェア制約を加味してkと深さをコントロールすればよい、という原理的にはとても単純です。より直感的には、フィルターの積み重ねつまり「知識の集積」をして、GAPで平均を取って分類するというのが人間的には理解しやすいなと個人的に思いました。
以上、DenseNetの論文を読んでモデル構成を変えてCIFAR-10で実装してみることで、だいたいのイメージを掴んでみました。DenseNetの本質的な「知識の獲得」や「過去の累積して知識の共有」というところまではなかなか踏み込めませんでしたが、皆さんの理解に役立てば幸いです。
-
論文ではこのショートカット構造を集合体をDenseBlockと呼んでいますが、ここではResBlockとの対比でわかりやすいようにショートカット構造1つをDenseBlockと呼ぶことにします ↩
-
FLOPSとは厳密には異なるかもしれませんが、Conv2dでの計算量は簡易的に「縦の解像度×横の解像度×入力チャンネル数×出力チャンネル数×縦のカーネル数×横のカーネル数」で表すことができます。padding=sameなので、1x1畳み込みと3x3畳み込みの解像度は同じです。3x3畳み込み側の入力チャンネル(128)×出力チャンネル(k=16)×縦のカーネル(3)×横のカーネル(3)と、1x1畳み込み側の入力チャンネル(x)×出力チャンネル(128)×縦横のカーネル(1)を比較しxを解くと「144」と求められます。 ↩