高校数学で理解する逆強化学習（その１）

はじめに

逆強化学習 (Inverse Reinforcement Learning; IRL) が注目されている。強化学習は、問題と報酬（の条件）があたえらたときに、報酬を最大化する行動方策を学習する問題だが、逆強化学習は問題と報酬を最大化する行動方策が与えられたときに報酬（の条件）を推定する。この方法を発展させることで、熟練者の行動サンプルを元に問題を解くのに適した行動方策を学習する師弟学習などに繋がってゆく。

この記事では、3回にわけて、逆強化学習の始祖的存在である Ng and Russel, "Algorithms for Inverse Reinforcement Learning" をステップバイステップで説明してゆく。
（というより自分が読んだときの理解を残しておく）

その1では3章の説明をのせる。

• その1: 離散有限空間において最適な方策が与えられたときのIRL（第3章）
• その2: 連続空間において最適な方策が与えられたときのIRL (第4章)
• その3: 連続空間において熟練者の行動例が与えられたときのIRL (第5章)

制限事項（言い訳）

私は別に強化学習の専門家ではない。あくまでも最近強化学習に手をだしはじめたので理解した内容を書き下しているだけである。したがって間違えがあるかもしれない。

「高校数学で」などと吹かしたが、前提知識に強化学習の話が必要だったりするので、あくまでも逆強化学習について、簡単な線形代数まで落とした説明だと思ってくれると嬉しい。

高校数学で読み解く逆強化学習（その１）

前提

論文にのっとり、報酬は行動ではなく状態だけからきまるものとする。これを状態・行動からきまる報酬関数に拡張するのは自明（らしい、ためしてないけど）のため。

ベルマン方程式、ベルマンの最適性については内容を理解しているものとして説明しない¹。後ほど参照するので、下記に論文化からベルマン方程式とベルマンの最適性の原理を載せておく。

ベルマン方程式

状態$S = \{s_1, s_2, ...\}$、行動$A = \{a_1, a_2, ...\}$、遷移関数$P_{sa}(s')$ （状態sで行動aをとったときにs'に遷移する確率）、割引率$\gamma$、報酬関数$R: S \rightarrow ℝ$からなるマルコフ決定過程（MDP）と、方策$\pi: S \rightarrow A$ が与えられた時、価値関数$V^\pi$とQ関数$Q^\pi$は式(1)と式(2)を満たす。

(1)

$$
V^\pi(s) = R(s) + \gamma\sum_{s'}P_{s\pi(s)}(s')V^\pi(s')
$$

(2)

$$
Q^\pi(s, a) = R(s) + \gamma\sum_{s'}P_{sa}(s')V^\pi(s')
$$

ベルマンの最適性の原理

状態$S$、行動$A$、遷移関数$P_{sa}(s')$、割引率$\gamma$、報酬関数$R$からなるMDPが与えられた時、すべての$s \in S$ に対して式(3)が成り立つとき、そして成り立つときのみ$\pi$は最適な方策である。

(3)

$$
\pi(s) \in \arg\max_{a \in A}Q^\pi(s, a)
$$

式番号(1)などは論文内の記述と整合性をとってある。本記事で補足式を出す場合は(i)のような形で表記する。

離散有限空間において最適な方策が与えられたときのIRL

まず1個目の問題設定は、有限かつ離散的な空間が与えられた時に、最適な方策が与えられたとき、報酬関数を推定するものである。例えば、グリッド内で上下左右にしかいけない世界を考えるとわかりやすい。

• 入力：最適な方策 $\pi^*: S \rightarrow A$
• 出力：報酬関数 $R: S \rightarrow ℝ$

報酬関数が満たすべき条件 (3.1節）

p. 3のTheorem 3を導出しよう。この定理をしめすことで、与えらたMDPにぴったしハマるような報酬はどのような性質を満たさないといけないかがわかる。

式(1)は、次のように書ける。

(i)

$$
\mathbf{V}^\pi = \mathbf{R} + \gamma\mathbf{P}_{\pi^*}\mathbf{V}^\pi
$$

ここで、

• $\mathbf{V}^\pi$ は、$|S|$行 (状態の数) の行列で、行 $i$ は状態 $s_i$ における価値関数の値 $V^\pi(s_i)$ を示す。
• $\mathbf{R}$ は $|S|$ 行の行列で、行$i$は状態$s_i$における報酬を示す。
• $\mathbf{P}_a$ は $|S|$ 行 $|S|$ 列の行列で、行 $i$ 列 $j$ は、行動 $a$ をとったときに状態 $s_i$ から状態 $s_j$ に遷移する確率を示す。
• $\mathbf{P}_{\pi^*}$ は $|S|$ 行 $|S|$ 列の行列で、行 $i$ 列 $j$ は、最適な方策 $\pi^*$ に基づいて行動したときに状態 $s_i$ から状態 $s_j$ に遷移する確率を示す。

つまり、各状態 $s_i$ についてばらばらにかかれていた連立方程式を、1つの行列の式にまとめただけである。

論文では上記の $\mathbf{P}_{\pi^*}$ に相当する表記として、$\mathbf{P}_{a_1}$ という表記を使っている。しかし、これはある 単一の行動$a_1$をとったときの遷移確率をしめしているのではなく、上記で説明したとおり最適な方策 $\pi^*$ に基づいて行動したときの遷移確率を示している²。本記事では、わかりやすさのために、$\mathbf{P}_{\pi^*}$ を使う。

式(i)から$\mathbf{V}^\pi$を左辺に移動し、式(5)を算出する。

(5)

$$
\mathbf{V}^\pi = (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{R}
$$

p. 3中部の式を順番にみてゆく。式(3)に式(4)を導入し式(ii)を得る。

(ii)

$$
\pi^*(s) = \arg\max_{a \in A} \sum_{s'}P_{sa}(s')V^\pi(s') \qquad \forall s \in S
$$

ここで、$R(s)$ と $\gamma$ は $a$ と関係がない（入っていてもargmaxの結果は変わらない）ので、消えている。

argmaxの定義から、$\pi^*(s)$ は他のすべての $a$ よりも、argmax内の項が大きいはずなので、左辺に$\pi^*(s)$の場合、右辺にそれ以外の行動をとった場合を並べて、

(iii)

$$
\sum_{s'}P_{s\pi^*(s)}(s')V^\pi(s') \geq \sum_{s'}P_{sa}(s')V^\pi(s') \qquad \forall s \in S, \forall a \in A\backslash\pi^*(s)
$$

式(i)を組み立てたのと同様の行列化によって、(iii)の $\forall s \in S$ の部分を行列にすると、

(iv)

$$
\mathbf{P}_{\pi^*}\mathbf{V}^\pi \succeq \mathbf{P}_a\mathbf{V}^\pi \qquad \forall a \in A\backslash\pi^*(s)
$$

$\succeq$ は要素ごとの不等号 $\geq$ を示しており、行列の全要素が不等号 $\geq$ をみたしてることを意味する。$\mathbf{P}$ の各行は各状態における遷移確率を示しているが、前述したとおり行ごとにとっている行動も異なることに注意する。

式(iv)に式(5)を代入し、整理することで、式(4)を得る。

(4)

$$
(\mathbf{P}_{\pi^*} - \mathbf{P}_a) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{R} \succeq 0 \qquad \forall a \in A\backslash\pi^*(s)
$$

報酬関数の最適化（3.2節）

さて、上記で報酬関数$R$が満たすべき条件はわかったが、これだけでは意味のある報酬関数が得られたとは言えない。たとえば、$\mathbf{R}$の全要素が0であっても、式(4)は満たされる。

そこで、目的関数を次の式の最大化にかえる。

(v)

$$
\sum_{s \in S} \left( Q^\pi(s, \pi^*(s)) - \max_{a \in A \backslash \pi^*(s)} Q^\pi(s, a) \right) - \lambda \|\mathbf{R}\|_1
$$

$\max_{a \in A \backslash \pi^*(s)} Q^\pi(s, a)$ は 2番目に良い行動における報酬 を示す。つまりこの式は全体として常に2番目の行動よりも良い行動を選べる方策を探索している。2項目の $- \lambda \|\mathbf{R}\|_1$ は報酬関数が可能な限りシンプルになるようにかける正則化である。（行動中の色々なところでバラバラと報酬を与えるより、1つの「ゴール」にて大きな報酬を与える報酬関数を好む。）

$Q^\pi(s, \pi^*(s)) - \max Q^\pi(s, a)$ は $\min \left( Q^\pi(s, \pi^*(s)) - Q^\pi(s, a) \right)$ と等価なので、これらをまとめると、最終的には次の式の最大化として定式化できる。

(vi)

$$
\sum_i\min_{a \in A \backslash\pi^*(s_i)} \left\{(\mathbf{P}_{\pi^*}(i) - \mathbf{P}_{a}(i)) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{R} \right\} - \lambda \|\mathbf{R}\|_1
$$

s.t.

$$
(\mathbf{P}_{\pi^*} - \mathbf{P}_a) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{R} \succeq 0 \qquad \forall a \in A\backslash\pi^*(s)
$$

$$
0 \preceq \mathbf{R} \preceq R_{max}
$$

ただし、$\mathbf{P}_{\pi^*}(i)$は$\mathbf{P}_{\pi^*}$の$i$行目をさしている。要は、前述したとおり行ごとに、$\pi^*(s_i)$ の行動が異なるため、行ごとに $\min_{a \in A \backslash\pi^*(s_i)}$ を求め、そのあとにすべての行の和をとっている。報酬は $\mathbf{R}$ の絶対値を大きくしてゆけば無限に大きくなってしまうため、$R_{max}$ を使い上から押さえている。

例

ここまでで、本問題設定を最適化問題としての定式化することができた。そこで、考えられる中でもっとも簡単な例で、逆強化学習を行う。

問題設定

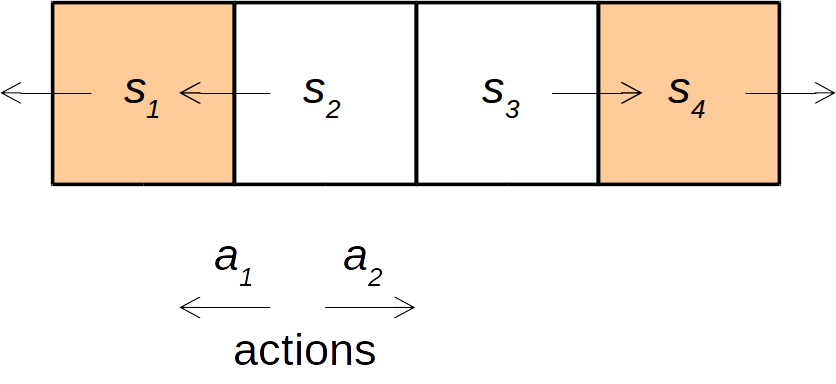
次のような1次元グリッドの世界が存在するとする。この世界では左端のグリッド（$s_1$)か、右端のグリッド ($s_4$) にたどり着くと報酬がもらえる（逆強化学習側からはこの報酬の情報は使えない）。また、遷移確率は決定的であるとする（つまり、状態$s_2$から左に行動 ($a_1$) すれば、必ず状態 $s_1$になる）。

$\gamma = 0.5$とする。

この問題における最良の方策は次のとおりである。この方策は与えられているとする。

• 状態1ならば状態1へ $\pi(s_1) = a_1$
• 状態2ならば状態1へ $\pi(s_2) = a_1$
• 状態3ならば状態4へ $\pi(s_3) = a_2$
• 状態4ならば状態4へ $\pi(s_4) = a_2$

逆強化学習の実行

最良の方策に従っている場合、たとえば状態2からの遷移確率は次のようになる。

\mathbf{P}_{\pi^*(s_2)}(2) = \mathbf{P}_{a_1}(2) = \left[
\begin{array}{cccc}
      1 & 0 & 0 & 0 
\end{array}\right]

今回行動は2パターンしかないため、最良の行動がわかれば、最良の行動の次に良い行動もきまる。状態2から最良の行動の次に良い行動をとったの遷移確率は次のようになる。

\mathbf{P}_{s_2a_2} = \left[
\begin{array}{cccc}
      0 & 0 & 1 & 0 
\end{array}\right]

これを各状態に行うことで、式(vi)を簡単に書き下すことができる。

\min_{a \in A \backslash\pi^*(s)} \left((\mathbf{P}_{s\pi^*(s)} - \mathbf{P}_{sa}) (\mathbf{I} - \gamma\mathbf{P}_{s\pi^*(s)})^{-1} \mathbf{R} \right) \\
= \left(\left[\begin{array}{cccc}
    1 & 0 & 0 & 0 \\
    1 & 0 & 0 & 0 \\
    0 & 0 & 0 & 1 \\
    0 & 0 & 0 & 1  
\end{array}\right] - \left[\begin{array}{cccc}
    0 & 1 & 0 & 0 \\
    0 & 0 & 1 & 0 \\
    0 & 1 & 0 & 0 \\
    0 & 0 & 1 & 0  
\end{array}\right]\right) \left(\left[\begin{array}{cccc}
    1 & 0 & 0 & 0 \\
    0 & 1 & 0 & 0 \\
    0 & 0 & 1 & 0 \\
    0 & 0 & 0 & 1  
\end{array}\right] - \gamma\left[\begin{array}{cccc}
    1 & 0 & 0 & 0 \\
    1 & 0 & 0 & 0 \\
    0 & 0 & 0 & 1 \\
    0 & 0 & 0 & 1 
\end{array}\right]\right)^{-1} \left[\begin{array}{c}
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4)
\end{array}\right] \\
= \left[\begin{array}{cccc}
    1 & -1 & 0 & 0 \\
    1 & 0 & -1 & 0 \\
    0 & -1 & 0 & 1 \\
    0 & 0 & -1 & 1  
\end{array}\right] \left[\begin{array}{cccc}
    2 & 0 & 0 & 0 \\
    1 & 1 & 0 & 0 \\
    0 & 0 & 1 & 1 \\
    0 & 0 & 0 & 2  
\end{array}\right] \left[\begin{array}{c}
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4)
\end{array}\right] \\
= \left[\begin{array}{cccc}
    1 & -1 & 0 & 0 \\
    2 & 0 & -1 & -1 \\
    -1 & -1 & 0 & 2 \\
    0 & 0 & -1 & 1  
\end{array}\right] \left[\begin{array}{c}
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4)
\end{array}\right]

以上より、最適化問題は次のとおりである。

\underset{\mathbf{R}}{\text{maximize}} \sum\left[\begin{array}{cccc}
    1 & -1 & 0 & 0 \\
    2 & 0 & -1 & -1 \\
    -1 & -1 & 0 & 2 \\
    0 & 0 & -1 & 1  
\end{array}\right] \left[\begin{array}{c}
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4)
\end{array}\right] -  \lambda \|\mathbf{R}\|_1

s.t.

\left[\begin{array}{cccc}
    1 & -1 & 0 & 0 \\
    2 & 0 & -1 & -1 \\
    -1 & -1 & 0 & 2 \\
    0 & 0 & -1 & 1  
\end{array}\right] \left[\begin{array}{c}
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4)
\end{array}\right] \succeq 0

0 \preceq \mathbf{R} \preceq R_{max}

これを、$R_{max} = 1$, $\lambda = 0.5$ としてとくと、解は $\mathbf{R} = [1, 0, 0, 1]$である。

ちなみに、論文でも述べられているが$\lambda$は十分大きければ良好な（シンプルな）報酬を与えるが、$\lambda$には臨界点$\lambda^-_0$がある。今回は$\lambda^-_0 = 1.0$ が臨界点であり、このとき自明解$\mathbf{R} = [0, 0, 0, 0]$も解の1つとなる。

IRLの効率的な最適化

以上までではIRLがどのように定式化可能なのかを説明した。しかし、上記例でもわかるが、状態・行動の数が増えてゆくと、手で解くのは加速的にむずかしくなってゆく。

そこで、式(vi)を計算機を使って効率的に解く方法を考えたい。式(vi)とその条件はすべて一次連立不等式の形をしているため、論文内にもかかれているとおり線形計画法 (Linear Programming) を使うことで効率的に解くことができる。

線形計画法の概要については他の文献に譲るが、応用面からいえば連立一次不等式を式(vii)の形に整理し、ソルバー³にいれることで高速に最適化をしてくれるものだ。

(vii)

\underset{\mathbf{x}}{\text{minimize}}\quad \mathbf{c}^T\cdot\mathbf{x}

\text{s.t.}\quad\mathbf{A}\cdot\mathbf{x} \preceq \mathbf{b}

ただし、$\mathbf{A}$は行列、$\mathbf{c}$と$\mathbf{b}$は行ベクトルである。

それでは、式(vi)を式(vii)の形に整理してみよう。⁴

まず、トリックとして、

(viii)

(\mathbf{P}_{\pi^*} - \mathbf{P}_a) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{R} \succeq \mathbf{T} \qquad a \in A \backslash\pi^*(s_i)

なる $\mathbf{T}$ をおく。この $\mathbf{T}$ は常に左辺より小さくなるため、$\min_{a \in A \backslash\pi^*(s_i)} \left\{(\mathbf{P}_{\pi^*}(i) - \mathbf{P}_{a}(i)) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{R}\right\}$ の部分を表現することができる。

また、$\|\cdot\|_1$は線形計画法でうまく表現できないので、 式(ix)を満たす $u$ で$\|\mathbf{R}\|_1 $ を置き換える。本来 $\|\cdot\|_1$ は絶対値の和だが、 $\mathbf{R}$ の全要素は制約から常に非負なので、式(ix)だけで十分である。

(ix)

\sum \mathbf{R} \preceq u

式(viii)と式(ix)をおくことで、式(vi)は次のように整理される。(maximizeだったのを符号を逆にすることでminimizeにしている。)

(x)

\underset{\mathbf{x}}{\text{minimize}}\quad  -\sum_i \mathbf{T}  + \lambda u 

s.t.

(\mathbf{P}_{\pi^*} - \mathbf{P}_a) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{R} \succeq \mathbf{T} \qquad a \in A \backslash\pi^*(s_i)

$$
(\mathbf{P}_{\pi^*} - \mathbf{P}_a) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{R} \succeq 0 \qquad \forall a \in A\backslash\pi^*(s)
$$

$$
0 \preceq \mathbf{R} \preceq R_{max}
$$

\sum \mathbf{R} \preceq u

ここで、 $\mathbf{T}$、 $\|\mathbf{R}\|_1$ 、 $\mathbf{R}$ は式内に$\mathbf{R}$を含んでいるため、これらを未知の値 $\mathbf{x}$ とおく。

(xi)

\underset{\mathbf{x}}{\text{minimize}}\quad \left[\begin{array}{c}
    -1 \\
    0  \\
    \lambda
\end{array}\right]^T \left[\begin{array}{c}
    \mathbf{T} \\
    \mathbf{R} \\
    u
\end{array}\right]

s.t.

\left[\begin{array}{c}
    1 \\
    -(\mathbf{P}_{\pi^*} - \mathbf{P}_a) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1}   \\
    0
\end{array}\right]^T\left[\begin{array}{c}
    \mathbf{T} \\
    \mathbf{R} \\
    u
\end{array}\right] \preceq  0  \qquad \forall a \in A\backslash\pi^*(s)

\left[\begin{array}{c}
    0 \\
    -(\mathbf{P}_{\pi^*} - \mathbf{P}_a) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1}   \\
    0
\end{array}\right]^T\left[\begin{array}{c}
    \mathbf{T} \\
    \mathbf{R} \\
    u
\end{array}\right] \preceq  0  \qquad \forall a \in A\backslash\pi^*(s)

\left[\begin{array}{c}
    0 \\
    -1  \\
    0
\end{array}\right]^T\left[\begin{array}{c}
    \mathbf{T} \\
    \mathbf{R} \\
    u
\end{array}\right] \preceq 0

\left[\begin{array}{c}
    0 \\
    1  \\
    0
\end{array}\right]^T\left[\begin{array}{c}
    \mathbf{T} \\
    \mathbf{R} \\
    u
\end{array}\right] \preceq R_{max}

\left[\begin{array}{c}
    0 \\
    [1 \quad 1 \quad ...]  \\
    -1
\end{array}\right]^T\left[\begin{array}{c}
    \mathbf{T} \\
    \mathbf{R} \\
    u
\end{array}\right] \preceq 0

制約式をすべて結合して大きな行列$\mathbf{A}$ を作れば完成だ。

例

最適化手法についても前述した例で同様に考えてみる。まず、この問題設定にあわせて$\mathbf{x}$を書き下さす。

(xii)

\mathbf{x} = \left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4) \\
    u
\end{array}\right]

式(xii)をもとに式(xi)に上記でもとめたパラメータを当てはめてゆく。

(xiii)

\underset{\mathbf{x}}{\text{minimize}}\quad \left[\begin{array}{c}
     -1\\
     -1 \\
     -1 \\
     -1 \\
     0\\
     0\\
     0 \\
     0\\
     \lambda
\end{array}\right]^T\left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4) \\
    u
\end{array}\right] 

s.t.

\left[\begin{array}{cccc}
     1 & 0 & 0 & 0\\
     0 & 1 & 0 & 0\\
     0 & 0 & 1 & 0 \\
     0 & 0 & 0 & 1 \\
    -1 &-2 & 1 & 0\\
     1 & 0 & 1 & 0\\
     0 & 1 & 0 & 1\\
     0 & 1 &-2 &-1\\
     0 & 0 & 0 & 0
\end{array}\right]^T\left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4) \\
    u
\end{array}\right] \preceq \left[\begin{array}{c}
    0 \\
    0 \\
    0 \\
    0 
\end{array}\right] 

\left[\begin{array}{cccc}
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0 \\
    -1 &-2 & 1 & 0\\
     1 & 0 & 1 & 0\\
     0 & 1 & 0 & 1\\
     0 & 1 &-2 &-1\\
     0 & 0 & 0 & 0
\end{array}\right]^T\left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4) \\
    u
\end{array}\right] \preceq \left[\begin{array}{c}
    0 \\
    0 \\
    0 \\
    0 
\end{array}\right] 

\left[\begin{array}{cccc}
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0 \\
    -1 & 0 & 0 & 0\\
     0 &-1 & 0 & 0\\
     0 & 0 &-1 & 0 \\
     0 & 0 & 0 &-1 \\
     0 & 0 & 0 & 0
\end{array}\right]^T\left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4) \\
    u
\end{array}\right] \preceq \left[\begin{array}{c}
    0 \\
    0 \\
    0 \\
    0 
\end{array}\right] 

\left[\begin{array}{cccc}
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0 \\
     1 & 0 & 0 & 0\\
     0 & 1 & 0 & 0\\
     0 & 0 & 1 & 0 \\
     0 & 0 & 0 & 1 \\
     0 & 0 & 0 & 0
\end{array}\right]^T\left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4) \\
    u
\end{array}\right] \preceq \left[\begin{array}{c}
    R_{max} \\
    R_{max} \\
    R_{max} \\
    R_{max} 
\end{array}\right] 

\left[\begin{array}{c}
     0\\
     0 \\
     0 \\
     0 \\
     1\\
     1\\
     1 \\
     1 \\
    -1
\end{array}\right]^T\left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4) \\
    u
\end{array}\right] \preceq \left[\begin{array}{c}
    0 
\end{array}\right] 

2つ目の制約式は $a \in A \backslash\pi^*(s_i)$ という表記を1つの行列して表す。$\mathbf{T}$ は1つの行動あたり状態の数$|S|$ 分の大きさを持つため、右辺は$(|A| - 1)$ 行$|S|$列の行列を持つことになる。

\left[\begin{array}{ccccccccc}
     1 & 0 & 0 & 0 &-1 & 1 & 0 & 0 & 0\\
     0 & 1 & 0 & 0 &-2 & 0 & 1 & 1 & 0\\
     0 & 0 & 1 & 0 & 1 & 1 & 0 &-2 & 0\\
     0 & 0 & 0 & 1 & 0 & 0 & 1 &-1 & 0\\
     0 & 0 & 0 & 0 &-1 & 1 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 &-2 & 0 & 1 & 1 & 0\\
     0 & 0 & 0 & 0 & 1 & 1 & 0 &-2 & 0\\
     0 & 0 & 0 & 0 & 0 & 0 & 1 &-1 & 0\\
     0 & 0 & 0 & 0 &-1 & 0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 & 0 &-1 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 & 0 & 0 &-1 & 0 & 0\\
     0 & 0 & 0 & 0 & 0 & 0 & 0 &-1 & 0\\
     0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\
     0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\
     0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 &-1\\
 \end{array}\right] \left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    R(s_1) \\
    R(s_2) \\
    R(s_3) \\
    R(s_4) \\
    u
\end{array}\right]
 \preceq \left[\begin{array}{c}
    0 \\
    0 \\
    0 \\
    0 \\
    0 \\
    0 \\
    0 \\
    0 \\
    0 \\
    0 \\
    0 \\
    0 \\
    R_{max} \\
    R_{max} \\
    R_{max} \\
    R_{max} \\
    0 \\    
\end{array}\right] 

\mathbf{c} = \left[\begin{array}{c}
     -1\\
     -1 \\
     -1 \\
     -1 \\
     0\\
     0\\
     0 \\
     0\\
     0.5
\end{array}\right]

導出した行列を実際に線形計画法にいれてみよう。($\gamma = 0.5$, $\lambda = 0.5$, $R_{max} = 1.0$ が代入してある。)

import numpy as np
from scipy.optimize import linprog

c = np.array([-1, -1, -1, -1, 0, 0, 0, 0, 0.5])
A = np.array([
    [1, 0, 0, 0,-1, 1, 0, 0, 0],
    [0, 1, 0, 0,-2, 0, 1, 1, 0],
    [0, 0, 1, 0, 1, 1, 0,-2, 0],
    [0, 0, 0, 1, 0, 0, 1,-1, 0],
    [0, 0, 0, 0,-1, 1, 0, 0, 0],
    [0, 0, 0, 0,-2, 0, 1, 1, 0],
    [0, 0, 0, 0, 1, 1, 0,-2, 0],
    [0, 0, 0, 0, 0, 0, 1,-1, 0],
    [0, 0, 0, 0,-1, 0, 0, 0, 0],
    [0, 0, 0, 0, 0,-1, 0, 0, 0],
    [0, 0, 0, 0, 0, 0,-1, 0, 0],
    [0, 0, 0, 0, 0, 0, 0,-1, 0],
    [0, 0, 0, 0, 1, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 1, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 1, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 1, 0],
    [0, 0, 0, 0, 1, 1, 1, 1,-1],
], dtype=np.float)
b = np.array(
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,  1,  1,  1, 1, 0],   
    dtype=np.float)

linprog(c, A, b)

結果

     fun: -3.0
 message: 'Optimization terminated successfully.'
     nit: 7
   slack: array([ 0.,  0.,  0.,  0.,  1.,  1.,  1.,  1.,  1.,  0.,  0.,  1.,  0.,
        1.,  1.,  0.,  0.])
  status: 0
 success: True
       x: array([ 1.,  1.,  1.,  1.,  1.,  0.,  0.,  1.,  2.])

解として、$\mathbf{R} = [1, 0, 0, 1]$ が得られ、正しく報酬の情報を捉えられていることがわかる。

少活

離散的な空間において、最適な方策が与えらた時に、報酬関数を推定する方法について説明した。しかし、実際には多くの実問題は離散空間とはいえないし、最適な方策が得られることは現実的な問題ではまずありえない。

その2 では、その1で説明した離散空間における逆強化学習を連続空間に拡張し（第４章）、その3では最適な方策のかわりにいくつかの行動サンプルが与えらたときの逆強化学習方法(第5章)について説明する。

参考文献

• Ng and Russel, "Algorithms for Inverse Reinforcement Learning", ICML, 2010.
• @neka-nat@github, "逆強化学習を理解する", Qiita, Retrieved on 25th/Apr/2018.

1. 適当にググれば良い説明がみつかる。個人的にはQ学習（DQNではない）を実装してみると理解しやすいと思う。 ↩

2. 論文内ではこの処置は表記の簡便さのためとしている。p.2の "By renaming actions if necessary, we will assume ... $\pi(s) \equiv a_1$" というところで、$a_1$ は添字を変えながらも常にある状態における最適な方策に基づく行動を示すもの としている。正直わかりにくい.... ↩

3. Pythonからさっと使えるものだったらscipy.optimize.linprog とか。 ↩

4. この部分は@neka-nat@githubさんによる"逆強化学習を理解する"を丸パク参考にさせていただいている。素晴らしい記事に感謝申し上げたい。 ↩