LoginSignup
10
16

More than 5 years have passed since last update.

@koreyou(Yuta Koreeda)

高校数学で理解する逆強化学習（その2）

Posted at

はじめに

逆強化学習 (Inverse Reinforcement Learning; IRL) が注目されている。強化学習は、問題と報酬（の条件）があたえらたときに、報酬を最大化する行動方策を学習する問題だが、逆強化学習は問題と報酬を最大化する行動方策が与えられたときに報酬（の条件）を推定する。この方法を発展させることで、熟練者の行動サンプルを元に問題を解くのに適した行動方策を学習する師弟学習などに繋がってゆく。

この記事では、3回にわけて、逆強化学習の始祖的存在である Ng and Russel, "Algorithms for Inverse Reinforcement Learning" をステップバイステップで説明してゆく。
（というより自分が読んだときの理解を残しておく）

その2では4章の説明をのせる。

本記事はその1を前提としている。
式番号(1)などは論文内の記述と整合性をとってある。本記事で補足式を出す場合は(i)のような形で表記する。番号はその1からの通し番号としている。

連続空間において最適な方策が与えられたときのIRL

2個目の問題設定は、連続的な空間において、有限の行動、最適な方策が与えられたとき、報酬関数を推定するものである。

  • 入力：最適な方策 $\pi^*: S \rightarrow A$
  • 出力：報酬関数 $R: S \rightarrow ℝ$

高校数学で理解する逆強化学習（その１） で導出した、報酬関数が満たすべき条件 (3.1節）を再掲する。

(4)

$$
(\mathbf{P}_{\pi^*} - \mathbf{P}_a) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{R} \succeq 0 \qquad \forall a \in A\backslash\pi^*(s)
$$

  • $\mathbf{V}^\pi$ は、$|S|$行 (状態の数) の行列で、行 $i$ は状態 $s_i$ における価値関数の値 $V^\pi(s_i)$ を示す。
  • $\mathbf{R}$ は $|S|$ 行の行列で、行$i$は状態$s_i$における報酬を示す。
  • $\mathbf{P}_a$ は $|S|$ 行 $|S|$ 列の行列で、行 $i$ 列 $j$ は、行動 $a$ をとったときに状態 $s_i$ から状態 $s_j$ に遷移する確率を示す。
  • $\mathbf{P}_{\pi^*}$ は $|S|$ 行 $|S|$ 列の行列で、行 $i$ 列 $j$ は、最適な方策 $\pi^*$ に基づいて行動したときに状態 $s_i$ から状態 $s_j$ に遷移する確率を示す。
  • $\gamma$ は強化学習における割引率である。

つまり式(4)は各行で「状態」を表現していたが、連続空間においては無限の「状態」が存在するため、行列の形で書き下すことはできない。そこで、論文では次の工夫をすることで、連続空間におけるIRLを行列の形で書き下すことを提案している。

  1. 行にすべての状態 $S$ を書き下すのではなく、サンプリングした状態 $S_0$ を用いる。
  2. 報酬$\mathbf{R}$を、行列ではなく状態の特徴量の線型結合で表す。

2は、具体的には次の関数のように表現する。

\mathbf{R} = \alpha_1 \phi_1(s_i) + \alpha_2 \phi_2(s_i) + \alpha_3 \phi_3(s_i) + ...

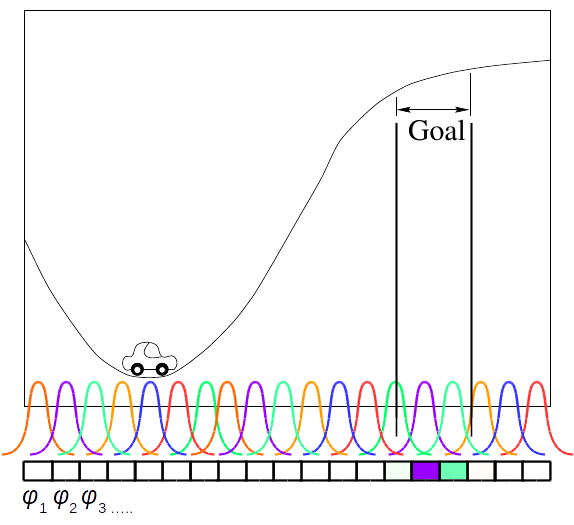
$\phi(s)$は状態の特徴量である。論文内の実験では、等間隔に配置したガウス分布を基底の特徴量としていた。

reward-digitalization.png

連続空間において最適な方策が与えられたときのIRLの目的関数を式(ix)に示す。これその1と全く同じで、１番良い方策と時点で良い方策の差が最大にすることを示している。

(ix)

\underset{\mathbf{x}}{\text{maximize}}\quad \sum_{s \in S_0}\min_{a \in A \backslash\pi^*(s)} p \left(\mathbb{E}_{s' \sim P_{s \pi^*(s_i)}}[V^\pi(s')] - \mathbb{E}_{s' \sim P_{sa}}[V^\pi(s')]\right)

離散有限空間において最適な方策が与えられたときのIRLにおける目的関数（式(vi)）には、その1に存在した条件（$(\mathbf{P}_{\pi^*} - \mathbf{P}_a) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{R} \succeq 0$ が存在しないことに注意する。これは、連続空間では$\mathbf{R}$が近似に過ぎないため、この条件が必ずしも満たされるとは限らないからである1。かわりに、本問題設定では、式(x)に示す$p$を使い、条件が満たされない場合にペナルティを与えることで条件式を緩和している。

(x)

    p(x)= 
\begin{cases}
    x,  & x\geq 0\\
    \eta x, & \text{otherwise}
\end{cases}

論文内では、 $\eta$ の値は結果にあまり影響を与えないと報告されており、値として $\eta = 2$ を使用したとあった。

IRLの効率的な最適化

論文内では式(ix)までで説明が終わっているが、実際にこれを線形計画法の問題にまで落としてみよう。

まず、式(ix)、ある状態の価値関数の期待値を、サンプルした状態における価値関数の和で表現しよう。

(xi)

\mathbb{E}_{s' \sim P_{sa}}[V^\pi(s')] \approx \sum_{s'}P_{sa}(s')V^\pi(s')

式(x)はある状態$s$に対する価値関数であるため、右辺をサンプルした状態$s \in S_0$ について並べて、式(xii)のように再定義する。

(xii)

\left[\begin{array}{c}
    \mathbb{E}_{s' \sim P_{s_1a}}[V^\pi(s')] \\
    \mathbb{E}_{s' \sim P_{s_2a}}[V^\pi(s')] \\
    \vdots
\end{array}\right] \equiv \mathbf{P}_{a} \mathbf{V}^\pi

式(5)を多少の変数の乱用だが本問題に流用する。なお、式(xii)があれば、その1にしめした証明と全く同じ証明で式(5)が成り立つことを示すことができる。

(5)

$$
\mathbf{V}^\pi = (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{R}
$$

離散空間の問題において、$\mathbf{V}^\pi$ は全状態を行に並べたものだったが、今回はサンプルした $s \in S_0$ を行に並べる。$\mathbf{P}_{\pi^*}$ も同様に、サンプルした状態を対象に$\pi^*$から作成する。

(xiii)

\mathbf{R} = \left[\begin{array}{ccc}
    \phi_1(s_1) & \phi_2(s_1) & \cdots \\
    \phi_1(s_2) & \phi_2(s_2) & \cdots \\
    \vdots & \vdots & \ddots  
\end{array}\right] \cdot \left[\begin{array}{cc}
    \alpha_1 \\
    \alpha_1 \\
    \vdots
\end{array}\right] \equiv \mathbf{\Phi} \mathbf{\alpha}

式(ix)、式(xii)、式(5)を組みわせて、目的関数として式(xiv)を得る。

(xiv)

\underset{\mathbf{x}}{\text{maximize}}\quad  \sum_i \min_{a \in A \backslash\pi^*(s_i)} p \left((\mathbf{P}_{\pi^*}(i) - \mathbf{P}_{a}(i)) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{\Phi}\mathbf{\alpha} \right) \\

$$
\text{s.t.}\quad |\mathbf{\alpha}| \preceq 1
$$

ただし、$\mathbf{P}_{\pi^*}(i)$は$\mathbf{P}_{\pi^*}$の$i$行目をさしている。要は、前述したとおり行ごとに、$\pi^*(s_i)$ の行動が異なるため、行ごとに $\min_{a \in A \backslash\pi^*(s_i)}$ を求め、そのあとにすべての行の和をとっている。報酬は $\mathbf{R}$ の絶対値を大きくしてゆけば無限に大きくなってしまうため、$|\mathbf{\alpha}|$ を上から押さえている。

(その1)で行ったように $min$ を表現するために、式(xv)なる $\mathbf{T}$ をおく。

(xv)

p\left((\mathbf{P}_{\pi^*} - \mathbf{P}_a) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{\Phi} \mathbf{\alpha}\right) \succeq \mathbf{T} \qquad a \in A \backslash\pi^*(s_i)

また、関数$p$を表現するために式(xvi)と式(xvii)で式(xv)を表現する。

(xvi)

(\mathbf{P}_{\pi^*} - \mathbf{P}_a) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{\Phi} \mathbf{\alpha} = \mathbf{T}^+ - \mathbf{T}^-\\
  \qquad \forall a \in A\backslash\pi^*(s)

(xvii)

\mathbf{T}^+ - 2 \mathbf{T}^- \succeq \mathbf{T}   \qquad \forall a \in A\backslash\pi^*(s)

式(xvi)は$p$の条件わけを示している。つまり、右辺のi行目が0より大きい場合は$\mathbf{T}^-$のi行目は0になる。右辺のi行目が0より小さい場合は$\mathbf{T}^+$のi行目は0になる。

同様に、$\mathbf{\alpha}$の定義域を0以上に拡大するために、$\mathbf{\alpha}$を式(xviii)とおく(線形計画法はすべての変数が正であることを仮定するため）。

(xviii)

\mathbf{\alpha}^+ - \mathbf{\alpha}^- = \mathbf{\alpha}\\
1 \succeq \mathbf{\alpha}^+ \succeq 0 \\
1 \succeq \mathbf{\alpha}^- \succeq 0

式(xiii)、式(xvi)と式(xvii)を用いることで、式(xiv)は次のように整理される。(maximizeだったのを符号を逆にすることでminimizeにしている。)

(xiv)

\underset{\mathbf{x}}{\text{minimize}}\quad  -\sum_i \mathbf{T}

s.t. $\forall a \in A\backslash\pi^*(s)$

\mathbf{V}_{diff} (\mathbf{\alpha}^+ - \mathbf{\alpha}^-) = \mathbf{T}^+ - \mathbf{T}^-

\mathbf{T}^+ - 2 \mathbf{T}^- \succeq \mathbf{T}

1 \succeq \mathbf{\alpha}^+ \succeq 0

1 \succeq \mathbf{\alpha}^- \succeq 0

where

\mathbf{V}_{diff} = (\mathbf{P}_{\pi^*} - \mathbf{P}_a) (\mathbf{I} - \gamma\mathbf{P}_{\pi^*})^{-1} \mathbf{\Phi}

ここで、 $\mathbf{T}$、 $\mathbf{T}^+$ 、 $\mathbf{T}^-$ 、 $\mathbf{\alpha}^+$ 、 $\mathbf{\alpha}^-$ 、 $\mathbf{m}$ を未知の値 $\mathbf{x}$ とおく。

(xix)a

\underset{\mathbf{x}}{\text{minimize}}\quad \left[\begin{array}{c}
    -1 \\
    0  \\
    0  \\
    0  \\
    0
\end{array}\right]^T \left[\begin{array}{c}
    \mathbf{T} \\
    \mathbf{T}^+ \\
    \mathbf{T}^- \\
    \mathbf{\alpha}^+ \\
    \mathbf{\alpha}^-
\end{array}\right]

s.t. $\forall a \in A\backslash\pi^*(s)$

(xix)b

\left[\begin{array}{c}
    0  \\
    -1 \\
    1  \\
    \mathbf{V}_{diff} \\
    -\mathbf{V}_{diff}\\
    0
\end{array}\right]^T\left[\begin{array}{c}
    \mathbf{T} \\
    \mathbf{T}^+ \\
    \mathbf{T}^- \\
    \mathbf{\alpha}^+ \\
    \mathbf{\alpha}^-
\end{array}\right] =  0

(xix)c

\left[\begin{array}{c}
    1  \\
    -1 \\
    \eta  \\
    0 \\
    0
\end{array}\right]^T\left[\begin{array}{c}
    \mathbf{T} \\
    \mathbf{T}^+ \\
    \mathbf{T}^- \\
    \mathbf{\alpha}^+ \\
    \mathbf{\alpha}^-
\end{array}\right] \preceq 0

(xix)d

\left[\begin{array}{c}
    0  \\
    0  \\
    0  \\
    1  \\
    0
\end{array}\right]^T\left[\begin{array}{c}
    \mathbf{T} \\
    \mathbf{T}^+ \\
    \mathbf{T}^- \\
    \mathbf{\alpha}^+ \\
    \mathbf{\alpha}^-
\end{array}\right] \preceq 1

(xix)e

\left[\begin{array}{c}
    0  \\
    0  \\
    0  \\
    0  \\
    1
\end{array}\right]^T\left[\begin{array}{c}
    \mathbf{T} \\
    \mathbf{T}^+ \\
    \mathbf{T}^- \\
    \mathbf{\alpha}^+ \\
    \mathbf{\alpha}^-
\end{array}\right] \preceq 1

(xix)f

\left[\begin{array}{c}
    \mathbf{T} \\
    \mathbf{T}^+ \\
    \mathbf{T}^- \\
    \mathbf{\alpha}^+ \\
    \mathbf{\alpha}^-
\end{array}\right] \succeq 0

制約式をすべて結合して大きな行列$\mathbf{A}$ を作れば完成だ。

例

ここまでで、本問題設定を最適化問題としての定式化することができた。そこで、考えられる中でもっとも簡単な例で、逆強化学習を行う。

問題設定

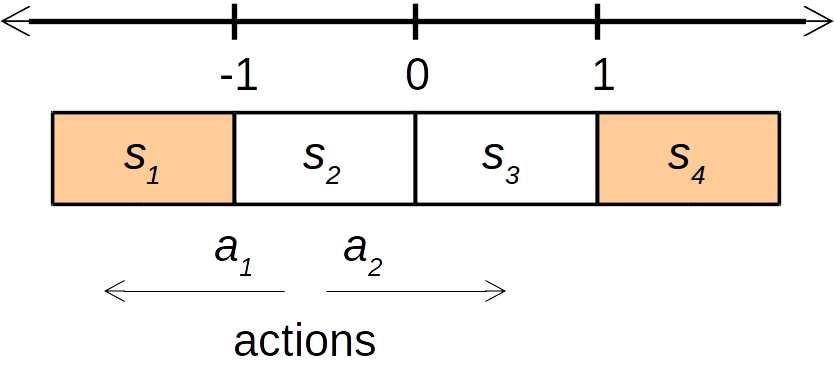
次のような1次元の世界 $s \in ℝ$ が存在するとする。この世界では、$s \leq -1$か$s \geq 1$ にたどりつくと報酬がもらえる（逆強化学習側からはこの報酬の情報は使えない）。行動は左に1進む ($a_1$) か、左に1進む ($a_2$) かだけである。また、遷移確率は決定的であるとする（つまり、状態$s = 0.5$から左に行動 ($a_1$) すれば、必ず状態 $s = -0.5$になる）。

example2.png

$\gamma = 0.5$とする。

この問題における最良の方策は次のとおりである。この方策は与えられているとする。

  • 状態が$s \geq 0$ならば右へ
  • 状態が$s < 0$ならば左へ

(xx)

\pi(s) = \begin{cases}
a_1, & if s \le 0\\
a_2  & \text{otherwise}
\end{cases}

逆強化学習の実行

まず、状態の特徴量 $\mathbf{\Phi}$ を設定する。ここでは、最も簡単なグリッドを使ってしまう。2

(xxi)

\phi_1(s) = \begin{cases}
  1, & if s \leq -1 \\
  0  & \text{otherwise}
\end{cases} \\
\phi_2(s) = \begin{cases}
  1, & if -1 < s < 0 \\
  0  & \text{otherwise}
\end{cases} \\
\phi_3(s) = \begin{cases}
  1, & if 0 \leq s < 1 \\
  0  & \text{otherwise}
\end{cases} \\
\phi_4(s) = \begin{cases}
  1, & if 1 \leq s \\
  0  & \text{otherwise}
\end{cases}

3つの状態をサンプルする。ここでは、簡単のため4つの状態、 $s_1 = -0.3$ 、 $s_2 = -1.3$ 、 $s_3 = 0.7$ 、 $s_3 = 1.7$を考える。3 最良の方策に従っている場合、たとえば状態$s_1 = -0.3$からの遷移確率は次のようになる。

\mathbf{P}_{\pi^*(s_1)}(1) = \mathbf{P}_{a_1}(1) = \left[
\begin{array}{cccc}
      0 & 1 & 0 & 0 
\end{array}\right]

今回行動は2パターンしかないため、最良の行動がわかれば、最良の行動の次に良い行動もきまる。状態1から最良の行動の次に良い行動をとったの遷移確率は次のようになる。

\mathbf{P}_{s_2a_2} = \left[
\begin{array}{cccc}
      0 & 0 & 1 & 0 
\end{array}\right]

これを各状態に行い、式(xxi)を導入することで、式(xix)を書き下すことができる。

(xxii)

\min_{a \in A \backslash\pi^*(s)} \left((\mathbf{P}_{s\pi^*(s)} - \mathbf{P}_{sa}) (\mathbf{I} - \gamma\mathbf{P}_{s\pi^*(s)})^{-1} \mathbf{\Phi} \mathbf{\alpha} \right) \\
= \left(\left[\begin{array}{cccc}
    0 & 1 & 0 & 0 \\
    0 & 0 & 0 & 0 \\
    0 & 0 & 0 & 1 \\
    0 & 0 & 0 & 0  
\end{array}\right] - \left[\begin{array}{cccc}
    0 & 0 & 1 & 0 \\
    1 & 0 & 0 & 0 \\
    1 & 0 & 0 & 0 \\
    0 & 0 & 1 & 0  
\end{array}\right]\right) \left(\left[\begin{array}{cccc}
    1 & 0 & 0 & 0 \\
    0 & 1 & 0 & 0 \\
    0 & 0 & 1 & 0 \\
    0 & 0 & 0 & 1  
\end{array}\right] - \gamma\left[\begin{array}{cccc}
    0 & 1 & 0 & 0 \\
    0 & 0 & 0 & 0 \\
    0 & 0 & 0 & 1 \\
    0 & 0 & 0 & 0  
\end{array}\right]\right)^{-1} \left[\begin{array}{cccc}
    0 & 1 & 0 & 0 \\
    1 & 0 & 0 & 0 \\
    0 & 0 & 1 & 0 \\
    0 & 0 & 0 & 1  
\end{array}\right] \left[\begin{array}{c}
    \alpha_1 \\
    \alpha_2 \\
    \alpha_3 \\
    \alpha_4
\end{array}\right] \\
= \left[\begin{array}{cccc}
     0 & 1 & -1 & 0 \\
    -1 & 0 &  0 & 0 \\
    -1 & 0 &  0 & 1 \\
     0 & 0 & -1 & 0  
\end{array}\right] \left[\begin{array}{cccc}
    1 & 0.5 & 0 & 0 \\
    0 & 1 & 0 & 0 \\
    0 & 0 & 1 & 0.5 \\
    0 & 0 & 0 & 1  
\end{array}\right] \left[\begin{array}{cccc}
    0 & 1 & 0 & 0 \\
    1 & 0 & 0 & 0 \\
    0 & 0 & 1 & 0 \\
    0 & 0 & 0 & 1  
\end{array}\right] \left[\begin{array}{c}
    \alpha_1 \\
    \alpha_2 \\
    \alpha_3 \\
    \alpha_4
\end{array}\right] \\
= \left[\begin{array}{cccc}
    1 & 0 & -1 & -0.5 \\
    -0.5 & -1 & 0 & 0 \\
    -0.5 & -1 & 0 & 1 \\
    0 & 0 & -1 & -0.5
\end{array}\right] \left[\begin{array}{c}
    \alpha_1 \\
    \alpha_2 \\
    \alpha_3 \\
    \alpha_4
\end{array}\right] \equiv \mathbf{V}_{diff} \mathbf{\alpha}

最適化手法についても前述した例で同様に考えてみる。まず、この問題設定にあわせて$\mathbf{x}$を書き下さす。

(xxiii)

\mathbf{x} = \left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    t^+_1 \\
    t^+_2 \\
    t^+_3 \\
    t^+_4 \\
    t^-_1 \\
    t^-_2 \\
    t^-_3 \\
    t^-_4 \\
    \alpha^+_1 \\
    \alpha^+_2 \\
    \alpha^+_3 \\
    \alpha^+_4 \\
    \alpha^-_1 \\
    \alpha^-_2 \\
    \alpha^-_3 \\
    \alpha^-_4
\end{array}\right]

式(xix)に式(xxii)でもとめたパラメータを当てはめてゆく。

(xxiv)a

\underset{\mathbf{x}}{\text{minimize}}\quad \left[\begin{array}{c}
     -1\\
     -1 \\
     -1 \\
     -1 \\
     0\\
     0\\
     0 \\
     0\\
     0\\
     0\\
     0 \\
     0 \\
     0\\
     0\\
     0\\
     0 \\
     0\\
     0\\
     0 \\
     0
\end{array}\right]^T\left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    t^+_1 \\
    t^+_2 \\
    t^+_3 \\
    t^+_4 \\
    t^-_1 \\
    t^-_2 \\
    t^-_3 \\
    t^-_4 \\
    \alpha^+_1 \\
    \alpha^+_2 \\
    \alpha^+_3 \\
    \alpha^+_4 \\
    \alpha^-_1 \\
    \alpha^-_2 \\
    \alpha^-_3 \\
    \alpha^-_4
\end{array}\right]

s.t.

(xxiv)b

\left[\begin{array}{cccc}
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0 \\
     -1 & 0 & 0 & 0\\
     0 & -1 & 0 & 0\\
     0 & 0 & -1 & 0 \\
     0 & 0 & 0 & -1 \\
     1 & 0 & 0 & 0\\
     0 & 1 & 0 & 0\\
     0 & 0 & 1 & 0 \\
     0 & 0 & 0 & 1 \\
     1 & -0.5 & -0.5 & 0\\
     0 & -1 & -1 & 0\\
     -1 & 0 & 0 & -1 \\
     -0.5 & 0 & 1 & -0.5 \\
     -1 & 0.5 & 0.5 & 0\\
     0 & 1 & 1 & 0\\
     1 & 0 & 0 & 1 \\
     0.5 & 0 & -1 & 0.5 \\
\end{array}\right]^T\left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    t^+_1 \\
    t^+_2 \\
    t^+_3 \\
    t^+_4 \\
    t^-_1 \\
    t^-_2 \\
    t^-_3 \\
    t^-_4 \\
    \alpha^+_1 \\
    \alpha^+_2 \\
    \alpha^+_3 \\
    \alpha^+_4 \\
    \alpha^-_1 \\
    \alpha^-_2 \\
    \alpha^-_3 \\
    \alpha^-_4
\end{array}\right] = \left[\begin{array}{c}
    0 \\
    0 \\
    0 \\
    0 
\end{array}\right]

(xxiv)c

\left[\begin{array}{cccc}
     1 & 0 & 0 & 0\\
     0 & 1 & 0 & 0\\
     0 & 0 & 1 & 0 \\
     0 & 0 & 0 & 1 \\
     -1 & 0 & 0 & 0\\
     0 & -1 & 0 & 0\\
     0 & 0 & -1 & 0 \\
     0 & 0 & 0 & -1 \\
     \eta & 0 & 0 & 0\\
     0 & \eta & 0 & 0\\
     0 & 0 & \eta & 0 \\
     0 & 0 & 0 & \eta \\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0
\end{array}\right]^T\left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    t^+_1 \\
    t^+_2 \\
    t^+_3 \\
    t^+_4 \\
    t^-_1 \\
    t^-_2 \\
    t^-_3 \\
    t^-_4 \\
    \alpha^+_1 \\
    \alpha^+_2 \\
    \alpha^+_3 \\
    \alpha^+_4 \\
    \alpha^-_1 \\
    \alpha^-_2 \\
    \alpha^-_3 \\
    \alpha^-_4
\end{array}\right] \preceq \left[\begin{array}{c}
    0 \\
    0 \\
    0 \\
    0 
\end{array}\right]

(xxiv)d

\left[\begin{array}{cccc}
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0 \\
     1 & 0 & 0 & 0\\
     0 & 1 & 0 & 0\\
     0 & 0 & 1 & 0 \\
     0 & 0 & 0 & 1 \\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0
\end{array}\right]^T\left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    t^+_1 \\
    t^+_2 \\
    t^+_3 \\
    t^+_4 \\
    t^-_1 \\
    t^-_2 \\
    t^-_3 \\
    t^-_4 \\
    \alpha^+_1 \\
    \alpha^+_2 \\
    \alpha^+_3 \\
    \alpha^+_4 \\
    \alpha^-_1 \\
    \alpha^-_2 \\
    \alpha^-_3 \\
    \alpha^-_4
\end{array}\right] \preceq \left[\begin{array}{c}
    1 \\
    1 \\
    1 \\
    1 
\end{array}\right]

(xxiv)e

\left[\begin{array}{cccc}
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0\\
     0 & 0 & 0 & 0 \\
     0 & 0 & 0 & 0\\
     1 & 0 & 0 & 0\\
     0 & 1 & 0 & 0\\
     0 & 0 & 1 & 0 \\
     0 & 0 & 0 & 1 \\
\end{array}\right]^T\left[\begin{array}{c}
    t_1 \\
    t_2 \\
    t_3 \\
    t_4 \\
    t^+_1 \\
    t^+_2 \\
    t^+_3 \\
    t^+_4 \\
    t^-_1 \\
    t^-_2 \\
    t^-_3 \\
    t^-_4 \\
    \alpha^+_1 \\
    \alpha^+_2 \\
    \alpha^+_3 \\
    \alpha^+_4 \\
    \alpha^-_1 \\
    \alpha^-_2 \\
    \alpha^-_3 \\
    \alpha^-_4
\end{array}\right] \preceq \left[\begin{array}{c}
    1 \\
    1 \\
    1 \\
    1 
\end{array}\right]

導出した行列を実際に線形計画法にいれてみよう。

import numpy as np
from scipy.optimize import linprog

c = np.array(
    [-1, -1, -1, -1,
      0,  0,  0,  0,
      0,  0,  0,  0,
      0,  0,  0,  0,
      0,  0,  0,  0]
)

eta = 2.0

# (P_pi - P_a)(I - gamma * P_pi)^-1 * Phi
V_diff = np.array([
    [ 1.0,  0.0, -1.0, -0.5],
    [-0.5, -1.0,  0.0,  0.0],
    [-0.5, -1.0,  0.0,  1.0],
    [ 0.0,  0.0, -1.0, -0.5],
])

# eq. (xxvi)-b
A_eq = np.hstack(
        [np.zeros((4, 4)), -np.eye(4), np.eye(4), V_diff, -V_diff],
).astype(np.float)

b_eq = np.zeros(4)

A_ub = np.vstack([
# eq. (xxvi)c
    np.hstack(
        [np.eye(4), -np.eye(4), eta * np.eye(4), np.zeros((4, 8))]),
# eq. (xxvi)d
    np.hstack(
        [np.zeros((4, 12)), np.eye(4), np.zeros((4, 4))]),
# eq. (xxvi)e
    np.hstack(
        [np.zeros((4, 12)), np.zeros((4, 4)), np.eye(4)]),
]).astype(np.float)

b_ub = np.concatenate([
# eq. (xxvi)c
    np.zeros(4),
# eq. (xxvi)d
    np.ones(4),
# eq. (xxvi)e
    np.ones(4),
])

linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq)
結果
     fun: -4.0
 message: 'Optimization terminated successfully.'
     nit: 10
   slack: array([ 0.,  0.,  0.,  0.,  1.,  1.,  1.,  1.,  1.,  0.,  0.,  1.])
  status: 0
 success: True
       x: array([ 1.,  1.,  1.,  1.,  1.,  1.,  1.,  1.,  0.,  0.,  0.,  0.,  0.,
        0.,  0.,  0.,  0.,  1.,  1.,  0.])

上記 x の値を整理すると結果は $\alpha_1 = 0$ 、 $\alpha_2 = -1$ 、 $\alpha_3 = -1$ 、 $\alpha_4 = 0$ となる。$\alpha_1 = 1$ 、 $\alpha_2 = 0$ 、 $\alpha_3 = 0$ 、 $\alpha_4 = 1$ のような結果を想定していたが、期待値でスケーリングされているだけで意味合い的には同じである。

小括

連続的な空間において、最適な方策が与えらた時に、報酬関数を推定する方法について説明した。しかし、実際には最適な方策が得られることは現実的な問題ではまずありえない。

その3では、その2で説明した離散空間における逆強化学習を最適な方策ではなく、熟練者の行動サンプルが与えられた場合に拡張する（第5章）

参考文献

  1. 離散有限空間において最適な方策が与えられたときのIRLとの比較という形で説明したが、正確には論文内式(10)の $\mathbb{E}_{s' \sim P_{s\pi^*(s_i)}}[V^\pi(s')] \geq \mathbb{E}_{s' \sim P_{sa}}[V^\pi(s')]$ によって導かれる。 ↩

  2. この特徴量は、とにかくある閾値を超えさえすれば良いという今回の問題設定ぐらいでしか使えないであろう。 ↩

  3. 連続空間におけるIRLでは、行列$\mathbf{P}$がうまく埋まるようにサンプルすると良いと思われるが、論文内で説明されていない。 ↩

10
16
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
10
16