目標:$\boldsymbol{R} \in SO(3)$や$\boldsymbol{T} = [\boldsymbol{R} \mid \boldsymbol{t}] \in SE(3)$ について群の定義を踏まえた上で理解しよう
1. 回転表現
1.1 よく使われる回転表現について
ある点 $\boldsymbol{p} \in \mathbb{R}^3$ の3次元回転を考えるとき、以下のような方法が挙げられる。
✅ 回転行列
$\boldsymbol{p}' = \boldsymbol{R}\boldsymbol{p}$
- 回転行列$\boldsymbol{R}$を左から掛け合わせることで回転を表現する方法である
- 9つのパラメータが必要で冗長である
✅ オイラー角
$\boldsymbol{p}' = \boldsymbol{R}_z(\gamma)\boldsymbol{R}_y(\beta)\boldsymbol{R}_x(\alpha)\boldsymbol{p}$
- 3つの角度($\alpha, \beta, \gamma$)の組で回転を表現する
- ジンバルロックという特異点の問題がある
✅ クオータニオン
$\boldsymbol{P}' = \boldsymbol{q}\boldsymbol{P}\boldsymbol{q}^{-1}$
- 4つの要素($w, x, y, z$)で回転を表現する。点$\boldsymbol{p}$を純クオータニオン$\boldsymbol{P} = 0 + p_x \boldsymbol{i} + p_y \boldsymbol{j} + p_z \boldsymbol{k}$に変換し、単位クオータニオン$\boldsymbol{q}$で挟み込むように計算する
- 直感的に理解しにくい
✅ ロドリゲスの回転公式
$\boldsymbol{p}' = \boldsymbol{p}\cos\theta+(\boldsymbol{k} \times \boldsymbol{p})\sin\theta+\boldsymbol{k}(\boldsymbol{k} \cdot \boldsymbol{p})(1-\cos\theta)$
- 回転軸ベクトル$\boldsymbol{k}$と回転角$\theta$から直接、回転後のベクトルを計算する公式である
- 連続した回転の合成が複雑である
📖 参照資料
ゲームプログラマのための数学の歩き方 -クォータニオンとリー群編
クォータニオン (Quaternion) を総整理! ~ 三次元物体の回転と姿勢を鮮やかに扱う ~
1.2 リー群に付随するリー代数を用いると
例えば、変換行列$\boldsymbol{T} $は特殊ユークリッド群$SE(3)$というリー群に属しており、それに付随するリー代数を用いることにより、いくつかのメリットが得られる。
-
パラメータが最小限
パラメータが6つで済む。微小変位で更新していく際に、回転動作に無駄が生じない -
Jacobianがシンプルになる
リー代数を用いて導出したJacobianはソースコード上でたった数行で書ける -
ジンバルロックの回避
オイラー角で発生する特異点問題を回避できる
📖 *参照資料
ロボット技術者向け リー群の速習(1) リー群・リー代数を使った3次元回転表現
2. 群とは
群とは、ある性質を満たす集合と演算の組のことである。
2.1 二項演算の定義
集合 $G$ の元 $\boldsymbol{a}, \boldsymbol{b} \in G$ に対して、$\boldsymbol{a} \cdot \boldsymbol{b} \in G$ となるような演算 $\cdot$ を $G$ 上の二項演算という。
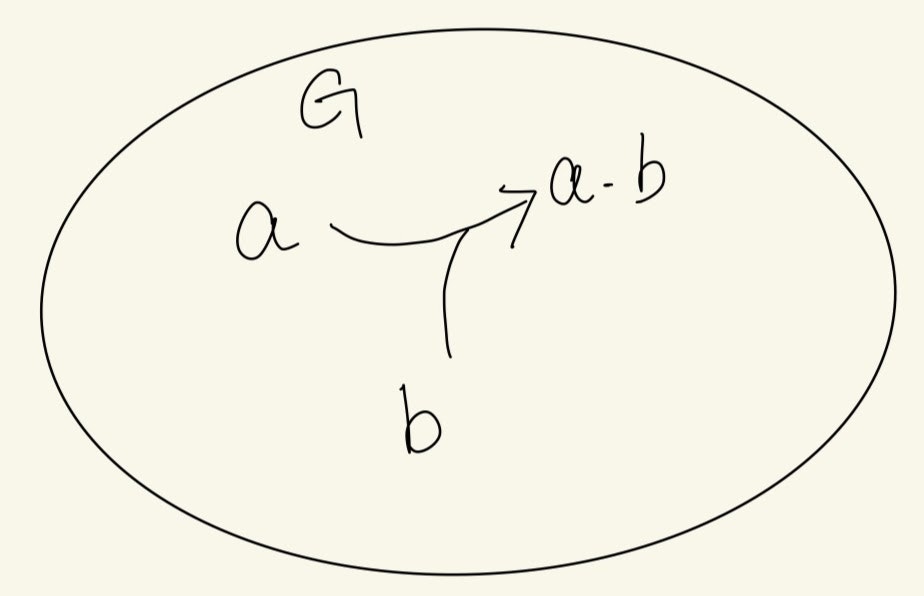
2.2 群の定義
群とは、空でない集合 $G$ とその上の二項演算 $\cdot$ の組 $(G, \cdot)$ であり、以下の3つの性質を満たすものである。
- 結合法則
任意の $\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c} \in G$ に対して、$(\boldsymbol{a} \cdot \boldsymbol{b}) \cdot \boldsymbol{c} = \boldsymbol{a} \cdot (\boldsymbol{b} \cdot \boldsymbol{c})$- 単位元の存在
ある元 $\boldsymbol{e} \in G$ が存在して、任意の $\boldsymbol{a} \in G$ に対して $\boldsymbol{a} \cdot \boldsymbol{e} = \boldsymbol{e} \cdot \boldsymbol{a} = \boldsymbol{a}$- 逆元の存在
任意の $\boldsymbol{a} \in G$ に対して、$\boldsymbol{a} \cdot \boldsymbol{b} = \boldsymbol{b} \cdot \boldsymbol{a} = \boldsymbol{e}$ を満たす $\boldsymbol{b} \in G$ が存在する
群の例
| 群 | 集合 | 演算 | 結合法則 | 単位元 | 逆元 |
|---|---|---|---|---|---|
| $(\boldsymbol{Z}, +)$ | 整数全体の集合 $\boldsymbol{Z}$ | 加法 $+$ | $(\boldsymbol{a} + \boldsymbol{b}) + \boldsymbol{c} = \boldsymbol{a} + (\boldsymbol{b} + \boldsymbol{c})$ | $\boldsymbol{0}$ | $-\boldsymbol{a}$ |
| 一般線形群 $GL(n, \mathbb{R})$ | $n \times n$ の正則行列の集合 | 行列の積 | $(\boldsymbol{A}\boldsymbol{B})\boldsymbol{C} = \boldsymbol{A}(\boldsymbol{B}\boldsymbol{C})$ | 単位行列 $\boldsymbol{I}$ | 逆行列 $\boldsymbol{A}^{-1}$ |
💡 補足
$(\boldsymbol{Z}, +)$のように、群の性質に加えて、可換法則(交換法則)が成り立つ群を可換群と呼ぶ。$GL(n, \mathbb{R})$は可換法則が成り立たないので、非可換群である。
📖 参照資料
2.3 部分群の定義
群 $(G, \cdot)$ の部分集合 $H$ が$G$ の演算 $\cdot$ で群となるとき、$H$ を部分群と呼ぶ。
💡 補足
集合の要素が完全に一致する場合($G$ = $H$)も$H$は部分群である。
📖 部分群の判定方法
数学の景色 部分群の定義と判定方法~例4つと性質~
3. リー群
リー群の扱い方は大きく分けて2つある。
- 線形リー群を中心に扱う(群の定義からつなげやすい)
- 多様体の性質を兼ね備えた群として扱う(リー代数の定義へ繋げやすい)
3.1 線形リー群
3.1.1 線形リー群の定義
一般線形群 $GL(n, \mathbb{R})$ の閉部分群(閉集合かつ部分群)を線形リー群という。
📖 閉集合について
努力のガリレオ 開集合と閉集合をわかりやすく解説しました
🤔 線形リー群の線形とは?
調べてもはっきりしませんでしたが、線形変換の線形からくるものだと予想。
いきなり線形リー群が出てきたが、リー群の代表例が線形リー群であり、実際のところはほとんど線形リー群と考えれば良い。
📖 参照資料
- 連続群論入門
- 線型リー群
- ゆるふわリー群論入門(2)線形リー群
3.1.2 線形リー群の例
線形リー群にはいくつか種類がある。
| 名称 | 条件 |
|---|---|
| 一般線形群 General Linear Group |
$GL(n, \mathbb{R}) = \lbrace \boldsymbol{A} \in \mathbb{R}^{n \times n} \mid \det(\boldsymbol{A}) \neq 0 \rbrace$ $GL(n, \mathbb{C}) = \lbrace \boldsymbol{A} \in \mathbb{C}^{n \times n} \mid \det(\boldsymbol{A}) \neq 0 \rbrace$ |
| 特殊線形群 Special Linear Group |
$SL(n, \mathbb{R}) = \lbrace \boldsymbol{A} \in GL(n, \mathbb{R}) \mid \det(\boldsymbol{A}) = 1 \rbrace$ $SL(n, \mathbb{C}) = \lbrace \boldsymbol{A} \in GL(n, \mathbb{C}) \mid \det(\boldsymbol{A}) = 1 \rbrace$ |
| 直交群 Orthogonal Group |
$O(n) = \lbrace \boldsymbol{A} \in GL(n, \mathbb{R}) \mid \boldsymbol{A}^T \boldsymbol{A} = \boldsymbol{I} \rbrace$ |
| 特殊直交群 Special Orthogonal Group |
$SO(n) = \lbrace \boldsymbol{A} \in GL(n, \mathbb{R}) \mid \boldsymbol{A}^T \boldsymbol{A} = \boldsymbol{I}, \det(\boldsymbol{A}) = 1 \rbrace$ |
| 特殊ユークリッド群 Special Euclidean Group |
$SE(n) = \lbrace \boldsymbol{T} = [ \boldsymbol{R} \mid \boldsymbol{t} ] \mid \boldsymbol{R} \in SO(n), \boldsymbol{t} \in \mathbb{R}^n \rbrace$ |
💡 補足
- 特殊線形群と直交群の共通部分が特殊直交群
- 3次元の回転行列は$SO(3)$に属する
- 3次元の剛体変換は$SE(3)$に属する
📖 参照資料
3.2 多様体である群がリー群
リー群とは
リー群は、多様体としての性質を兼ね備える群のことである。
🤔 多様体とは?
多様体とはどこでも好きなところに局所座標系が描けるような空間である
📖 参照資料
- 多様体の基礎
- ゆるふわリー群論入門(3)多様体
- 多様体の基礎のキソ
- 付録 微分可能多様体
次回、リー代数を定義する上で、多様体の話が起点となる。
まとめ
- リー代数を用いると、回転成分に関しては自由度と同じ3つのパラメータだけで済むなどのメリットがある
- 群とは集合と演算のペアである
- 回転行列$\boldsymbol{R}$は特殊直交群、同次変換行列$\boldsymbol{T}$は特殊ユークリッド群の元である