※社内の勉強会で使ったものを読みやすく再構成しました
はじめに
ロボティクス工学だけではなく、あらゆる工学分野で3次元回転を表現する必要がある。有名な回転表現方法として、回転行列(rotation matrix)、オイラー角(euler angles)、クォータニオン(quaternion)、軸角(Axis-angle)などが挙げられる。しかし、近年、リー群(Lie Group)による回転表現をロボティクスの研究に導入して、非常に有効であることが示された。リー群による回転表現を理解しないと、最新のロボティクス論文(特にSLAM)が読めないと言っても過言ではない。
しかし、大学時代に群論(Group theory)を勉強したことがある人は少なく、いきなりリー群を勉強しても、どこから勉強すれば良いかがわからないだろう。この文章は、従来の回転表現から、リー群・リー代数による回転表現を導入し、なぜリー群・リー代数が必要か、工学的にどのように応用しているかを説明する。この文章を読むことによって、短い時間でSLAM研究に必要な回転、リー群とリー代数の知識をキャッチアップできたら嬉しい。
$$
\newcommand{\skew}[1]{[{#1}]_{\times}} %skew matrix
\newcommand{\so}[1]{ \mathfrak{so}{(#1)} } %lie algebra so3
\newcommand{\norm}[1]{|{#1}|} %norm
$$
回転行列
最もシンプルな3次元回転表現は3X3の回転行列である。行列の掛け算だけで、回転を適用できるため、非常に高速的に計算ができる。しかし、3X3の回転行列は9個の独立変数があり、非常に冗長な表現である。もし、最適化(Gauss–Newton methodなど)により回転を推定する場合に、直接に3X3の行列を使ったとしたら、結果として、回転行列ではない行列が得られるだろう。
オイラー角
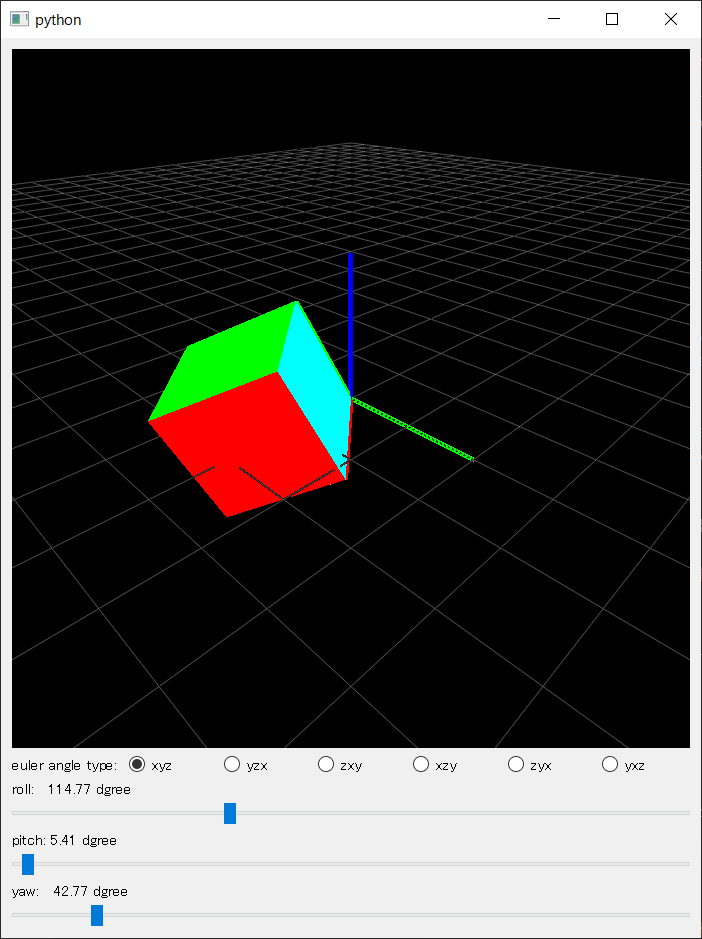
オイラー角はレオンハルト・オイラーにより考案され、各座標軸まわりの3つの回転を順番的に組み合わせた回転表現である。
各座標軸まわりの3つの回転は以下のように定義する。
- $\alpha$: Roll, x軸まわりの角度
- $\beta$: Pitch, y軸まわりの角度
- $\gamma$: Yaw, z軸まわりの角度
イメージ:

それぞれ軸の回転行列は以下:
x軸まわりの回転行列
$$
R_x(\alpha) =
\left[\begin{matrix} 1 & 0 & 0 \\
0 & \cos\alpha & -\sin\alpha \\
0 & \sin\alpha & \cos\alpha
\end{matrix}\right]
\tag{1}
$$
y軸まわりの回転行列
$$
R_y(\beta) = \left[\begin{matrix} \cos\beta & 0 & \sin\beta \\
0 & 1 & 0 \\
-\sin\beta & 0 & \cos\beta \end{matrix}
\right]
\tag{2}
$$
z軸まわりの回転行列
$$
R_z(\gamma) =
\left[\begin{matrix} \cos\gamma & -\sin\gamma & 0 \\
\sin\gamma & \cos\gamma & 0 \\
0 & 0 & 1
\end{matrix}\right]
\tag{3}
$$
以上、三つの回転行列を掛け算すると、任意の三次元回転が表現できるが、行列の掛け算は可換則を満たさないため、x,y,z回転の順序が変わると、最終的に異なる回転行列が生成される。
オイラー角は全部で12通りの表現法がある。
| xyz | xzy | yxz | yzx | zxy | zyx | xyx | xzx | yxy | yzy | zxz | zyz |
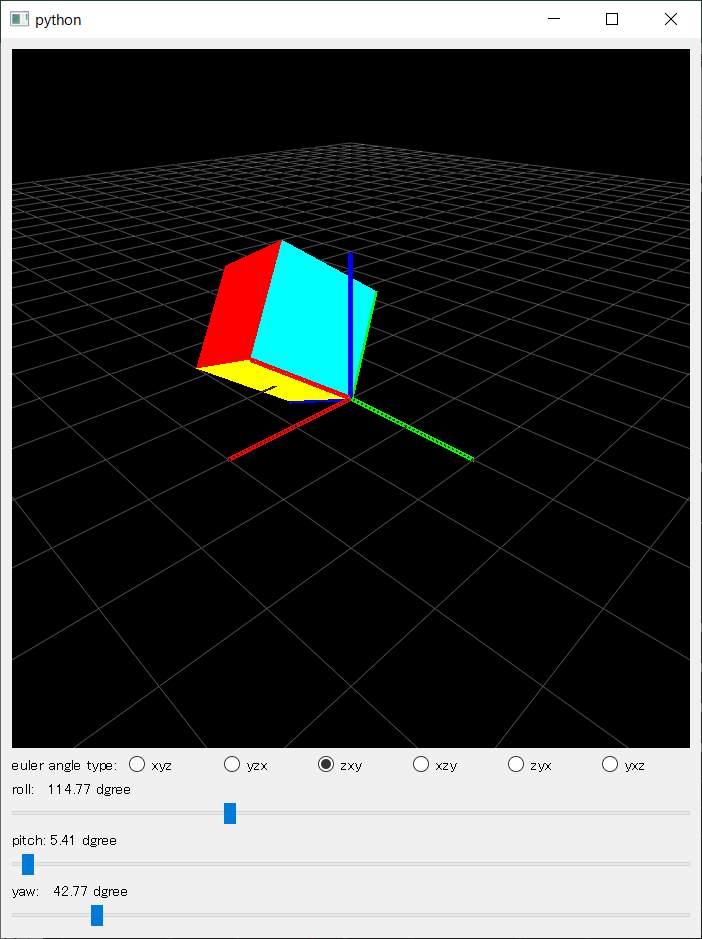
以下にXYZとZXYオイラー角の計算を示す。明らかに最終な回転行列は全く異なる。そのため、オイラー角を使うときには、回転の順番を決めることが非常に重要である。
XYZオイラー角
以下$\sin\theta$、$\cos\theta$をそれぞれ$s_\theta$、$c_\theta$と略す。
$$
\begin{aligned} R_{xyz}(\alpha, \beta, \gamma)
&=
R_z (\gamma) R_y (\beta) R_x (\alpha) \\
&=
\left[\begin{matrix} c_\gamma & -s_\gamma & 0 \\
s_\gamma & c_\gamma & 0 \\
0 & 0 & 1
\end{matrix}\right]
\left[\begin{matrix} c_\beta & 0 & s_\beta \\
0 & 1 & 0 \\
-s_\beta & 0 & c_\beta
\end{matrix}\right]
\left[\begin{matrix} 1 & 0 & 0 \\
0 & c_\alpha & -s_\alpha \\
0 & s_\alpha & c_\alpha
\end{matrix}\right] \\
&=
\left[\begin{matrix} c_{\gamma} c_{\beta} & c_{\gamma} s_{\beta} s_{\alpha} - c_{\alpha} s_{\gamma} & s_{\gamma} s_{\alpha} + c_{\gamma} c_{\alpha} s_{\beta} \\
c_{\beta} s_{\gamma} & c_{\gamma} c_{\alpha} + s_{\gamma} s_{\beta} s_{\alpha} & c_{\alpha} s_{\gamma} s_{\beta}- c_{\gamma} s_{\alpha} \\
-s_{\beta} & c_{\beta} s_{\alpha} & c_{\beta} c_{\alpha} \\
\end{matrix}\right]
\end{aligned} \tag{4}
$$
ZXYオイラー角
$$
\begin{aligned} R_{zxy}(\alpha, \beta, \gamma)
&=
R_y (\beta) R_x (\alpha) R_z (\gamma) \\
&=
\left[\begin{matrix} c_\beta & 0 & s_\beta \\
0 & 1 & 0 \\
-s_\beta & 0 & c_\beta
\end{matrix}\right]
\left[\begin{matrix} 1 & 0 & 0 \\
0 & c_\alpha & -s_\alpha \\
0 & s_\alpha & c_\alpha
\end{matrix}\right]
\left[\begin{matrix} c_\gamma & -s_\gamma & 0 \\
s_\gamma & c_\gamma & 0 \\
0 & 0 & 1
\end{matrix}\right] \\
&=
\left[\begin{matrix} c_{\beta} c_{\gamma}+s_{\beta} s_{\alpha} s_{\gamma} & c_{\gamma} s_{\beta} s_{\alpha}-c_{\beta} s_{\gamma} & c_{\alpha}s_{\beta} \\
c_{\alpha} s_{\gamma} & c_{\alpha} c_{\gamma} & -s_{\alpha} \\
c_{\beta} s_{\alpha} s_{\gamma}-s_{\beta} c_{\gamma} & s_{\beta} s_{\gamma}+c_{\beta} c_{\gamma} s_{\alpha} & c_{\beta} c_{\alpha}
\end{matrix}\right]
\end{aligned}
\tag{5}
$$
ジンバルロック
オイラー角は頻繁に使われるが、ジンバルロックという問題も有名である。
例えば、XYZオイラー角の場合、pitch=90°のとき、rollとyawは同じ軸を回転することになる。
証明:
$$
\begin{aligned} R_{xyz}(\alpha, \frac{\pi}{2}, \gamma) \
&=
\left[\begin{matrix} c_\gamma & -s_\gamma & 0 \\
s_\gamma & c_\gamma & 0 \\
0 & 0 & 1
\end{matrix}\right]
\left[\begin{matrix} 0 & 0 & 1 \\
0 & 1 & 0 \\
-1 & 0 & 0
\end{matrix}\right]
\left[\begin{matrix} 1 & 0 & 0 \\
0 & c_\alpha & -s_\alpha \\
0 & s_\alpha & c_\alpha
\end{matrix}\right] \\
&=
\left[\begin{matrix}
0 & -c_\alpha s_\gamma + c_\gamma s_\alpha & c_\alpha c_\gamma + s_\gamma s_\alpha \\
0 & c_\alpha c_\gamma + s_\gamma s_\alpha & c_\alpha s_\gamma - c_\gamma s_\alpha \\
-1 & 0 & 0
\end{matrix}\right] \\
&=
\left[\begin{matrix}
0 & s_\theta & c_\theta \\
0 & c_\theta & -s_\theta \\
-1 & 0 & 0
\end{matrix}\right] \\
\end{aligned} \tag{6}
$$
式(6)から、pitch=90°のとき、$R_{xyz}$はZ軸回りの回転となり、回転角度は$\theta$($\theta = \alpha - \gamma$)となる。
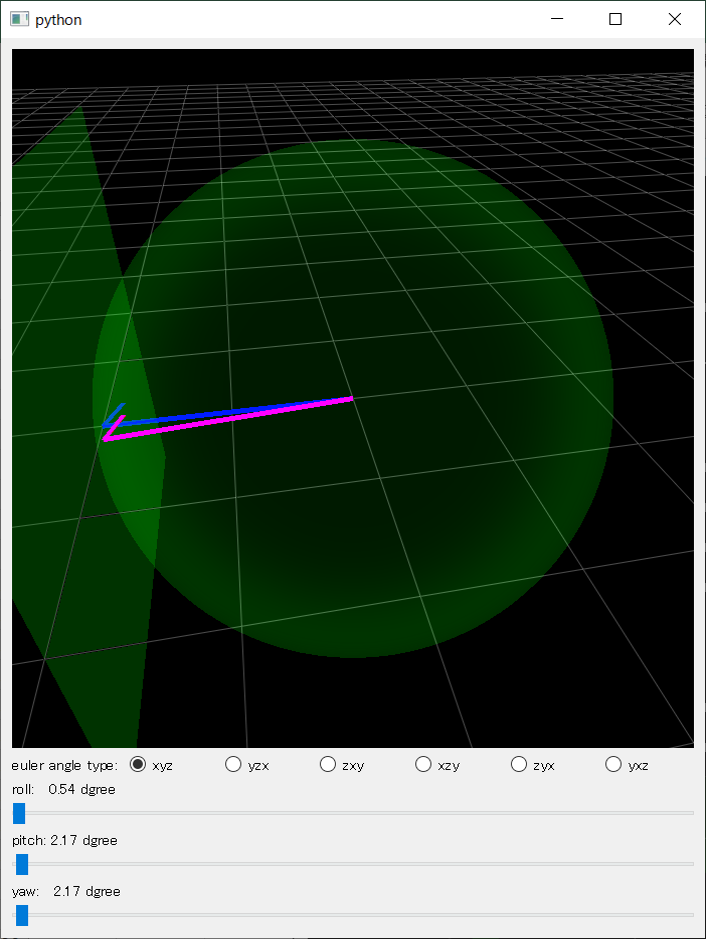
ジンバルロックのイメージ:rollとyawを変えたとき、同じZ軸回りに回転する。

ジンバルロック問題が存在するために、オイラー角は数学的に非連続的な回転表現である。また、非可換、非線形(sin,cosがある)という性質があるため、多くの数学的問題で扱いにくいものとなる。
微小回転
オイラー角の問題を解決するため、先に微小な回転を考えよう。
三角代数的に角度が十分小さければ、以下の式が成り立つ。
- $\cos(a) \approx 1$
- $\sin(a) \approx a$
- $\sin(a) \sin(b) \approx 0$
上記式を(4)、(5)に代入すると、全く同じ結果が得られる。
つまり、微小な回転は普通のオイラー角と異なり、回転の順番と関係なく、数学的に可換である。
$$
\begin{aligned}
R_{xyz} \approx R_{zxy} &\approx
\left[\begin{matrix} 1 & - \gamma & \beta \\
\gamma & 1 & - \alpha \\
-\beta & \alpha & 1 \\
\end{matrix}\right] \\
&= I +
\left[\begin{matrix} 0 & - \gamma & \beta \\
\gamma & 0 & - \alpha \\
-\beta & \alpha & 0 \\
\end{matrix}\right] \\
&= I + \skew{\omega}
\end{aligned}
\qquad if \quad \alpha, \beta, \gamma \ll 1
\tag{7}
$$
$\skew{\omega}$ は $\alpha$, $\beta$ と $\gamma$から構成された交代行列(skew-symmetric matrix)であり、$\omega$は3次元空間に属する($\omega \in \mathbb{R}^3$)。
また、式(7)の結果には、$\sin$、$\cos$などが含まれず、完全に線形であるため、非常に計算しやすいものとなる。
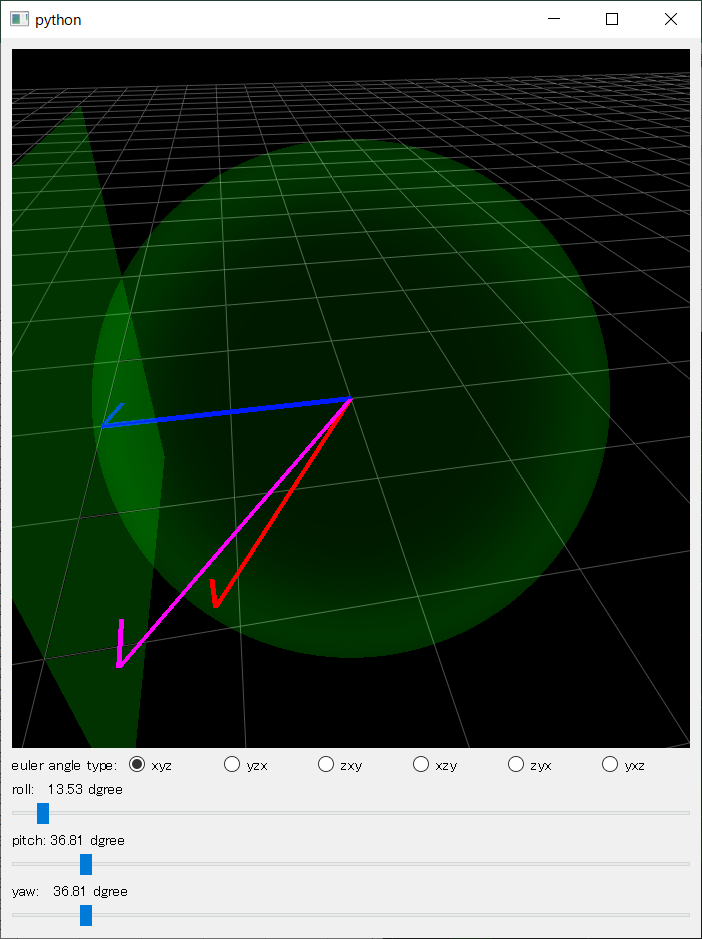
以下の図は微小回転(紫)と回転行列(赤)が同じベクトル(青)を回転させる結果を示す。回転行列の結果はベクトルを球面上で動かし、一方、微小回転はこの球面の接平面(Tangent space)に動かす。回転が小さいとき、球面も平面に近似できるため、微小回転の精度も十分高い。
回転の合成
これで小さな回転を可換かつ線形な表現で表すことができたが。残る問題は、より大きな回転をどのように表現するか?
とてもシンプルな考えるとして、大きな回転の3次元ベクトル$\omega$をn個(無限大に近い)に小さく分割し、掛け算で合成すれば良い。
$$
R(\omega) =
\underbrace{(I+\frac{\skew{\omega}}{n}) \times ... (I+\frac{\skew{\omega}}{n})}_\text{n factors}
=(I+\frac{\skew{\omega}}{n})^n
\tag{8}
$$
数学素養がある人なら、この式に見覚えがあるのではないだろうか。実数の場合、この無限乗積は非常に有名な指数関数の定義である。
同様に、上式を行列の指数関数として定義できる(式(9))。
$$
R(\omega)
=\lim_{n \to \infty}(I+\frac{\skew{\omega}}{n})^n = e^{\skew{\omega}}
\tag{9}
$$
さらに、nは無限大の時、二項定理(binomial theorem)より式(9)を展開する場合、行列の指数関数を式(10)のように変形できる。
こうして、我々は指数写像(10)を用いて、3次元ベクトルを回転行列に変換することができた。
$$
R(\omega)
= e^{\skew{\omega}}
=\sum_{k=0}^\infty \frac{\skew{\omega}^k}{k!}
\tag{10}
$$
ここまで、リー群という言葉を一回も使ってないが、実は、上記の計算で既にリー群の知識を議論した。3次元回転空間 $R$ は、特殊直交群 $SO(3)$ と呼ばれる。3次元ベクトル $\omega$の空間は、リー代数 $\so3$ と呼ばれ、指数写像によって $SO(3)$ に変換することができる。
群
ここから群(Group)の基本を簡単に紹介する。以下4つの公理を満たす集合は群である。
- 閉集合:
if $a_1, a_2 \in G$, then $a_1 \cdot a_2 \in G$ - 結合則:
if $a_1, a_2, a_3 \in G$, then $(a_1 \cdot a_2) \cdot a_3 = a_1 \cdot ( a_2 \cdot a_3)$ - 単位元:
For every $a \in G$, there exists a $a_0 \in G$, such that $a_0 \cdot a = a \cdot a_0 = a$ - 逆元:
For every $a \in G$, there exists a $a^{-1} \in G$, such that $a \cdot a^{-1} = a_0$
例えば、3次元回転も、ルービックキューブを回すことも群であり、群の公理がすべて満たされていることを簡単に検証することができる。

リー群
リー群は連続的な群であり、この連続的という意味は無限に微分可能(滑らか)である。
従って、ルービックキューブ群は群であるが、リー群ではない。3次元回転空間は、群であると同時にリー群である。
リー群は以下の利点があるため、最近のSLAM研究では、リー群やリー代数を用いることが多い。
- リー代数は3つの値で回転を表すことができる。式(10)
- リー群・リー代数は微分可能である。
- リー群・リー代数にはジンバルロック問題がない。
- 回転が小さい場合に、容易に線形化される。式(7)。
3次元の特殊直交群 SO(3)
SO(3)と$\so3$の指数写像と対数写像を使って、お互いに変換することができる。工学的な応用するとき、指数写像と対数写像の計算方法はとても重要であるため、以下はその計算を導出してみる。
指数写像(Exponential map)
(8)や(9)を使って、$\so3$を$SO(3)$に変換できるが、計算が煩雑であるため(有限項で近似)、以下のように計算を簡略化する。
$\omega = \theta r$ を定義する。
- $r$ : $\omega$の単位ベクトル, $r =\dfrac{\omega}{\norm{\omega}}$
- $\theta$ : $\omega$のノルム, $\theta = \norm{\omega}$
$$
\begin{aligned}
\exp ( \skew{\omega} )
&= \exp ( \theta \skew{r} ) \\
&= \sum\limits_{k = 0}^\infty
\frac{1}{k!} (\theta \skew{r} )^k \\
&= I + \theta \skew{r} +
\frac{1}{2!} \theta^2 \skew{r}^2 +
\frac{1}{3!} \theta^3 \skew{r}^3 +
\frac{1}{4!} \theta^4 \skew{r}^4 + ... \\
&= r^T r -
\skew{r}^2 + \theta \skew{r} +
\frac{1}{2!} \theta^2 \skew{r}^2 +
\frac{1}{3!} \theta^3 \skew{r}^3 +
\frac{1}{4!} \theta^4 \skew{r}^4 + ... \\
&= r^T r - (\skew{r}^2 -
\frac{1}{2!} \theta^2 \skew{r}^2 -
\frac{1}{4!} \theta^4 \skew{r}^4 - ...) + (\theta \skew{r} +\frac{1}{3!} \theta^3 \skew{r}^3 + ...) \\
&= r^T r - (1 -
\frac{1}{2!} \theta^2 +
\frac{1}{4!} \theta^4 - ...)\skew{r}^2 + (\theta -\frac{1}{3!} \theta^3 + ...)\skew{r} \\
&= r^T r - \cos\theta \skew{r}^2 + \sin\theta\skew{r} \\
&= \skew{r}^2 + I - \cos\theta \skew{r}^2 + \sin\theta\skew{r} \\
&= I + (1- \cos\theta) \skew{r}^2 + \sin\theta\skew{r}
\end{aligned}
\tag{11}
$$
(11)の計算では、交代行列の2つの性質が使われている。
$r$は単位ベクトルのとき:
- $\skew{r}\skew{r}\skew{r} = -\skew{r}$
- $r^Tr = \skew{r}^2 + I$
(11)式は、Rodrigues' Formulaとして知られ、$\so3$から$SO(3)$への指数写像の高速&高精度な計算方法である。
対数写像 (Logarithm map)
指数写像と逆に、対数写像は指数写像の逆計算であり、リー代数をリー群に対応させることができる。
式(11)は、行列として書くことができる。
$$
\begin{aligned}
R(\theta, r)
&= I + (1- \cos\theta)
\left[\begin{matrix}
r_1^2 -1 & r_1 r_2 & r_1 r_3 \\
r_1 r_2 & r_2^2-1 & r_2 r_3 \\
r_1 r_3 & r_2 r_3 & r_3^2-1 \\
\end{matrix}\right] +
\sin\theta
\left[\begin{matrix}
0 & -r_3 & r_2 \\
r_3 & 0 & -r_1 \\
-r_2 & r_1 & 0 \\
\end{matrix}\right] \\
&= \left[\begin{matrix}
r_1^2 (1-c_\theta) + c_\theta & r_1 r_2 (1-c_\theta) - r_3 s_\theta & r_1 r_3 (1-c_\theta) + r_2 s_\theta\\
r_1 r_2 (1-c_\theta) +r_3 s_\theta & r_2^2 (1-c_\theta) + c_\theta & r_2 r_3 (1-c_\theta) - r_1 s_\theta\\
r_1 r_3 (1-c_\theta) -r_2 s_\theta & r_2 r_3 (1-c_\theta) + r_1 s_\theta & r_3^2 (1-c_\theta) + c_\theta
\end{matrix}\right]
\end{aligned}
\tag{12}
$$
(12)から:
$$
\theta = \arccos( \frac{1}{2}(R_{11} + R_{22} + R_{33} -1)) \
= \arccos( \frac{1}{2}(tr(r) -1))
\tag{13}
$$
$$
r = \frac{[ R_{32} - R_{23}, R_{13} - R_{31}, R_{21} - R_{12}]}{2 \sin \theta}
\tag{14}
$$
(13) (14)より、対数写像は以下のように計算することができる。
$$
\log(R)^{\vee} = \omega= \theta r = \frac{\theta[ R_{32} - R_{23}, R_{13} - R_{31}, R_{21} - R_{12}]}{2 \sin \theta}
\tag{15}
$$
まとめ
今回は回転行列・オイラー角の性質と欠点を解説し、その欠点を補うため、リー群$SO(3)$とリー代数$\so3$を導入した。$\so3$の指数写像を使って、$SO(3)$へ変換することができる。この変換はとても美しい行列の指数関数である。
また、$SO(3)$に対数写像を用いることで、3次元回転($\in SO(3)$)は3次元空間上のベクトル($\in \so3$)と同等にできる。そのため、パラメータが少ない$\so3$を使えば、回転行列・オイラー角の欠点を回避しながら、回転の最適化を美しい形で行える。
$SO(3)$と$\so3$を工学的に応用するとき、指数と対数写像の計算方法はとても重要であるため、今回は指数と対数写像の計算方法を導出した。式(11)(15)を参考にすれば、容易に実装できるだろう。
リー群・リー代数を導入する最終の目的は、回転の最適化を行うことであるため、次回は、リー群とリー代数最適化について詳細に解説する。
また、今回の内容も含め、数学とロボティクスに関する面白いテーマを以下のgithubに整理しているので、興味があれば見てください。