はじめに
以前、OpenVINO の Person-reidentification(人再認識)モデルを使って人を追跡するを作りましたが、単純にコサイン類似度とユークリッド距離でもって同一性を判定するだけでは、十分ではありませんでした。
GitHub では、コメントをくださる方がいて
- 「なぜ DeepSORT を使わないの?」
- 「Oxford Town Centre VideoでランダムにIDが割り当てられてしまう」
という問題を教えてくれました。
この記事は、DeepSORT のアルゴリズムを参考に、実装できたこと、できなかったこと、試行錯誤したことの 備忘録 です。「人物追跡をやってみよう」 という方の 役に立てば幸いです。
(注意):実装は DeepSORT とは異なります。
DeepSORT のアルゴリズムについては以下がとても参考になります。
できたもの
GitHub
YouTube
注: 画像が Youtubeのリンクになっています(音は出ません)
Oxford Town Cente1 - (YouTube Link)

Shopping mall2 - (YouTube Link)
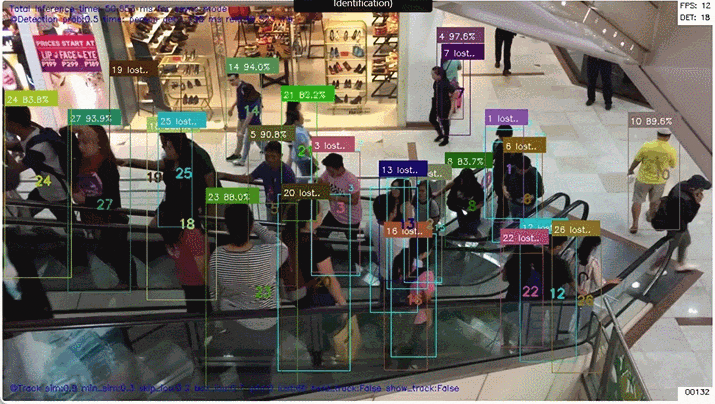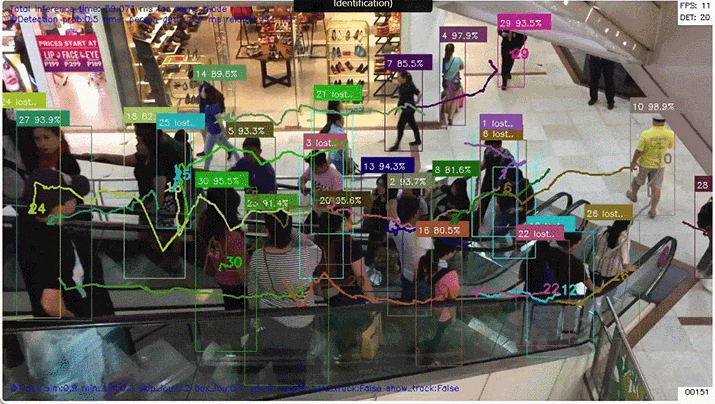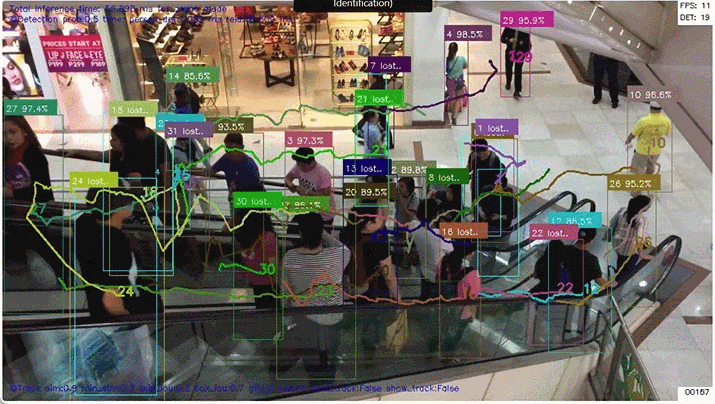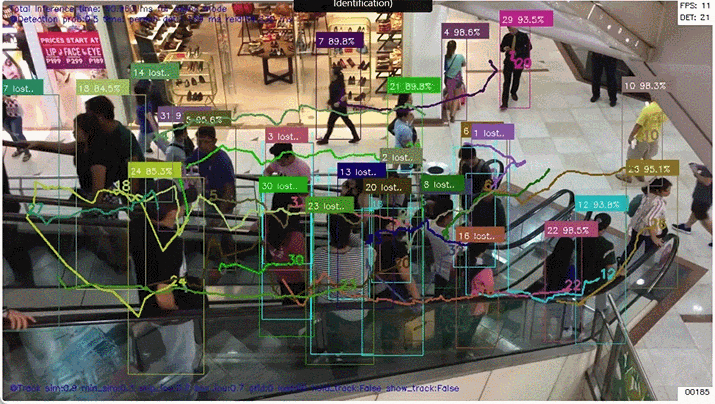
人の再認識
人間には簡単な「再認識 (person_reidentification) 」ですが、コンピュータで「人の特徴を抽出して」、「他の人と比べて」、「同一人物か(似てるか)どうかを評価する」仕組みを作るのは かなり難しいとタスクだと思います。

再認識の仕組み
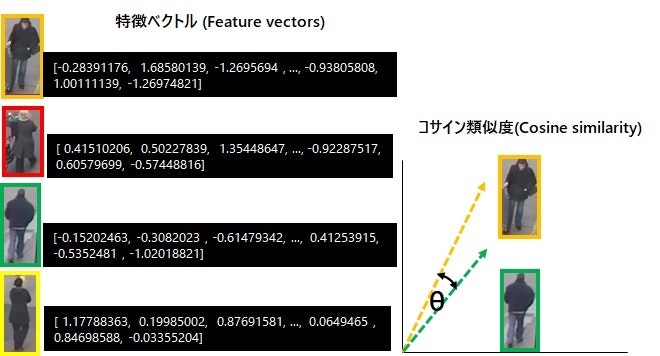
「人の再認識」で人の同一性を判断するには、 特徴ベクトル と コサイン類似度 を使います。
-
特徴ベクトル は、検出した人の見た目を数値化(ベクトル化)したもので、OpenVINO の Person Reidentification モデルを使用して取得できます。Person Reidentification モデルは、検出した人の特徴を 256 次元のベクトル で出力します。
-
コサイン類似度 は ベクトル間のなす角(ラジアン) のコサイン値です。
ベクトルが同じ方向を向いていれば、角度が小さくなりコサイン値が高くなるので 類似度が高いことを示します。
この記事のプログラムでは 以下のモデルを使用しました。
具体的な使い方は以下をご覧ください。
実装ポイント
プログラムを書いてみて 重要と思った点をまとめました。
- 検出(detection): 人として検出されたオブジェクト(未マッチング)
- トラック(track): 再認識して保持したオブジェクト(マッチング済み)
- コサイン距離: 外観情報を考慮(長期のオクルージョンに有効)
- ユークリッド/マハラビノス距離: 位置情報を考慮(短期の予測に有効)
"the Mahalanobis distance provides information about possible object locations based on motion that are particularly useful for short-term predictions. On the other hand, the cosine distance considers appearance information that are particularly useful to recover identities after longterm occlusions, when motion is less discriminative. "
Simple Online and Realtime Tracking with a Deep Association Metricより引用
| No | 実装ポイント | 結果 | メモ |
|---|---|---|---|
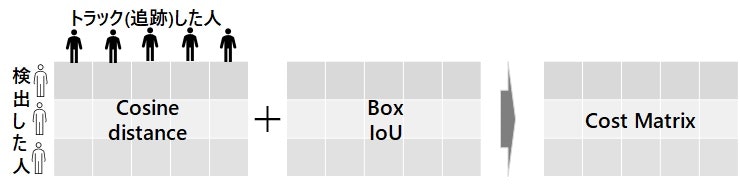
| 1 | コストマトリックス | 〇 | コサイン距離とBBox IoU から 検出 とトラック のコストマトリックスを作成 (DeepSortでは min_cost_matching で IoU を使用) |
| 2 | マハラビノス距離(ゲート処理) | ×(実装できず) | 検出とトラック間のマハラビノス距離より異常値を検出、コストマトリックスから除外する |
| 3 | 割当問題の解決 | 〇 | ハンガリアン法を用いて コストが最小になるように、検出とトラックをマッチングする (マッチング処理 で 一番効果があった) |
| 4 | 線形カルマンフィルタ | 〇 | トラックの位置情報を推定し補正 (カルマンフィルタでの予測は 割当結果を位置情報で評価する際に役立つ) |
| 5 | ユークリッド距離(※) | △(微妙..) | 検出とトラックの距離を 割当結果の評価に使用 (動的閾値の算出に苦慮。最終的に 単純に人物の bboxの横幅以下 を閾値とする方が良い結果に) |
| 6 | マッチングカスケード | ×(対象外) | コサイン距離のマッチング結果 と IoU のマッチング結果を連結。頻繁に見られる直近のオブジェクトを優先する(私の力量では無理でした) |
| 7 | 描画(見た目の工夫) | 〇 | ロストしたトラックについてもカルマンフィルタの状態推定を描画 |
※DeepSORTでは ユークリッド距離は使用していない。
コストマトリックス
ここからは実装の話です。
人物のコサイン類似度(距離)と IOU から コストマトリックスを作成します。Oxford Town Centre (「はじめに」の動画) で 実際のデータで処理の流れを追っていきます。
コサイン距離
OpenVINO の Person Reidentification モデル で取得した コサイン類似度 から コサイン距離 を求めます。
まずコサイン類似度を求めます。
import numpy as np
def cos_similarity(X, Y):
# X: 検出した人の特徴ベクトル
# Y: トラックした人の特徴ベクトル
m = X.shape[0]
Y = Y.T # (m, 256) x (256, n) = (m, n)
return np.dot(X, Y) / (
np.linalg.norm(X.T, axis=0).reshape(m, 1) * np.linalg.norm(Y, axis=0)
)
コサイン類似度の出力例です。 検出した人が 4 、トラックした人が 12 ならが コサイン類似度は 4 x 12 の行列になります。
# cosine matrix 4 x 12
similarities = np.array([
[ 0.376, 0.391, 0.968, 0.135, 0.08 , 0.147, 0.478, 0.222, 0.199, 0.314, -0.072, 0.09 ],
[ 0.315, 0.936, 0.44 , 0.064, -0.062, 0.22 , 0.354, 0.707, 0.28 , 0.014, 0.073, 0.22 ],
[ 0.256, 0.021, 0.163, 0.975, 0.234, 0.266, 0.2 , 0.054, 0.134, 0.452, -0.009, 0.237],
[ 0.079, -0.076, 0.106, 0.241, 0.93 , -0.048, 0.07 , -0.117,-0.043, 0.292, 0.335, -0.043]
])
次に コサイン距離を 1-コサイン類似度 で求めます。コサイン類似度とは逆に、0 に近い(距離が近い)ほど、似ていることになります。
求めた コサイン距離を、cost_matrix とします。
cost_matrix = 1 - similarities
np.round(cost_matrix,2)
# 出力
array([[0.62, 0.61, 0.03, 0.86, 0.92, 0.85, 0.52, 0.78, 0.8 , 0.69, 1.07, 0.91],
[0.68, 0.06, 0.56, 0.94, 1.06, 0.78, 0.65, 0.29, 0.72, 0.99, 0.93, 0.78],
[0.74, 0.98, 0.84, 0.03, 0.77, 0.73, 0.8 , 0.95, 0.87, 0.55, 1.01, 0.76],
[0.92, 1.08, 0.89, 0.76, 0.07, 1.05, 0.93, 1.12, 1.04, 0.71, 0.66, 1.04]])
Box IoU
検出した人とトラックした人の BBox(Bounding Box) の IoU (Intersection over Union) を求め、cost_matrix に加算します。
# 検出した人の bbox (xmin, ymin, xman, ymax)
boxes = [(863,447,927,573),(487,378,547,493),(813,0,851,65),(540,1,587,91)]
# トラックした人の bbox (xmin, ymin, xman, ymax)
track_boxes = np.array(
[[522,81,558,166], [486,375,544,491], [860,441,925,573], [811,0,848,64],
[539,-1,588,91], [882,30,913,108], [494,80,526,165], [407,450,476,569],
[874,395,937,533],[787,2,827,80], [506,15,538,111], [878,50,909,128]]
)
IoU を求めます。複数の BBox を効率的に処理します。
# utils.py
def get_iou(box, boxes):
# Input box : ndarray (1, 4)
# boxes: ndarray (m, 4)
# Output: Iou : ndarray (m,)
ximin = np.maximum(box[0], boxes[:, 0])
yimin = np.maximum(box[1], boxes[:, 1])
ximax = np.minimum(box[2], boxes[:, 2])
yimax = np.minimum(box[3], boxes[:, 3])
inter_width = ximax - ximin
inter_height = yimax - yimin
inter_area = np.maximum(inter_width, 0) * np.maximum(inter_height, 0)
box_ = (box[2] - box[0]) * (box[3] - box[1])
boxes_ = (boxes[:, 2] - boxes[:, 0]) * (boxes[0:, 3] - boxes[0:, 1])
union_area = box_ + boxes_ - inter_area
return inter_area / union_area
人の 動きや重なり度合によって BBox の形にはバラツキがあるので、IoUコストの影響を軽減するため 重み(0.5) を掛けて調整しました。
box_iou_matrix = np.zeros((len(boxes), len(track_boxes)))
for i, box in enumerate(boxes):
box_iou_matrix[i, :] = get_iou(box, track_boxes)
box_iou_matrix = (1 - box_iou_matrix) * 0.5
np.round(box_iou_matrix,2)
# 出力
array([[0.5 , 0.5 , 0.06, 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.31, 0.5 , 0.5 , 0.5 ],
[0.5 , 0.05, 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 ],
[0.5 , 0.5 , 0.5 , 0.07, 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.41, 0.5 , 0.5 ],
[0.49, 0.5 , 0.5 , 0.5 , 0.03, 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 ]])
ここでは特に閾値は設けずに、取得した IoU をコストとして cost_matrix に加算します。
cost_matrix = cost_matrix + box_iou_matrix
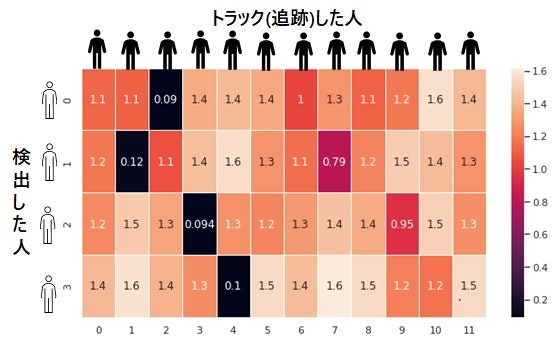
cost_matrix をヒートマップで可視化 すると以下のようになります。
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(10, 5))
sns.heatmap(cost_matrix, annot=True, linewidths=.5)
plt.show()
黒部分がコスト最小であり、例えば、0行目(検出の1人目)は、2列目(トラックの3人目)がコストが最小 で 0.09 です。
同じようにして コストが最小になるように 検出した人に IDを割り当てます。
割当問題(ハンガリアン法)
上で求めた cost_matrix のコストが最小になるように ID 割り当てるには ハンガリアン法を使います。人物のマッチングで一番効果がありました。
Munkres を使いました。3 出力は [row, col] の形式です。
[[0, 2], [1, 1], [2, 3], [3, 4]] が期待値です。 上のヒートマップで コストが低い(黒い)部分が、割り当てとして出力されています。
from munkres import Munkres
m = Munkres()
track_ids = np.array(m.compute(cost_matrix.tolist()))
track_ids.tolist()
# 出力
[[0, 2], [1, 1], [2, 3], [3, 4]]
np.nanargmin() で 最小のインデックスを取ってくれば簡単そうに思えますが、実際は単純ではなく、検出した人に複数のトラックが競合したときに 2番目に低いコストを割り当てるなど、ハンガリアン法は 全体を見て割当問題を最適化してくれます。
線形カルマンフィルタ
「カルマンフィルタの基礎」 の 「第6章 線形カルマンフィルタ」を 参考にしました。
(良く分かっていない部分があるので間違っているかもしれません。filterpy などライブラリを使うのも良いと思います。)
import numpy as np
class KalmanFilter:
def __init__(self, measurement, dt=0.1):
# Noise
R_std = 0.35
Q_std = 0.04
self.R = np.eye(2) * R_std**2
self.Q = np.eye(4) * Q_std**2
# Initiliza State
# 4D state with initial position and initial velocity assigned
self.X = np.array([[measurement[0]], [measurement[1]], [0.0], [0.0]])
#self.Bu = np.zeros((4,4))
#self.U = np.array([[0.0], [0.0], [0.0], [0.0]])
# Initilize Error covariance Matrix
gamma=10
self.P = gamma*np.eye(4)
# State Transition matrix
self.A = np.array(
[
[1.0, 0.0, dt, 0.0],
[0.0, 1.0, 0.0, dt],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0],
]
)
self.B = np.eye(4)
# observation matrix
self.C = np.array(
[
[1.0, 0.0, 0.0, 0.0],
[0.0, 1.0, 0.0, 0.0]
]
)
# Obtain prior estimates and error covariance from initial values
self.predict()
def predict(self):
# prior state estimate
self.X = self.A @ self.X
# prior-error covariance matrix
self.P = self.A @ self.P @ self.A.T + self.B @ self.Q @ self.B.T
self.S = self.P.copy()
def update(self, measurement: tuple):
# kalman gain
self.G = self.P @ self.C.T @ np.linalg.inv((self.C @ self.P @ self.C.T + self.R))
# new state estimate
self.X = self.X + self.G @ (np.array(measurement).reshape(-1,1) - self.C @ self.X)
# new-error covariance matrix
self.P = (np.eye(self.A.shape[0]) - self.G @ self.C) @ self.P
測定値でカルマンフィルタの動作を確認します。
# あるトラックの中心座標
measured = [(477.0, 478.0), (477.5, 476.0), (483.0, 479.5), (485.0, 480.0), (486.5, 476.0), (488.0, 475.0), (490.0, 471.0), (494.0, 462.5), (495.0, 455.5), (498.0, 457.0),
(502.5, 450.0), (502.0, 449.5), (505.5, 443.0), (506.5, 444.5), (508.0, 438.5), (514.0, 439.5), (515.0, 436.0), (517.0, 435.5), (520.0, 431.0), (520.5, 428.5),
(520.5, 426.5), (520.0, 427.0), (523.0, 424.0), (526.5, 419.5), (527.5, 418.5), (528.5, 419.5), (531.0, 416.0), (531.5, 411.5), (533.5, 413.0), (535.0, 409.5),
(538.0, 410.0), (539.0, 410.5), (539.0, 407.5), (549.0, 402.5), (549.5, 398.5), (551.0, 394.5), (551.5, 392.0), (551.5, 392.5), (557.5, 389.5), (557.0, 388.5),
(558.5, 387.0), (558.5, 386.0), (560.0, 382.5), (563.5, 381.0), (564.5, 381.5), (564.5, 381.5), (567.5, 380.5), (567.5, 376.0), (575.0, 369.5), (577.0, 367.0),
(578.5, 366.5), (580.0, 363.0), (582.0, 362.5), (582.5, 361.0), (583.0, 358.5), (586.5, 359.0), (588.5, 355.5), (589.0, 356.0), (590.5, 355.0), (593.5, 353.5),
(595.5, 350.5), (596.5, 351.0), (595.0, 350.5), (596.5, 348.0), (596.5, 347.5), (597.0, 346.0), (597.0, 337.0), (598.5, 336.0), (604.5, 336.5), (605.0, 337.0),
(606.0, 333.0), (607.5, 332.0), (607.5, 331.0), (609.5, 328.0), (611.0, 328.0), (611.5, 327.5), (612.0, 324.0), (616.0, 324.5), (618.0, 322.0), (619.5, 322.5),
(620.5, 321.0), (622.5, 317.5), (621.0, 315.0), (622.0, 315.5), (622.5, 314.5), (623.5, 311.5), (624.0, 312.0), (625.5, 305.0), (636.5, 294.5), (638.0, 295.0),
(638.5, 294.0), (640.5, 293.0), (640.5, 289.5), (646.5, 289.0), (648.5, 288.5), (647.5, 288.5), (649.5, 287.5), (650.5, 286.0), (651.0, 286.5), (652.0, 286.5),
(651.5, 284.0), (651.5, 282.0), (653.0, 278.5), (653.5, 278.0), (654.5, 274.0), (656.0, 272.0), (655.0, 274.0), (657.5, 274.0), (666.0, 271.0), (667.0, 270.0),
(667.5, 268.5), (667.5, 268.5), (668.5, 265.0), (669.5, 262.0), (671.0, 261.0), (675.0, 260.0), (675.0, 261.5), (676.0, 261.0), (675.0, 258.5), (675.5, 259.0),
(678.0, 258.0), (679.0, 259.0), (679.0, 254.5), (680.0, 252.0), (679.5, 248.5), (680.0, 246.5), (684.0, 246.0), (684.0, 244.0), (686.0, 243.0), (686.0, 240.5),
(687.5, 241.0), (701.5, 222.5), (701.5, 221.5), (704.0, 220.5), (704.0, 220.0), (705.0, 217.0), (704.5, 218.0), (705.0, 219.0), (707.0, 219.0), (707.5, 217.5),
(709.0, 213.5), (710.5, 217.5), (711.5, 215.0), (712.0, 212.5), (711.5, 210.5), (714.0, 208.0), (715.0, 208.5), (714.5, 204.5), (728.0, 194.0), (729.0, 193.0),]
len(measured) # 150
マッチングできなかった場合を シミュレートし、20-29 , 81-89, 121-129 フレームを意図的にスキップさせて、軌跡を予想できるか確認します。
kf = KalmanFilter(measured[0], dt=0.1)
kf_X=[]
kf_P=[]
for n in range(len(measured)):
# Simulating the lost of tracking between 21 and 29, 81 and 89 frames
if (20 < n < 30) or (80 < n < 90) or (120 < n < 130):
kf.predict()
# 状態推定値と共分散行列を保存
kf_X.append(kf.X)
kf_P.append(kf.P)
else:
kf.predict()
kf.update(np.array([measured[n]]))
kf_X.append(kf.X)
kf_P.append(kf.P)
測定値と、カルマンフィルタで処理したデータを Dataframe にします。
# データを可視化
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
# 実測値
measured_x = np.array(measured)[:,0]
measured_y = np.array(measured)[:,1]
velocity_x = np.zeros(len(measured))
velocity_y = np.zeros(len(measured))
df_measured = pd.DataFrame(data=[measured_x, measured_y, velocity_x, velocity_y], index=['x', 'y', 'vx', 'vy'])
df_measured = df_measured.T
df_measured['data'] = 'measured'
# 推定値/更新値
filtered = np.array([X.flatten() for X in kf_X]).astype(int)
filtered_x = filtered[:,0]
filtered_y = filtered[:,1]
velocity_x = filtered[:,2]
velocity_y = filtered[:,3]
df_filtered = pd.DataFrame(data=[filtered_x, filtered_y, velocity_x, velocity_y], index=['x', 'y', 'vx', 'vy'])
df_filtered = df_filtered.T
df_filtered['data'] = 'filtered'
df = pd.concat([df_measured, df_filtered], ignore_index=True)
df
# 出力
x y vx vy data
0 477.0 478.0 0.0 0.0 measured
1 477.5 476.0 0.0 0.0 measured
2 483.0 479.5 0.0 0.0 measured
3 485.0 480.0 0.0 0.0 measured
4 486.5 476.0 0.0 0.0 measured
... ... ... ... ... ...
295 715.0 207.0 13.0 -16.0 filtered
296 716.0 205.0 13.0 -16.0 filtered
297 717.0 204.0 13.0 -16.0 filtered
298 720.0 201.0 14.0 -17.0 filtered
299 723.0 198.0 14.0 -18.0 filtered
300 rows × 5 columns
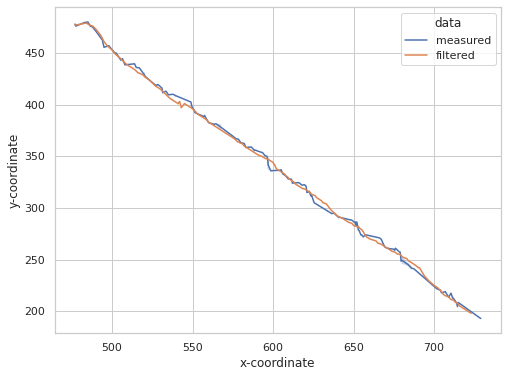
プロットします。 青色の測定値がカルマンフィルタで補正できています。また、意図的にロストさせた欠損値も予測できているようです。
fig, ax = plt.subplots(figsize=(8, 6))
sns.lineplot(
data=df,
x="x",
y="y",
hue="data",
ax=ax
)
ax.set_xlabel("x-coordinate")
ax.set_ylabel("y-coordinate")
ユークリッド距離
検出した人とトラックした人(割り当てた人)が正解であれば、両者の中心点の距離は近いであろうと予測できます。
私はユークリッド距離をその評価に使いました。しかし最終的には 「人物フレームの 幅(width)」 を 閾値にする というアバウトな閾値になりました。
検出した人によってユークリッド距離の閾値は違うので、一律に閾値を決めるのではなく動的に閾値を定めようとしたのですが、結果として 単純に人物フレームの幅を閾値にした方が良かった(ロストして無駄に登録される人の数が少なかった) ことが理由です。
この方法だと閾値に 柔軟性がないので 類似度が高く、並んで歩いている人では追跡がロストしてしまいます。
動的な閾値:95%信頼区間は閾値に使えるか(使えず)
人の移動する速度が一定であれば、検知した人 と トラックした人 の中心点のユークリッド距離は(近いはずなので)一定範囲に収まるのではないかと考えました。
ロストが多くなると その位置情報はカルマンフィルタで推定した値なので 不確実性が増しますが、ここではカルマンフィルタを信じることにして 95%信頼区間を使って 動的な閾値設定ができそうか確認しました。
# 実際にマッチした人のユークリッド距離の履歴 len(euc_distances):120)
euc_distances = [0.707, 0.5, 4.301, 1.581, 9.618, 2.062, 1.803, 2.55, 0.707, 2.693,
2.062, 0.5, 0.707, 1.118, 8.382, 7.018, 10.012, 6.0, 4.272, 3.905,
5.385, 1.803, 2.236, 1.414, 5.59, 8.5, 2.236, 6.946, 2.693, 6.5,
0.707, 2.693, 4.272, 2.0, 3.202, 3.0, 0.707, 1.581, 4.243, 2.236,
2.121, 0.707, 3.536, 1.414, 1.581, 3.041, 0.5, 3.606, 4.61, 2.693,
7.018, 5.148, 5.408, 4.272, 0.707, 3.808, 1.118, 0.5, 1.803, 1.118,
1.5, 2.55, 3.536, 3.536, 0.5, 3.905, 4.243, 2.55, 2.828, 2.062,
0.5, 1.118, 2.5, 1.581, 2.0, 2.062, 2.915, 2.55, 2.5, 3.202,
1.803, 2.915, 2.236, 6.708, 4.272, 3.536, 2.236, 2.236, 1.5, 0.5,
1.803, 2.236, 1.581, 1.0, 3.354, 3.0, 3.536, 2.693, 2.915, 2.236,
1.118, 1.581, 0.707, 1.414, 3.354, 9.925, 4.472, 2.693, 2.5, 1.581,
5.5, 4.743, 2.915, 2.915, 2.062, 3.5, 4.5, 3.202, 2.693, 2.5]
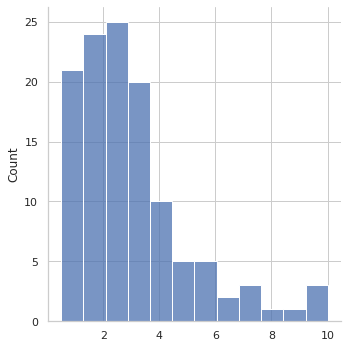
データを プロットして確認します。正規分布には見えません。データの分布を考えると 95% 信頼区間は使えないと思われます。
import pandas as pd
import seaborn as sns
from scipy import stats
sns.set(style='whitegrid')
euc_dist = pd.Series (data=euc_distances, name="euclidean distance")
sns.displot(euc_distances)
plt.show()
このデータの人の場合、stats.norm.interval で信頼区間を求めると、 -1.011396596174814 ~ 6.96906326284148 でした。実際に動画で試してみたところ 閾値が狭すぎるようで 外れ値に見える 8~10 の範囲も拾わないと、ロストと無駄な登録が多発してしまいました。
euc_distances = np.array(euc_distances)
min, max = stats.norm.interval(alpha=0.95, loc=euc_distances.mean(), scale=stats.tstd(euc_distances))
print(f"min:{min} --- max:{max}")
#出力
min:-1.011396596174814 --- max:6.96906326284148
マハラビノス距離 (実装できず)
マハラビノス距離を使うと、ユークリッド距離とは異なり、データの集合(バラツキ)を考慮して 楕円形状で 距離をとらえることができます。
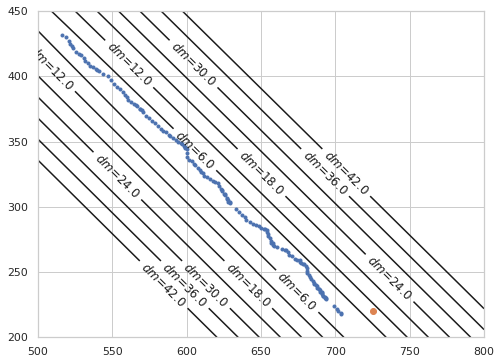
オレンジで囲った部分が マハラビノス距離での誤検知(擬陽性)です。私の実装では検出がトラックの軌道が直線の場合、マハラビノス距離が小さくなり 離れた人との誤検知が多発してしまいました。
閾値を緩めたり、算出に使用する追跡ポイントデータを 30個にしてみたり、他の条件で厳しくしたりと色々と試しましたが良い結果は出ず、実装を断念しました。

なお、実際のデータでの基本動作確認は以下のように行いました。
# ある人の移動した座標履歴 (x,y) ※カルマンフィルタを適用した値
track_points = [(516, 432), (519, 430), (521, 427), (522, 425), (523, 423), (524, 422), (526, 419), (528, 417), (529, 416), (531, 414),
(532, 412), (534, 410), (535, 408), (537, 407), (539, 406), (540, 405), (541, 404), (544, 402), (547, 400), (549, 397),
(551, 394), (553, 392), (555, 390), (557, 388), (559, 386), (560, 384), (561, 382), (563, 380), (565, 379), (566, 378),
(567, 377), (569, 375), (569, 375), (570, 374), (571, 373), (573, 370), (575, 368), (577, 366), (579, 364), (581, 362),
(583, 360), (584, 358), (586, 357), (588, 355), (589, 354), (591, 353), (593, 351), (594, 350), (596, 349), (597, 348),
(598, 347), (599, 346), (599, 345), (600, 344), (600, 341), (600, 338), (602, 336), (604, 335), (605, 333), (606, 332),
(608, 330), (609, 328), (610, 327), (611, 326), (612, 324), (614, 323), (616, 321), (618, 320), (619, 319), (621, 318),
(622, 316), (623, 314), (624, 313), (624, 312), (625, 310), (626, 310), (626, 309), (627, 307), (627, 306), (628, 305),
(628, 304), (629, 304), (629, 303), (633, 298), (635, 296), (637, 294), (639, 292), (640, 290), (643, 288), (645, 287),
(647, 286), (649, 285), (650, 284), (652, 283), (653, 283), (654, 282), (654, 281), (655, 279), (655, 278), (656, 276),
(657, 274), (657, 272), (658, 272), (658, 271), (659, 270), (661, 269), (664, 268), (666, 267), (667, 267), (668, 265),
(669, 263), (671, 262), (673, 260), (674, 259), (676, 259), (676, 258), (677, 257), (678, 256), (679, 256), (680, 255),
(681, 253), (681, 251), (681, 249), (682, 248), (683, 246), (684, 245), (685, 243), (686, 242), (686, 241), (687, 240),
(688, 239), (688, 238), (689, 237), (689, 237), (690, 236), (690, 235), (691, 235), (691, 234), (691, 233), (692, 232),
(692, 232), (693, 231), (693, 230), (694, 230), (694, 229), (699, 224), (701, 222), (702, 220), (704, 219), (704, 218) ]
まず、Town Centre の動画では人の軌跡はほぼ直線なので、等高線と一緒にプロットすると以下のようになります。
## https://qiita.com/MasafumiTsuyuki/items/de19d8ec274e961ec946
# z軸値 (標本平均からのマハラノビス距離) を計算
import seaborn as sns
import numpy as np
from matplotlib import pyplot as plt
from scipy.spatial import distance
tp = np.array((track_points))
cov = np.cov(tp.T)
mean = np.mean(tp, axis=0)
mdist = np.zeros((100, 100, 3))
# 2点間 (track_pointの最近の座標と、範囲指定した座標における、マハラビノス距離
for n, i in enumerate(np.linspace(500,800,100)):
for m, j in enumerate(np.linspace(200,450,100)):
mdist[n][m] = (i, j, distance.mahalanobis([i,j], tp[-1], np.linalg.pinv(cov)))
plt.figure(figsize=(8, 6))
cont = plt.contour(mdist.T[0], mdist.T[1], mdist.T[2], levels=[6, 12, 18, 24, 30, 36, 42], colors="k")
cont.clabel(fmt='$dm$=%1.1f', fontsize=12)
# 測定値が外れ値だった場合
det = np.array((725, 220))
plt.plot(tp[:,0], tp[:,1], '.')
plt.plot(det[0], det[1], 'o')
plt.show()
また、外れ値をプロットすると(上画像のオレンジの点)マハラビノス距離が大きくなっているのが分かります。
次に 実際の動きを想定して、フレーム毎に 測定値と最新の予測値のマハラビノス距離を確認します。
# 測定値が外れ値だった場合
det = np.array((725, 220))
tp_copy = track_points.copy()
# 外れ値を追加してマハラビノス距離を取る
tp_copy.append(det)
mdist_list = []
for i, _ in enumerate(tp_copy):
tp = tp_copy[:i+1]
# 追跡した座標の数が 3より多ければ、マハラビノス距離を計算。それ以外は、 1とする
if len(tp) > 3:
cov = np.cov(np.array(tp).T)
mdist_list.append(distance.mahalanobis(tp[i], tp[i-1], np.linalg.pinv(cov)))
else:
mdist_list.append(1.0)
plt.figure(figsize=(8, 6))
plt.plot(mdist_list)
plt.show()
追加した外れ値のマハラビノス距離は 8.04 となり、異常値として検知できています。
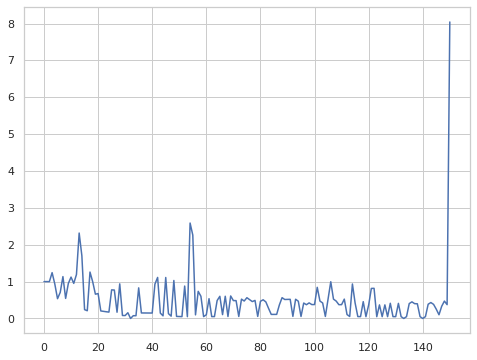
それ以外は 3 より小さいので以下にある DeepSORT のコメントを参考に 閾値を 5.9915 にすればいけそう!と 動画で試しましたが 誤検知(擬陽性)が多く、デバックできず、、、力尽きました。(閾値を 9.4877 にしても改善には至らず)
A suitable distance threshold can be obtained from
chi2inv95. If
only_positionis False, the chi-square distribution has 4 degrees of freedom, otherwise 2.
https://github.com/theAIGuysCode/yolov4-deepsort/blob/master/deep_sort/kalman_filter.py
マハラビノス距離は非常に有用な異常検知手法なので是非実装したかったです。残念です。
Memo: DeepSORT では、マハラビノス距離を カルマンフィルタで得られる 共分散行列から求め、閾値を超えたものについてコストを高くし除外するゲート処理が行われています4
描画
描画について工夫した点です。
1. 人が重なった場合
人が重なった場合 良い結果にならないので マッチング処理をスキップするようにしています。視覚的に動作を確認できるようにしました。

2. トラックがLostした場合でも 追跡ポイント や BBox を描画
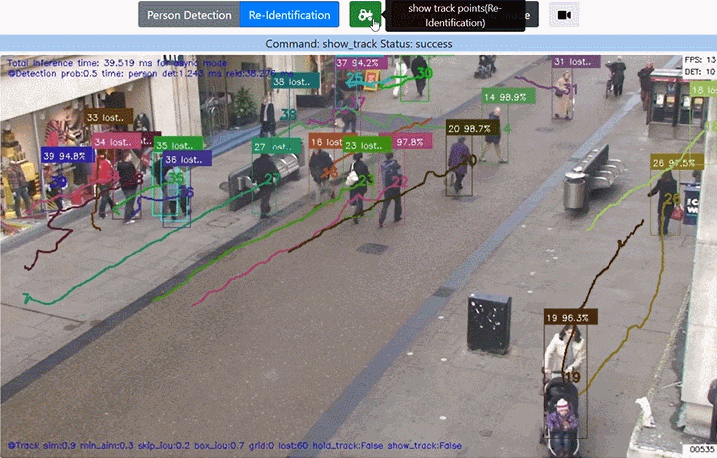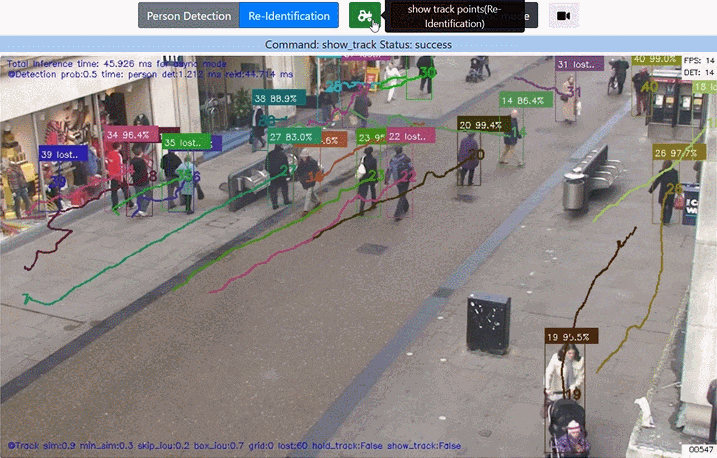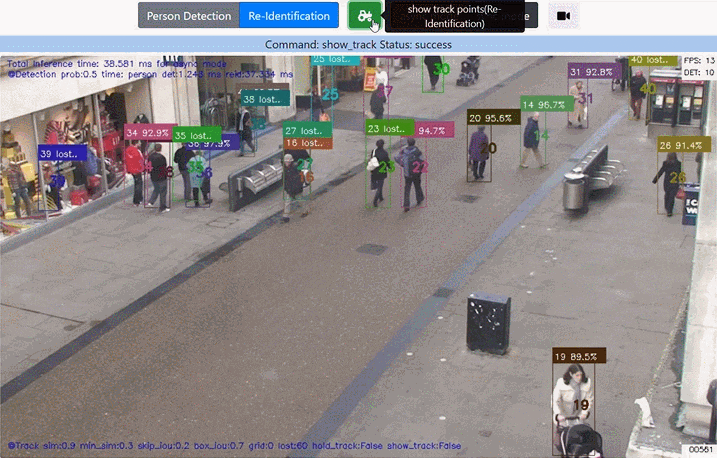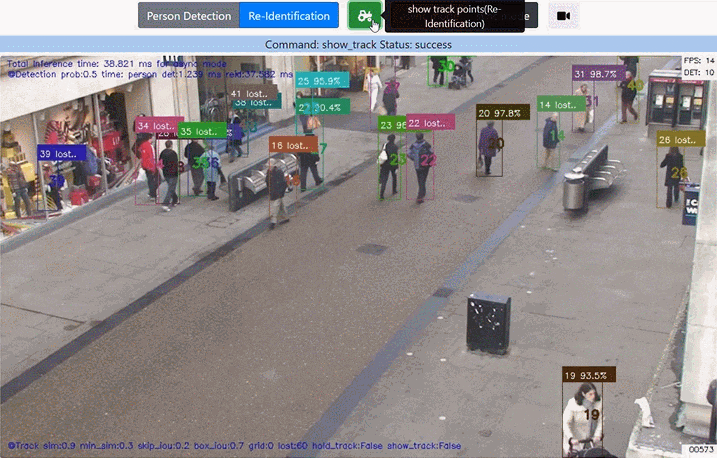
真ん中の自転車を押している人は 結構な頻度で Lost していますが(そもそも人して検出されない場合もある)、その場合でも カルマンフィルタの予測を用いて BBoxや追跡ポイント を描画しています。Lostしたことが分かるように「信頼度」の部分に "Lost.." の文字を表示します。
人がLostする度にBBox と追跡ポイントが消える現象 (目がチカチカする) を防ぐこともできます。

3. 追跡ポイント描画のON/OFF
トグルボタンで 追跡ポイント描画 を ON/OFFできるようにしました。追跡ポイントの描画でカオス状態に見える動画も、描画を外すとすっきり見えて違った印象になります。
最後に
最後に私のPCで Oxford Town Centre の動画を DeepSORT と OpenVINO のC++デモプログラム で実行した動画の YouTubeリンクを載せておきます。
リポジトリのプログラムは複数のクラスを指定して(人、車など)、マルチオブジェクトトラッキングができます。ロジックが洗練されていてプログラムの行数が少ないのも驚きです。
「この場面どうやって追跡しているの?」という場面がたくさんあります。最終的に登録された人は 369 名 (私のは 516名) 。誤検知(偽陰性)が少なく、割り当て精度が高いことを意味します。時間があるときにもう少しロジックを研究してみたい。
最後まで読んでくださりありがとうございました。
環境
- OpenVINO Toolkit 2020.1 ~ 2021.41
- Windows10 (Intel(R) Core(TM) i5-7200 CPU @ 2.50Ghz)
参考サイト一覧
感謝です。
-
https://www.kaggle.com/datasets/ashayajbani/oxford-town-centre?select=TownCentreXVID.mp4 ↩
-
https://www.pexels.com/video/people-on-the-escalators-of-a-mall-1338590/ ↩
-
scipy.optimize import linear_sum_assignmentよりもMunkresの方が 少し割当精度(最終的に登録された人の数が少ない) が良かったため。 ↩ -
DeepSORT「Invalidate infeasible entries in cost matrix based on the state distributions obtained by Kalman filtering.」 ↩