モチベーション
※本記事は以前の記事の誤りを再度訂正するものである。あの記事は問題と誤解がある。
データ分析で分布を調べることは基礎的な手順のひとつであるが、1次データが常に手に入るとは限らない。特に調査会社のレポートはRAWデータなしの分位数データしか手に入らないことも多いはず。分位数のデータから分布を予測する方法をメモ代わりに記しておきたい。さらにはデータ測定には打ち切りがありことや、確率分布が出現する値(台)についても注意を払うべきであろう。
パッケージインストールとデータ読み込み
using Distributions,StatsPlots,Statistics,DataFrames,CSV
using Turing,LinearAlgebra
北海道マラソン2024 完走タイム別人数分布表
今年も北海道マラソンが開催されるので、ひきつづきこれを事例にしてみる。北海道マラソン運営はスタートから10分刻みの完走タイム別人数分布表を公開している。発表データを以下に転記する。報道によると参加者は1万7705人だったので、2562名は完走できなかったようだ。
| タイム範囲 | 男子 | 女子 | オープン | 合計 |
|---|---|---|---|---|
| 2:10:01~2:20:00 | 10 | 0 | 0 | 10 |
| 2:20:01~2:30:00 | 19 | 0 | 0 | 19 |
| 2:30:01~2:40:00 | 34 | 6 | 0 | 40 |
| 2:40:01~2:50:00 | 92 | 4 | 0 | 96 |
| 2:50:01~3:00:00 | 152 | 12 | 0 | 164 |
| 3:00:01~3:10:00 | 174 | 14 | 1 | 189 |
| 3:10:01~3:20:00 | 326 | 19 | 2 | 347 |
| 3:20:01~3:30:00 | 446 | 43 | 1 | 490 |
| 3:30:01~3:40:00 | 416 | 52 | 2 | 470 |
| 3:40:01~3:50:00 | 506 | 77 | 4 | 587 |
| 3:50:01~4:00:00 | 731 | 102 | 5 | 838 |
| 4:00:01~4:10:00 | 612 | 103 | 5 | 720 |
| 4:10:01~4:20:00 | 694 | 111 | 11 | 816 |
| 4:20:01~4:30:00 | 816 | 142 | 9 | 967 |
| 4:30:01~4:40:00 | 796 | 154 | 14 | 964 |
| 4:40:01~4:50:00 | 799 | 168 | 24 | 991 |
| 4:50:01~5:00:00 | 920 | 248 | 31 | 1,199 |
| 5:00:01~5:10:00 | 658 | 189 | 18 | 865 |
| 5:10:01~5:20:00 | 791 | 229 | 24 | 1,044 |
| 5:20:01~5:30:00 | 832 | 197 | 30 | 1,059 |
| 5:30:01~5:40:00 | 821 | 224 | 49 | 1,094 |
| 5:40:01~5:50:00 | 863 | 253 | 59 | 1,175 |
| 5:50:01~ | 780 | 179 | 40 | 999 |
| 男子 | 女子 | オープン | 完走者合計 | 未完走者 | 出走者 |
|---|---|---|---|---|---|
| 12,288 | 2,526 | 329 | 15,143 | 2,562 | 17,705 |
完走者の度数表を作成する
df = CSV.read("hokkaido-marason_2024.csv",DataFrame)
df.ac_male = accumulate(+, df[:,:male])
df.ac_female = accumulate(+, df[:,:female])
runner = df[:,:male] .+ df[:,:female] .+ df[:, :open]
df.ac_runner = accumulate(+, runner)
df.percentile_runner = df.ac_runner ./ 17705 #出走者全員
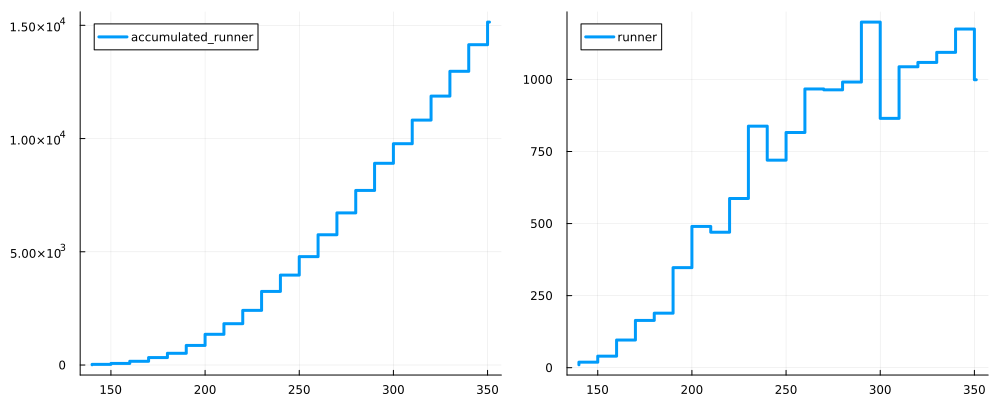
グラフからWeibull分布を仮定する
マラソン記録は低いタイムが多く存在し、高い記録が少ない。そのため分布は左右対称ではない。ここではWeibull分布を想定してみたい。Weibull分布は故障率で使われることが多いが、本質的にはある出来ことが成就(完成だったり故障だったり)するまでの時間分布と考えることができる。また記録は6時間(360分)で打ち切りが設定されていることも注意しなければならない。¶
p1 = @df df plot(st=:steppre,:goal_time,[:ac_male,:ac_female], label=["ac_male" "ac_female"], lw=3)
p2 = @df df plot(st=:steppre,:goal_time,[:male,:female], label=["male" "female"], lw=3)
plot(p1,p2, size=(1000,400))
モデルの作成
モデルに渡すデータは時間区分と度数分布のVectorデータである。Weibull分布の台は0~有限時間であることに対して、マラソンの記録は何らかの物理的な制約がある。世界記録でも2時間を切るのはしばらく先になりそうだし。したがってモデルには物理的な障壁(lm)も推定させる必要がありそうだ。もしくは測定の下限である170分を引いたデータを渡すこともありだろう。また測定打ち切り(u_limit)が6時間(360分)に設定されていることも反映している。
@model function fqweibull(tim, acc ; u_limt=360, n=length(tim), )
lm ~ truncated(TDist(3), 60, 230)
a ~ truncated(TDist(2), 1e-3, Inf)
θ ~ InverseGamma(2,3)
s ~ Exponential(1)
dist = truncated(Weibull(a, θ) ; upper = u_limt)
tim ~ arraydist([Normal(quantile(dist, q) + lm, s ) for q in acc])
end
Turingでパラメータを探す
モデルが作成されたらNUTS()でサンプリングを行う。
times =df[1:(end-1),:goal_time]
quant =df[1:(end-1),:percentile_runner]
c_quantile = sample(fqweibull(times,quant),NUTS(),3000)
Chains MCMC chain (3000×4×1 Array{Float64, 3}):
Iterations = 1001:1:4000
Number of chains = 1
Samples per chain = 3000
Wall duration = 3.03 seconds
Compute duration = 3.03 seconds
parameters = lm, a, θ, s
internals =
Summary Statistics
parameters mean std mcse ess_bulk ess_tail rhat ess_per_sec
Symbol Float64 Float64 Float64 Float64 Float64 Float64 Float64
lm 124.9373 2.0190 0.0683 874.4969 1292.3242 0.9997 288.7081
a 3.1006 0.0649 0.0021 949.3115 1440.3143 0.9998 313.4076
θ 196.6165 2.0047 0.0651 944.0560 1122.7947 0.9997 311.6725
s 1.7503 0.2972 0.0091 996.7565 666.3171 1.0002 329.0711
Quantiles
parameters 2.5% 25.0% 50.0% 75.0% 97.5%
Symbol Float64 Float64 Float64 Float64 Float64
lm 120.9525 123.5922 124.9787 126.2671 128.7652
a 2.9765 3.0568 3.1000 3.1432 3.2299
θ 192.7589 195.2666 196.5504 197.9681 200.5981
s 1.2656 1.5438 1.7121 1.9214 2.4396
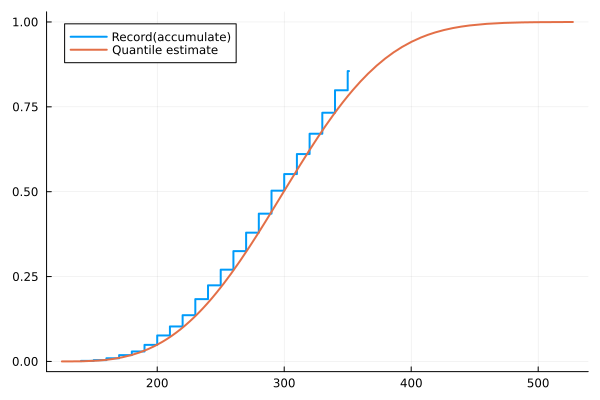
推定結果をグラフ化して比較してみる
わりとうまくフィットした感じがする。
runner_param = get(c_quantile,[:a, :θ]) |> t-> (mean(t.a), mean(t.θ))
runner_lm = get(c_quantile,[:lm]) |> t-> mean(t.lm)
@df df plot(:goal_time , :percentile_runner, st=:steppre, label="Record(accumulate)",lw=2,legend=:topleft)
plot!(Weibull(runner_param...) .+ runner_lm ,func=cdf,lw=2,label="Quantile estimate")
ランナーの性別記録は正確な度数がわからない
性別データも同じくできればいいが、実際は未完走者が2,562名(約15%)おり、その一部が男性であろうという情報だけなので、男性の出走者数(完走者じゃないよ)がわからないのである。未完走者は何かしらの事情で非常に長い時間がかかってしまった人とみなすなら、この情報をモデルに組み込むことができる。
【変更点】
・おおよそ未完走者の割合は15%程度
・入力データとして累積時間別の人数を渡し、モデル内で計算
・Weibullの切り捨て(Truncated)をやめて、未完走者は測定時間幅の右側外と考える
・完走者合計(goal_sum)を因数として渡す
@model function fqweibull(tim, acx , goal_sum ; u_limt=360, n=length(tim))
#未完走者推定
retire ~ truncated( Normal( 0.15 * (12288/(1 - 0.15)), 1000) , 0, 2562)
ac_quant = [ ac / (retire + goal_sum) for ac in acx]
lm ~ truncated(TDist(3), 60, 160)
a ~ truncated(TDist(2), 1e-3, Inf)
θ ~ InverseGamma(2,3)
s ~ Exponential(1)
# dist = truncated(Weibull(a, θ) ; upper = u_limt)
dist = Weibull(a, θ)
tim ~ arraydist([Normal(quantile(dist, q) + lm, s ) for q in ac_quant])
return ac_quant
end
times =df[1:(end-1),:goal_time]
ac_xs =df[1:(end-1),:ac_male]
m_chain = sample(fqweibull(times,ac_xs, df.ac_male[end]),NUTS(),3000)
Chains MCMC chain (3000×17×1 Array{Float64, 3}):
Iterations = 1001:1:4000
Number of chains = 1
Samples per chain = 3000
Wall duration = 3.72 seconds
Compute duration = 3.72 seconds
parameters = retire, lm, a, θ, s
internals = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
Summary Statistics
parameters mean std mcse ess_bulk ess_tail rhat ess_per_sec
Symbol Float64 Float64 Float64 Float64 Float64 Float64 Float64
retire 2336.7841 199.2009 4.9968 1272.4537 934.2466 1.0010 342.0574
lm 123.8325 3.9260 0.1195 1112.8539 1161.1553 1.0010 299.1543
a 3.0735 0.1262 0.0038 1149.4288 1156.5061 1.0013 308.9862
θ 194.8638 4.0151 0.1167 1183.7661 1216.4229 1.0010 318.2167
s 3.2534 0.4987 0.0118 1833.2027 1666.6718 0.9997 492.7964
Quantiles
parameters 2.5% 25.0% 50.0% 75.0% 97.5%
Symbol Float64 Float64 Float64 Float64 Float64
retire 1839.9728 2232.9428 2392.9250 2491.6245 2556.6401
lm 115.4712 121.3094 124.0152 126.5734 130.8725
a 2.8568 2.9851 3.0627 3.1498 3.3475
θ 187.1262 192.2186 194.8715 197.4774 202.8322
s 2.4203 2.9071 3.2009 3.5524 4.3799
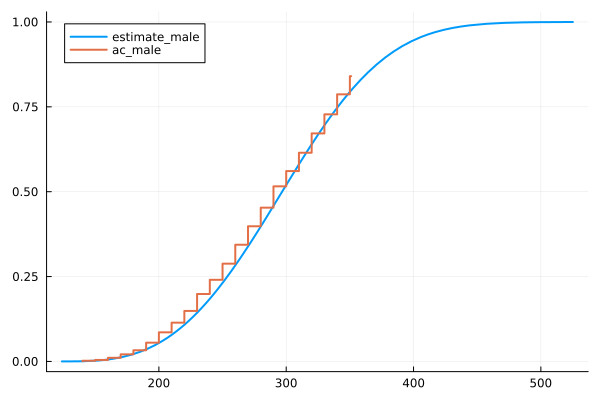
グラフ化して予測値と実測を比べる
male_param = get(m_chain, [:a, :θ]) |> t-> (mean(t.a), mean(t.θ))
male_lm = get(m_chain,[:lm]) |> t-> mean(t.lm)
male_retire = get(m_chain,[:retire]) |> t-> mean(t.retire)
@df df plot(Weibull(male_param...) .+ male_lm, func=cdf, label="estimate_male", lw=2)
@df df plot!(:goal_time, :ac_male ./ ( :ac_male[end] + male_retire) , st=:steppre, label="ac_male", lw=2)
うまく推定できたようだがどうだろう。推定したWeibull分布をつかって95%域を推定することができる。約400分(6時間40分)まで走れるようにすれば、男性出走者の約95%が完走できるようになるかもしれない。
quantile(truncated(Weibull(male_param...), 0, 360), [0.95])[1] + male_lm