LoginSignup
0
0

More than 1 year has passed since last update.

@kimseok1973(マツヤマ テツ)

Turing.jlで度数分布／分位数（Quantile）からパラメータを推定する

Last updated at Posted at 2022-08-13

モチベーション

データ分析で1次データが常に手に入るとは限らない。特に調査会社のレポートはRAWデータを有料化するため、おおまかな度数分布でしか発表しないことが多い。限られたデータ（度数分布／分位数）からサンプルの分布を調べることを、普段遊んでいるTuring.jlでやりたい。

度数分布とは？

こういうデータです。調査会社のレポートは基本こんな感じ。

①階級 ②階級値 ③度数 ④相対度数 ⑤累積相対度数
0以上50未満 25 24 0.5106 0.5106
50以上100未満 75 14 0.2979 0.8085
100以上150未満 125 2 0.0426 0.8511

パッケージインストールとデータ読み込み

    using Distributions,Turing
    using Statistics,DynamicPPL,DataFrames,CSV,NamedArrays
    using StatsPots

Toyモデルで課題を作る。
自前で調査すれば1次データとしてRAWデータがあるので観測サンプル（Observed）から分布を推計することができる。

    ss = rand(Normal(2.3,1.3),200);
    
    @model function demo(xs)
        m ~ Normal(0,3)
        s ~ InverseGamma(2,3)
        xs .~ Normal(m,s)
    end
    ctest = sample(demo(ss),NUTS(),3000)

    Summary Statistics
      parameters      mean       std   naive_se      mcse         ess      rhat    ⋯
          Symbol   Float64   Float64    Float64   Float64     Float64   Float64    ⋯
               m    2.2848    0.0902     0.0016    0.0016   2891.5669    0.9999    ⋯
               s    1.2712    0.0661     0.0012    0.0014   2947.7377    0.9998    ⋯

しかし入手できるデータがRAWデータではなく次のような分位数（quantile)データだけの場合がある。

A ╲ B 0.25 0.5 0.75 0.95
Quantile 1.44301 2.30823 3.05904 4.16651

度数分布表から分布のパラメーターを調べるモデルは次のように書ける。基本的にはquantileで累積相対度数に対応する階級値を探すという考え。

    @model function q_demo()
        m ~ Normal(0,3)
        s ~ InverseGamma(2,3)
        dist = Normal(m,s)
        q25 ~ Normal(quantile(dist,0.25),0.2)
        q50 ~ Normal(quantile(dist,0.5),0.2)
        
        q25 ~ Normal(qs[1],0.1)
        q50 ~ Normal(qs[2],0.1)
    end
    qtest = sample(q_demo(),NUTS(),3000)

あるいはこういう書き方も可能。TuringチームのFjeldeからのアドバイス。

    @model function prob_demo()
        m ~ Normal(0,3)
        s ~ InverseGamma(2,3)
        dist = Normal(m,s)
        q25 = quantile(dist,0.25)
        q50 = quantile(dist,0.5)
        
        # This code is suggestied by torfjelde(Tor Erlend Fjelde)
        # see this page.
        # https://discourse.julialang.org/t/turing-jl-prior-on-quantiles/59510/2
        DynamicPPL.@addlogprob! logpdf(Normal(qs[1],0.1), q25 )
        DynamicPPL.@addlogprob! logpdf(Normal(qs[2],0.1), q50 )
    end
    qtest = sample(prob_demo(),NUTS(),3000)

うまく推定できた。

    Summary Statistics　
    parameters      mean       std   naive_se      mcse         ess      rhat    ⋯
      Symbol   Float64   Float64    Float64   Float64     Float64   Float64    ⋯
           m    2.3643    0.1019     0.0019    0.0030   1057.9797    1.0011    ⋯
           s    1.3659    0.2104     0.0038    0.0065   1084.1405    1.0016    ⋯

うまく推定できることが分かったので、実際の問題の解決してみる。
（実はGamma分布はこういう風に使えない。SpecialFunctions.jlのgamma_inc_inv関数が自動微分（ForwardDiff.jl）に対応していないようで。これを回避する方法については別の記事を書きます）

マラソン大会の人員手配を考える

北海道マラソン２０２２がもうすぐ開催されるのでこれを課題にしてみよう。
マラソンの出展ブースで完走者全員に記念品を手渡したい。ランナーたちはスタートから2時間～6時間で到着する。スタッフを雇う時間は限られているので、ランナーがもっとも多くゴールする時間帯にあわせてスタッフを集めたい。もっとも多くのランナーが到着するのはスタートから何分ごろと考えるべきだろうか？

北海道マラソンは2019年大会の完走タイム別人数分布表をホームページで公開している。残念ながらRAWデータはなくスタートから2時間～4時間までは10分刻みの階級になっているが、4時間～5時間のランナーはひとつ階級で表示されている。2019年は最終ランナーの締め切りが300分（5時間）となっており（2019年大会は制限時間5時間でしたが、2022年大会は6時間になりました）北海道マラソン2019の参加者は公式で15,932人と発表されていることから、5時間の制限時間に合わなかった2,475人がいるようだ。この点を反映してまとめたのが下記の表である。

タイム（分） 男子 女子 合計
～140 29 0 29
141～150 25 0 25
151～160 83 5 88
161～170 127 7 134
171～180 281 11 292
181～190 268 26 294
191～200 470 36 506
201～210 648 60 708
211～220 697 86 783
221～230 818 117 935
231～240 1,112 180 1,292
241～300 6,779 1,592 8,371
301～ 不明 不明 2,475

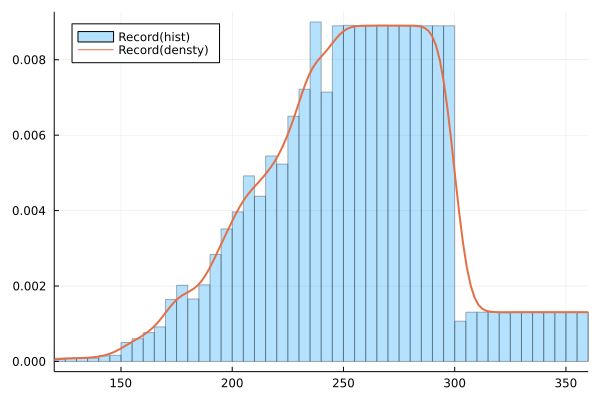
上記のデータでdensityグラフを生成し分布を把握する。最終ランナーは301分～420分に設定した。

    mean_f = [120,141,151,161,171,181,191,201,211,221,231,241,301]
    mean_t = [140,150,160,170,180,190,200,210,220,230,240,300,420]
    mean_record = [collect(range(mean_f[i],mean_t[i] ; length=df[i,:runner])) for i = 1:13]  |> t -> vcat(t...)
    histogram(mean_record,normalize=:pdf,label="Record(hist)",xlims=(120,360),alpha=0.3)
    density!(mean_record,label="Record(densty)",lw=2,legend=:topleft)

hokkaido-M_record.png

予想どおり241分以降のデータが欠落しているのでいびつな形になっている。ランナーの到着を標準分布と仮定しそのパラメータを調べたい。

度数分布データから分布のパラメータを推定する

まずはデータをCSVで作成しDataFrameに読み込んで累積相対度数のデータに修正する。

    df = CSV.read("hokkaido-marason.csv",DataFrame)
    df = df[:,Not([:male,:female])]
    push!(df,[420,2475])
    df.run_accum = accumulate(+,df[:,:runner])
    df.run_accum_quantile = df.run_accum ./ 15932

これで次のようなDataFrameを作ることができる。

id goal_time runner run_accum run_accum_quantile
1 140 29 29 0.00182024
2 150 25 54 0.0033894
3 160 88 142 0.00891288
4 170 134 276 0.0173236
5 180 292 568 0.0356515
6 190 294 862 0.0541049
7 200 506 1368 0.0858649
8 210 708 2076 0.130304
9 220 783 2859 0.17945
10 230 935 3794 0.238137
11 240 1292 5086 0.319232
12 300 8371 13457 0.844652
13 420 2475 15932 1.0

データが用意できたのでmodelを書く。

    @model function findfromquantile(tim,acc)
        n = length(tim)
        μ ~ InverseGamma(2,3)
        σ ~ InverseGamma(2,3)
        s ~ Truncated(Normal(0,3),0,10)
    
        dist = Normal(μ,σ)
        q = Vector{Any}(undef,length(acc))
        for i = 1:n
            q[i] ~ Normal(quantile(dist,acc[i]),s)
            q[i] ~ Normal(tim[i],s)    
        end
    end
    model = findfromquantile(df[1:(end-1),:goal_time],df[1:(end-1),:run_accum_quantile])
    c_quantile = sample(model,NUTS(),3000)

注意点としては累積相対度数が1.0になるところは外す。当たり前だが100％になる度数は何でもありなのでパラメータ探索に失敗する。

    summary_report, quantile_report = describe(c_quantile[:,[:μ,:σ],:])

    Summary Statistics
      parameters       mean       std   naive_se      mcse         ess      rhat   ⋯
          Symbol    Float64   Float64    Float64   Float64     Float64   Float64   ⋯
               μ   257.5399    1.1390     0.0208    0.0262   1868.9463    1.0022   ⋯
               σ    41.0041    0.6355     0.0116    0.0138   1800.3685    1.0016   ⋯
    Quantiles
      parameters       2.5%      25.0%      50.0%      75.0%      97.5% 
          Symbol    Float64    Float64    Float64    Float64    Float64 
               μ   255.2174   256.8034   257.5737   258.2784   259.7486
               σ    39.7112    40.6044    41.0198    41.4147    42.2425

うまく収束したようだ。平均値の95％確信区間255分～260分というのが分かった。

    m_1 = get(c_quantile,[:μ]).μ |> mean
    o_1 = get(c_quantile,[:σ]).σ |> mean
    quantile_est_dist = Normal(m_1,o_1)
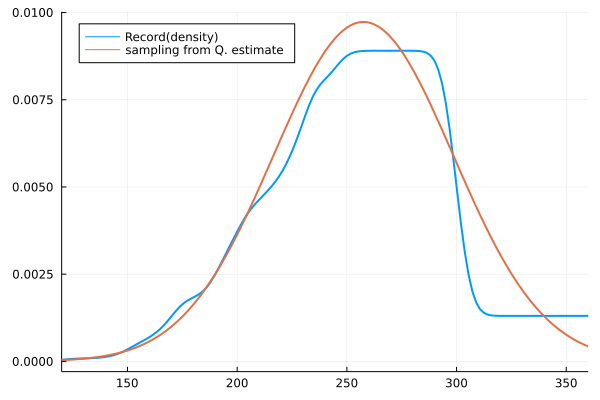
    density(mean_record,lw=2,label="Density of Record",legend=:topleft,xlims=(120,360))
    plot!(quantile_est_dist,lw=2,label="Quantile estimate")

quantile-estimate.png

グラフで実際の記録と比較したとき、データとして不明であった241分以降の分布もうまく説明できているように見える。cdf（累積分布関数）を適用することで理論値と記録値を比較してもうまくフィットしているようだ。

df.run_quantile_cdf=cdf(quantile_est_dist,df[:,:goal_time]);df
goal_time runner run_accum run_accum_quantile run_quantile_cdf
1 140 29 29 0.00182024 0.0020749
2 150 25 54 0.0033894 0.00436225
3 160 88 142 0.00891288 0.00868485
4 170 134 276 0.0173236 0.0163842
5 180 292 568 0.0356515 0.0293101
6 190 294 862 0.0541049 0.0497634
7 200 506 1368 0.0858649 0.0802676
8 210 708 2076 0.130304 0.123147
9 220 783 2859 0.17945 0.17996
10 230 935 3794 0.238137 0.250907
11 240 1292 5086 0.319232 0.334413
12 300 8371 13457 0.844652 0.849784
13 420 2475 15932 1.0 0.999963

スタートから255分～260分にスタッフを重点的に集める必要があると分かった。以上。

0
0
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0