次元と近似の話。
100次元空間にプロットAがあるとする。
しかし、我々には限られた測定手段しかない。
そう。たった10通りの方法=10次元のパラメータしか測れない
そうすると、100次元空間のプロットAは10次元空間に近似して表現される。
この近似は、残りの90次元の情報を捨てているという意味ですね。
ところで、手元にある10次元のパラメータは、一般には、互いに独立ではないですね。
今日の歩数$α$と、ラーメン摂取量$β$、体重変化量$γ$と、は、互いに独立ではない。
で、ポイントは、$α, β, γ$をジックリ調べてみる。
\begin{eqnarray}
α&=&11000, \\
β&=&0, \\
γ&=&1
\end{eqnarray}
何か怪しい。
良く歩いている。ラーメンを食べていない。なのに体重が1kgも増えている。
さては、ビールをがぶ飲みしながら揚げ物を食べまくったな。
きっと、財布の中身も減っているでしょう。
つまり、パラメータ間の相関関係を仮定する事で、測定していない(次元)情報を推定できる。
関数の見方を変える。
例えば、
\begin{eqnarray}
Y &\sim& X+N(0, 0.5)\\
\Longleftrightarrow \
Y&\sim& N(X, 0.5) \tag{1}
\end{eqnarray}
として、10回の観測を行う。
set.seed(5)
N <- 10
x <- seq(1, 10, length = N)
y <- x + rnorm(N, 0, 0.5)
round(cbind(x,y), 3)
x y
[1,] 1 0.580
[2,] 2 2.692
[3,] 3 2.372
[4,] 4 4.035
[5,] 5 5.856
[6,] 6 5.699
[7,] 7 6.764
[8,] 8 7.682
[9,] 9 8.857
[10,] 10 10.069
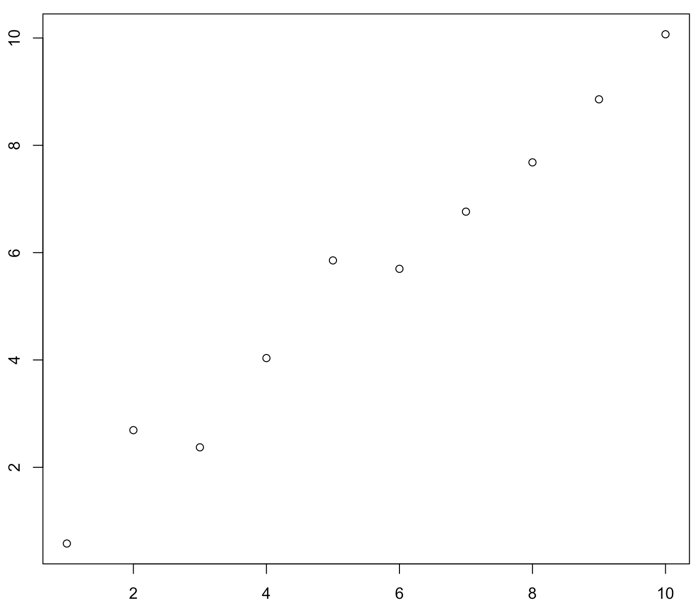
これは、真のモデル$Y=X$から誤差を含めて観測された系列データの様に見える。
でも、互いに相関のある10個のパラメータで定義された(10次元空間中の)1点と考えても良いハズだ。
前節の議論に基づくと、この既知パラメータの相関関係が推定できれば、非観測パラメータ(i.e. $x=11$の時の$y$の値)の予測分布が得られるんじゃないか。
例では$x$を離散的に取ったけれども、
x y
[1,] 0.5 0.080
[2,] 1.0 1.692
[3,] 1.5 0.872
[4,] 2.0 2.035
[5,] 2.5 3.356
[6,] 3.0 2.699
[7,] 3.5 3.264
[8,] 4.0 3.682
[9,] 4.5 4.357
[10,] 5.0 5.069
これも立派な10次元空間中の1点ですよね。
このままxの間隔を無限に細かくして、xの範囲を無限に大きくしたらどうなるか。
それは、線ですよね。
でも、無限次元空間中の1点ですよね。
つまり、ですね。
x y1 y2 y3 y4 y5
[1,] 1 0.580 1.614 1.450 1.158 1.775
[2,] 2 2.692 1.599 2.471 2.555 1.599
[3,] 3 2.372 2.460 3.734 4.108 2.963
[4,] 4 4.035 3.921 4.353 4.609 4.948
[5,] 5 5.856 4.464 5.410 5.740 4.772
[6,] 6 5.699 5.931 5.853 6.476 6.281
[7,] 7 6.764 6.701 7.709 6.495 6.556
[8,] 8 7.682 6.908 8.749 7.000 7.770
[9,] 9 8.857 9.120 8.671 8.119 8.638
[10,] 10 10.069 9.870 9.574 9.929 9.965
これは、2次元中の1本の線から誤差込みで観測された5本のサンプル、と同時に、
x=1 x=2 x=3 x=4 x=5 x=6 x=7 x=8 x=9 x=10
y1 0.580 2.692 2.372 4.035 5.856 5.699 6.764 7.682 8.857 10.069
y2 1.614 1.599 2.460 3.921 4.464 5.931 6.701 6.908 9.120 9.870
y3 1.450 2.471 3.734 4.353 5.410 5.853 7.709 8.749 8.671 9.574
y4 1.158 2.555 4.108 4.609 5.740 6.476 6.495 7.000 8.119 9.929
y5 1.775 1.599 2.963 4.948 4.772 6.281 6.556 7.770 8.638 9.965
10次元空間中の1点から誤差込みで得られた5点のサンプル、とも言える。
後者の解釈において、真のモデル$Y=X$を推定する作業は、
10次元空間座標から無限次元パラメータの相関関係を推定する事に他ならない。
これ、前節で出てきたヤツですね。
手元にある情報からパラメータ間の相関関係を仮定する事で、測定していない(次元)情報を推定するという話。
そんな事、できんのかいな。
ちなみにこのサンプルの場合は、Yは多次元正規分布から得られた点の集合になる。
おっと、そうか。そうだった。
GPMLから引用
A Gaussian process is a generalization of the Gaussian probability distribution. Whereas a probability distribution describes random variables which are scalars or vector (for multivariate distributions), a stochastic process governs the properties of functions.
復習の多次元正規分布。
承前:条件付き多変量正規分布
n次元正規分布に従う集合$Y$を、
Y\sim{}N_n(μ, \Sigma) \tag{2}
とする。
$μ$は期待値、$\Sigma$は分散共分散行列。
同一の$Y$から発生した互いに素なデータ$Y_1$と$Y_2$を考える。
$Y_1$が$Y$のうち最初の$n_1$個の要素で、$Y_2$が残りの$n_2=n-n_1$個の要素で構成されているとしても、一般性は失わない。
\begin{bmatrix}Y_1 \\ Y_2\end{bmatrix} \sim N_n\begin{pmatrix}
\begin{bmatrix}\mu_1\\\mu_2\end{bmatrix},
\begin{bmatrix}\Sigma_{11} & \Sigma_{12}\\\Sigma_{21} & \Sigma_{22}\end{bmatrix}\end{pmatrix}
$Y_1$と$Y_2$は、同一の分布から派生しているので、当然、独立ではなく、下記のカンケイを持つ。
Y_2\ |\ Y_1 \sim{} N_{n_2}(μ_{2|1},\ \Sigma_{22|1})
ここで、
\begin{eqnarray}
μ_{2|1} &=& μ_2+\frac{\Sigma_{21}}{\Sigma_{11}}(Y_1-μ_1)\\
\Sigma_{22|1} &=& \Sigma_{22}-\Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12} \tag{3}\\
\end{eqnarray}
と表せる。
これに従えば、$Y_1$から推定された$μ_1$と$\Sigma_1$を用いて$Y_2$の分布を推定できるハズ。
でも、$Y_2$が未知なのに分散共分散行列って求められないじゃん。
まてまて、特徴量の内積だよな。
なら、適切に設計されたカーネル関数のグラム行列$K$で表現できるハズ。
復習のカーネル。
$d$個のパラメータ(特徴量)で定義される関数$f(x)$は、カーネル関数$k(x_i,x_j)$を使う事で、データ数$n$個の重み付け$w$を推定することになる。というのがカーネルトリックの理屈でした。
このカーネル関数の設計を工夫すると無限のパラメータ(特徴)を考慮できる。
例えば、
k(x_i, x_j)=α\ \mathrm{exp}\left(-\beta\ ||x_i-x_j||^2\right)\tag{4}
とすれば、$x$を1次元、$z\in\mathbb{R}$として、
φ(x)=A\ \mathrm{exp}\left(-B(x-z)^2\right)\tag{5}\\
の時、
\begin{eqnarray}
φ(x_i)\ φ(x_j)
&=&\int_{-\infty}^{\infty}φ_z(x_i)\ φ_z(x_j)dz\\
&=&A^2\sqrt{\frac{\pi}{2B}}\ \mathrm{exp}\left(-\frac{B}{2}(x_i-x_j)^2\right)\\
&=&α\ \mathrm{exp}\left(-β(x_i-x_j)^2\right)\ =\ k(x_i,x_j)\tag{6}
\end{eqnarray}
つまるところ、$n$個のパラメータ$w$を推定することが、$z\in\mathbb{R}$に当てはまる全て(無限個)の特徴量$φ(x)$に対する回帰を行なっていることと同等になる。
\begin{eqnarray}
f(x)&=&\sum_{m=1}^{\infty} α_m\ φ_m(x)\\
&=&\sum_{i=1}^n w_i\ φ(x_i)^Tφ(x)\\
&=&\sum_{i=1}^n w_i\ k(x_i, x) \tag{7}\\
\end{eqnarray}
で、ガウス過程を用いた回帰。
という事は、データ数に等しいパラメータ(次元)を計算すればいい。
準備:既知の$n_1$個の$X_1$に対応する既知の$Y_1$を用意する。
目的:既知の$n_2$個の$X_2$に対応する未知の$Y_2$の分布を推定する。
ステップ1:$Y_1$を($n$次元正規分布のうちの)$n_1$次元で近似して、カーネル関数のパラメータを推定する。
ステップ2:そのパラメータから$\mu_1$と$\Sigma_1$を推定する。
ステップ2:$\mu_1$と$\Sigma_1$とカーネル関数のパラメータを用いて、$\mu_2$と$\Sigma_2$を推定する。
ステップ3:$\mu_2$と$\Sigma_2$を用いて $X_2$に対応する$Y_2$の分布を推定する。
という流れですね。
ベイズの考え方では、このモデルをあらかじめ組んでおけば、全ての推定は一度に行えるハズです。
実装編はまたそのうち。