線形混合モデルの導入
{tidyr} nestしていこう。では、こんなグラフを書きました。

iris %>%
ggplot(aes(Sepal.Width, Petal.Length, color = Species))+
geom_point()+
geom_smooth(method = "lm", se = F)
これは、アヤメ(iris)3種をそれぞれ独立として、ガクの幅(Sepal.Width)と花弁の長さ(Petal.Length)の間に相関があるのか考えた、という回帰分析になります。これら3種に共通の相関傾向があり、かつ、それぞれの種に応じた効果も認められるのか、否か、を検証したい時はどうするのか。
こういう場合、種に共通した相関傾向を固定効果、そこからの種ごとの変動をランダム効果として取り扱います。このように階層化された相関関係を取り扱う回帰分析を混合モデルと呼びます。この場合は線形混合モデル(linerd mixed model)です。
詳しい解説はここでは省きます。隅田先生によるこのpdf資料がよくまとまっていました。
{tidyr} nestしていこう。の考え方をうまく使い、model_lmm_1などというオブジェクトが乱立する治安の悪いRコードを避け、スマートにやっちまいましょう。
ランダム効果をベイズ的に取り扱う場合については、別記事にしました。
モデルの準備
ランダム効果の適切な導入法を検討するため、モデル選択を行います。
ここでは、それぞれのモデルに応じた関数を作っておきます。
# 切片と傾きに共分散を仮定した種ごとのランダム効果
model1 <- function(data)
lmer(Petal.Length ~ Sepal.Width + (Sepal.Width|Species), data = data)
# 切片を固定効果のみにし、傾きにランダム効果を導入
model2 <- function(data)
lmer(Petal.Length ~ Sepal.Width + (0 + Sepal.Width|Species), data = data)
# 傾きを固定効果のみにし、切片にランダム効果を導入
model3 <- function(data)
lmer(Petal.Length ~ Sepal.Width + (1|Species), data = data)
# 傾きと切片にそれぞれ独立のランダム効果を導入
model4 <- function(data)
lmer(Petal.Length ~ Sepal.Width + (1|Species) + (0 + Sepal.Width|Species), data = data)
# null model
model5 <- function(data)
lmer(Petal.Length ~ 1 + (1|Species), data = data)
で、作ったモデリング関数を1つのlistにまとめておきます。
# listは要素に関数も取れる。
listed_lmer <- list(model1, model2, model3, model4, model5)
特にモデル1とモデル4の違いはこの記述だけだとわかりづらいかもしれません。
久保先生の解説などご参照ください。
モデルの当てはめ
nestを使った畳み込みの考え方を、上手く利用していきましょう。
同じdataが5個縦に並んだカラムを用意しておきます。
で、それぞれのdataにそれぞれのモデルをフィットさせる処理をmap2を使って書きます。
最後に、特徴量を抽出します。
library(tidyverse)
library(lme4)
dat <- iris %>%
nest %>%
bind_rows(., ., ., ., .) %>% # ← ここがダサいんだよな。
rownames_to_column("id_model") %>%
mutate(model = map2(data, listed_lmer, ~.y(.x))) %>% # それぞれ当てはめ
mutate(AIC = map_dbl(model, ~extractAIC(.) %>% .[[2]]), # AIC抽出
deviance = map_dbl(model, REMLcrit), # 逸脱度
dev_exp = 1 - deviance / deviance[5], # Deviance explained
fixef = map(model, fixef), # 固定効果
ranef = map(model, ranef), # ランダム効果
predict = map2(model, data, ~predict(.x, .y))) # 予測値
結果はこうなります。
> dat
# A tibble: 5 x 9
id_model data model AIC deviance dev_exp fixef ranef predict
<chr> <list> <list> <dbl> <dbl> <dbl> <list> <list> <list>
1 1 <data.frame [150 x~ <S4: lmerMo~ 172. 160. 0.159 <dbl [2~ <S3: ranef.~ <dbl [150~
2 2 <data.frame [150 x~ <S4: lmerMo~ 176. 169. 0.115 <dbl [2~ <S3: ranef.~ <dbl [150~
3 3 <data.frame [150 x~ <S4: lmerMo~ 178. 171. 0.103 <dbl [2~ <S3: ranef.~ <dbl [150~
4 4 <data.frame [150 x~ <S4: lmerMo~ 172. 162. 0.152 <dbl [2~ <S3: ranef.~ <dbl [150~
5 5 <data.frame [150 x~ <S4: lmerMo~ 199. 191. 0 <dbl [1~ <S3: ranef.~ <dbl [150~
モデル選択
AICを使うとモデル1が最小、モデル4が次点でした(tibbleの表示がザンネン過ぎる)。
> dat %>% select(id_model, AIC) %>% arrange(AIC)
# A tibble: 5 x 2
id_model AIC
<chr> <dbl>
1 1 172.
2 4 172.
3 2 176.
4 3 178.
5 5 199.
> dat$AIC[c(1, 4)]
[1] 171.6244 171.8220
この中では、モデル1が「良い」モデルであると言えそうです。ただし、モデルの導入によって説明される残差平方和の比率はそれほど大きくないので、イマイチな感じ。
> dat$dev_exp[1]
[1] 0.1587998
どうしても検定したければ、logics-of-blueの馬場さんによるこちらの資料がよくまとまっています。
そうですねぇ。
library(lmerTest)を実行してからもう一度datを計算し直した後、anovaでp値が求まります。
解釈には注意が必要です。
> dat$model[[1]] %>% anova
Type III Analysis of Variance Table with Satterthwaite's method
Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
Sepal.Width 0.76793 0.76793 1 2.0549 5.1704 0.1475
可視化
畳み込まれているdatから必要部分を取り出してplotします。
モデルごとの回帰直線の比較。

dat %>% select(id_model, data, predict) %>% unnest %>%
unite(tag, c(Species, id_model), sep = "_", remove = F) %>%
ggplot(aes(x = Sepal.Width))+
geom_point(aes(y = Petal.Length, shape = Species))+
geom_path(aes(y = predict, group = tag, color = id_model), size = 2, alpha = 0.6)+
theme_classic()+
theme(strip.background = element_rect(color = "white"))
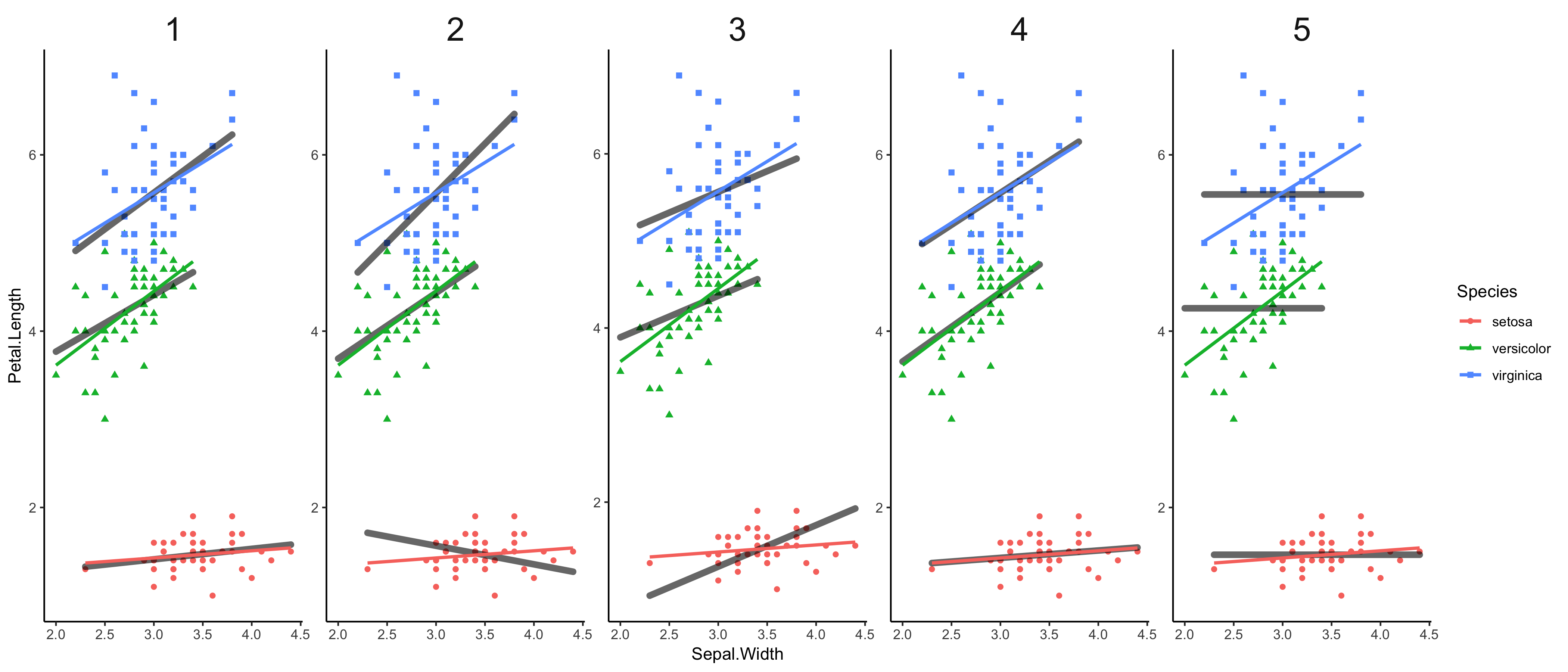
モデルごとの回帰直線と、種ごとに完全に独立に回帰した冒頭のグラフとの重ね合わせ。
dat %>% select(id_model, data, predict) %>% unnest %>%
unite(tag, c(Species, id_model), sep = "_", remove = F) %>%
ggplot(aes(x = Sepal.Width))+
geom_point(aes(y = Petal.Length, color = Species, shape = Species))+
geom_path(aes(y = predict, group = tag), size = 2, alpha = 0.6)+
geom_smooth(aes(y = Petal.Length, color = Species), method = "lm", se = F)+
theme_classic()+
theme(strip.background = element_rect(color = "white"),
strip.text = element_text(size = 21))+
facet_wrap(~id_model, scales = "free", nrow = 1)
ggplotってコードとして読みやすいのか、と言われるといつも悩みます。
修飾部分なしにすると大分マシです。探索的にはそれで十分。
修飾部分つけるとごちゃごちゃした見た目になって、慣れていないと読むのがツライものがあります。
ところで、datから必要部分を取り出してunnestする処理までを例えばdat_gなどと置いて、ggplotに入れるという書き方をずっとしていました。最近は、探索的にはインスタントなオブジェクトに戻らなくてもいいかなと思い直してパイプのままggplotに繋げるようにしました。そうするとggplotが更に読みづらくなってしまうので+で繋がる部分のインデントをもう一つ開けることにしました。今回はそのフォーマットです。
ん〜、多少、マシ、ですかね..。