Go to Qiita Advent Calendar 2024 Top
LoginSignup
2
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@kenji-kondo(近藤 憲児)

PythonでやるML Cycle1: Pythonに慣れる

Last updated at Posted at 2018-10-30

Pythonのインストールから実際にコードを書いてみるところまで。

ゴール

  • Pythonの開発環境を整備する。
  • Pythonのいくつかのライブラリを使ってちょっと数学的な事をコードで表現してみる。

Pythonの開発環境の構築してHello World!を出力する

説明

以下からPython(version 3.6.6)とIDEのPyCharmをインストールします。

注意として、

  • Pythonは2018/09現在最新の3.7.0をインストールしないよう注意。このバージョンではtensorflowがまだ対応していません。
  • PyCharmはProfessional版とCommunity版の二つがあります。どちらでもよいですが、Professional版はライセンス料がかかるので、まずは無料で、という人はCommunity版を選択しましょう。

PythonはJavaと比較してIDEがなくても書いてもいいかなという気持ちになりますが、やはりIDEを使いましょう。「インデントがなかった」といったしょーもないミスに時間を割きたくありません。

尚IDEであればPyCharmでなくてもOKです。Visual StudioでもPythonが書けるらしいので、例えばそれに慣れているならばそちらでも構いません。ただし以降はPyCharmを使っていることを前提に話を進めるため、VSを使用している場合は適宜補ってください。

上二つをインストールできたら、

を見て初期設定を行います。※PyCharmでpythonを動かす(Windows)のprint "Hello World!"はPython2のものなので、今回の環境(Python3)では動きませんのでご注意ください。

初期設定ができたらまずプロジェクトを作ります。

を参照してください。

手っ取り早くやりたいかたは

を参照してください。

最後に

を一通り眺めてください。

確認

プロジェクトを作成し、以下のコードを書いて、実行する。

print("Hello World!")

出力

Hello World!

Pythonの基本を知る

説明

まずデバッグによく使う対話型の実行環境Python Consoleを使ってみましょう。

PyCharmの左下にちっちゃく「Python Console」とあると思います。それをクリックするか、あるいは上段ツールバーの「Tools」からやはり「Python Console」を探してクリックします。すると以下のようなプロンプトが現れます。

PyDev console: starting.
Python 3.6.6 (v3.6.6:4cf1f54eb7, Jun 27 2018, 03:37:03) [MSC v.1900 64 bit (AMD64)] on win32

>>>

ここにコードを書いてEnterを押下すると、すぐに結果が現れます。

>>> print("Hello World!")
Hello World!

これから頻繁に使うので覚えておきましょう。

Pythonの基本文法ですが、ここでは説明しません。代わりに Progate のPythonに関するすべてのコースを受講してください。以下このコースの内容程度の理解を前提とします。

またPythonの文法に関することは、今後もあまり説明しないつもりです。辛いので。適宜Web上の記事や書籍を参照してください。必要な案内は可能な限りします。

完全なPython3(.6)の仕様は https://docs.python.org/3.6/ にあります。

機械学習でよく使われるライブラリを使ってみる

説明

まずnumpy, matplotlib, scipy, pandas のモジュールをインストールします。PyCharm(あるいはIntelliJ)でモジュールをインストールする方法は

を参照してください。

モジュールをインストールできたら、以下の記事から何ができるかを確認してください。

import matplotlib matplotlib.use('TkAgg')
import matplotlib.pyplot as plt

確認

    1. 以下の連立方程式を解く関数を作る。入力は$a$, $b$, $c$, $d$, それと $i$, $j$.
\left(
\begin{matrix}
a &b \\
c &d \\
\end{matrix}
\right)
\left(
\begin{matrix}
x_1 \\
x_2
\end{matrix}
\right)
=
\left(
\begin{matrix}
i \\
j
\end{matrix}
\right)

出力イメージ

>>> solve_2dim_equations(a=3, b=0, c=0, d=2, i=12, j=26)
array([ 4., 13.])
    1. 正規分布の密度関数のグラフを出力する。$\mu$と$\sigma$、定義域は適宜定数を当てはめてください。
f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left({- \frac{(x - \mu)^2}{2 {\sigma}^2}}\right).
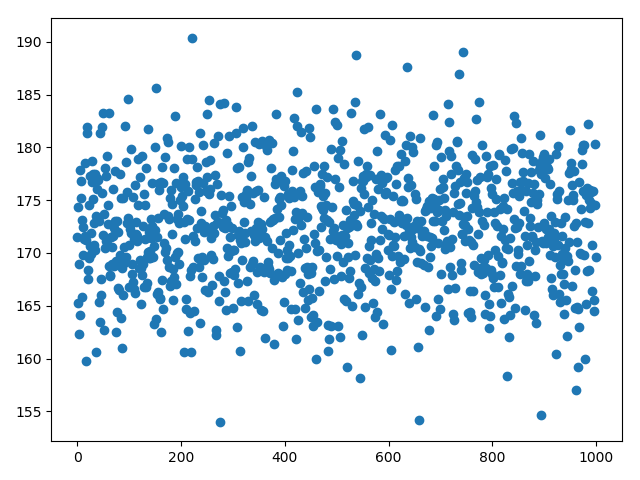
    1. 正規分布 $N(\mu = 172.14, \sigma^2 = 5.57^2)$ に従うサンプルデータを1,000個抽出して、それをCSVに出力してください。ちなみにこの分布は日本人男性30歳のもの。

出力イメージ

0,166.99038183853008
1,166.51281214908536
2,181.5585432128473
3,162.77441753222197
4,168.48261956594868
5,172.88492726845533
6,170.89622660999441
...
    1. 上で出力したCSVを読み込んで、散布図として描写してください。

イメージ

image.png

実践問題

1. ★サンプルデータを作る

Cycle2ではPRML(上)の序論、あるいは第3章にある線形回帰モデルを扱います。ここではそれに必要なサンプルデータを作ります。

$x \in$ { $ 0, , 0.01, , 0.02, , \dots, , 0.99 $ } の100個の入力データに対して、正規分布$N(\sin(2 \pi x), 0.3^2)$ に従うサンプルデータをそれぞれ抽出してください。それを以下二つの出力で表現してください。ただし、CSVに出力したデータは$x$を軸にランダムに並び替えてください:

  • CSVで出力
  • 散布図で出力

イメージ

CSV

0.9400000000000001,-0.878558954149004
0.14,0.3878279859542065
0.8200000000000001,-1.442692345490618
0.37,0.5459918361055303
0.56,-0.8708510248577344
0.33,0.6818388375590906
...

2. カオス理論入門

バタフライエフェクトという言葉をご存知でしょうか。バタフライエフェクトとは、「日本で蝶が羽ばたくと、アメリカでハリケーンが起こる」といった、ほんの小さな違いがのちの結果に大きな影響を与えること表す標語のようなものです。風が吹けば桶屋が儲かるですね。

実は数学の力学系理論という分野では、この現象について深く研究されています。

その中から、ロジスティック方程式と呼ばれる、生物の個体数の増減に関するモデルを使って、この現象を体験してみます。

ある地域に数百匹のウサギが生息しています。毎月ウサギの個体数を計測していたある調査員は、以下のことに気づきました:

  • 餌(植物)場の広さと餌の量から、その地域に生息できるウサギの個体数の上限は決まっている。
  • 個体数が上限よりも少ないときは、その地域に生えている餌が有り余っているので、個体数は月単位で増加する。
  • 一方、個体数が上限よりも多いときは、その地域の餌を食べつくしてしまって餓死するウサギが出てくるので、個体数は月単位で減少する。
  • さらにこの地域のウサギの天敵、つまり蛇やウサギを食用とする原住民が、毎月一定の割合でウサギを殺してしまうので、その分個体数は減少していく。

この現象を調査員が生態学者に伝えると、その生態学者は以下のような数学的モデルを立てました:

f(n + 1) - f(n) = f(n)(1 - f(n)) -h, \\

ここで$f(n)$は、$n$か月目に観測したときの、決まっている個体数の上限と実際に生息しているウサギの個体数の割合、$h$は天敵がウサギを殺す数と上限の割合を表しています。

$f(n) < 1$のときは餌が有り余っていて、$f(n) > 1$のときは餌が足りない状態です。$f(n)$は必ず0以上です。

$h = 1$のならば、ウサギの天敵がその地域で生息できるウサギの個体数の上限を1か月で殺してしまうことを意味しています。$h$が0に近いほど、天敵が1か月で殺すウサギの個体数が少ないことを意味しています。$h$もまた必ず0以上です。

以上のような条件で、$h$の値を0から1の間で色々と変えたときの、10年後(=120か月後)のウサギの個体数の割合$f(120)$をシミュレーションしてください。尚、初期値は$f(0) = 1$とします。

2
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?