
Shadertoy: Almost physically based glass

Shadertoy: Gem clock

Shadertoy: glass and metal hearts
この記事は WebGL Advent Calendar 2017 の8日目の記事です。
TL;DR
- 軽率なブルーオーシャン戦略で透過物体のリアルタイムレイトレースに手を出したものの、沼った話。
- いつもより技術的な話は少なめ。
- 多分、これを読んでも直接的な技術向上にはつながりません。
透過、いいよね
ガラス・水晶・宝石、古来より透過物体には人を惹きつける何かがあります。
実際、レイトレーシングやポリゴンレンダリングでは、透過物体の描画はとても人気があります。しかしシェーダアートの世界ではあまり見かけません。みんな大好き Shadertoy で、"refract", "glass", "crystal", "jewel", "diamond" などのキーワードで検索をかけて調べた事がありますが、5年間運営されているサービスにも関わらず、全 20000 作品中 200 作品程度しか見つけられませんでした。
世界中の変態コーダがよってたかって散々やりつくした感のある shadertoy に新規参入するにあたり、丁度いいチャレンジだと思いました。
皆がやらないワケがある
シェーダアートで透過物質が少ない理由は、計算負荷が高い・計算方法がシェーダプログラムに不向き、という2点にあります。
古典的なレイトレースでは、完全拡散反射(ランバート反射)面からは0本、鏡面反射面から1本、透過面から2本のレイを生成します(下図)。透過面でレイが2本に分裂するという事は、たった1つの透過物体を突き抜ける(透過面を2回通る)だけで計7回(1+2+4本)のレイトレースが必要になります。全反射条件もあるため、計算はより複雑です。
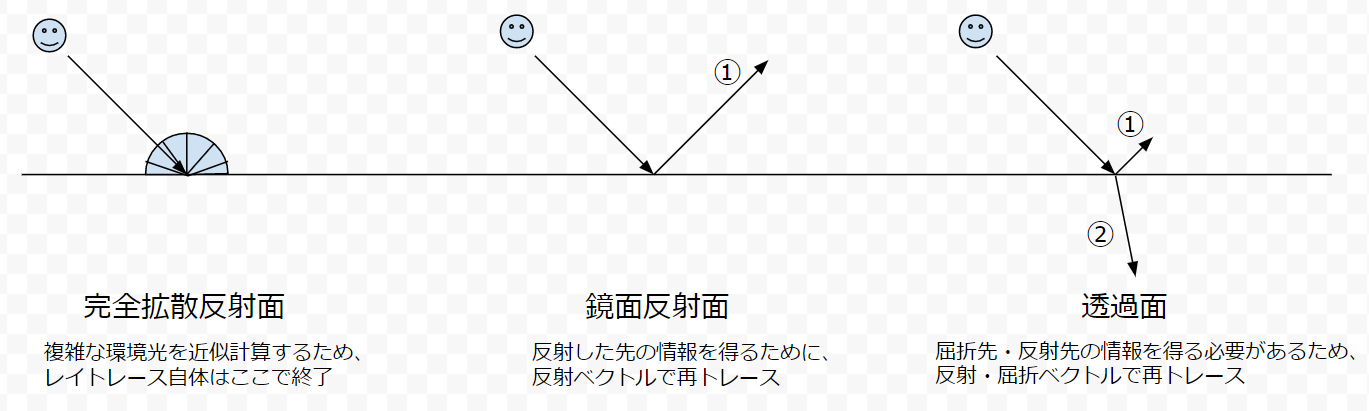
また、2本に分裂するレイトレースを実装する場合、通常は以下のように多重再帰を利用しますが、シェーダプログラムでは再帰呼び出しを使えません。このため、ちゃんとレイトレースするには、スタック領域を用意してループで多重再帰を再現する必要があります。
// 反射(reflect)と屈折(refract)をトレースする場合、多重再帰を利用すると簡単
vec4 ray_trace(in Ray ray, in int stackIndex) {
// MAX_STACK 以上の再帰計算は行わない
if (stackIndex > MAX_STACK) return background(ray);
// 反射レイ rayReflect(ray) と 屈折レイ rayRefract(ray) を計算して、自分(ray_trace)を呼び出す。
return ray_trace(rayReflect(ray), stackIndex+1) + ray_trace(rayRefract(ray), stackIndex+1);
}
先ほど、Shadertoyに200本作品程度の透過物体シェーダアートがあると書きましたが、実はその半分は屈折光しかトレースしていません。ちゃんと屈折・反射の両方をレンダリングしている作品はさらに少なくなります(ただし、全反射が多いダイヤモンドや、表面に細かい凸凹がある物などは、屈折だけでも十分な見た目になります。要は適材適所です)。
とりあえず実装(ちゃんとマルチパス)
実装が面倒くさいとはいえ、所詮は古典的レイトレースであり、光線追跡の計算に Ray Marching を利用するだけなので、まあできないことはないだろう。くらいの気持ちで実装を開始しました。以下、概念的なコードを示します。
// 反射と屈折を規定された回数分繰り返しトレースする
vec4 render(in Ray currentRay) {
vec3 col = vec3(0); // 出力
Hit hits[STACK_MAX]; // ヒット情報のスタック領域
int stackIndex = 1; // 情報を記録する位置のインデックス
int curretIndex; // レンダリングする位置のインデックス
// まず、普通にレイトレースして0番スタックに結果を代入
hits[0] = trace(currentRay);
// 各スタックを順次計算していく
for (curretIndex = 0; curretIndex < STACK_MAX; curretIndex++) {
// 情報を記録する位置を超えたら、レンダリング終了
// (GLSLではループ条件に変数を使えないため、ループ回数を変更するような場合は break を用いる)
if (curretIndex >= stackIndex) break;
// 表面ヒット情報を元に拡散反射色成分を計算し、出力情報に加算
col += diffusion(hits[curretIndex]);
// ヒットした表面が拡散反射面なら、トレース終了
if (hits[curretIndex].isDiffusionOnly) continue;
if (stackIndex < STACK_MAX-2) {
// スタックに余裕があれば次のトレース
hits[stackIndex] = trace(rayReflect(hits[curretIndex].ray)); // 反射を再トレースし、結果をスタックに代入
hits[stackIndex+1] = trace(rayRefract(hits[curretIndex].ray)); // 屈折を再トレースし、結果をスタックに代入
stackIndex = stackIndex + 2; // 情報を記録する位置を進める
} else {
// スタックに余裕が無ければトレースしない
// (単にトレースしないと黒くなってしまうので、暫定的に背景を描画)
col += background(hits[currentStack]);
}
}
// 演算結果を返す
return col;
}
しかし、動かない
表示が遅いどころか、表示される前にクラッシュして落ちる。

とりあえず、控えめに16個くらいのスタック領域でトレースしてみるかなー♪ →Crashed!
おいおい、うそやろ!?じゃあ、8スタックならどや?→Crashed!
えー。じゃあ、何スタックなら通んねん…→6個でCrashed! 5個ならOK。
...
心折れるわー
どういうことなの???
Shadertoyのスクリプトを読むと、このメッセージは WebGLContextLost イベントで表示されるようになっています。しかし MDN のリファレンスには「WebGLRenderingContext がロストすると発行されるよ」としか書いてありません。何かしらGPUで異常が発生すると起きるという事のようです。
GLSLのコンパイルはGPU内部で行われ命令セットなどは非公開のため、深く考えてもしょうがありません。とりあえずざっくり「コンパイルに一定時間以上かかったから強制終了された?or 許容命令数を超えた?」という可能性を基に簡略化することにしました。
(尚、作品アップロード後、inigo quilez 先生から**「WebGL2.0ではテクスチャの Level of Detail をきっちり指定せなアカンよ」**との指摘をいただき、比較的まともに動くようになりました。それでも重いですが。)
疑似的マルチパス
視覚的に重要度の低いトレースは間引いてしまえ、という戦略です。
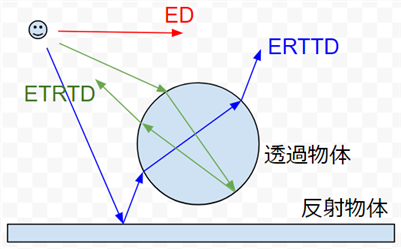
カメラ(E)、透過(T)、反射(R)、拡散(D)と定義した場合、古典的なレイトレースでは、必ずカメラ(E)から始まり、0回又は数回の透過(T)・反射(R)を経由して、最後は拡散面(または背景)で終わります(下図)。このパスの組み合わせは無数に存在しますが、そのうち実際に視覚的に重要度の高いパスを選択してレンダリングすれば、少ないトレースでも効率良くレンダリングできるはずです。
例えば、高屈折ガラス表面に45度から入ったレイは透過:反射=約9:1で分光します。反射が占める割合は視覚情報の10%程度ですが、2回透過した物体の奥の風景は視覚情報の90% x 90% = 81%になります。この場合、透過した先の風景の方が反射風景の方が優先度が高いと考える事ができます(実際は、フレネル反射のため反射情報も重要)。
実装方法
どうせ、数本のレイトレースしかできない事が判りましたので、開き直って、全展開してレンダリング結果への影響度の低いパスを手作業で消していきます。
まず、ループを実直に展開。
// 反射と屈折を規定された回数分繰り返しトレースする
vec4 render(in Ray currentRay) {
vec3 col = vec3(0); // 出力
Hit hits[STACK_MAX]; // ヒット情報のスタック領域
// まず、普通にレイトレースして0番スタックに結果を代入
hits[0] = trace(currentRay);
// 3段のマルチパス・レイトレースを全展開
col += diffusion(hits[0]);
if (!hits[0].isDiffusionOnly) {
hits[1] = trace(rayReflect(hits[0].ray)); // 1段目反射
col += diffusion(hits[1]);
if (!hits[1].isDiffusionOnly) {
hits[2] = trace(rayReflect(hits[1].ray)); // 2段目反射
col += diffusion(hits[2]);
if (!hits[2].isDiffusionOnly) {
hits[3] = trace(rayReflect(hits[2].ray)); // 3段目反射
col += diffusion(hits[3]);
hits[3] = trace(rayRefract(hits[2].ray)); // 3段目屈折
col += diffusion(hits[3]);
}
hits[2] = trace(rayRefract(hits[1].ray)); // 2段目屈折
col += diffusion(hits[2]);
if (!hits[2].isDiffusionOnly) {
hits[3] = trace(rayReflect(hits[2].ray)); // 3段目反射
col += diffusion(hits[3]);
hits[3] = trace(rayRefract(hits[2].ray)); // 3段目屈折
col += diffusion(hits[3]);
}
}
hits[1] = trace(rayRefract(hits[0].ray)); // 1段目屈折
col += diffusion(hits[1]);
if (!hits[1].isDiffusionOnly) {
hits[2] = trace(rayReflect(hits[1].ray)); // 2段目反射
//...(上の展開と同じなので以下略)...
}
}
// 演算結果を返す
return col;
}
...あまりに酷いので、マクロにまとめます。
# define REFLECT(i) hits[i] = trace(rayReflect(hits[i-1].ray)); col += diffusion(hits[i]);
# define REFRACT(i) hits[i] = trace(rayRefract(hits[i-1].ray)); col += diffusion(hits[i]);
vec4 render(in Ray currentRay) {
// ...(略)...
hits[0] = trace(currentRay);
col += diffusion(hits[0]);
if (!hits[0].isDiffusionOnly) {
REFLECT(1) // 1段目反射
if (!hits[1].isDiffusionOnly) {
REFLECT(2) // 2段目反射
if (!hits[2].isDiffusionOnly) {
REFLECT(3) // 3段目反射
REFRACT(3) // 3段目屈折
}
REFRACT(2) // 2段目屈折
if (!hits[2].isDiffusionOnly) {
REFLECT(3) // 3段目反射
REFRACT(3) // 3段目屈折
}
// ...(略)...
}
// 演算結果を返す
return col;
}
後はレンダリング結果を見ながら、間引くパスをコメントアウトすればOKです。
実装を見たい場合は、Shadertoy: Almost physically based glass のBufferAの202行目以降を参考してください(効率化のため連続する反射・屈折をひとまとめにトレースするマクロも組んでます)。
実験
実際にパスを少しづつ追加してレンダリングした結果です。
EDのみ

拡散光のみ計算した結果です。ガラスっぽさを出すために、物体表面に少し拡散光成分を入れているため、ほんのり色がついてます。
ERD追加

反射1回だけ追加。物体と床に映り込みが入りますが透過はしていません。ただ、フレネル反射を計算してるので不透明ガラスのような質感に。もうこれで良くない?
ETTD追加

透過2回のパスを追加。ETDというパスは、ガラス内に拡散反射する物体が埋め込まれてないとあり得ないので、このシーンでは意味がありません(追加しても変化なし)。また、2回しか透過出来ないため、物体奥の物体は不透明になってしまっています。
ERTTD追加

1回反射後に透過2回のパス。少しわかりにくいですが、ETTDだけでは床面に反射した物体が不透明です。この部分をちゃんとレンダリングさせています。
ETTTTD追加

透過4回のパスを追加。無事、物体奥の物体も透過しました。実際には ETTTTD の計算過程で ETTD、ETTTD の計算ができるので、これらのパスも含まれています。また、今回のコードでは、屈折計算で全反射も扱っているので、物体内で全反射している部分の精度も上がっている様子が分かります。
完成...
この時点で、実際に計算しているパスは ETTTTD と ERTTD ですので(他のパスはこの二つのどちらかに内包されている)、合計8回のレイトレース(下図、矢印の本数)でレンダリングしたイメージになります。
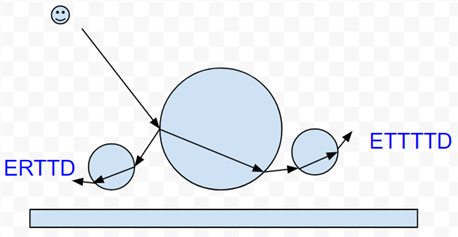
実際には、Level of Detail 指定によってクラッシュしにくくなったため、もう少し余裕がありますが(Almost physically based glass では8回透過と反射後4回透過まで計算してます)、シーン内に配置できる物体は複雑な形状2つと単純な形状1つで限界、もう一つ物体を追加するとクラッシュという感じです。最初の三つのシェーダアートでもこれ以上の物体は追加してません。
シーン内の形状を定義する距離関数はループ内で大量に展開されるため、ほんの少しの変更でも影響が大きいと思われます。
まとめ
本記事では、透過物質レイトレースの概念的な部分とクラッシュの回避について書きました。
ほとんど触れませんでしたが、媒質内の光の減衰の近似、フレネル反射の導入、透明物の影、トレースしきれなかった場所のレンダリング、鏡面反射物体との共存など、まだいろいろな技術要素があります。これらは、追ってちゃんとした技術記事として書ければと思います。
随分あっさりと沼から脱出したように見えるかもしれませんが、背後には相当数の試行錯誤が存在しています(特にWebGLのクラッシュについては、WebGL1.0だと動くのに2.0だと動かないとか謎な挙動が多い上に情報が極端に少なくて、かなり心が折れそうになりました)。ブルーオーシャンには大概青いなりの理由があるという事ですね。
ただ、この手のレンダリングエンジンは一度でも苦労して作ってしまえば、使いまわしが効きます。3種類程度しか物体を扱えないという制約はありますが汎用性は高いので、ぜひ自分のシェーダアートに組み込んでみて下さい。リアルタイムにレンダリングされる透明物体は、やはり感動的です。