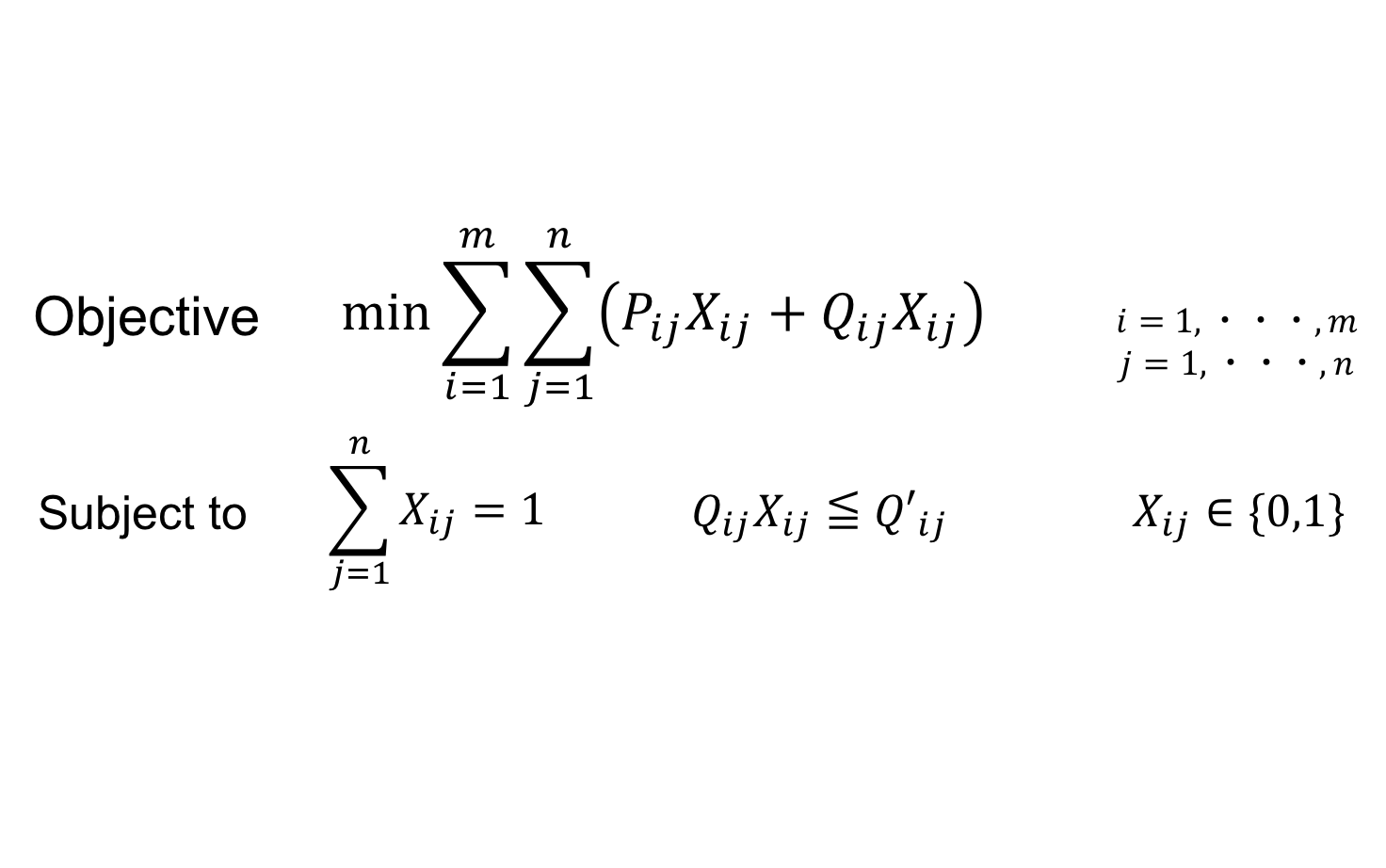LoginSignup
13
8

More than 3 years have passed since last update.

NTTドコモ 先進技術研究所Advent Calendar 2019Day 25
@keiichi_ochiai(Keiichi Ochiai)inNTTドコモ R&D

KDDCUP2019で1位を獲得した研究提案の紹介と採択されるまで

Last updated at Posted at 2019-12-24

ドコモの落合です。この記事では，KDD2019で開催されたデータ分析のコンペティションであるKDD Cupの1部門で優勝した1取り組みについて紹介します。

KDD Cup 2019概要

KDDの概要は前回の記事で紹介したので，ここではKDD Cupにフォーカスして説明します。KDD CupはKDDに併設されたデータサイエンスのコンペティションで初回は1997年と20年以上の伝統があります。昨年まではKaggleなどの通常のコンペティションと同様に，データと課題が与えられ，何らかの予測を行い，その精度を競うというコンペでした。これまでもドコモR&DではKDD Cupに挑戦しており，2016年に初挑戦しファイナリストになったことがありました。
　KDD Cup 2019では，従来の予測精度を競うコンペはRegular ML TrackのTask1として継続し，それ以外にも与えられたデータを使って自由に課題設定して研究提案するRegular ML Track Task2，機械学習の各工程（特徴抽出や予測モデル構築，検証など）を自動で行うAutoML Track，強化学習でマラリア感染の拡大を防ぐ方策を競うHumanity RL Trackが新設されました。ドコモでは全トラックに参加しており，Regular ML Track Task2で1位を獲得することができました。
https://www.kdd.org/kdd2019/docs/Winners_Regular_Baidu.pdf

Proposal Title: Simulating the Effects of Eco-Friendly Transportation Selections for Air Pollution Reduction
Keiichi Ochiai, Tsukasa Demizu, Shin Ishiguro, Shohei Maruyama, Akihiro Kawana
研究紹介ムービー：https://www.powtoon.com/online-presentation/bugFjP07kIK/eco-friendly-transportation-selections

Regular ML Trackの詳細

Regular ML Trackは中国のBaiduが主催し，Baidu Mapsの乗り換え検索ログが提供されました。ログは4種類ありますが，ここではTask2で利用した3種類だけ説明します。

提供されたログの説明

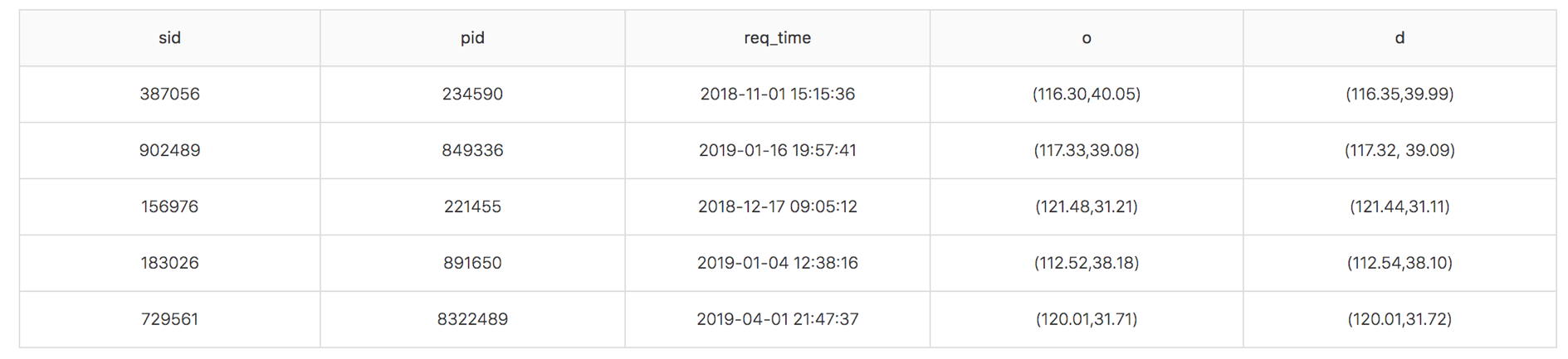
検索クエリログ（公式ページより引用）

検索クエリ

検索クエリのログは，sidがsession ID, pidがユーザID（実際はプライバシー保護のためある程度似たプロファイルの人で丸めている），req_timeが検索リクエストをした時刻，oが出発地の緯度経度，dが目的地の緯度経度です。

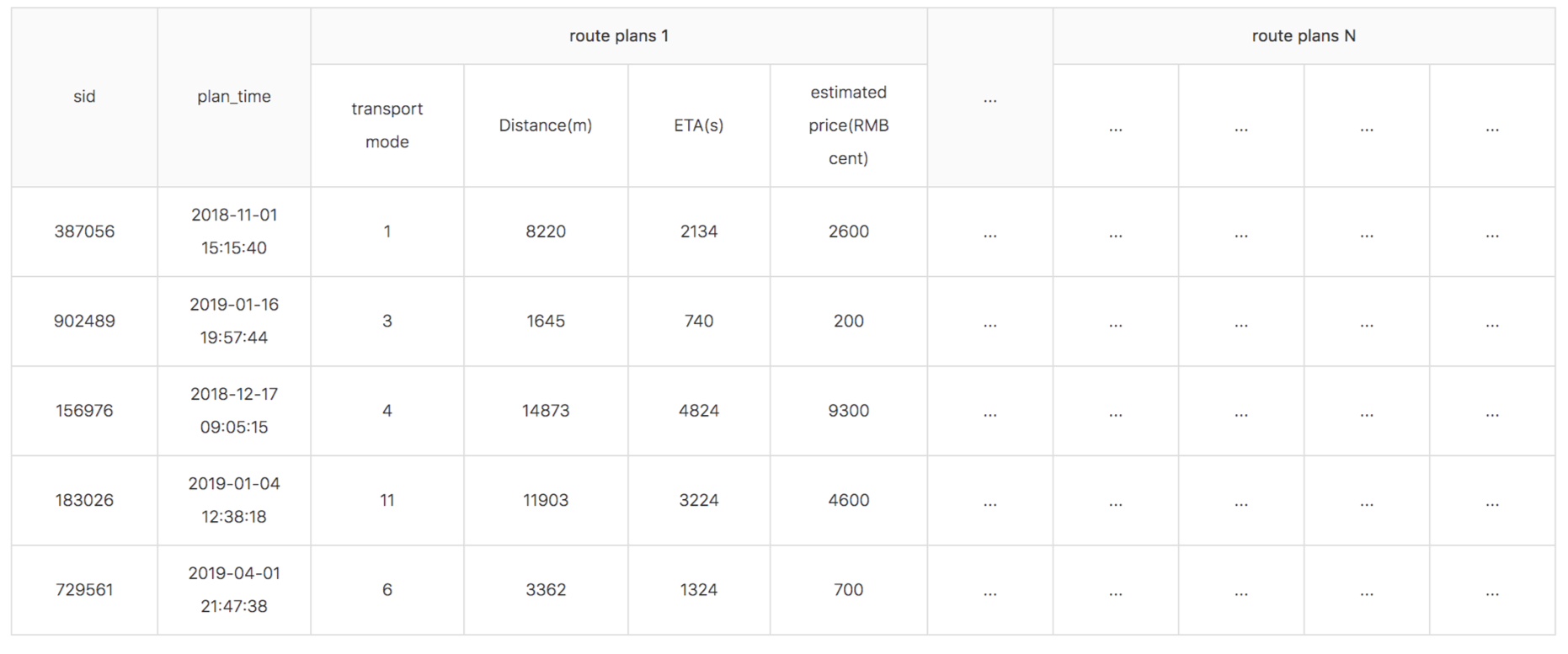
経路候補ログ

経路候補ログ

こちらも公式ページからの引用です。1つの検索クエリに対して，複数の経路（交通機関，交通モード）が提示されています。transport modeは交通機関を示すIDで，例えば1がバスで2が地下鉄で・・といった感じです。ただし，どのIDが実際のどの交通機関に対応しているかは公開されていませんでしたので様々な情報から推定しました。あとは，Distanceは距離，ETAは移動時間，estimated priceは利用料金です。このようなデータが1つのクエリに対して複数あります。

クリックログ

クリックログ

こちらも公式ページからの引用です。クリックログには，session IDと選択した交通モードが記録されています。sidをキーとして，ここまで述べた3つのログを紐づけることができます。

Regular ML Track Task1は，ここまで説明したログを元にユーザが利用する交通モードの予測を行うタスクでした。Task2は，上記のログを使って自由に課題設定を行い研究提案を行います。Task1は予測精度で評価できますが，Task2はそのような指標がないので，英語で4ページの論文を書いてCommittee memberが内容を評価するという通常の論文投稿のような形式で評価されました。

提案内容

私たちのチームでは，交通モードの選択と大気汚染の削減という環境問題を結びつけ提案を行いました。その詳細をここから説明していきます。

研究背景

環境問題は重要な社会問題の1つであり，CO2削減に向けた取り組みが世界規模で行われています。その一方，国連の発表によると2017年のCO2排出量が4年ぶりに増加に転じ，パリ協定の2℃目標（産業革命後の気温上昇を2℃以内に抑える）が難しいのではないかという意見もあります。

こうした状況を踏まえ，国や企業レベルの取り組みだけでなく個々人の取り組みも重要ではないかと考えています。個々人が環境問題に取り組む1つのアプローチとして，日々の生活で環境に優しい交通手段を選択するということが考えられます。しかしながら，単にCO2を排出する交通機関を利用しないようにするというのでは，人々にとって生活に支障が出るため，そのような行動は選択されないと考えられます。一方，生活に支障がない範囲であれば，CO2削減につながる交通手段を選択してもらえる可能性があります。交通手段を変えたときにどの程度CO2削減に貢献できるかわかった方が，ユーザーにとっても選択するモチベーションになると考えられます。しかし，効果を定量的に示すには人々の交通手段に関するログが必要になります。

そこで，この研究では，乗り換え検索サービスのログを使い，クリックした交通手段で実際に移動したと仮定することで，環境に優しい交通手段を選択した場合のCO2排出量の削減量のシミュレーションを行います。さらに，徒歩や自転車移動が増えることで健康にも良い影響があると考えられるので，健康への影響を定量的に評価します。

アプローチ

基本的なアイディア

あるユーザーに提示された経路候補ログから，各交通モードを利用したときのCO2排出量は以下の式で計算できます。

CO2排出量 = 移動距離(km)×単位距離・人あたりのCO2排出量(g/person・km)

移動距離は経路候補ログにあるので，単位距離・人あたりのCO2排出量がわかればCO2排出量が計算できます。そのデータは公益財団法人交通エコロジー・モビリティ財団が公開しているものがあり，それを利用します。例えば，BusとCyclingが経路候補の以下のログの場合，以下の赤枠のように計算できます。

CO2_calc.png

また，クリックログからこのユーザーがBusをクリックしていたことがわかります。ここで，代替の交通モードを受け入れ可能ということを以下のように定義します。

代替ルートの移動時間(ETA) ≦ クリックしたルートの移動時間
代替ルートのCO2排出量 < クリックしたルートのCO2排出量

1つ目の条件は移動時間が元々ユーザーが選択していた移動時間以下という条件です。環境に優しい交通モードは徒歩や自転車ですが，遠くまで歩くという候補が出ても選ばれないと考えられます。一方，元々選択していた交通モードの移動時間を超えなければ受け入れてもらえるだろうという想定です。2つ目の条件は，CO2排出量が減ることです。この受け入れ可能の定義に従うと，先ほど例ではCyclingが受け入れ可能となります。これを全検索ログに適用します。実際のログでは，数十万件の検索クエリに対して上記のような条件を満たす交通手段を探索するため，組合せ最適化問題 として定式化できます。

整数最適化問題としての定式化

交通モード選択を移動時間とCO2排出量の制約付きの0-1整数最適化問題として定式化します。最小化する目的関数と制約は以下のようになります。

定式化

ここで$P_{i,j}$はユーザー$i$が交通モード$j$を選択したときのCO2排出量，$Q_{i,j}$ はユーザー$i$が交通モード$j$を選択したときの移動時間， $Q\prime_{i,j}$はユーザー$i$がクリックした（実際に移動したと仮定した）交通モードの移動時間，$X_{i,j}$は選択した交通モードのみ1で他は0となるOne-hotベクトルのような値です。また，$m$はセッションID数，$n$は交通モード数を示します。実装の際にはCO2排出量と移動時間で単位が違うので両者を正規化しています。

最適化問題としての定式化には，大阪大学の梅谷先生のチュートリアルが非常に参考になりました。

組合せ最適化入門：線形計画から整数計画まで
https://www.slideshare.net/shunjiumetani/ss-17197023

定式化できれば，解くのは既存のソルバーを利用します。今回はPuLPというライブラリを使いました。

結果

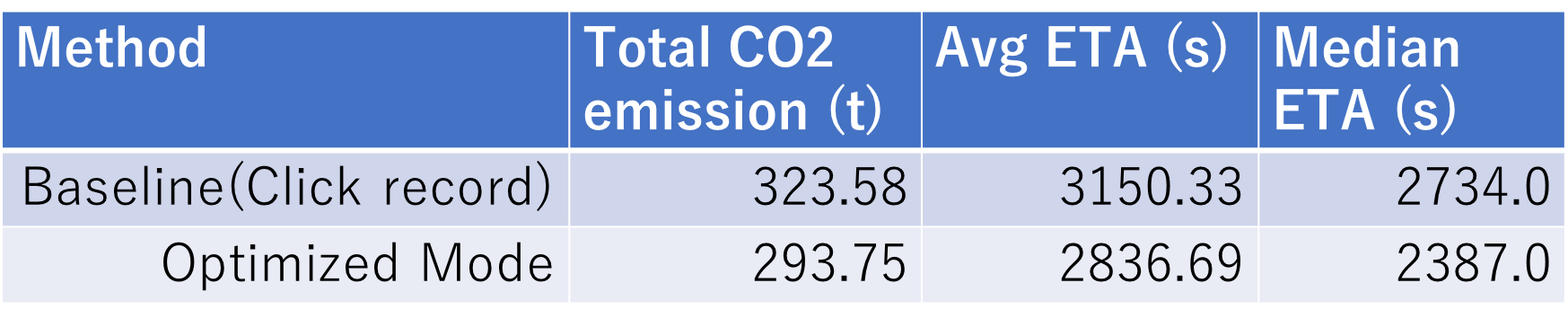
ユーザーのクリックログをベースラインとして，最適化後の結果と比較を行いました。結果は以下の表になります。約40万クエリの検索ログを対象に最適化を行いました。

結果

CO2排出量は約9.23%削減できるようです。意外にも移動時間も9.96%削減できるという結果になりました。ユーザーは必ずしも最速経路をクリックしているわけではないのかもしれません。

次に，最適化によって交通手段がどう変化したか見ていきます。下の表で括弧内の左がユーザーがクリックした交通モード，右が最適化で選択された交通モードです。

定性結果

公開されたログが北京中心部ということもあり，バスや地下鉄などで短距離を移動するケースが多かったようで，それを自転車に変えるという変更が多かったようです（表の赤枠）。一方，自家用車（Driving）では，自転車に変わっている件数が少なく自家用車のままが多いです（表の青枠）。車で移動するところは距離が遠く代替手段がないのかもしれません。

健康への影響については概要だけ説明します。Oxford大学の研究で，自転車に乗ることによる死亡率低下への影響を分析した研究があります（論文はこれ）。この研究によると，WHOが推奨している運動量（11.25 METh/weekの身体運動，150分の中程度の有酸素運動）をこなすと総死亡率が10%低下すると報告されています。今回のシミュレーションからユーザーは平均して1日あたり自転車に平均23.04分（WHO推奨の13.63%）乗ると計算できます。両者を組み合わせ，総死亡率を$10\% \times 13.63\% = 1.36\%$低下させる可能性があると考察しました。

交通手段の変化の結果を見てもわかりますが，今回の研究では自転車に置き換えられるところは自転車にするという結果になっています。しかし，実際にこれをやろうとすると駐輪スペースの問題があったり，天候によって受け入れられる交通手段が変わる（雨だったら自転車では移動したくない），どうやってユーザーにCO2が少ない交通手段を選んでもらうかというUI/UXなど，まだまだ実用までは課題があります。また，乗り換え検索でクリックした交通手段・ルートの通りに移動したと仮定していますが，実際にどうやって移動したのかわからないという根本的な制約もあります。

実装

最後に実装について少し紹介します。実装は以下の記事を参考にさせていただきました。
https://qiita.com/samuelladoco/items/703bf78ea66e8369c455
https://qiita.com/mzmttks/items/82ea3a51e4dbea8fbc17

事前にc_co2[i,j]にCO2排出量，c_eta[i,j]に移動時間（ユーザーi, 交通モードj）が入った辞書を作成しておきます。例えばこんな感じです。
c_eta[2,1] = 1976.0, c_eta[2,3] = 1146.0, c_eta[2,4] = 1446.0, c_eta[2,5] = 2246.0, c_eta[2,6] = 818.0
この例では，ユーザIDが2番のユーザーが交通モード1,3,4,5,6が候補として提示され，各交通モードでの移動時間が上記のようになっているとします。

import pulp
problem = pulp.LpProblem("ETA-CO2 minimize", pulp.LpMinimize)
x = {}

# 0-1変数を定義(制約条件3のX_{i,j}が0,1をの2値という制約に対応）
# define 0-1 variable
for i in I:
    for j in J:
        x[i,j] = pulp.LpVariable("x({:},{:})".format(i,j),  0, 1, pulp.LpBinary)

# 目的関数を定義。移動時間とCO2排出量をそれぞれ最大値で割って正規化します。
# define objective function. ETA and CO2 emission are normalized by dividing max
max_co2 = max(c_co2.values())
max_eta = max(c_eta.values())
problem += pulp.lpSum( ((c_co2[i,j]/max_co2) * x[i,j]) + ((c_eta[i,j]/max_eta) * x[i,j]) for i in I for j in J if (i,j) in c_co2), "TotalCost"

# 制約条件1: ユーザiについて、割り当ててよいモードは1つ
# constraint 1: each user can be assigned one mode
for i in I:
    problem += sum(x[i,j] for j in J if (i,j) in c_co2 ) == 1, "Constraint_leq_{:}".format(i)

# 制約条件2: ユーザiがクリックした交通モードの移動時間より短い
# click_log_dfにクリックログがpandasのdataframeとして入っている
# constraint 2: set "acceptable" condition
for n, t in click_log_df.iterrows():
    i = int(t["sid"])
    if (i,int(t["transport_mode"])) in c_co2:
        baseline = int(c_eta[i, int(t["transport_mode"])]*1.0)

    problem += sum(c_eta[i,j]*x[i,j] for j in J if (i,j) in c_co2 ) <= baseline, "Constraint_co2eq_{:}".format(i) 

# ソルバーを指定する
# set solver
solver = pulp.solvers.PULP_CBC_CMD()
result = problem.solve(solver)
# 最適化できたかどうかと，そのときの評価値を出力
# output
print(pulp.LpStatus[result], pulp.value(problem.objective))

タイムライン

KDD Cup 2019のRegular ML Trackは4/13頃に課題が公開されました。その後は以下のスケジュールで論文投稿まで行いました。

4/19　初回打ち合わせ（データ活用方法の案出し）
5/8　打ち合わせ#2（データ活用方法の案出し＆方針決定）
5/15　打ち合わせ#3（最適化のプログラムを実装、この時点では最適化が収束せず）
5/31　打ち合わせ#4（最適化実装完了）
6/3〜10　論文執筆（英語4ページ）
6/11〜12　英文校正
6/13　投稿
6/15　投稿締め切り（後日締め切り延長されて6月末までに）

2019年はゴールデンウィークに10連休があり，実質1ヶ月半程度で研究テーマ決め，実装，論文執筆まで行いました。

最後に

私自身は最適化問題には馴染みがなかったのですが，一緒に研究していた同僚が詳しく，定式化やPulpの実装，最適化がうまくいかないときの対応策について教えてくれました。また，別のメンバーが環境問題に応用しようという提案をしてくれたり，各交通モードがIDだけ提供されているところを，どのIDがどの交通モードなのかWebで公開されている運賃やデータの統計などを見ながら特定してくれたりとチームメンバーそれぞれが貢献してできた研究です。これからも面白い研究をして，学会発表などの対外活動を通じてドコモのデータ分析・AI分野の認知度を向上させたいと考えており，これからもKDDなどのトップカンファレンスに挑戦していきたいと思います。

それではみなさん，メリークリスマス&よいお年を！

  1. 世界最高峰のデータ分析競技会「KDD CUP 2019」で世界1位を受賞 https://www.nttdocomo.co.jp/binary/pdf/info/news_release/topics_190809_01.pdf ↩

13
8
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
13
8