追記(2023/06/05)
数理最適化ソルバー SCIP 専用の Python インターフェース PySCIPOpt の記事を書きました。
本追記時点で Python から SCIP を使用する方法としては、この PySCIPOpt がいちばんよいと思います。
追記(2022/11/08)
数理最適化ソルバーSCIP
ですが、
Since November 4, SCIP is licensed under the Apache 2.0 License.
となりました。SCIPは無償のソルバーの中では速いので、それが商用利用可能になったということは大きいです。Apache 2.0 Licenseなので、少なくともSCIPの内部コードを変更せず呼び出して使う場合は、作ったコードの開示義務(昔のことばでいうGPL汚染)はないはずです。
追記日時点では、PuLPからはSCIPが利用可能、Python-MIPからは不可能なようです。なので、しばらくはPuLPを使って記述し、SCIPを呼び出して解くのがよいと思うです。
やり方↓
ただ、コードを動かしたときに、動作手順としてはファイルベースのやりとり(PuLPが ~.mps という拡張子のファイルを出力 → SCIPが ~.mps ファイルを読み込んで計算 → 解をファイルに吐き出す(~.sol という拡張子だったかな?) → PuLPがファイルを読み込んで解に値を代入)となるので、扱う対象の変数の数・制約式の数がすごく多い場合は ~.mps ファイルが作られる部分で(本質的ではない)時間がかかる可能性があります。Python-MIPはファイルベースではなくライブラリ経由でソルバーとやりとりできるので、はやくPython-MIPがSCIP対応になるとよいですね。
なお、SciPyに数理最適化をしてくれる機能( scipy.optimize っていうんですか?)ができたそうですが、 整数線形(変数たちの中に整数の値しか取れないものが含まれ、かつ制約たちが全て線形式のもの)最適化問題 に関しては、PuLPを使って書いてソルバーにはSCIPを使用するほうがよいようです。あくまで感覚的な印象ですが、整数最適化問題を速く解く際のキーは分枝限定操作やヒューリスティックで良解を見つけることなので、連続最適化から発展した整数対応ソルバーよりも最初から変数に整数が含まれることを想定して設計されたソルバーのほうがスジがよいんですよね。
一例:https://mirucacule.hatenablog.com/entry/2022/08/06/190000
追記(2021/09/04)
PuLPはやめてPython-MIPを使いましょう。だれか解説記事書いて。
↓ keisukesato-acさんが書いてくれました
今度こそ?使い物になるフリーの数理最適化(混合整数最適化)ソルバー Python-MIP
追記(2020/05/25)
PuLPに同こんされておりデフォルトで使用される数理最適化ソルバー(1スレッド版COIN-CBC)は、(少なくともWindows版は)マルチスレッドに対応していないため、整数最適化問題を解くのに時間がかかることがあります。マルチスレッド版COIN-CBCへの置き換え方法を書いた記事があったので、リンクを貼ります。もちろん、無償で商用利用可能です。
- Windows: Python数理最適化パッケージPuLPの計算エンジンを速いものにする(Windows版お手軽編) & 計算時間を指定する
- Mac: 自分でインストールした CBCソルバをPuLPで使用する
追記(2020/05/11、2020/09/05)
※ MIPCLは入手性に難が出てきたので、あくまで無償の数理最適化ソルバーを使って数理最適化問題を速く解きたい場合は、まず↑にリンクを貼ったPuLP同こんのCOIN-CBCをマルチスレッド版に置き換えるほうをお勧めします。
「MIPCL」という別のフリーのソルバーのほうが、PuLP(に同こんされている1スレッド版COIN-CBC)よりも速く問題を解いてくれるようです。
(参考エントリー)
ついに使い物になるフリーの数理最適化ソルバーが登場? MIPCL
ただし、MIPCLはインストールや文法に少しクセがあるようなので、現在のところは、速さを求めるならMIPCL、手軽さを求めるならPuLP、という使い分けができるのではないかと思います。PuLPで書いて解くのに時間がかかったときにMIPCLに書き直すのも一つの手だと思います。
はじめに
数理最適化とか数理計画とか呼ばれる、こんな数学の問題
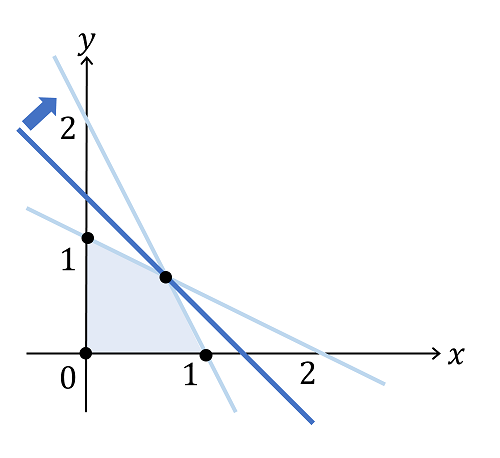
問題(1): 線形最適化問題(線形計画問題)
\begin{alignat}{2}
&\mbox{最大化}
&\qquad x + y & \\
&\mbox{制約}
& 2x + y &\leq 2 \\
&
& x + 2y &\leq 2 \\
&
& x &\geq 0 \\
&
& y &\geq 0 \\
\end{alignat}
や、こんな数学の問題
問題(2): 整数最適化問題(整数計画問題)
\begin{alignat}{3}
&\mbox{Minimize}
&\qquad \sum_{i \in I} \sum_{j \in J} c_{ij} x_{ij} &
&\qquad & \\
&\mbox{subject to}
& \sum_{j \in J} x_{ij} &\leq 1
& &\forall i \in I \\
&
&\sum_{i \in I} x_{ij} &= 1
& &\forall j \in J \\
&
& x_{ij} &\in \{0,1\}
& &\forall i \in I, \quad \forall j \in J
\end{alignat}
を解いてくれる、PythonのPuLPパッケージを紹介します。
対象ですが、目的関数と制約式が線形式(1次式)、変数が連続値または離散値またはそれらが混在したもので記述できるようなものとします。
余談ですが、問題(2)は、整数線形最適化問題(整数線形計画問題)と呼ばれることもあります。また、連続変数と離散変数が混在した問題は、混合整数最適化問題(混合整数計画問題、混合整数線形最適化問題、混合整数線形計画問題)と呼ばれます。
PuLPとは
PuLP自体は、Python上で数理最適化問題を簡単にコーディングできるモデリングAPI、モデリング言語だと思ったほうがよいです。実際に数式を解いてくれるソルバーとは別物なのですが、COINというソルバーが同こんされているので、PuLPをインストールするだけで問題を解けるようになります。PuLP自体はCOIN以外にもいくつかのソルバーに対応しているので、それらのソルバーが別途インストールされていれば、PuLPから呼び出すソルバーを(簡単に)切り替えることができます。
参考
先人たちのQiitaエントリー
本家サイト
- https://pypi.python.org/pypi/PuLP
- http://pythonhosted.org/PuLP/
- https://www.coin-or.org/ (同こんされているソルバーCOIN)
なぜPython+PuLPなのか
あくまで個人的な見解ですが…
お値段
Gurobi OptimizerとかIBM ILOG CPLEX Optimization StudioとかFICO Xpress Optimization SuiteとかNumerical Optimizerとかは高いし…
→ PuLPは無料!同こんされているソルバーCOINも無料!!
お速さ
GLPKやlp_solveは遅いし…Microsoft Excelは遅いうえに扱える変数や制約式の数も少ないし…
→ PuLPに同こんされているCOINはフリーのソルバーでは悪くないほう!ちょっとコードを変えるだけで商用ソルバーも呼べる!!
お商用利用
SCIPは商用利用したけりゃメールくださいって書いてあるし…
→ PuLP & COINは商用利用OK!組み込んだ製品のソースコードの公開義務もない!!
おモデル記述言語
C言語で有名なK&RのKさんが開発にかかわったというモデリング言語AMPLや、IBM ILOG CPLEX Optimization StudioとかFICO Xpress Optimization SuiteとかNumerical Optimizerとかにもある独自のモデリング言語、あれって数式みたいにモデルを記述できるからわかりやすいよね。でもほかじゃ使えないし、込み入ったことをやろうとするとマニュアルを見なきゃいけないし、ググっても情報少ないし…
→ PuLPも数式みたいにモデルを書ける!Pythonなのでほかのアルゴリズムとの連携も簡単だし、わからなくなったらググれば情報がたくさん!!モデル部分の記述はそのままにして呼び出すソルバーだけ変えられるので、実質PuLPが共通言語になり得る!!!
お開発環境
IBM ILOG CPLEX Optimization StudioとかFICO Xpress Optimization Suiteについてくる統合開発環境、いろいろ情報が表示できるしマウスでポチポチできて便利だよね。でもほかじゃ使えないし…
→ PythonなのでVisual Studio CodeやVisual Studio(タダであるCommunityエディションやExpressエディションでも)、Jupyter NotebookやSpyder上で使える!いろんなマシーンや環境で動く!!誰でもどこでも共同開発やテストができる!!!
研究者さんや学生さんへ
研究者さんや学生さんは、研究や学習を用途として、商用ソルバーが安価にあるいは無償で手に入るかもしれません。
研究者さんは、研究内容が将来的に商用実用化に向かうもののようでしたら、その際にかかるコストも考慮して、今のうちからPython+PuLPの使用を検討ください。何回も書いてますが、PuLPからコールするソルバーは簡単に切り替えられるので、商用ソルバーの深いところ(整数最適化のパラメーターのチューニングなど)まで触る必要がないなら、モデリングAPIとしてPuLPは十分だと思います。また、Python用APIを持つ商用ソルバーからの移植や両立についても、必要となるコーディング量はそれほど多くはなりません。
学生さんは、現在のバイト先あるいは将来の就職先やその客先などで数理最適化を活用することを考えて、今のうちからPython+PuLP(COIN)の使用を検討ください。もちろん案件の規模にもよりますが、商用ソルバーの購入や保守の費用を捻出させるだけの費用対効果を説明するのはけっこうハードル高いです。企業からの委託研究や共同研究などをしている場合でも同じです。企業の人が使える選択肢を考えてください。
以上、個人的な見解でした。
※ 最近でてきたフリーのソルバーMIPCLのことはよくわからないので、触れていません。すみません。
想定環境
以下、(サポート中の)WindowsでPython 3.7に対応したAnacondaの場合を想定して書きます。MacやLinuxなどでは適宜置き換えてください。
※ Python 2系(2.7など)は古いので使うのはやめましょう。
インストール
事前かくにん!
もし、自分でインストールしたPythonのほかに、過去にGurobi Optimizerやシミュレーションソフトなどをインストールしていたならば、Pythonの処理系がひっついてきている可能性があります。その場合は、コマンドプロンプト(Windowsのスタートボタン → Windowsシステムツール → コマンド プロンプト)を起動してwhere pythonやwhere pipと打って、どの処理系が優先されるか確認してみましょう。
もし、以下のように、Anaconda3フォルダーがいちばん先に表示されたら、この記事の想定どおり、Anacondaが優先されているということになります。
C:\Users\(ユーザー名)>where python
C:\Users\(ユーザー名)\Anaconda3\python.exe
C:\Users\(ユーザー名)\AppData\Local\Microsoft\WindowsApps\python.exe
C:\Users\(ユーザー名)>where pip
C:\Users\(ユーザー名)\Anaconda3\Scripts\pip.exe
C:\Users\(ユーザー名)>
もし、Anaconda3フォルダーではないものが先に表示されたら、Anacondaではない処理系が優先されているということになります。このままでよいかご自分で判断して、必要があれば「環境変数」の「Path」に記載されているものの順番を変更してください。
もし、以下のように表示されるか、ほかの処理系は表示されるもののAnaconda3フォルダーは表示されない場合は、
C:\Users\(ユーザー名)>where python
情報: 与えられたパターンのファイルが見つかりませんでした。
C:\Users\(ユーザー名)>
いわゆるAnacondaの「パスが通っていない」状態です。おそらく、Anacondaをインストールした際に、「Add Anaconda to my PATH environment variable」にチェックを入れなかったためと思われます。
(参考)https://weblabo.oscasierra.net/python-anaconda-install-windows/
その場合、(自力、あるいは、Anacondaをアンインストールし再インストールして)パスを通すか、コマンド プロンプトではなくAnaconda Prompt(Windowsのスタートボタン → Anaconda3 (64bit) → Anaconda Prompt)で以降の作業を行ってください。
よかった。 からの実作業
(環境変数の並び替えをした場合などは必要となるので、)念のため、いったんコマンドプロンプトを閉じて、また開きます。なお、Pythonが管理者権限での書き込みが必要なフォルダーにインストールされている場合(例えば、Anacondaのインストールで「All users (requires admin privileges)」を選択した場合)は、「管理者として実行」で起動します。
もし企業の内部などからインストールしようとしてプロキシーに邪魔される場合は、以下のようにして一時的にコマンドプロンプトにプロキシーを設定すればいけそうです(IPアドレスとポート番号はご自分の環境での数値に置き換えてください)。
set HTTP_PROXY=111.222.111.222:3333
set HTTPS_PROXY=111.222.111.222:3333
参考:http://d.hatena.ne.jp/showhey810/20140905/1409892787
pulpをダウンロードしてインストールするため、pip install pulpと打ちます。もしセキュリティーソフトが通信許可を求めてきたときは、許可をしてください。
うまくいった場合は、以下のように表示されるはずです。
C:\Users\(ユーザー名)>pip install pulp
Collecting pulp
Downloading PuLP-2.1-py3-none-any.whl (40.6 MB)
|■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■| 40.6 MB 6.4 MB/s
Requirement already satisfied: pyparsing>=2.0.1 in c:\users\(ユーザー名)\anaconda3\lib\site-packages (from pulp) (2.4.6)
Installing collected packages: pulp
Successfully installed pulp-2.1
C:\Users\(ユーザー名)>
すでにインストールされている場合は、以下のように表示されるはずです。すでにインストールされているので、問題はありません。
C:\Users\(ユーザー名)>pip install pulp
Requirement already satisfied: pulp in c:\users\(ユーザー名)\anaconda3\lib\site-packages (2.1)
Requirement already satisfied: pyparsing>=2.0.1 in c:\users\(ユーザー名)\anaconda3\lib\site-packages (from pulp) (2.4.6)
C:\Users\(ユーザー名)>
(メモ)
-
python -m pip install pulpでもインストールできます。 -
pip install -U pulpまたはpython -m pip install -U pulpでpulpのアップデートができます。
例(1)
冒頭の問題(1)を解きます。
\begin{alignat}{2}
&\mbox{最大化}
&\qquad x + y & \\
&\mbox{制約}
& 2x + y &\leq 2 \\
&
& x + 2y &\leq 2 \\
&
& x &\geq 0 \\
&
& y &\geq 0. \\
\end{alignat}
コード
# coding: UTF-8
# 線形/整数線形最適化問題を解くためにPuLPをインポート
import pulp
# sys.maxsizeでpythonで扱える整数(int)の最大値を取得するためにインポート
import sys
# 数理最適化問題(最大化)を宣言
problem = pulp.LpProblem("Problem-1", pulp.LpMaximize)
# 変数(連続)を宣言
# * 変数オブジェクトそのもの(x, y)と、
# 変数を文字列で表現したもの("xx", "yy")とを区別するため、
# あえて文字列表現のほうを"xx", "yy"と書いています
x = pulp.LpVariable("xx", 0, sys.maxsize, pulp.LpContinuous)
y = pulp.LpVariable("yy", 0, sys.maxsize, pulp.LpContinuous)
# 目的関数を宣言
# * かっこは不要だけど、わかりやすさのため記載
problem += ( x + y, "Objective" )
# 制約条件を宣言
problem += ( 2 * x + y <= 2 , "Constraint_1" )
problem += ( x + 2 * y <= 2 , "Constraint_2" )
# 問題の式全部を表示
# * 変数の文字列表現は、問題をprint文で表示したときに使用されます
print("問題の式")
print("-" * 8)
print(problem)
print("-" * 8)
# 計算
result_status = problem.solve()
# (解が得られていれば)目的関数値や解を表示
print("")
print("計算結果")
print("*" * 8)
print(f"最適性 = {pulp.LpStatus[result_status]}")
print(f"目的関数値 = {pulp.value(problem.objective)}")
print(f"解 x = {pulp.value(x)}")
print(f" y = {pulp.value(y)}")
print("*" * 8)
出力
問題の式
--------
Problem-1:
MAXIMIZE
1*xx + 1*yy + 0
SUBJECT TO
Constraint_1: 2 xx + yy <= 2
Constraint_2: xx + 2 yy <= 2
VARIABLES
xx <= 9.22337203685e+18 Continuous
yy <= 9.22337203685e+18 Continuous
--------
計算結果
********
最適性 = Optimal
目的関数値 = 1.33333334
解 x = 0.66666667
y = 0.66666667
********
余談(1)
演算子のオーバーロードが使える言語は、数理最適化の式をラクに記述できますね。そうでない言語は…Javaさんは……
例(2)
冒頭の問題(2)を解きます。
\begin{alignat}{3}
&\mbox{Minimize}
&\qquad \sum_{i \in I} \sum_{j \in J} c_{ij} x_{ij} &
&\qquad & \\
&\mbox{subject to}
& \sum_{j \in J} x_{ij} &\leq 1
& &\forall i \in I \\
&
&\sum_{i \in I} x_{ij} &= 1
& &\forall j \in J \\
&
& x_{ij} &\in \{0,1\}
& &\forall i \in I, \quad \forall j \in J.
\end{alignat}
余談(2)
数理最適化の式って、$\sum$を頻繁に使いますよね。数理最適化のモデリング言語は、$\sum$をどう記述できるかが使いやすさの基本になってきます。その点、PuLPは安心です。
ところで、数理最適化の入門テキストで、この問題でいうところの集合$I$や$J$を、$I:=\{1, \ldots, m\}$や$J:=\{1, \ldots, n\}$などと、むりやり1から番号づけして、例えば制約条件を
\sum_{j = 1}^{n} x_{ij} \leq 1 \quad \mbox{for} \;\; i = 1, \ldots, m
などと記述しているものがありますが、$I$や$J$の要素が何を表しているのか、数字の$2$は$I$と$J$のどっちの要素なのか、混乱してくるので、集合を正の整数の列に置き換えず、集合の要素の名前も元の名前のまま使うことをお勧めします。PuLPでは、Pythonの辞書やタプルといった言語仕様を使うことで、自然にモデリングできます。
あと、この問題の$\LaTeX$コマンドで書いた数式のように、各式の縦をそろえると、見やすくなっていいですよね。
あとあと、この問題は、0-1変数$x_{ij} \in \{0,1\}$を連続変数$0 \leq x_{ij} \leq 1$などに緩和(緩い条件に変更)して問題を解いても、問題の全ユニモジュラ性(total unimodularity)のおかげで整数の最適解が存在し、それを得ることができることがよく知られています。が、実際に仕事でモデル化すると、どんどん制約条件が増えていって、全ユニモジュラ性が成り立たなくなっちゃうのがほとんどなんですよね。
コード
# coding: UTF-8
# 線形/整数線形最適化問題を解くためにPuLPをインポート
import pulp
# 計算時間を計るのにtimeをインポート
import time
# 作業員の集合(便宜上、リストを用いる)
I = ["Aさん", "Bさん", "Cさん"]
print(f"作業員の集合 I = {I}")
# タスクの集合(便宜上、リストを用いる)
J = ["仕事イ", "仕事ロ", "仕事ハ"]
print(f"タスクの集合 J = {J}")
# 作業員 i を タスク j に割り当てたときのコストの集合(一時的なリスト)
cc = [
[ 1, 2, 3],
[ 4, 6, 8],
[10, 13, 16],
]
# cc はリストであり、添え字が数値なので、
# 辞書 c を定義し、例えばcc[0][0] は c["Aさん","仕事イ"] でアクセスできるようにする
c = {} # 空の辞書
for i in I:
for j in J:
c[i,j] = cc[I.index(i)][J.index(j)]
print("コスト c[i,j]: ")
for i in I:
for j in J:
print(f"c[{i},{j}] = {c[i,j]:2d}, ", end = "")
print("")
print("")
# 数理最適化問題(最小化)を宣言
problem = pulp.LpProblem("Problem-2", pulp.LpMinimize)
# pulp.LpMinimize : 最小化
# pulp.LpMaximize : 最大化
# 変数集合を表す辞書
x = {} # 空の辞書
# x[i,j] または x[(i,j)] で、(i,j) というタプルをキーにしてバリューを読み書き
# 0-1変数を宣言
for i in I:
for j in J:
x[i,j] = pulp.LpVariable(f"x({i},{j})", 0, 1, pulp.LpInteger)
# 変数ラベルに '[' や ']' や '-' を入れても、なぜか '_' に変わる…?
# lowBound, upBound を指定しないと、それぞれ -無限大, +無限大 になる
# 内包表記も使える
# x_suffixes = [(i,j) for i in I for j in J]
# x = pulp.LpVariable.dicts("x", x_suffixes, cat = pulp.LpBinary)
# pulp.LpContinuous : 連続変数
# pulp.LpInteger : 整数変数
# pulp.LpBinary : 0-1変数
# 目的関数を宣言
problem += pulp.lpSum(c[i,j] * x[i,j] for i in I for j in J), "TotalCost"
# problem += sum(c[i,j] * x[i,j] for i in I for j in J)
# としてもOK
# 制約条件を宣言
# 各作業員 i について、割り当ててよいタスク数は1つ以下
for i in I:
problem += sum(x[i,j] for j in J) <= 1, f"Constraint_leq_{i}"
# 制約条件ラベルに '[' や ']' や '-' を入れても、なぜか '_' に変わる…?
# 各タスク j について、割り当てられる作業員数はちょうど1人
for j in J:
problem += sum(x[i,j] for i in I) == 1, f"Constraint_eq_{j}"
# 問題の式全部を表示
print("問題の式")
print(f"-" * 8)
print(problem)
print(f"-" * 8)
print("")
# 計算
# ソルバー指定
solver = pulp.PULP_CBC_CMD()
# pulp.PULP_CBC_CMD() : PuLP付属のCoin-CBC
# pulp.GUROBI_CMD() : Gurobiをコマンドラインから起動 (.lpファイルを一時生成)
# pulp.GUROBI() : Gurobiをライブラリーから起動 (ライブラリーの場所指定が必要)
# ほかにもいくつかのソルバーに対応
# (使用例)
# if pulp.GUROBI_CMD().available():
# solver = pulp.GUROBI_CMD()
# 時間計測開始
time_start = time.perf_counter()
result_status = problem.solve(solver)
# solve()の()内でソルバーを指定できる
# 何も指定しない場合は pulp.PULP_CBC_CMD()
# 時間計測終了
time_stop = time.perf_counter()
# (解が得られていれば)目的関数値や解を表示
print("計算結果")
print(f"*" * 8)
print(f"最適性 = {pulp.LpStatus[result_status]}, ", end="")
print(f"目的関数値 = {pulp.value(problem.objective)}, ", end="")
print(f"計算時間 = {time_stop - time_start:.3f} (秒)")
print("解 x[i,j]: ")
for i in I:
for j in J:
print(f"{x[i,j].name} = {x[i,j].value()}, ", end="")
print("")
print(f"*" * 8)
出力
作業員の集合 I = ['Aさん', 'Bさん', 'Cさん']
タスクの集合 J = ['仕事イ', '仕事ロ', '仕事ハ']
コスト c[i,j]:
c[Aさん,仕事イ] = 1, c[Aさん,仕事ロ] = 2, c[Aさん,仕事ハ] = 3,
c[Bさん,仕事イ] = 4, c[Bさん,仕事ロ] = 6, c[Bさん,仕事ハ] = 8,
c[Cさん,仕事イ] = 10, c[Cさん,仕事ロ] = 13, c[Cさん,仕事ハ] = 16,
問題の式
--------
Problem-2:
MINIMIZE
1*x(Aさん,仕事イ) + 3*x(Aさん,仕事ハ) + 2*x(Aさん,仕事ロ) + 4*x(Bさん,仕事イ) + 8*x(Bさん,仕事ハ) + 6*x(Bさん,仕事ロ) + 10*x(Cさん,仕事イ) + 16*x(Cさん,仕事ハ) + 13*x(Cさん,仕事ロ) + 0
SUBJECT TO
Constraint_leq_Aさん: x(Aさん,仕事イ) + x(Aさん,仕事ハ) + x(Aさん,仕事ロ) <= 1
Constraint_leq_Bさん: x(Bさん,仕事イ) + x(Bさん,仕事ハ) + x(Bさん,仕事ロ) <= 1
Constraint_leq_Cさん: x(Cさん,仕事イ) + x(Cさん,仕事ハ) + x(Cさん,仕事ロ) <= 1
Constraint_eq_仕事イ: x(Aさん,仕事イ) + x(Bさん,仕事イ) + x(Cさん,仕事イ) = 1
Constraint_eq_仕事ロ: x(Aさん,仕事ロ) + x(Bさん,仕事ロ) + x(Cさん,仕事ロ) = 1
Constraint_eq_仕事ハ: x(Aさん,仕事ハ) + x(Bさん,仕事ハ) + x(Cさん,仕事ハ) = 1
VARIABLES
0 <= x(Aさん,仕事イ) <= 1 Integer
0 <= x(Aさん,仕事ハ) <= 1 Integer
0 <= x(Aさん,仕事ロ) <= 1 Integer
0 <= x(Bさん,仕事ハ) <= 1 Integer
0 <= x(Bさん,仕事ロ) <= 1 Integer
0 <= x(Cさん,仕事イ) <= 1 Integer
0 <= x(Cさん,仕事ハ) <= 1 Integer
0 <= x(Cさん,仕事ロ) <= 1 Integer
--------
計算結果
********
最適性 = Optimal, 目的関数値 = 19.0, 計算時間 = 0.040 (秒)
解 x[i,j]:
x(Aさん,仕事イ) = 0.0, x(Aさん,仕事ロ) = 0.0, x(Aさん,仕事ハ) = 1.0,
x(Bさん,仕事イ) = 0.0, x(Bさん,仕事ロ) = 1.0, x(Bさん,仕事ハ) = 0.0,
x(Cさん,仕事イ) = 1.0, x(Cさん,仕事ロ) = 0.0, x(Cさん,仕事ハ) = 0.0,
********
おわりに
ボブの絵画教室よりも簡単だと思うので、ぜひPython+PuLPに触れてみてください。
解きたい問題の計算時間がかかる場合は、いちばん上にリンクを貼ったマルチスレッド版ソルバーの記事を見て、試してみてください。