機械学習の初心者がpythonで有馬記念を予想してみた

機械学習の初心者がpythonで...シリーズの第二弾です。

前回の記事『機械学習の初心者がpythonで競馬予測モデルを作ってみた』では、競馬を題材にして、簡単な学習モデルを構築する過程をまとめてみました。

今回は実践編ということで、2020年の総決算である有馬記念の予想を実際にしてみたいと思います。アドベントカレンダーの大トリを担当ということもあり、ちょうどタイミング的にもピッタリ？ですね！

※ 環境構築は前回の記事を参照してください

有馬記念とは？

中央競馬のGI競走の一つで、ファン投票によって出走馬が選出され、別名グランプリとも言われる1年を締めくくるビッグレースです。

レース概要はこちらです。

• 開催日：2020/12/27 (日)
• 競馬場：中山競馬場
• コース：芝2500m

小回りの中山競馬場の長距離レースということで、個人的には紛れが起きやすいレースだと感じています。実際に、3着以内に人気薄の馬が来ることも多く、予想しがいのあるレースとも言えます。

使用するデータセットの検討

前回は、過去5年分のデータを全て使用しました。今回は有馬記念を当てたい！と目的が明確なので、それに沿ったデータセットを検討します。

条件ごとにデータサンプル数をまとめたのがこちらです。
※ データの対象期間：2015年〜2020年(12/20まで)

条件	レース数	出走馬レコード数
全レース	20,677	293,120
中山競馬場の芝レース	1,276	18,109
中山競馬場の芝2000m以上のレース	479	6,621
中山競馬場の芝2500mのレース	58	711

今回は汎用的なモデルを作成するわけではなく、有馬記念の特徴に近いモデルを作成することに主眼を置きます。ただし、一定のサンプル数は必要なので、「中山競馬場の芝2000m以上のレース」のデータセットを使用することにしました。

データの前処理

前回と同様に、データの前処理を実施していきます。

最終的に以下のデータをpandasのDataFrameにロードしようと思います。

データ項目	用途	データ説明
race_index	index	開催されるレースを特定した識別ID
馬番号	説明変数	出走馬の馬番
レースクラス	説明変数	当該レースの階級を数値に変換(*1)
タイム指数	説明変数	出走馬の過去3レースのタイム指数(*2)の中央値
通過順4角	説明変数	出走馬の過去3レースの最終コーナー通過順の中央値
騎手名	説明変数	騎手名をダミー変数化して使用
種牡馬名	説明変数	種牡馬名をダミー変数化して使用
3着以内	目的変数	出走馬の着順を3着以内なら1、4着以下なら0に変換

(*1) レースクラスは以下のルールとします

レースクラス	変換した数値
新馬	250
未勝利	250
1勝クラス / 500万	500
2勝クラス / 1000万	1000
3勝クラス / 1600万	1500
OP	2000
G3	3000
G2	4500
G1	7000

(*2) タイム指数はデータの取得元より提供される過去レースの走破タイムを指数化したものです

ローデータ（CSVファイル）の構成

今回の元データはこちらのCSVファイル群です。

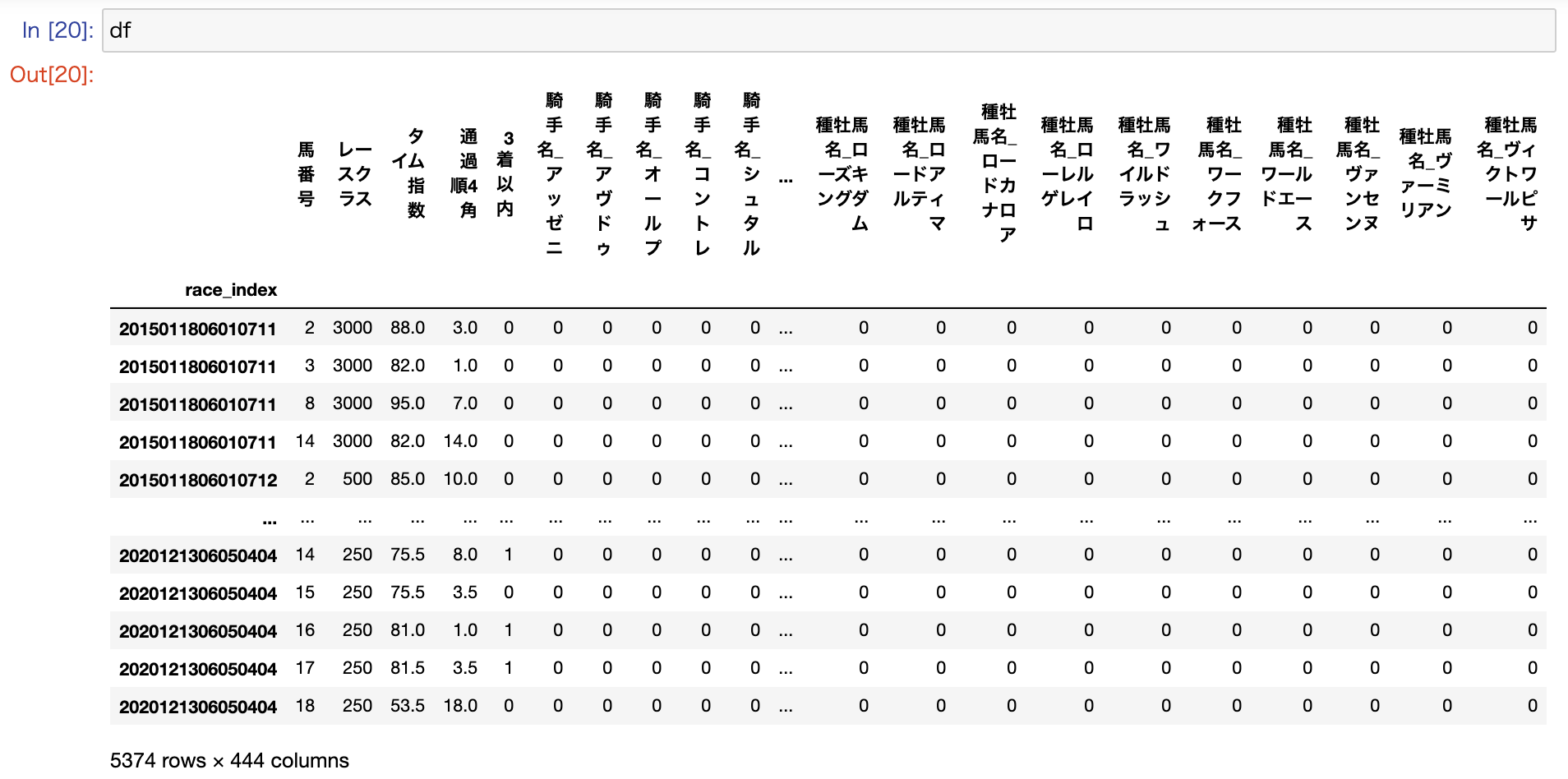
これらのデータをクレンジング・統合・変換して、以下のようにDataFrameにロードします。

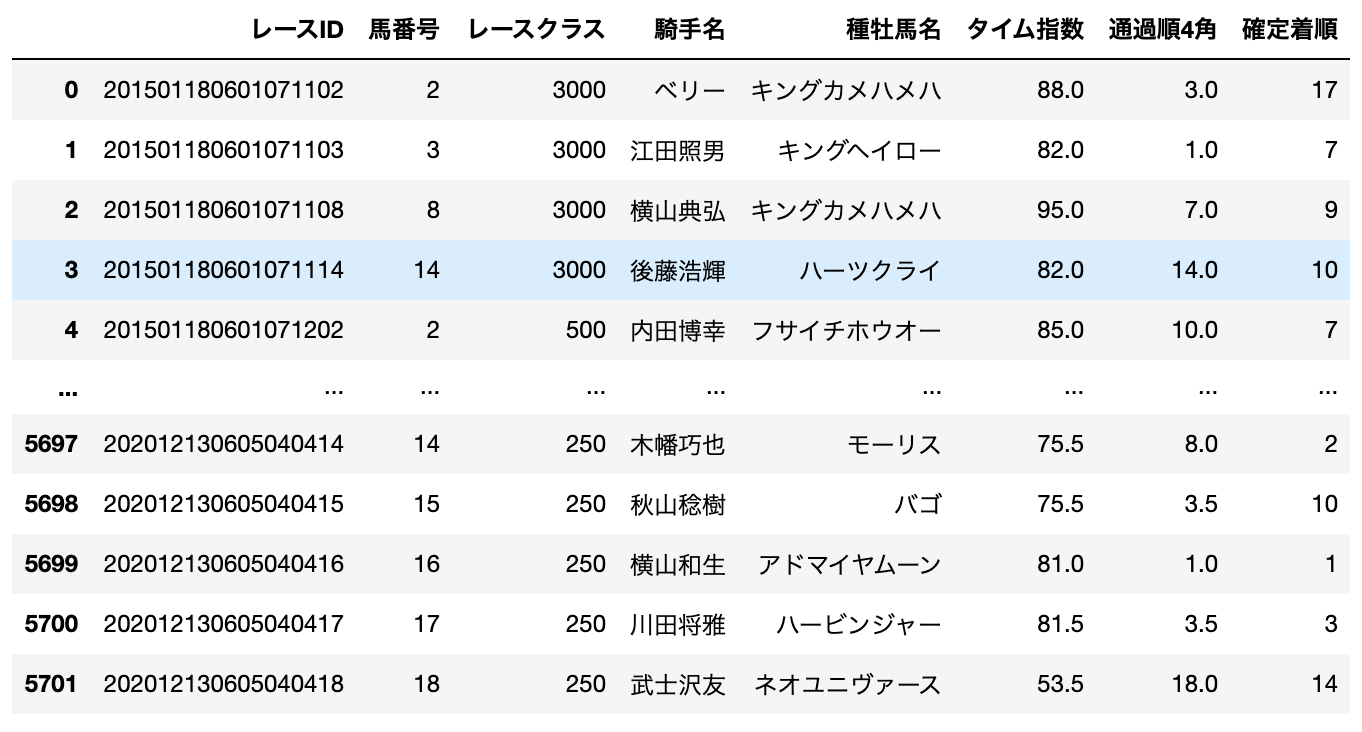
※ 実装部分は少々複雑だったので、ここでは割愛します

前処理の続き

それ以降は、前回と同じように、目的変数を生成したり、説明変数のダミー変数化などを順番に実施していきます。

sample.ipynb

(中略)

# 着順が3着以内かどうかのカラムを追加する
f_ranking = lambda x: 1 if x in [1, 2, 3] else 0
df['3着以内'] = df['確定着順'].map(f_ranking)

# ダミー変数を生成
df = pd.get_dummies(df, columns=['騎手名'])
df = pd.get_dummies(df, columns=['種牡馬名'])

# インデックスを設定（レースだけを特定する場合は、16バイト目までを使用）
df['race_index'] = df['レースID'].astype(str).str[0:16]
df.set_index('race_index', inplace=True)

# 不要なカラムを削除
df.drop(['レースID', '確定着順'], axis=1, inplace=True)

以上で、データの前処理が完了です。

モデルの学習と評価

続いて、モデルの学習をしていきますが、今回は前回使用したロジスティック回帰を含む以下の分類アルゴリズムを検証してみたいと思います。

アルゴリズム	概要
ロジスティック回帰	0〜1の確率で返される2択の予測結果を分類に使用する手法
サポートベクターマシン	クラスを最大に分ける境界線を引いて、分類する手法
K近傍法	予測対象データの近傍にあるデータ群の多数決で分類する手法
ランダムフォレスト	決定木(Yes/Noの分岐条件)を複数作って多数決で分類する手法

こちらの記事に分かりやすくまとまっています。
参考：機械学習の情報を手法を中心にざっくり整理

上記のアルゴリズムですが、全てsklearnに内包されており、それぞれの分類器クラスを作成する処理以外は、同様の実装で動作させることが可能です。

学習＆評価データ生成（共通処理）

前回と同様に以下の処理を実施していきます。

データ分割と標準化

データを説明変数と目的変数ごとに学習用データと評価用データに分割します。そして、今回は手間を省くために分割前の段階で説明変数を標準化しておきます。

sample.ipynb

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

# 説明変数をdataXに格納
dataX = df.drop(['3着以内'], axis=1)

# 目的変数をdataYに格納
dataY = df['3着以内']

# この段階で説明変数を標準化しておく
sc = StandardScaler()
dataX_std = pd.DataFrame(sc.fit_transform(dataX), columns=dataX.columns, index=dataX.index)

# データの分割を行う（学習用データ 0.8 評価用データ 0.2）
X_train, X_test, y_train, y_test = train_test_split(dataX_std, dataY, test_size=0.2, stratify=dataY)

変数名	データ種別	用途
X_train	説明変数	学習データ
X_test	説明変数	評価データ
y_train	目的変数	学習データ
y_test	目的変数	評価データ

データ不均衡を修正

sample.ipynb

from imblearn.under_sampling import RandomUnderSampler

# 学習データをアンダーサンプリング
f_count = y_train.value_counts()[1] * 2
t_count = y_train.value_counts()[1]
rus = RandomUnderSampler(sampling_strategy={0:f_count, 1:t_count})
X_train, y_train = rus.fit_sample(X_train, y_train)

※ 現バージョンのRandomUnderSamplerでアンダーサンプリングするとインデックス(race_index)が無くなってしまう問題が発生（大きな影響はないのでそのまま続行）

ロジスティック回帰による学習と評価

ここから、各アルゴリズムを使用したモデルの学習と評価を実施していきます。まずは、ロジスティック回帰からです。

sample.ipynb

from sklearn.linear_model import LogisticRegression

# 分類器を作成（ロジスティック回帰）
clf = LogisticRegression(max_iter=10000)

# 学習
clf.fit(X_train, y_train)

# 予測
y_pred = clf.predict(X_test)

# 正解率を表示
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_pred))
0.7488372093023256

# 適合率を表示
from sklearn.metrics import precision_score
print(precision_score(y_test, y_pred))
0.4158878504672897

# F値を表示
from sklearn.metrics import f1_score
print(f1_score(y_test, y_pred))
0.39732142857142855

サポートベクターマシン（SVM）による学習と評価

続いて、サポートベクターマシンを検証してみます。

sample.ipynb

from sklearn.svm import SVC

# 分類器を作成（サポートベクターマシン）
clf = SVC(kernel='rbf', gamma=0.1, probability=True)

# 学習
clf.fit(X_train, y_train)

# 予測
y_pred = clf.predict(X_test)

# 正解率を表示
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_pred))
0.7581395348837209

# 適合率を表示
from sklearn.metrics import precision_score
print(precision_score(y_test, y_pred))
0.42168674698795183

# F値を表示
from sklearn.metrics import f1_score
print(f1_score(y_test, y_pred))
0.35000000000000003

分類器クラスを作成する箇所以外は、ロジスティック回帰と同じ実装というのが分かると思います。また、分類器クラスのパラメータをチューニングすることで、精度の向上や過学習の抑止を図ることができます。

詳細は以下のリファレンスを参照してください。
参考：https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html

K近傍法（KNN）による学習と評価

続いて、K近傍法を検証してみます。

sample.ipynb

from sklearn.neighbors import KNeighborsClassifier

# 分類器を作成（K近傍法）
clf = KNeighborsClassifier(n_neighbors=9)

# 学習
clf.fit(X_train, y_train)

# 予測
y_pred = clf.predict(X_test)

# 正解率を表示
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_pred))
0.68

# 適合率を表示
from sklearn.metrics import precision_score
print(precision_score(y_test, y_pred))
0.31543624161073824

# F値を表示
from sklearn.metrics import f1_score
print(f1_score(y_test, y_pred))
0.3533834586466166

こちらも、分類器クラスを作成する箇所以外は、ロジスティック回帰と同じ実装です。また、分類器クラスのパラメータでは、n_neighbors（多数決をとるデータ数）の設定が肝と言えます。

詳細は以下のリファレンスを参照してください。
参考：https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html

ランダムフォレストによる学習と評価

最後に、ランダムフォレストを検証してみます。

sample.ipynb

from sklearn.ensemble import RandomForestClassifier

# 分類器を作成（ランダムフォレスト）
clf = RandomForestClassifier(
  random_state=100,
  n_estimators=50,
  min_samples_split=100
)

# 学習
clf.fit(X_train, y_train)

# 予測
y_pred = clf.predict(X_test)

# 正解率を表示
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_pred))
0.7851162790697674

# 適合率を表示
from sklearn.metrics import precision_score
print(precision_score(y_test, y_pred))
0.5121951219512195

# F値を表示
from sklearn.metrics import f1_score
print(f1_score(y_test, y_pred))
0.35294117647058826

こちらも、分類器クラスを作成する箇所以外は、ロジスティック回帰と同じ実装です。また、分類器クラスのパラメータは必ずチューニングして、最適化しましょう。

詳細は以下のリファレンスを参照してください。
参考：https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html

過学習かどうかの判別方法

過学習はオーバーフィッティングとも言いますが、その名の通り、学習させたデータにだけフィットしてしまうモデルを作ってしまうことです。

過学習している傾向があるかを簡単に確認するには、学習データと評価データを共に予測に使用して、その正解率の差異を確認してみればよいかと思います。

sample.ipynb

# 分類器を作成（ランダムフォレスト）※パラメータなしで実施してみる
clf = RandomForestClassifier()

# 学習
clf.fit(X_train, y_train)

# 評価データを予測に使用して正解率を表示（通常の評価フロー）
y_pred = clf.predict(X_test)
print(accuracy_score(y_test, y_pred))
0.7609302325581395

# 学習データを予測に使用して正解率を表示
y_pred_for_train = clf.predict(X_train)
print(accuracy_score(y_train, y_pred_for_train))
0.9992892679459844

ランダムフォレストをパラメータなしで実行した場合に顕著な結果になったので、再現してみました。過学習している場合は、上記のように学習データによる予測結果が評価データの時と比べて、過度に高くなる傾向があります。

過去の有馬記念のデータで検証

続いては、過去の有馬記念のデータを使用して、予測した結果の的中精度を見ていきたいと思います。ここまでの各アルゴリズムによる学習と評価のあとに以下の処理を実施します。

sample.ipynb

# 有馬記念のrace_indexリスト
target_race_indexes = [
  '2015122706050810',
  '2016122506050910',
  '2017122406050811',
  '2018122306050811',
  '2019122206050811'
]

for idx in target_race_indexes:
  # 有馬記念の説明変数(X_target)と目的変数(y_target)を取得
  X_target = dataX_std[dataX_std.index == idx] 
  y_target = dataY[idx]

  # 予測
  y_pred = clf.predict(X_target)

  # 結果表示
  print('y=', idx[0:4], 'pred=', y_pred, 'result=', y_target.values, 'precision_score=', precision_score(y_target, y_pred))

各アルゴリズムの出力結果は以下の通りです。

sample.ipynb

# ロジスティック回帰の場合
y= 2015 pred= [0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0] result= [0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0] precision_score= 0.0
y= 2016 pred= [0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0] result= [1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0] precision_score= 0.3333333333333333
y= 2017 pred= [0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0] result= [0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0] precision_score= 0.6666666666666666
y= 2018 pred= [0 0 0 0 1 0 0 0 0 0 0 1 0 1 1 0] result= [0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0] precision_score= 0.5
y= 2019 pred= [0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0] result= [0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0] precision_score= 0.3333333333333333

# サポートベクターマシン
y= 2015 pred= [0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0] result= [0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0] precision_score= 1.0
y= 2016 pred= [1 1 0 0 0 1 0 0 1 0 1 0 0 0 0 0] result= [1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0] precision_score= 0.6
y= 2017 pred= [0 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0] result= [0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0] precision_score= 0.6666666666666666
y= 2018 pred= [0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1] result= [0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0] precision_score= 0.5
y= 2019 pred= [0 0 0 0 0 1 1 0 0 1 0 0 0 1 0 0] result= [0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0] precision_score= 0.75

# K近傍法
y= 2015 pred= [0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1] result= [0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0] precision_score= 0.2
y= 2016 pred= [1 1 0 0 0 0 0 0 1 0 1 0 0 1 0 1] result= [1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0] precision_score= 0.5
y= 2017 pred= [0 1 1 0 1 1 1 0 0 1 1 1 0 0 0 0] result= [0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0] precision_score= 0.375
y= 2018 pred= [1 0 0 0 0 0 0 0 1 0 1 1 0 0 1 1] result= [0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0] precision_score= 0.3333333333333333
y= 2019 pred= [0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1] result= [0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0] precision_score= 0.25

# ランダムフォレストの場合
y= 2015 pred= [0 0 0 1 0 0 1 0 1 1 0 1 0 0 0 0] result= [0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0] precision_score= 0.4
y= 2016 pred= [1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0] result= [1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0] precision_score= 1.0
y= 2017 pred= [0 1 1 0 0 1 0 0 0 1 0 0 0 0 1 0] result= [0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0] precision_score= 0.6
y= 2018 pred= [1 0 1 0 1 0 0 0 0 0 0 1 0 1 1 0] result= [0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0] precision_score= 0.3333333333333333
y= 2019 pred= [0 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0] result= [0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0] precision_score= 0.3333333333333333

想像は付いてましたが、1レースにつき複数の馬を**1 (3着以内)**と予測しています。本来なら、各レース単位で出走馬の相対的な比較をして、購入対象の馬を絞り込みたいのですが、現状の実装では、データ全体の中から、当該馬が購入対象になりえるか？という予測になっています。これは今後の課題にしたいと思います。

アルゴリズムの選定

これまでの各アルゴリズムの的中精度を表にまとめてみました。

アルゴリズム	全体の適合率	全体のF値	有馬記念の適合率（5年分）
ロジスティック回帰	0.42	0.40	0.0, 0.33, 0.66, 0.5, 0.33
サポートベクターマシン	0.42	0.35	1.0, 0.6, 0.66, 0.5, 0.75
K近傍法	0.32	0.35	0.2, 0.5, 0.38, 0.33, 0.25
ランダムフォレスト	0.51	0.35	0.4, 1.0, 0.6, 0.33, 0.33

どのアルゴリズムが最適かについては、使用するデータセットの特性やサンプル数、それこそ実施するタイミングでも変わってきます。その前提で、上記の結果を参考にしてサポートベクターマシンかランダムフォレストのどちらかを採用することにします。（ただし、サポートベクターマシンは過学習気味かもしれません）

分類確率で出走馬を順位付け

複数の馬を**1 (3着以内)**と予測しているため、このままでは使いづらい状況です。3着以内に分類される確率で出走馬を順位付けして、購入対象を絞り込みたいと思います。

sample.ipynb

# 有馬記念のrace_indexリスト
target_race_indexes = [
  '2015122706050810',
  '2016122506050910',
  '2017122406050811',
  '2018122306050811',
  '2019122206050811'
]

for idx in target_race_indexes:
  # 有馬記念の説明変数(X_target)と目的変数(y_target)を取得
  X_target = dataX_std[dataX_std.index == idx] 
  y_target = dataY[idx]

  # 予測（0か1に分類される確率を予測）
  y_pred_proba = clf.predict_proba(X_target)

  # 辞書に変換(key:馬番, value:1になる確率)
  keys = list(range(1, y_pred_proba[:, 1].size + 1))
  values = y_pred_proba[:, 1]
  pred_dict = dict(zip(keys, values))

  # 辞書のvalueの降順に結果表示
  print('y=', idx[0:4])
  print(dict(sorted(pred_dict.items(), key=lambda x:x[1], reverse=True)))

冗長ですが、以下のように出力されます。辞書のkeyが馬番で、valueが3着以内に分類される確率を表しています。（辞書はvalueの降順でソート済み）

sample.ipynb

y= 2015
{7: 0.5696133455536686, 9: 0.4905907696112562, 11: 0.49035299894918755, 13: 0.35007505837022596, 12: 0.34220680265218334, 3: 0.31354320341453473, 4: 0.30980352572486725, 6: 0.30215860817620876, 10: 0.28490440087889995, 16: 0.27909507104899467, 1: 0.27533238657398446, 8: 0.24462710225495993, 2: 0.24459098148537395, 14: 0.24457566067758357, 5: 0.2445741121569982, 15: 0.23657499952423014}
y= 2016
{1: 0.6170252668074172, 2: 0.6051853981429345, 11: 0.5713617761448656, 9: 0.477082991798865, 6: 0.46056067001143736, 12: 0.30720442615574284, 3: 0.30215860817620876, 13: 0.30215860817620876, 8: 0.3007077278874594, 16: 0.2824267715516374, 7: 0.24464207649468928, 10: 0.24460750167495196, 4: 0.24459032539440356, 5: 0.2445880535923202, 14: 0.24458580009313594, 15: 0.24457449358955205}
y= 2017
{10: 0.6170803259427108, 2: 0.617026799448752, 5: 0.4606653690190285, 11: 0.3979634800224914, 14: 0.34913956740973595, 15: 0.3483806159861276, 12: 0.30215860817620876, 4: 0.3021535584865604, 13: 0.30024466402472444, 9: 0.2922074543922137, 1: 0.28743844415935654, 8: 0.2835192845558853, 6: 0.24461953217712495, 7: 0.2445971287209923, 16: 0.24458997746828753, 3: 0.2398748266004306}
y= 2018
{15: 0.5931962545935543, 12: 0.5631034477026525, 13: 0.46364861217784636, 16: 0.4423252760260589, 10: 0.3453931564376497, 3: 0.31157557743661457, 14: 0.30392079440550224, 8: 0.303732258765211, 6: 0.30219848678824074, 2: 0.3021586072259061, 7: 0.302143337075652, 1: 0.2981084912586054, 4: 0.27316635690234087, 5: 0.2445861267179151, 11: 0.2445764568939144, 9: 0.2445733900887549}
y= 2019
{6: 0.6170145067552477, 7: 0.5872900780905845, 10: 0.4904861419159532, 14: 0.43700495515775173, 12: 0.3512586575980933, 2: 0.3087214186649427, 9: 0.30553764130552913, 15: 0.3021220272592637, 16: 0.24776137832454997, 11: 0.2446323520236049, 5: 0.2446088059727512, 13: 0.24459614207316613, 8: 0.24459434296808064, 1: 0.24458784939997164, 4: 0.24457367329291685, 3: 0.24452744515587446}

ポイントはpredict_probaメソッドを使用することで、0か1の分類結果ではなく、0か1に分類される確率を取得することができます。今回は1に分類される確率を使用しています。

2020年の有馬記念予想

さて、本題の有馬記念の予想をしていきましょう。

sample.ipynb

# 有馬記念のrace_index
target_race_index = '2020122706050811'

# 有馬記念の説明変数(X_target)を取得
X_target = dataX_std[dataX_std.index == target_race_index] 

# 予測
y_pred_proba = clf.predict_proba(X_target)

# 辞書に変換(key:馬番, value:1になる確率)
keys = list(range(1, y_pred_proba[:, 1].size + 1))
values = y_pred_proba[:, 1]
pred_dict = dict(zip(keys, values))

# 辞書のvalueの降順に結果表示
print(dict(sorted(pred_dict.items(), key=lambda x:x[1], reverse=True)))

上記の実装で、サポートベクターマシンとランダムフォレストによる予測をそれぞれ3回実施しようと思います。そして、3着以内に来る確率の高い馬を3頭ずつ抽出します。

サポートベクターマシン（SVM）による予測

回次	馬番	馬名	確率
1回目	5	ワールドプレミア	0.58
1回目	13	フィエールマン	0.48
1回目	15	オセアグレイト	0.42

回次	馬番	馬名	確率
2回目	5	ワールドプレミア	0.58
2回目	13	フィエールマン	0.58
2回目	14	サラキア	0.41

回次	馬番	馬名	確率
3回目	13	フィエールマン	0.55
3回目	5	ワールドプレミア	0.53
3回目	10	カレンブーケドール	0.42

ランダムフォレストによる予測

回次	馬番	馬名	確率
1回目	13	フィエールマン	0.63
1回目	5	ワールドプレミア	0.52
1回目	4	ラヴズオンリーユー	0.49

回次	馬番	馬名	確率
2回目	13	フィエールマン	0.64
2回目	5	ワールドプレミア	0.55
2回目	9	クロノジェネシス	0.54

回次	馬番	馬名	確率
3回目	13	フィエールマン	0.60
3回目	4	ラヴズオンリーユー	0.57
3回目	5	ワールドプレミア	0.56

5番のワールドプレミアと13番のフィエールマンが抜けていて、3番手は拮抗しているという予測結果になりました。ただ、3番手が毎回違う馬になるのは結構な違和感で、データサンプル数がそれほど多くないにも関わらず、train_test_splitを使用して、簡易的に学習データと評価データを分割しているのが影響しているように思えます。

今回はこのままでいくとして、今後の課題にしたいと思います。

さいごに

今回は、作成した学習モデルを実際に使ってみるという実践形式を経験してみましたが、やはり練習と本番は違い、色々な気づきを得ることができました。次回は、先送りにした課題の解決と汎用モデルの構築を進めていければと思います。

実際に馬券を購入して、キャプチャ画像をアップして締めようと思ったのですが、まだ発売が始まっていなかったです...残念。実際に購入したら追記しようと思います。

**2020/12/26追記：**予測結果を参考に、ワイド5-13を一点で購入しました。