最近では機械学習を取り入れたサービス開発も増え始め、私自身もそのディレクションをすることがあります。
ただ、データサイエンティスト、MLエンジニアと呼ばれる人々が作る学習モデルを盲目的に利用するだけの簡単なお仕事です、というのは否めず、初心者(私)が、機械学習の知識レベルを上げるために、簡単な学習モデルを作れるようになるまでの過程をまとめてみました。
※ 続編『機械学習の初心者がpythonで有馬記念を予想してみた』も書いたので、併せてご覧ください。
今回のゴール
pythonによる環境構築からスタートして、一番手っ取り早いと思われるロジスティック回帰による分類モデルを構築してみるところまで実施してみます。題材は趣味と実益を兼ねて、競馬予測モデルに挑戦してみます。
※なお、競馬の専門用語を使用してますが、不明な点は調べて頂ければと思います。
環境構築
前提
実施した環境は以下の通りです。
- Python:3.7.7
- pip:20.2.2
pipenvインストール
pythonの実行環境をpipenvを使って構築していくことにします。
$ pip install pipenv
pythonを実行する仮想環境を構築します。
$ export PIPENV_VENV_IN_PROJECT=true
$ cd <project_dir>
$ pipenv --python 3.7
PIPENV_VENV_IN_PROJECTは仮想環境をプロジェクトのディレクトリ配下(./.venv/)に構築する設定です。
ライブラリインストール
ここでは、最低限必要なライブラリをインストールしていきます。
$ pipenv install pandas
$ pipenv install sklearn
$ pipenv install matplotlib
$ pipenv install jupyter
インストール後、カレントディレクトリのPipfileとPipfile.lockが更新されています。
これらの4ライブラリは必須アイテムと言えるので、有無を言わさずインストールしましょう。
| ライブラリ | 用途 |
|---|---|
| pandas | データの格納と前処理(クレンジング、統合、変換など) |
| sklearn | 様々な機械学習アルゴリズムを使用した学習と予測 |
| matplotlib | グラフ描画によるデータ可視化 |
| jupyter | ブラウザ上で対話形式のプログラミング |
jupyter notebookの起動方法
$ cd <project_dir>
$ pipenv run jupyter notebook
...
To access the notebook, open this file in a browser:
file:///Users/katayamk/Library/Jupyter/runtime/nbserver-4261-open.html
Or copy and paste one of these URLs:
http://localhost:8888/?token=f809cb2bcb716ba5726912d43738dd51992d3d7f20942d71
or http://127.0.0.1:8888/?token=f809cb2bcb716ba5726912d43738dd51992d3d7f20942d71
ターミナルに出力されたlocalhostのURLにアクセスすることで、ローカルサーバでjupyter notebookをブラウジングできるようになります。
以上で、環境構築は完了です。
モデル構築
機械学習と一言で言っても、教師あり学習、教師なし学習、強化学習、ディープラーニングと種類は様々ありますが、今回は冒頭でも記載したように、簡単な学習モデルを作れるようになるために、教師あり学習の分類モデルを構築します。
機会学習のワークフロー
AWSの記事が分かりやすかったので、こちらを参照するといいと思います。
機械学習のワークフローってどうなっているの ? AWS の機械学習サービスをグラレコで解説

簡単にまとめると上記の流れになるかと思いますので、この順番で、学習モデルを構築していきます。
1. データの取得
競馬予測モデルを構築するということで、まずは過去の競馬データが必要になります。
インターネット上には競馬情報サイトをスクレイピングする方法なども紹介されてますが、将来的な運用を見据えて、JRAの公式データを購入して取得することにします。
取得データ:JRA-VAN データラボ
自分でデータを取得するプログラムを作るのもいいですが、あらかじめ提供されている無料の競馬ソフトを使ってデータをファイル出力する方法も可能です。(本筋の話じゃないので詳細は省きます。)
今回は以下の2種類のデータファイルを取得しました。データの対象期間は2015年〜2019年の5年分です。
| ファイル名 | データ種別 | データ説明 |
|---|---|---|
| syutsuba_data.csv | 出馬表データ | 開催されるレースの出走馬などが記載された番組表データ |
| seiseki_data.csv | 成績データ | 開催されたレースの着順などが記載された成績データ |
2. データの前処理
データの前処理とは
機械学習において、一番重要とも言われるステップがこちらです。取得したデータに合わせて、以下の処理を実施します。
データクレンジング
ノイズとなるデータを取り除いたり、欠損値を違う値で埋める作業などを行います。
データ統合
学習に必要なデータが、最初から一つにまとまっていることは稀であり、分散したデータを統合することで一貫したデータを生成します。
データ変換
モデルの品質を向上させるため、データを指定のフォーマットに変換するプロセスです。例えば、数値データを-1から1の範囲に収まるデータに標準化したり、犬か猫のどちらかが選択されているようなカテゴリーデータをダミー変数化して数値に変換するなど、様々なデータの加工を実施します。
競馬データの前処理
ここから実際に競馬データの前処理を実装してきますが、起動したjupyter notebookを使用すると、対話形式でデータの状態を確認しながらのプログラミングが可能です。
まずは、取得した競馬データをpandasのDataFrameにロードしますが、データの前処理を実施した結果、最終的には以下の構造にデータを加工しようと思います。
| データ項目 | 用途 | データ説明 |
|---|---|---|
| race_index | index | 開催されるレースを特定した識別ID |
| 本賞金 | 説明変数 | 出走馬の獲得賞金の合計金額 |
| 騎手名 | 説明変数 | 騎手名をダミー変数化して使用 |
| 3着以内 | 目的変数 | 出走馬の着順を3着以内なら1、4着以下なら0に変換 |
| 今回は出走馬の実力を測る特徴量として、各馬がこれまでに獲得した賞金の合計金額を使用します。また、騎手の手腕による差も大きいと考え、騎手名も採用しました。この二つの説明変数だけで、どの程度の予測精度になるか試してみます。 |
import os
import pandas as pd
# 出馬表データ
syutsuba_path = './data/sample/syutsuba_data.csv'
df_syutsuba = pd.read_csv(syutsuba_path, encoding='shift-jis')
df_syutsuba = df_syutsuba[['レースID', '本賞金', '騎手名']]
# 成績データ
seiseki_path = './data/sample/seiseki_data.csv'
df_seiseki = pd.read_csv(seiseki_path, encoding='shift-jis')
df_seiseki = df_seiseki[['レースID', '確定着順']]
DataFrameでは、以下のようにデータが構成されています。
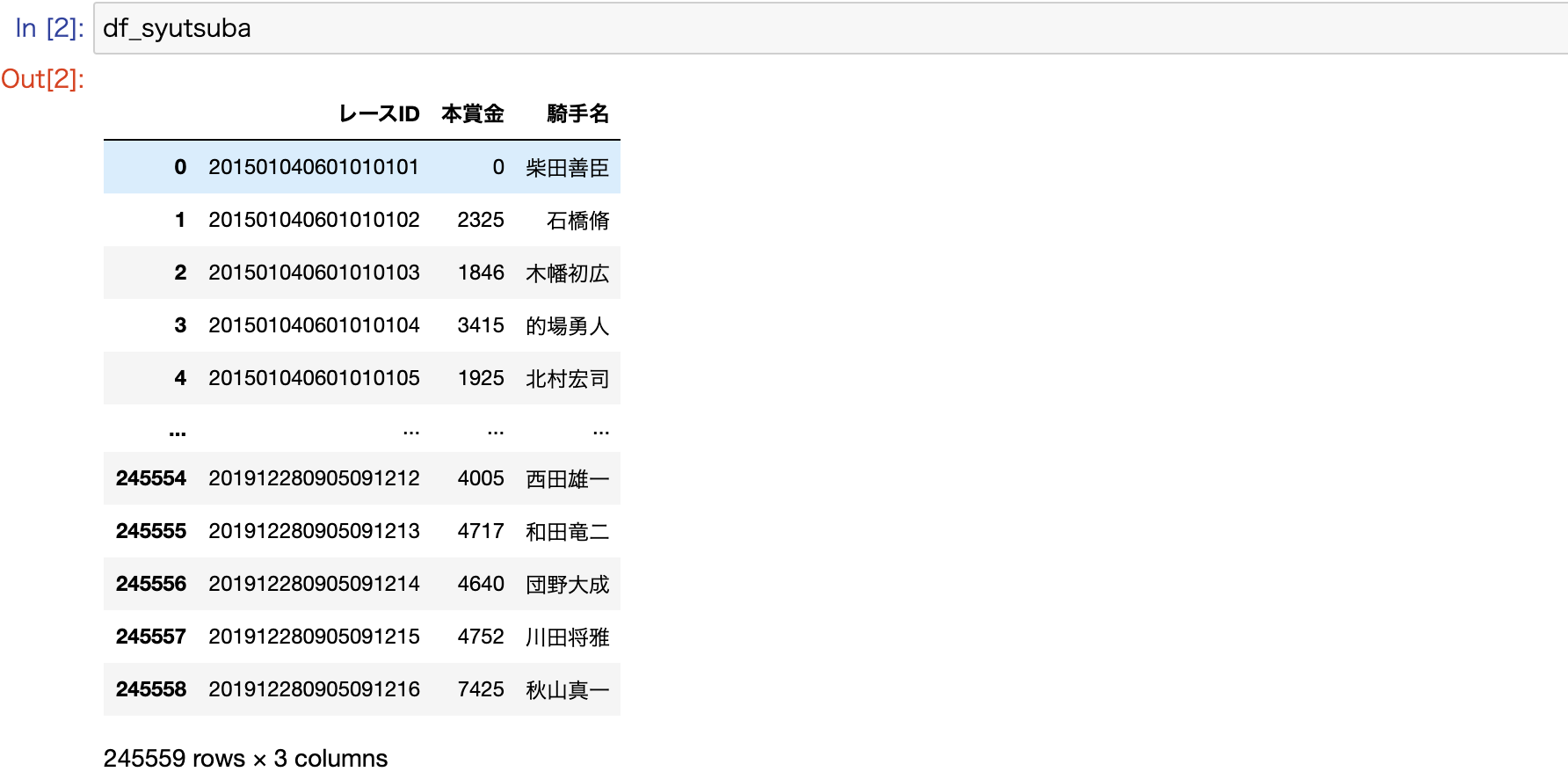
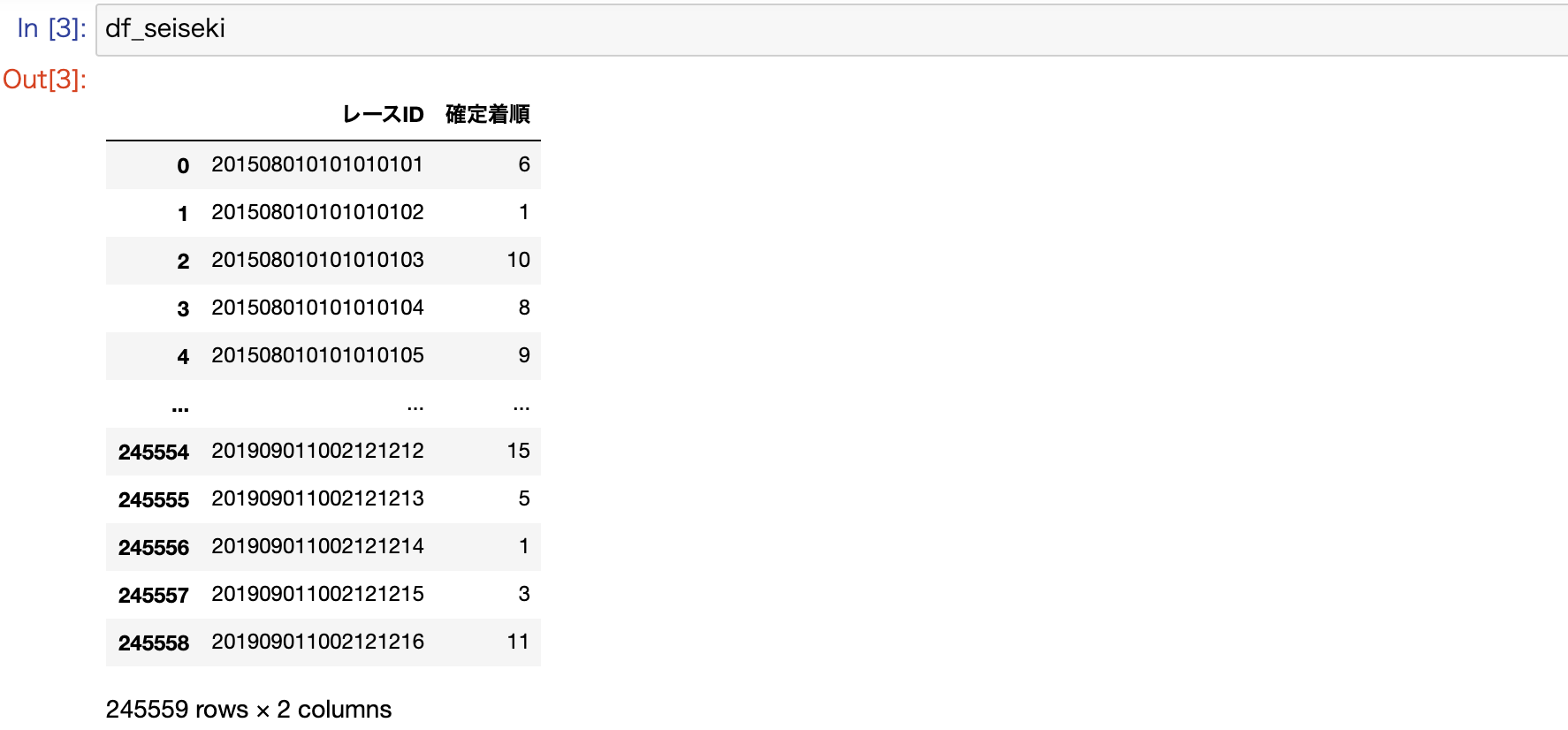
参考) レースIDのデータフォーマット
| 添字(レンジ) | データ長 | 項目説明 |
|---|---|---|
| 0〜3 | 4byte | 年 |
| 4〜5 | 2byte | 月 |
| 6〜7 | 2byte | 日 |
| 8〜9 | 2byte | 競馬場コード |
| 10〜11 | 2byte | 開催回次 |
| 12〜13 | 2byte | 開催日次 |
| 14〜15 | 2byte | レース番号 |
| 16〜17 | 2byte | 馬番 |
続いて、取得データを統合して、データのクレンジングや変換などを実施していきます。
# 出馬表データと成績データをマージ
df = pd.merge(df_syutsuba, df_seiseki, on = 'レースID')
# 欠損値があるレコードは除去
df.dropna(how='any', inplace=True)
# 着順が3着以内かどうかのカラムを追加する
f_ranking = lambda x: 1 if x in [1, 2, 3] else 0
df['3着以内'] = df['確定着順'].map(f_ranking)
# ダミー変数を生成
df = pd.get_dummies(df, columns=['騎手名'])
# インデックスを設定(レースだけを特定する場合は、16バイト目までを使用)
df['race_index'] = df['レースID'].astype(str).str[0:16]
df.set_index('race_index', inplace=True)
# 不要なカラムを削除
df.drop(['レースID', '確定着順'], axis=1, inplace=True)
DataFrameを確認すると、ダミー変数化したカラムは、そこに所属するカテゴリー数分の新たなカラムに置き換わって、0か1のフラグが設定されているのが分かります。
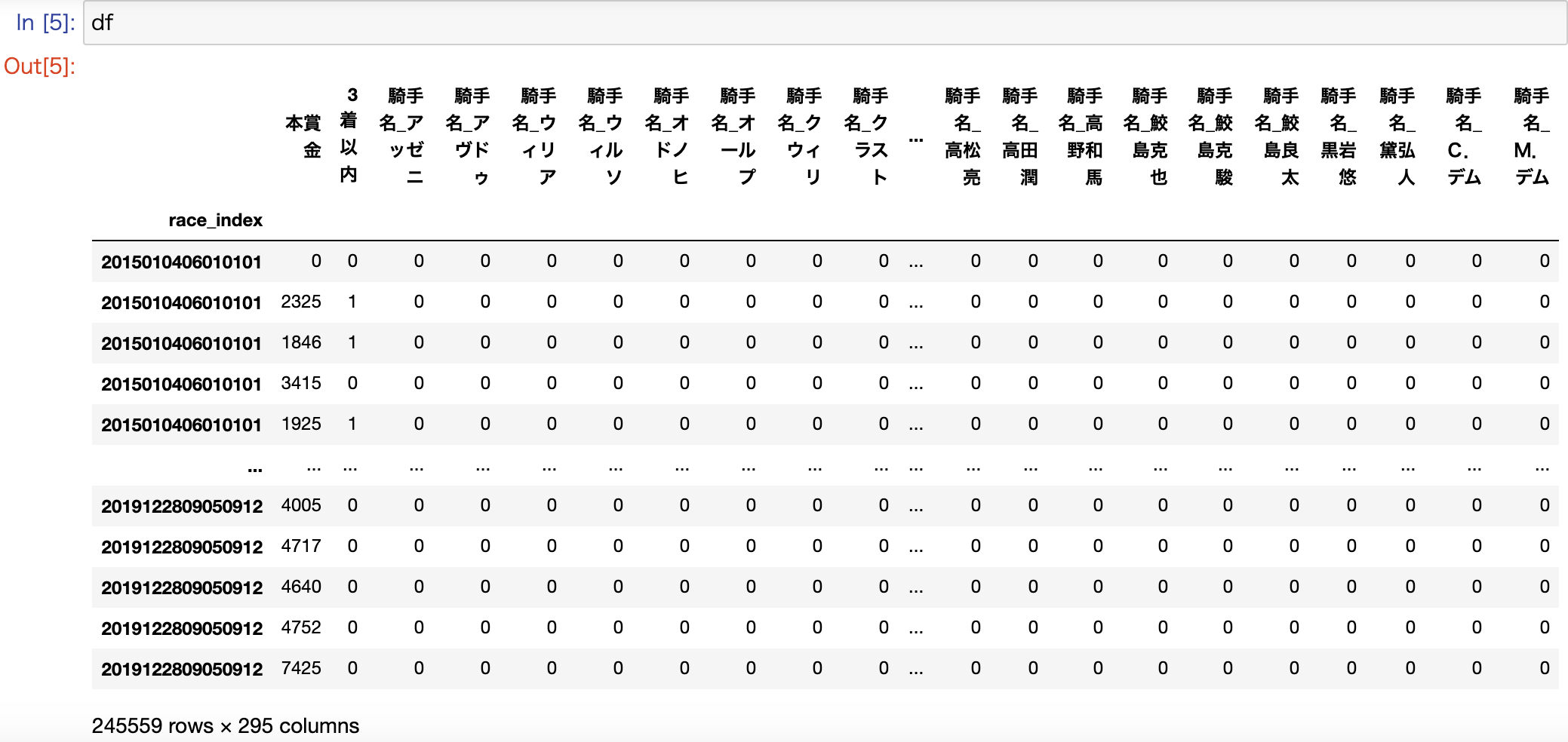
騎手名をダミー変数化したことで、カラム数が295まで増えてますが、カテゴリー数の多いカラムをダミー変数化すると過学習の原因にもなりますので、注意してください。
3. モデルの学習
続いてモデルの学習を行っていきましょう。
まず、データを説明変数と目的変数ごとに学習用データと評価用データに分割します。
from sklearn.model_selection import train_test_split
# 説明変数をdataXに格納
dataX = df.drop(['3着以内'], axis=1)
# 目的変数をdataYに格納
dataY = df['3着以内']
# データの分割を行う(学習用データ 0.8 評価用データ 0.2)
X_train, X_test, y_train, y_test = train_test_split(dataX, dataY, test_size=0.2, stratify=dataY)
要は以下の4種類のデータに分割しています。
| 変数名 | データ種別 | 用途 |
|---|---|---|
| X_train | 説明変数 | 学習データ |
| X_test | 説明変数 | 評価データ |
| y_train | 目的変数 | 学習データ |
| y_test | 目的変数 | 評価データ |
今回は、train_test_splitを使用して、簡易的に学習データと評価データを分割してますが、競馬のように、時系列の概念があるデータに関しては、**(過去)-> 学習データ -> 評価データ ->(現在)**という並びになるように、データを分割した方が、精度も上がると思われます。
続いて、用意したデータを学習させていきます。基本的なアルゴリズムならsklearnに内包されており、今回はロジスティック回帰を使用します。
from sklearn.linear_model import LogisticRegression
# 分類器を作成(ロジスティック回帰)
clf = LogisticRegression()
# 学習
clf.fit(X_train, y_train)
これだけで完了です。とても簡単ですね。
4. モデルの評価
まずは、評価データを予測して、その結果をもとに正解率を確認してみましょう。
# 予測
y_pred = clf.predict(X_test)
# 正解率を表示
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_pred))
0.7874043003746538
正解率は0.7874043003746538と78%も正しく予測できていることになります。
一見、「おーすげー!めっちゃ儲かるやん!」と喜んでしまいそうですが、このaccuracy_scoreには要注意です。続いて以下のコードを実行してみます。
# 混同行列を表示
from sklearn.metrics import confusion_matrix
print(confusion_matrix(y_test, y_pred, labels=[1, 0]))
[[ 339 10031]
[ 410 38332]]
この2次元配列は混同行列と言いますが、以下を表しています。
| 予測:3着以内 | 予測:4着以下 | |
|---|---|---|
| 実際:3着以内 | 339 | 10031 |
| 実際:4着以下 | 410 | 38332 |
このうち、正解率は予測:3着以内 × 実際:3着以内と予測:4着以下 × 実際:4着以下の合算値になります。
正解率:0.78 = (339 + 38332) / (339 + 38332 + 410 + 10031)
| 予測:3着以内 | 予測:4着以下 | |
|---|---|---|
| 実際:3着以内 | 339 | 10031 |
| 実際:4着以下 | 410 | 38332 |
| この結果から、3着以内と予測した件数がそもそも少なすぎて、大半を4着以下と予測していることで、正解率が押し上げられていることが分かります。 |
正解率には要注意というのが分かったところで、では何を基準にモデルの精度を評価すればいいかですが、この混同行列を活用した方法としては、F値を確認するという方法があります。
F値とは
以下の1と2を合わせたものになります。
1)3着以内と予測した出走馬のうち、正解した割合(適合率と言います)
2)実際に3着以内だった出走馬のうち、正解した割合(再現率と言います)
適合率:0.45 = 339 / (339 + 410)
再現率:0.03 = 339 / (339 + 10031)
| 予測:3着以内 | 予測:4着以下 | |
|---|---|---|
| 実際:3着以内 | 339 | 10031 |
| 実際:4着以下 | 410 | 38332 |
# F値を表示
from sklearn.metrics import f1_score
print(f1_score(y_test, y_pred))
0.06097670653835776
今回のF値を確認したところ、0.06097670653835776でした。F値ですが、ランダムに0と1に振り分けたケースの場合、0.5に収束する性質のものであるため、今回の0.06という値は極めて低い数値であるというのが分かります。
データ不均衡を修正
print(df['3着以内'].value_counts())
0 193711
1 51848
目的変数の3着以内と4着以下のデータ比率は1:4で、ややデータに偏りが見られますので、ここを少し是正してみます。
まず、追加で以下のライブラリをインストールします。
$ pipenv install imbalanced-learn
学習データの3着以内と4着以下のデータ比率を1:2にアンダーサンプリングします。アンダーサンプリングとは、少数データに合わせて多数データの件数をランダムに絞ることを意味します。
from imblearn.under_sampling import RandomUnderSampler
# 学習データをアンダーサンプリング
f_count = y_train.value_counts()[1] * 2
t_count = y_train.value_counts()[1]
rus = RandomUnderSampler(sampling_strategy={0:f_count, 1:t_count})
X_train_rus, y_train_rus = rus.fit_sample(X_train, y_train)
これで、データ不均衡を少し是正したので、再度モデルの学習と評価を実施します。
# 学習
clf.fit(X_train_rus, y_train_rus)
# 予測
y_pred = clf.predict(X_test)
# 正解率を表示
print(accuracy_score(y_test, y_pred))
0.7767958950969214
# 混同行列を表示
print(confusion_matrix(y_test, y_pred, labels=[1, 0]))
[[ 1111 9259]
[ 1703 37039]]
# F値を表示
print(f1_score(y_test, y_pred))
0.1685376213592233
F値が0.1685376213592233となり、かなり改善されましたね。
説明変数を標準化
説明変数が本賞金と騎手名の二つですが、騎手名はダミー変数化により0か1の値、一方で本賞金は以下のような特徴量の分布になっています。
import matplotlib.pyplot as plt
plt.xlabel('prize')
plt.ylabel('freq')
plt.hist(dataX['本賞金'], range=(0, 20000), bins=20)
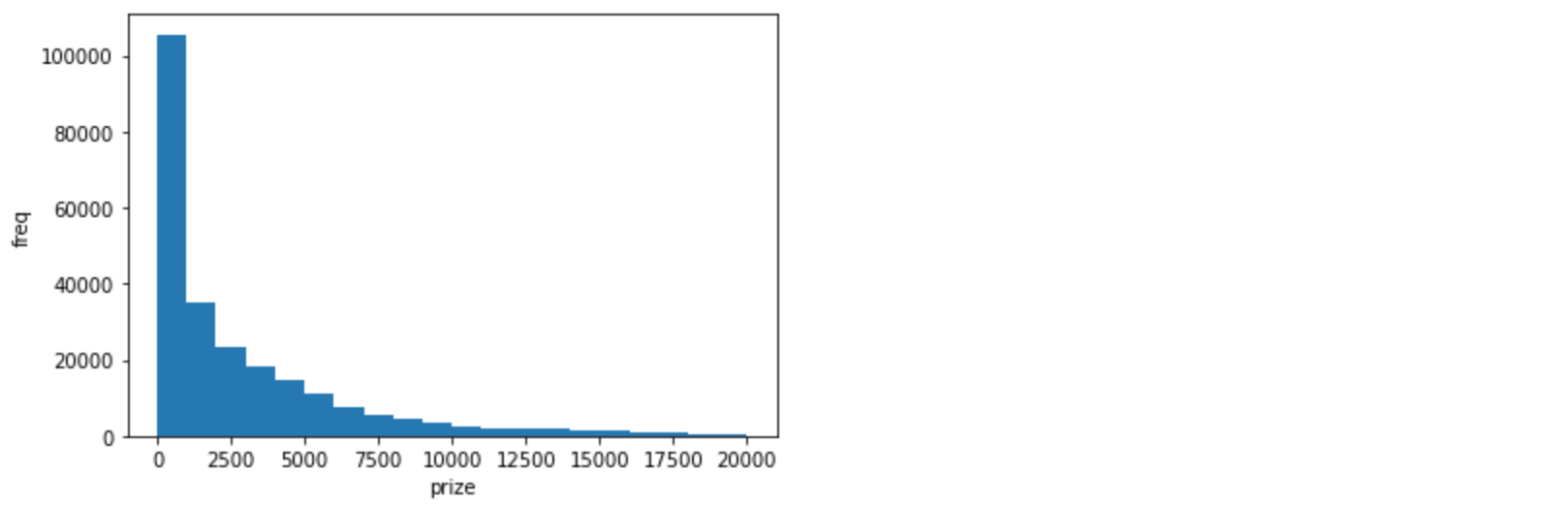
値の大きさが違いすぎるため、本賞金と騎手名を対等に比較できない可能性が高く、それぞれの特徴量を同じ範囲にスケールしてあげる必要があります。その手法の一つが標準化になります。
from sklearn.preprocessing import StandardScaler
# 説明変数を標準化
sc = StandardScaler()
X_train_rus_std = pd.DataFrame(sc.fit_transform(X_train_rus), columns=X_train_rus.columns)
X_test_std = pd.DataFrame(sc.transform(X_test), columns=X_test.columns)
標準化することで、全ての説明変数の値が一定の範囲内に収まるように変換されたので、再度モデルの学習と評価を実施します。
# 学習
clf.fit(X_train_rus_std, y_train_rus)
# 予測
y_pred = clf.predict(X_test_std)
# 正解率を表示
print(accuracy_score(y_test, y_pred))
0.7777732529727969
# 混同行列を表示
print(confusion_matrix(y_test, y_pred, labels=[1, 0]))
[[ 2510 7860]
[ 3054 35688]]
# F値を表示
print(f1_score(y_test, y_pred))
0.3150495795155014
F値が0.3150495795155014となり、前回からさらに精度向上し、30%台に乗りました。また、適合率が0.45、再現率が0.24で、競馬の予測結果としてはまずまずかと思います。
回帰係数の重みを確認
最後に説明変数のどの値が、競馬予測に強く影響しているかを回帰係数で確認します。
pd.options.display.max_rows = X_train_rus_std.columns.size
print(pd.Series(clf.coef_[0], index=X_train_rus_std.columns).sort_values())
騎手名_下原理 -0.092015
騎手名_左海誠二 -0.088886
騎手名_江田照男 -0.081689
騎手名_三津谷隼 -0.078886
騎手名_山本聡哉 -0.075083
騎手名_御神本訓 -0.073361
騎手名_伴啓太 -0.072113
騎手名_岩部純二 -0.070202
騎手名_武士沢友 -0.069766
騎手名_宮崎光行 -0.068009
...(省略)
騎手名_岩田康誠 0.065899
騎手名_田辺裕信 0.072882
騎手名_モレイラ 0.073010
騎手名_武豊 0.084130
騎手名_福永祐一 0.107660
騎手名_川田将雅 0.123749
騎手名_戸崎圭太 0.127755
騎手名_M.デム 0.129514
騎手名_ルメール 0.185976
本賞金 0.443854
本賞金が最も、3着以内に入ると予測するPositiveな影響を及ぼし、続いてはメジャーな騎手が影響度の上位を形成しているのが分かります。
5. モデルの運用
ここまでの作業で、モデルの構築を何とか実現することができました。次は実際の運用を考えてみましょう。競馬は毎週定期開催されていますが、毎レースの3着以内に入るであろう出走馬を予測して、あわよくばお金持ちになりたいと考えています。
では毎週、機械学習のワークフローを最初から順番に実施していきますか?1. データの取得は最新の出馬表データを取得するために毎回実施する必要がありますが、2. データの前処理と3. モデルの学習は毎回実施せずに、一度構築したモデルを再利用すればいいはずです(定期的なモデルのアップデートは必要ですが)。ということで、その運用を実施してみましょう。
import pickle
filename = 'model_sample.pickle'
pickle.dump(clf, open(filename, 'wb'))
このように、pickleというライブラリを使用することで、構築したモデルをシリアライズしてファイルに保存することができます。
そして、保存したモデルの復元方法がこちらです。
import pickle
filename = 'model_sample.pickle'
clf = pickle.load(open(filename, 'rb'))
# 予測
y_pred = clf.predict(予測対象レースの説明変数データ)
簡単にモデルを復元し、未来のレース予測に利用することができます。これでデータの前処理やモデルの学習を必要としない、効率的な運用が可能になります。
さいごに
以上で、環境構築からモデル構築まで、一連の作業を順を追って実施することができました。初心者による拙い説明にはなりますが、似たような境遇の方々の参考になれば幸いです。
次回は別のアルゴリズムを使って、今回作ったモデルとの比較検証や予測精度だけでなく、実際の収支はどうなのかという一歩踏み込んだ仕組み作りに挑戦したいと思います。