1.はじめに
Python 機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)の勉強会をしていて,読んでもRANSACが何かわからなかった(というかなんか色々勘違いした)ので調べました.
コードはsklearnにもすでにあるけど(sklearn.linear_model.RANSACRegressor),gifを作って一目でわかる(?)ようにしたのがこの記事です.
2.RANSACとは
2.1.目的
外れ値除いてモデルを学習させたい時に使う.
2.2.概要
以下の手順に従う.
- データをランダムにサンプリングする.(非復元抽出)
- モデルを学習する.
- 全てのデータに対して誤差を計算する.
- 3で求めた誤差から正常値と外れ値を決める
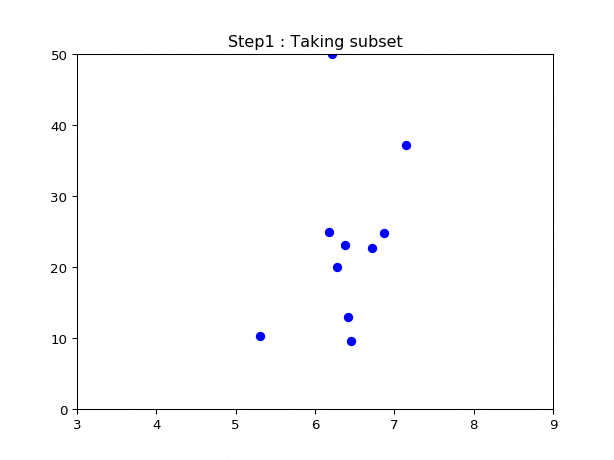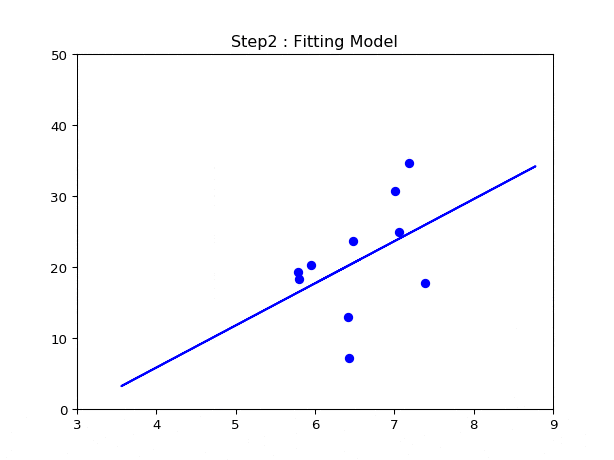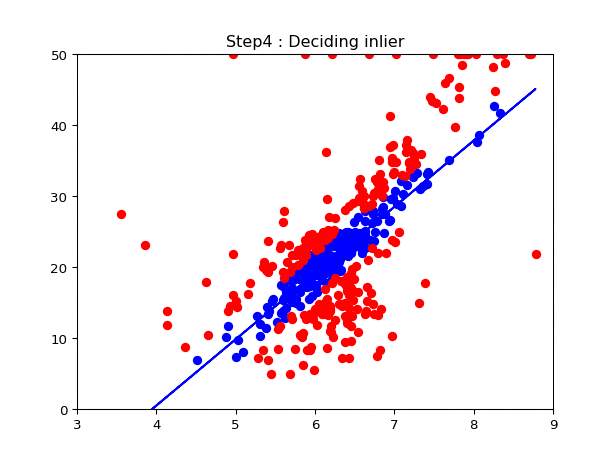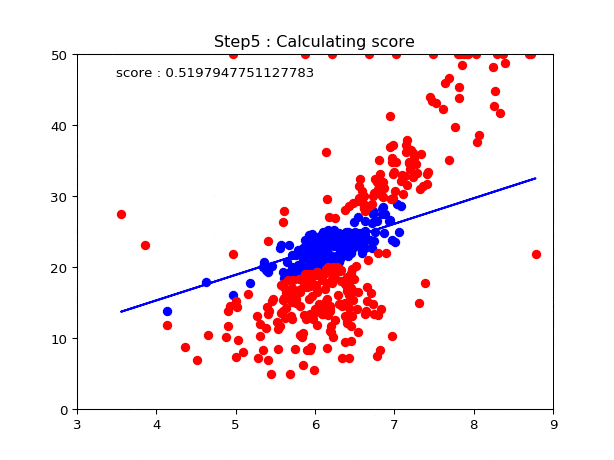
- 正常値のみでモデルの性能を評価する.
- 既定回数に達したら終了.そうでなければ1に戻る.
これを既定回数繰り返して,一番モデルの性能がよかったものを選ぶ.
ちなみにRandom sample consensusの略.
3.RANSACのgif
なにはともあれこんな感じです.
4.何回イテレーションすればいいか
この動画で何回イテレーションすればいいのかをお話していたので参考に紹介.
RANSAC: Random Sample Consensus I - Pose Estimation | Coursera
以下のように考えるようだ.
$N_{inlier}$は真のinlierの数,$N$は全sample数とする.
(ここで,真のinlierの数はresidualsから計算されたinlierか否かの予測値ではない.多分実用上は人がそれっぽく勝手に決めると思う.)
inlierを選ぶ確率は,
$$
w = N_{inlier} / N.
$$
$n$個サンプリングして,全部inlierからのサンプリングである確率は,$w^{n}$になる.
ということは,$n$個のサンプリングの中に,少なくとも1つ以上outlierが混じっている確率は,$1 - w^{n}$になる.
$k$回サンプリングを繰り返して,k回全てoutlierが混じっている確率は,$(1 - w^{n})^{k}$になる.
$k$回のサンプリングの中で,少なくとも一つoutlierが混じっていないサンプリングが存在する確率は,$1 - (1 - w^{n})^{k}$で,これを$p$とおくと,
$$
p = 1 - (1 - w^{n})^{k}
$$
$$
(1 - w^{n})^{k} = 1 - p,
$$
ここで,両辺の対数をとって$k$について解くと,
$$
k \log{(1 - w^{n})} = \log{(1 - p)}
$$
$$
k = \frac{\log{(1 - p)}}{\log{(1 - w^{n})}}.
$$
この$p$をこのくらいしっかりやりたいぞという値に決めて計算する.
5.code
参考にRANSACのコードは以下のようになる.
ちなみにこのコードはわかりやすさのために,sklearnのRANSACRegressorのコードを削っていってミニマムにしたやつ.
5.1.import
import copy
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
5.2.データのダウンロード
def load_data(return_df=False):
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/'
'housing/housing.data',
header=None,
sep='\s+')
df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS',
'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
X_cols = list(df.columns)
X_cols.remove("MEDV")
y_cols = ["MEDV"]
X = df.ix[:, X_cols].values
y = df.ix[:, y_cols].values
if return_df:
return df
else:
return X, y
def load_RM_MEDV():
df = load_data(return_df=True)
return df.RM.values, df.MEDV.values
5.3.ベースとなるモデル
class LinearRegression(object):
"""
Ex.
lr = LinearRegression()
lr = lr.fit(X, y)
y_hat = lr.predict(X)
print(lr.score(X, y))
"""
def __init__(self, add_const: bool=True):
self.add_const = add_const
self.weights = None
def predict(self, X: np.ndarray):
if self.weights is None:
raise ValueError("run .fit() before prediction")
if self.add_const:
X = self._add_const(X)
y_hat = X @ self.weights
return y_hat
def fit(self, X, y):
self.weights = self._least_squares(X, y)
return self
def _least_squares(self, X: np.ndarray, y: np.ndarray):
if self.add_const:
X = self._add_const(X)
beta_hat = np.linalg.inv(X.T @ X) @ X.T @ y
return beta_hat
def _add_const(self, X):
X_with_ones = np.c_[np.tile(1, len(X)), X]
return X_with_ones
def score(self, X, y) -> float:
y_hat = self.predict(X)
u = ((y - y_hat)**2).sum()
v = ((y - y.mean())**2).sum()
R_squared = 1 - u/v
return R_squared
def get_params(self):
return self.weights
def set_params(self, weights):
self.weights = weights
5.4.RANSAC
class RANSACRegressor(object):
"""
Ex.
X, y = load_RM_MEDV()
lr = LinearRegression()
ransac = RANSACRegressor(base_estimator=lr, min_samples=10, residual_threshold=3, max_trials=10)
ransac = ransac.fit(X, y)
ransac.best_model.predict(X)
"""
def __init__(self, base_estimator=None, min_samples=None,
residual_threshold=None, max_trials=100):
self.base_estimator = base_estimator
self.min_samples = min_samples
self.residual_threshold = residual_threshold # to decide inliners
self.max_trials = max_trials
def fit(self, X, y):
if self.base_estimator is None:
raise ValueError("set .base_estimator")
if self.min_samples is None:
# assume linear model by default
min_samples = X.shape[1] + 1
if self.residual_threshold is None:
raise ValueError("set .residual_threshold")
if self.max_trials is None:
raise ValueError("set .max_trials")
model_list = []
score_list = []
inlier_idxs_list = []
n_inliers_subset_list = []
subset_index_list = []
i_trial = 0
sample_idxs = np.arange(X.shape[0])
while i_trial < self.max_trials:
print(i_trial, "step")
estimator = copy.deepcopy(self.base_estimator)
# random sampling
subset_idxs = np.random.choice(len(X), self.min_samples, replace=False)
X_subset = X[subset_idxs]
y_subset = y[subset_idxs]
# fit model to subset data
estimator = estimator.fit(X_subset, y_subset)
# predict all data and calc resdiuals
y_hat = estimator.predict(X)
residuals = self._absolute_loss(y, y_hat)
# calc inlier
inlier_mask_subset = residuals < self.residual_threshold
inlier_mask_subset = inlier_mask_subset.flatten()
n_inliers_subset = np.sum(inlier_mask_subset)
inlier_idxs = sample_idxs[inlier_mask_subset]
X_inlier_subset = X[inlier_idxs]
y_inlier_subset = y[inlier_idxs]
# calc score of inlier data
score_subset = estimator.score(X_inlier_subset, y_inlier_subset)
# save models
model_list.append(estimator)
score_list.append(score_subset)
inlier_idxs_list.append(inlier_idxs)
n_inliers_subset_list.append(n_inliers_subset)
subset_index_list.append(subset_idxs)
i_trial += 1
# save best model
best_index = np.argmax(score_list)
self.best_index = best_index
self.best_model = model_list[best_index]
self.best_inlier_idxs = inlier_idxs_list[best_index]
# save log
self.model_list = model_list
self.score_list = score_list
self.inlier_idxs_list = inlier_idxs_list
self.n_inliers_subset_list = n_inliers_subset_list
self.subset_index_list = subset_index_list
return self
def _absolute_loss(self, y, y_hat):
loss = np.abs(y - y_hat)
return loss
5.5.実際に使う
X, y = load_RM_MEDV()
lr = LinearRegression()
ransac = RANSACRegressor(base_estimator=lr, min_samples=10, residual_threshold=3, max_trials=10)
ransac = ransac.fit(X, y)
6.備考
「Python 機械学習プログラミング」では,RANSACを
- ランダムな数のサンプルしてモデルを学習.
- 1で学習したモデルを用いて全てのデータに対して誤差を計算して,許容範囲となるデータ点を正常値とする.
- 2で正常値とみなしたデータに対して再びモデルを学習させる.
- 正常値に対するモデルの性能を評価する.
- モデルの性能がユーザーの閾値条件を満たすか,イテレーションが既定の回数に達したら終了.そうでなければ1に戻る.
と説明していた.
sklearnのコードを読むと,3の再びモデルを学習させるということはしていなかった.
確かに,モデルから近いところを集めてきているのでそれに対してまた学習しても大きな違いはないと思われる.
どちらが主流,もしくは良いのかは結局不明.
この記事ではsklearnのコードに準拠して3の正常値とみなしたデータに対して再学習はしていない.