三行で
- 自然界のデータにはたくさんノイズがある
- ノイズがあると、法則性をうまく見つけられないことがある
- そんなノイズをうまく無視するのがRANSAC
こんにちは。今日は大学院でやっているの情報学に関するネタをお送りします。
先日ふと、「そういえばちゃんと勉強したことがなかったなぁ」と思い立ったので、RANSACを勉強 & 実装してみました。
RANSACとは
大学院の研究で画像などの自然界のデータをとっていると、ノイズなどの原因で法則性から大きく外れて現れた「外れ値」がデータ中に含まれることがあります。外れ値は、データから法則性を見出す時に邪魔をします。そんな時に、外れ値をうまく無視して法則性(パラメータ)を推定をする手法がRANSACです。
...なんて概念の話では分かりにくいので、具体例を見てみましょう。以下、法則性を「モデル」と読み替えます。
直線のモデル推定
与えられた点群から、その点群がどんな直線に沿っているのかを推定する問題を考えます。
この直線に沿って点群が分布しているのですが、100サンプルに一つ上に大きく跳ねる外れ値が混ざっています。
グラフにすると、こんな感じです。

(pythonによる生成コード)
# true values
_a = 0.5
_b = 0.3
# samples
# samples
points = np.array([[x, _a * x + _b + .1 * np.random.randn() + (np.random.randint(100) == 0) * np.random.rand() * 1000] for x in np.arange(0, 10, 0.01)])
直線は y = ax + b で表されるので、この問題はaとbの値を求めることと同義です。
今回は、aの真の値を0.5, bの真の値を0.3としておきます。
この(a, b)を普通に求めようとすると、「外れ値」に引っ張られて推定する直線が大きく上に引っ張られてしまいます。例えば、最もオーソドックスな最小二乗法という手法だとこんな感じになってしまします。
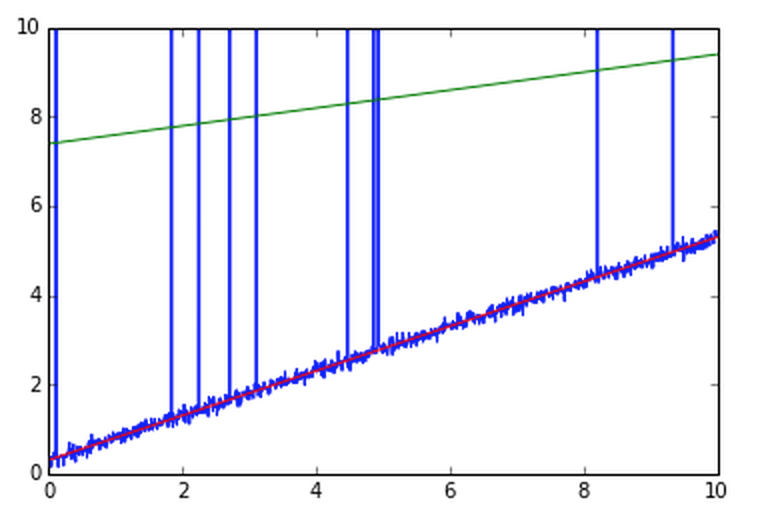
赤色が真の直線、緑色が推定された直線です。推定されたパラメータは(a, b) = (0.20, 7.4) となっています。このように、外れ値の影響で緑色の推定された直線が、真の赤い直線よりも大きく上に引っ張られてしまいます。
(pythonによる生成コード。焼きなまし的アプローチで)
def leastSquare(data):
# Simulated Annealing
tau = 100
bestfit = None
besterr = float('inf')
model = np.zeros(2)
while tau >= 0.0001:
for _ in range(10):
grad = errorGrad(model, data)
grad /= np.linalg.norm(grad)
grad *= -1
model += grad * tau
tau *= 0.1
return model
a, b = leastSquare(points)
RANSACで解決
このように普通に求めると「外れ値」が邪魔してどうにもうまくいかないので、外れ値をうまく無視します。RANSACでは以下のようなアルゴリズムを用います。
- データ集合から、モデルの決定に必要な数以上の「少数の」サンプルをランダムに選ぶ(今回は未知数が(a, b)なので2つ以上)
- 得られた「少数の」サンプルから最小二乗法などで臨時のモデルを導出する
- 臨時のモデルをデータに当てはめてみて、外れ値がそれほど多くなければ「正しいモデル候補」に加える
- 2-3を何回か繰り返す
- 得られた「正しいモデル候補」の中で、もっともデータによく合致するものを真のモデルとする
3.のステップで外れ値がたくさん出ている時は、2. のステップのサンプルで外れ値を捕まえてしまった場合なので無視します。このようにすることで外れ値の影響をうまい具合に除外して真の値を求めることができます。
言い換えると、データの点群の中で真のモデルをもっともうまく代表している点群を探し出し、その点群から直線を求めるという行為になります。
このRANSACでも求めた直線は以下のとおりです。

緑色が推定された直線です。データの分布にビッチリ寄り添っているのが確認できます。(a, b) = (0.496228..., 0.299107...)で、真の値にかなり近いことが確認できます。
pythonによるコードはこんな感じです。
def ransac(data,
# parameters for RANSAC
n = 2, # required sample num to decide parameter
k = 100, # max loop num
t = 2.0, # threshold error val for inlier
d = 800 # requrired inlier sample num to be correnct param
):
good_models = []
good_model_errors = []
iterations = 0
while iterations < k:
sample = data[np.random.choice(len(data), 2, False)]
param = getParamWithSamples(sample)
inliers = []
for p in data:
if (p == sample).all(1).any(): continue
if getError(param, p) > t:
continue
else:
inliers.append(p)
if len(inliers) > d:
current_error = getModelError(param, data)
good_models.append(param)
good_model_errors.append(current_error)
iterations += 1
best_index = np.argmin(good_model_errors)
return good_models[best_index]
a, b = ransac(data)
まとめ
今回はRANSACのアルゴリズムについて、2パラメータの直線モデルを例にとって取り上げてみました。いろんな論文にでてくるのでかなり重要なアルゴリズムです。
自分はもともとかなりのアルゴリズム好きだったのですが、大学院に入ってからの1年ちょっとは実装など実践重視でいろんなアルゴリズムをブラックボックスとして扱っていたので、これからは折に触れてそれぞれのアルゴリズムの中身も追いかけてみたいなぁと思っています。
ちなみに、今回のコードはipython notebookのフォーマットでこちらにまとめてあります。