機械学習を学ぶのに最も適した教材と言われる、Machine Learning | Coursera を受講しているので、復習も兼ね学んだ内容を簡潔にまとめてみようと思います。
第四弾は、とうとうニューラルネットワーク (Neural Network)です。
過去の記事
Coursera Machine Learning (1): 機械学習とは?単回帰分析、最急降下法、目的関数
Coursera Machine Learning (2): 重回帰分析、スケーリング、正規方程式
Coursera Machine Learning (3): ロジスティック回帰、正則化
神経細胞と脳 (Neuron and Brain)
ロジスティック回帰は、回帰分析 (Regression)の考え方を用いて分類 (Classification)課題を解くことができる優れた方法でした。
予測式である仮定関数$h_\theta(x)$は以下のようになります。
z = \theta_0 x_0 + \theta_1 x_1 + ... + \theta_n x_n = \theta^{\mathrm{T}} x
\\
h_\theta(x) = \frac{1}{1 + e^{-z}}
ロジスティック(シグモイド)関数を用いて、無理矢理$0 \le h_\theta(x) \le 1$にしています。
説明変数$x$の値をかけ合わせたりして新しい説明変数を増やせば、多項回帰といって非線形分類 (Non-linear classification)も可能になるのでしたね。
ただ、説明変数を増やしていくときりがありません。例えばコンピュータービジョン (Computer Vision)の分野でピクセル毎の色彩強度を見ていくとき、「新しい説明変数としてpixel 1とpixel 2を掛け合わせたものを・・・」なんてやっていくと説明変数がインフレし、ロジスティック回帰では計算が追いつきません。
そこで、人間や動物は日々様々なこと(食べ物か、ゴミか、などなど)を分類して生きていることに注目し、じゃあ、**脳を真似たアルゴリズムを作れば分類課題に強いはずだ!ということで生まれた分野がニューラルネットワーク (Neural Network)**です。最近熱いDeep Learning (TensorFlowなど)も、ニューラルネットワークの進化形ですね。
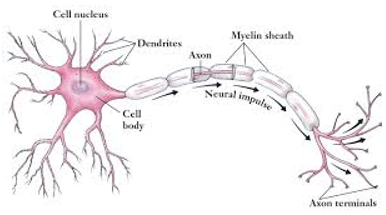
脳には様々な種類の細胞がいますが、そのうち情報処理を担当しているのが**神経細胞 (Neuron)**です。
(出典: http://keywordsuggest.org/gallery/332559.html)
人間の脳にはおおよそ10億もの神経細胞があり、互いに**シナプス (Synapse)と呼ばれる結合部位を介して繋がっています。シナプスは樹状突起 (Dendrite)上にあり、他の神経細胞から伸びてくる軸索 (axon)と繋がり、送られてくる情報を細胞体 (Cell body)**へ伝達します。細胞体は各樹状突起から送られてきた情報を統合、計算処理し、自分の軸索へ電気信号として出力します。
つまり、神経細胞という計算単位において、樹状突起というインプットを担当する部位と、軸索というアウトプットを担当する部位があり、他の神経細胞と繋がり情報の受け渡しをしている、ということです。
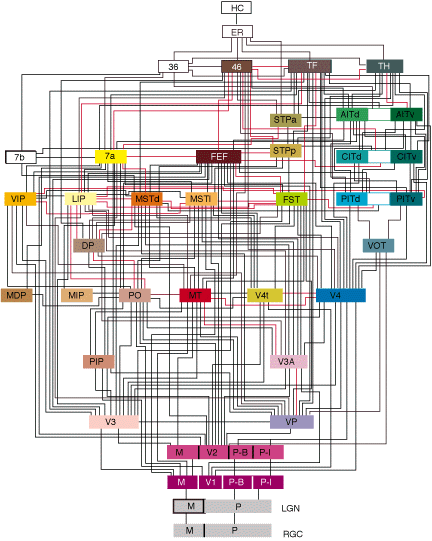
神経細胞同士のネットワークは、ただ闇雲に繋がっているわけではありません。おおざっぱに見ると**層構造 (Layer Structure)**になっていることがわかっています。
これは、脳の視覚野のネットワークを示したものです。目から情報が入り、低次から高次へレベルが上がって様々な脳のエリアへと情報が伝わり、処理されていることがわかります。
(出典: van Essen et al, Science, 1992)
これら、
- 神経細胞は、インプットとアウトプットの部位を持つ計算単位である
- 神経細胞同士のネットワークは、層構造を取る
という2つの特徴を使ったモデルが、ニューラルネットワークです。
#ニューラルネットワーク (Neural Network)#
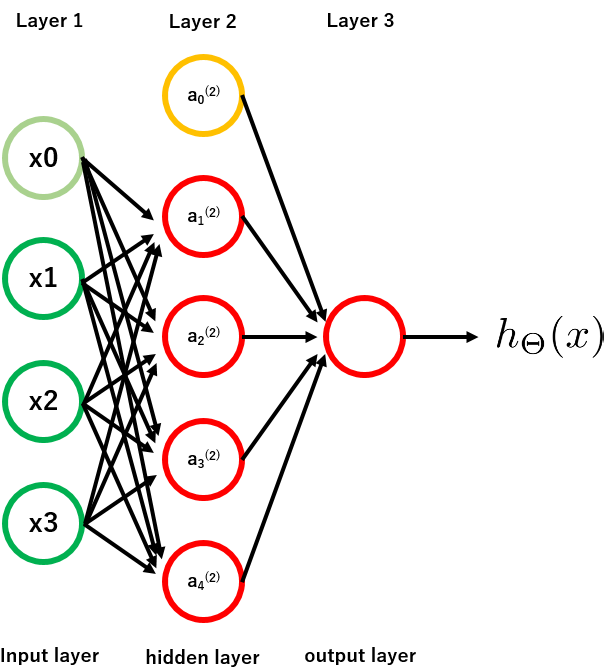
まずは簡単に、3層構造のニューラルネットワークを描画すると、以下のようになります。
インプット$X$からアウトプット$Y$を予測する際、その間にhidden layerが入ることで非線形の複雑な計算を可能にします。このhidden layerには、インプットでもアウトプットでもない**アクチベーションユニット (activation unit: $a_i ^{(j)}$)**というものが入っています。
**$a_i ^{(j)}$はレイヤー$j$のユニット$i$**という意味です。なので例えば、$a_2 ^{(3)}$はレイヤー$3$にあるユニット$2$ですね。
各アクチベーションユニットの値は、前のレイヤーからの入力によって決まります。具体的には、**ロジスティック回帰 (Logistic regression)**によって決まります。
レイヤー$j$からレイヤー$j + 1$への遷移を重み付けするパラメーターを$\Theta^{(j)}$とすると、レイヤー$j+1$にある$i$番目のアクチベーションユニット$a_i ^{(j+1)}$は、ロジスティック回帰により以下の式で表せます。
a_i ^{(j+1)} = g(\Theta_{i, 0} ^{(j)} a_0 ^{(j)} + \Theta_{i, 1} ^{(j)} a_1 ^{(j)} + ... + \Theta_{i, n} ^{(j)} a_n ^{(j)} )
パッと見、はぁ?となりますが、実際はただのロジスティック回帰です。$g$はロジスティック(シグモイド)関数ですね。
マッピングパラメーター$\Theta_{q, p} ^{(j)}$の意味が、**レイヤー$j$のユニット$p$ (つまり、$a_p ^{(j)}$)から、次のレイヤー$j+1$のユニット$q$ (つまり、$a_q ^{(j+1)}$)**への重み付けであることがわかれば、それほど難しくありません。
そのため、$\Theta ^{(j)}$の次元は、
(レイヤー$j+1$にあるユニット数)x(レイヤー$j$にあるユニット数 + 1)
になります。上図なら、例えば$\Theta ^{(2)}$の次元は4x(3+1)で4行4列です。なぜ前のレイヤーにあるユニット数に+1されているかというと、ロジスティック回帰における、いわゆる切片項$x_0$ (intercept)を含めるためです。上記の図でいうと、$x_0$や$a_1 ^{(2)}$がそうで、値は常に1です。
このように、各レイヤーのユニットの値を、前のレイヤーの全てのユニットを使ったロジスティック回帰で計算し、その値を使って更に次のレイヤーのユニットの値をロジスティック回帰で計算し・・・ということを、output layerにたどり着くまで繰り返すのが、ニューラルネットワークのアルゴリズムです。
というわけで、上記の3層構造の場合、仮定関数$h_\theta (x)$は以下のように表されます。
h_\Theta (x) = a_1 ^{(3)} = g(\Theta_{1,0} ^{(2)} a_0 ^{(2)} + \Theta_{1,1} ^{(2)} a_1 ^{(2)} + \Theta_{1,2} ^{(2)} a_2 ^{(2)} + \Theta_{1,3} ^{(2)} a_3 ^{(2)} + \Theta_{1,4} ^{(2)} a_4 ^{(2)} )
ニューラルネットワークによる非線形分類
単純な例として、インプットが$x_1, x_2$の2つしかなく、$0$か$1$のbinaryの場合を考えます。分類したアウトプット$y$の値も$0$か$1$です。
課題として、XORとXNORの論理演算を考えます。
XORは、2つの命題のいずれか一方が真のときに真になる論理演算、
XNORは、2つの命題が共に真、あるいは共に偽のときに真になる論理演算です。
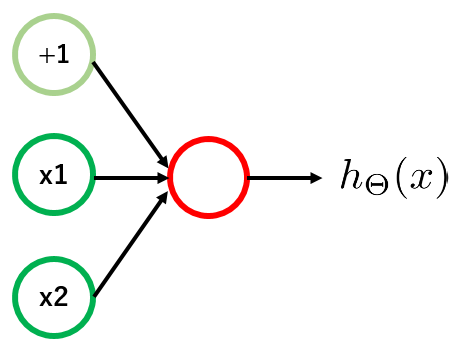
ニューラルネットワークも単純に、まずhidden layerなしの2層構造を考えます。
このとき、モデルのアウトプット$h_\theta (x)$は、以下のように表されます。
h_\Theta (x) = g(\Theta_{1,0} ^{(1)} + \Theta_{1,1} ^{(1)} x_1 + \Theta_{1,2} ^{(1)} x_2 )
このとき、例えば以下のように$\Theta$の値を決めると、上記の単純なネットワークは様々な論理演算をすることができます。
| $\Theta_{1,0}$ | $\Theta_{1,1}$ | $\Theta_{1,2}$ | 論理演算 |
|---|---|---|---|
| -30 | 20 | 20 | $x_1$ AND $x_2$ |
| -10 | 20 | 20 | $x_1$ OR $x_2$ |
| 10 | -20 | -20 | NOT($x_1$) AND NOT($x_2$) |
「この$\Theta$の値どっからきたの?」と思われるのは当然ですが、それは次回。
今回は、とりあえず$\Theta$をこのようにとると基本的な論理演算を単純なニューラルネットワークで実現できる、ということがわかればOKのようです。納得できない人は、$x = (0,0)(0,1)(1,0)(1,1)$のパターンを、それぞれの$\Theta$と一緒に$h_\theta (x)$の式に入れて計算してみてください。例えばANDの論理演算であれば、
| $x_1$ | $x_2$ | $h_\Theta (x)$ |
|---|---|---|
| 0 | 0 | $g(-30) \to 0$ |
| 0 | 1 | $g(-10) \to 0$ |
| 1 | 0 | $g(-10) \to 0$ |
| 1 | 1 | $g(10) \to 1$ |
と、$x = (1,1)$のときのみ$h_\Theta (x)$は真 (=1)になることがわかります。つまり論理演算ANDが実装されているわけですね。
XORは、XNORはそれより複雑な論理演算ですが、ニューラルネットワークを使うことでAND, OR, NOT AND NOTの組み合わせにより表現できます。
もともと2層だったニューラルネットワークにhidden layerを1層挿入し、$a_1 ^{(2)}$の値をAND、$a_2 ^{(2)}$の値をNOT AND NOTで計算します。そして、最終的なアウトプット$h_\Theta (x) = a_1 ^{(3)}$をORで計算します。すると、XNORが実現できます。
| $x_1$ | $x_2$ | $a_1 ^{(2)}$ | $a_2 ^{(2)}$ | $h_\Theta (x)$ | ||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | 0 | ||
| 1 | 1 | 1 | 0 | 1 |
XORの実現は、単純にXNORの$0$と$1$をひっくり返せばいいので、XNORを論理演算NOTを行うニューラルネットワーク$h_\Theta (x) = g(10 - 20x_1)$に通せば実現できます。
#まとめのまとめ#
- ニューラルネットワークは、神経細胞と脳のつくりを真似た分類アルゴリズムである。
- ニューラルネットワークは、ユニット同士が層状に結びついており、ユニットの値は前のレイヤーのユニットのロジスティック回帰により計算される。
- 遷移パラメーター$\Theta$の次元は、(遷移後のレイヤーのユニット数)x(遷移前のレイヤーのユニット数 + 1)
- 連続したロジスティック回帰の繰り返しにより、複雑な非線形の分類を行うことができる。
#終わりに#
今回はニューラルネットワークの入門編でした。個人的には、各ユニットの値が前のレイヤーのロジスティック回帰によって決まる、というのが面白かったです。それにより論理演算が実装できるというのは、実際に私たちの脳の中で起きていることかもしれません。専攻が脳科学の身としては、とても興味深い分野です。
次回は、どうやってニューラルネットワーク (Neural Network)に学習させるか、バックプロパゲーション (back propagation)のお話に入っていきます。