とりあえずこの映像を見てください。
昨日の勉強会の懇親会中に20分間のライブコーディングでシェーダーを作りました!
— かねた (@kanetaaaaa) 2019年6月19日
初めて人前でコーディングをしたんですが、めちゃくちゃ楽しかったです!!
(当日動かなかったpmod修正済です...)
差分
- q.x = abs(p.x ) - 10.;
+ q.x = abs(q.x ) - 10.;https://t.co/LH3TT4YzSU#klab_meetup pic.twitter.com/k61c3O2ZA1
20分間のライブコーディング映像フル
先日の #klab_meetup の懇親会で行った20分のライブコーディング映像を公開しました!
— かねた (@kanetaaaaa) 2019年6月21日
実況解説は@gam0022 さんと@songofsaya_さんです
突発ながら面白い実況で場を盛り上げてくださって非常に楽しかったです!
動画でもこの空間の楽しさが伝わると思うので是非ご覧ください!https://t.co/1CDeXMfJlT
この映像はGLSLという言語を利用して20分間のライブコーディングで無から作成されたものです。
20分という短い時間で無からこのような映像を作成する魔法の習得方法をこの記事ではお伝えします。
はじめに
6/19にKLab TechMeetup #4でシェーダーライブコーディングのすすめという題で登壇をしてきました。
この記事はその発表を記事向けにブラッシュアップしたものと、その日の懇親会で実際に行った20分ライブコーディングのテクニック解説記事になります。
当日利用した資料はこちらです
https://docs.google.com/presentation/d/1n_L8VJZs-Ig4FrlaUe5X2dhFB77ZPbiDBirjkoM4Afc/edit#slide=id.g1276827f2e_0_5
この記事を見てほしい人
この記事を見てほしい人は以下のような人たちです!
- シェーダー好きな人!
- シェーダーだけで絵を出すのは難しそう...と思っている人!
- ゲーム制作中にうっかりシェーダーばかり書いてしまって進捗が出ない人!
こんな人たちに向けて、シェーダーライブコーディングという一生遊べる遊びをご紹介します!
ちなみにこれは自己紹介なので、この記事は自分に刺さる記事となっております!!
本記事はある程度シェーダーを触ったことがあるという人向けです。
まだシェーダーを書いたことがない... でもシェーダーライブコーディングがしたい!!という方は
こちらの連載を一通り読んでから本記事を読み進めていただくと理解できるようになるはずです。
https://qiita.com/doxas/items/b8221e92a2bfdc6fc211
シェーダーライブコーディングとは?
短時間のシェーダーライブコーディングで映像を作るということをします。
VJのパフォーマンスや競技として行われており、いわゆるシェーダー芸です。
競技?
この記事でおすすめするシェーダーライブコーディングは競技として行われているものです。
シェーダーライブコーディングは国内外で大会が行われており、レギュレーションによって差異はありますが、トーナメント形式等によって観客を湧かせるシェーダーを競います。
競技の大きな特徴であり人を惹きつける部分は、制限時間があるという点と、必要な道具はすべて競技中に実装するという点だと僕は思っています。
できるだけ速く、できるだけ幅広い表現を突き詰めていくというのがシェーダーライブコーディングの醍醐味で、私たちはこれを目指して日々精進します。
そもそもシェーダー芸とは?
シェーダー(英: shader)とは、3次元コンピュータグラフィックスにおいて、シェーディング(陰影処理)を行うコンピュータプログラムのこと。「shade」とは「次第に変化させる」「陰影・グラデーションを付ける」という意味で、「shader」は頂点色やピクセル色などを次々に変化させるもの(より具体的に、狭義の意味で言えば関数)を意味する。(引用元:wikipedia
wikipediaからシェーダーの定義を引用するとこのようなものです。
本来シェーダーとはこのような処理を記述するのに利用されます。(一例です)
- 世界にオブジェクトを配置するための座標変換(頂点シェーダー)
- 形状に色を付けるためのシェーディング(フラグメントシェーダー)
- 描画結果に味付けするための画像処理(ポストエフェクト)
かなり省略していますが、通常は上記のようなシーンで使用されるものです。
この記事を見ている大半の方もこのような認識だと思いますが、シェーダー芸はこのような通常のシーン以外の使われ方をしているものを指します。
競技におけるシェーダー芸とは?
シェーダー芸にもいろいろタイプがありますが、競技のシェーダーライブコーディングで行われているのは、短時間のフラグメントシェーダーコーディングで映像を作るということです。
正直これだけ聞いてもさっぱりわからないと思いますが、詳しい内容については後程「入門レイマーチング」の項で実際にどういったことをやっているのか説明します。
シェーダーライブコーディング4つの面白ポイント
面白ポイントその1「シェーダーのみで完結する」
私のようにゲームを作るよりもシェーダーを優先してしまう人間にとって、シェーダーの実装のみに注力してルックを作成できる点が最高です。
もちろんコーディングのみということはマウスがなくても遊べるので、私のようなGUIアレルギーの方でも安心して遊ぶことができます!
面白ポイントその2「まるで魔法に見える!」
テクニックを覚えていくことでどんどん表現の幅が広がります。また覚えたスキルがすぐに見た目で反映されるので実際にRPGで魔法を覚えているように自分の成長を実感できます。
正直今でも、その場でどんどんルックが完成されていく様は魔法のように見えます。
面白ポイントその3「隙間時間に遊べる!」
レギュレーションによって異なりますが、競技時間は大体30分前後です。
私の場合だと60分を目安に遊んでいます。
移動時間などの隙間時間で暇を潰せてよい感じです!
面白ポイントその4「宴会芸に使えるかも!?」
エンジニアの飲み会で急な宴会芸の振りに使えるかもしれません。
私もイベント当日の懇親会で、酒の勢いに任せて実際に20分間のライブコーディングを行いました!!
入門レイマーチング
そんな楽しいライブコーディングですが、3D表現のためにレイマーチングという技術が現在主流となっています。
ここからは、皆さんにシェーダーライブコーディングを入門してもらうため、レイマーチングで使用されるスフィアトレーシングと距離関数について解説します。
そもそもフラグメントシェーダーのみで映像を作るとは?
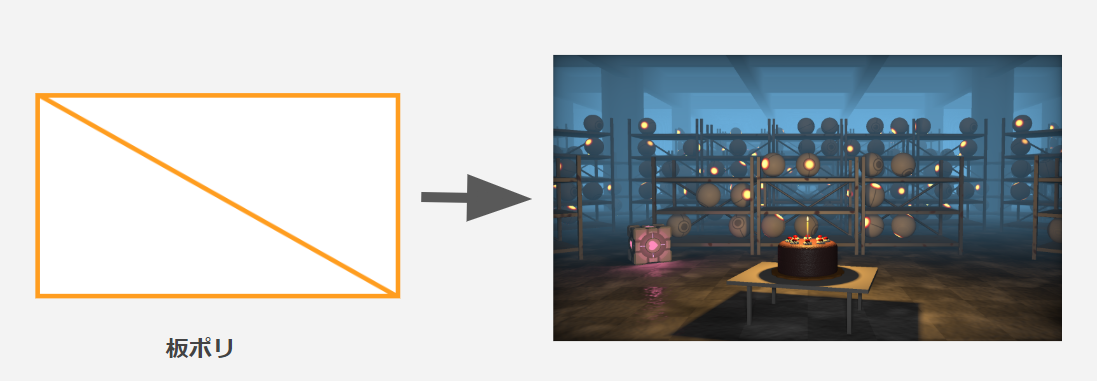
スクリーンを覆う板ポリに対してフラグメントシェーダーを適用してピクセル毎にシェーディング以外にもよしなな計算を行うということをします。
板ポリにシェーダーを適用するというと、大半の方はシェーダーの基本的な使い方の一つであるポストエフェクトを思い浮かべると思います。

実際ポストエフェクトとフラグメントシェーダー芸の処理の流れは似ています。

ポストエフェクトは事前に描画した結果をテクスチャから参照するのに対して、シェーダー芸ではその場で描画結果と同等のものを作成します。
そのためには形状の定義とトレースを行う必要があります。
形状をトレースする
形状を定義する前にこちらの方が理解しやすいため、まずはトレースする方法を解説します。
シェーダー内で定義したシーンをトレースするにはレイマーチングというテクニックを利用します。
単純なスクリーンスペースのエフェクトや、ParallaxOcculusionMappingを実装したことがある人は、オーソドックスな固定長のレイマーチングを思い浮かべるかもしれません。
シェーダー芸ではスフィアトレーシングという手法でレイを進めていきます。

スフィアトレーシングを実装する
では実際に実装しながら理解していきましょう。
この記事では実装の際にブラウザでGLSLが動作するGLSL Sandboxというサイトを利用します。
こちらのリンク先から新規シェーダーを作成してみてください。
http://glslsandbox.com/e
注意点
サイトを開くと初期コードはこのようなモノになっています。
# ifdef GL_ES
precision mediump float;
# endif
# extension GL_OES_standard_derivatives : enable
uniform float time;
uniform vec2 mouse;
uniform vec2 resolution;
void main( void ) {
vec2 position = ( gl_FragCoord.xy / resolution.xy ) + mouse / 4.0;
float color = 0.0;
color += sin( position.x * cos( time / 15.0 ) * 80.0 ) + cos( position.y * cos( time / 15.0 ) * 10.0 );
color += sin( position.y * sin( time / 10.0 ) * 40.0 ) + cos( position.x * sin( time / 25.0 ) * 40.0 );
color += sin( position.x * sin( time / 5.0 ) * 10.0 ) + sin( position.y * sin( time / 35.0 ) * 80.0 );
color *= sin( time / 10.0 ) * 0.5;
gl_FragColor = vec4( vec3( color, color * 0.5, sin( color + time / 3.0 ) * 0.75 ), 1.0 );
}
GLSL Sandboxでは以下の部分はエディタの実装上必要なおまじないコードです。
# ifdef GL_ES
precision mediump float;
# endif
# extension GL_OES_standard_derivatives : enable
uniform float time;
uniform vec2 mouse;
uniform vec2 resolution;
レイマーチングの仕組みを理解するうえでこれらは必要ないので、そのまま放置しておいてください。
ここからの解説ではmain関数にレイマーチングのアルゴリズムをゴリゴリ書いていくことになります。
まずはUVを表示する
gl_FragCoord(スクリーン座標)をresolution(画面解像度)で割って0 ~ 1のUV座標にします。
まずはこれをスクリーンにそのまま表示してみましょう。
シェーダーライブコーディングはこの状態から始まります。
void main( void ) {
vec2 uv = gl_FragCoord.xy / resolution.xy;
gl_FragColor = vec4(uv, 0.0, 1.0);
}
スクリーン空間を変更する
スフィアトレーシングでは画面に対してレイを飛ばしますが、このままではレイを定義するときに不便なので、-1 ~ 1の空間に変更します。
void main( void ) {
vec2 p = ( gl_FragCoord.xy * 2. - resolution.xy ) / min(resolution.x, resolution.y);
gl_FragColor = vec4(p, 0.0, 1.0);
}
カメラを定義
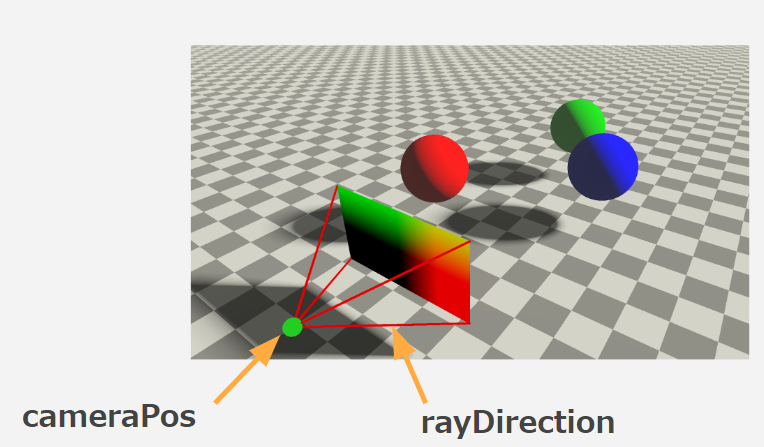
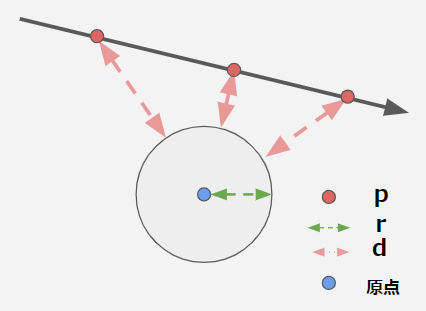
続いて、シーンを写すカメラの位置(cameraPos)を定義します。画像でいうところの緑の点です。
そして、先ほど作成した**-1~1のスクリーンを仮想的に空間に配置**して、カメラ位置から各ピクセルに向けたレイ(rayDirection)を定義します。画像でいうところの赤い線です。
これで描画に必要な視錐台を作ることができました。
void main( void ) {
vec2 p = ( gl_FragCoord.xy * 2. - resolution.xy ) / min(resolution.x, resolution.y);
vec3 cameraPos = vec3(0., 0., -5.);
float screenZ = 2.5;
vec3 rayDirection = normalize(vec3(p, screenZ));
gl_FragColor = vec4(p, 0.0, 1.0);
}
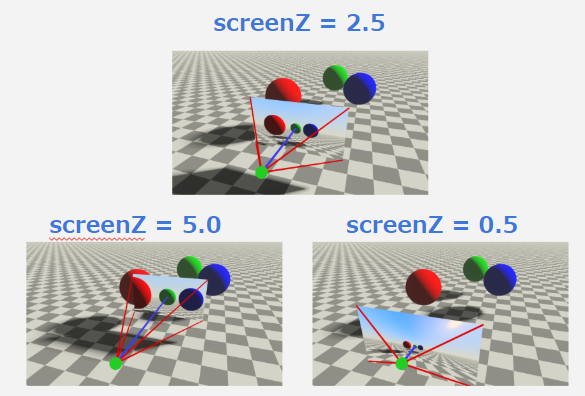
視野角について
レイの計算時にscreenZという変数がありましたが、これはスクリーン平面をどれだけカメラ位置から遠ざけるかの変数です。(スクリーンをレンズに見立てれば焦点距離(Focal Length)ということもできます。)
この値を大きくすると平面が離れて視野角が狭く、小さくすると近づいて視野角が広くなります。
レイ(光線)をマーチ(行進)する
視錐台を作れたら、肝であるスフィアトレーシングを実際に行っていきます。
カメラ位置(cameraPos)から空間に配置したスクリーンのピクセル方向(rayDirection)に形状に衝突するまでどんどんレイを進めていきます。
進める距離にはDistance Functionと呼ばれる、オブジェクト(今回は単純な球)への最短距離を出力とした関数を利用します。レイマーチングではこの関数を使って形状を定義します。
この最短距離を半径とした球の範囲内にはオブジェクトが存在しないことが保証されるので、その距離だけレイを安全に進めることができます。
このようにレイを行進する度に球がたくさん出てくるのでスフィアトレーシングと呼ばれています。
float distanceFunction(vec3 pos) {
float d = length(pos) - 0.5;
return d;
}
void main( void ) {
vec2 p = ( gl_FragCoord.xy * 2. - resolution.xy ) / min(resolution.x, resolution.y);
vec3 cameraPos = vec3(0., 0., -5.);
float screenZ = 2.5;
vec3 rayDirection = normalize(vec3(p, screenZ));
float depth = 0.0;
for (int i = 0; i < 99; i++) {
vec3 rayPos = cameraPos + rayDirection * depth;
float dist = distanceFunction(rayPos);
depth += dist;
}
gl_FragColor = vec4(p, 0.0, 1.0);
}
衝突したら色を決定する
距離関数で出力される距離が限りなく0に近づいたとき、レイがオブジェクトに衝突していると判定できるので、色を付けてマーチングループを早期終了します。
このタイミングでライティングなどのシェード処理を記述できますが、今回は単純に単色を設定します。
float distanceFunction(vec3 pos) {
float d = length(pos) - 0.5;
return d;
}
void main( void ) {
vec2 p = ( gl_FragCoord.xy * 2. - resolution.xy ) / min(resolution.x, resolution.y);
vec3 cameraPos = vec3(0., 0., -5.);
float screenZ = 2.5;
vec3 rayDirection = normalize(vec3(p, screenZ));
float depth = 0.0;
vec3 col = vec3(0.0);
for (int i = 0; i < 99; i++) {
vec3 rayPos = cameraPos + rayDirection * depth;
float dist = distanceFunction(rayPos);
if (dist < 0.0001) {
col = vec3(1.);
break;
}
depth += dist;
}
gl_FragColor = vec4(col, 1.0);
}
ここまでを全てのピクセルで実行する
今まで図では例のため、とあるピクセルに注目してスフィアトレーシングを行いましたが、これをすべてのピクセルに対して行います。
しかしこれについては深く考える必要はありません、既に画面を覆う板ポリのフラグメントシェーダーを使っているので自動的にこれが行われます。

スフィアトレーシングの仕組みはこれだけです、とても単純な仕組みであることが分かっていただけたと思います。
見た目は地味ですが、これはレイマーチングで描画されています!最初の一歩を踏み出せました!!

形状を定義する
続いて形状の解説です、先ほどのスフィアトレーシングの解説で**Distance Function(距離関数)**というものが出てきました。
スフィアトレーシングではシーンを構成するオブジェクトはこの関数を使って定義します。
たいそうな名前がついていますが、以下二つのシンプルな特性を満たしていればスフィアトレーシングで可視化することができます。
- 入力座標pからオブジェクトへの最短距離を出力する
- 外部なら正の距離、内部なら負の距離を出力する
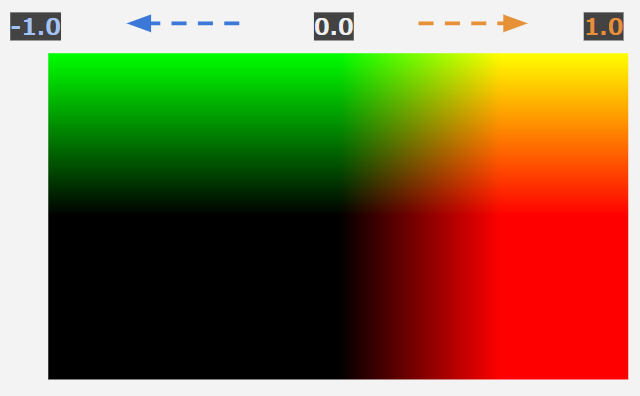
こちらの縞々模様の画像ですが、これは入力座標pをスクリーンのピクセル座標とした時の距離の等高線のようなものです。青が内部、オレンジが外部となっていて、本記事では距離関数の解説にはこの等高線を使います。

簡単な距離関数を紹介
球
float sdSphere(vec3 p, float r) {
float d = length(p) - r;
return d;
}
一つ目の球はとてもシンプルです。
原点からの**距離(length(p))から半径(r)**を引くだけで球までの最短距離となります。
平面
float sdPlane(vec3 p) {
float d = p.y;
return d;
}
続いて本記事で一押しする平面の距離関数です。
そして最もシンプルに定義できる距離関数でもあります。
三次元の入力座標の高さyをそのまま距離とすれば、xz平面の最短距離となります。
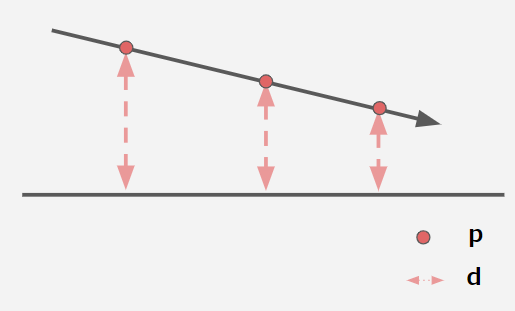
ライブコーディングをしばらく練習していると、平面の汎用性の高さにきっと気づくと思います。
少なくとも歴一か月の私はライブコーディング中にこの平面をめちゃくちゃ使います。どういうことかは次の話で分かると思います。
箱の距離関数を作ってみよう!
雑に二つ紹介しましたが、ライブコーディングでは自分で距離関数を構築するという場面が結構出てきます。
また初心者にとってレイマーチングでは距離関数のハードルがとても高いのではないかと思っています。実際に私も距離関数難しそう..となっていました。
その助けとなるために、ここからは私がライブコーディングでよく使う箱の距離関数を一緒に作ってみます。
実は距離関数は最短距離じゃなくてもいい!?
最短距離というと難しい距離関数ですが、Distance Estimator(距離推定器)とも呼ばれていて、実は必ずしも最短距離である必要はありません。
これと先ほど紹介した平面の距離関数を頭に入れておけば簡単に箱を作ることができます。では実際にやってみます。
ベースとなる平面を用意
例によって原点がスクリーンの中心にある-1~1の空間で話を進めます。
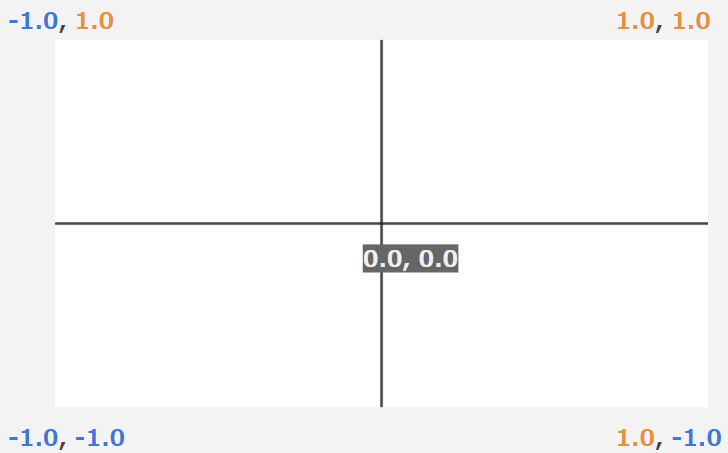
まず箱のベースとなる平面を二つ用意します。
一つ目はy座標を利用した平面。
float sdBox(vec3 p, float s) {
return p.y;
}
二つ目はx座標を利用した平面です。
float sdBox(vec3 p, float s) {
return p.x;
}
max関数による論理積演算
距離関数は、min, max関数を利用して簡単にブーリアン演算を行うことができます。
今回はmaxを利用して先ほどの二つの平面の積集合を取ります。もっと簡単に言うと二つの平面を比較して両方とも平面の内部である場所を残すという操作です。
(この例では、実際は3次元の箱の距離関数を構築するため、3つ目の軸であるp.zの平面も含まれています)
float sdBox(vec3 p, float s) {
return max(max(p.x, p.y), p.z);
}
距離関数のブーリアン演算については @gam0022 さんの 資料 が詳しいのでこちらをご参照ください。

正の領域を複製するというアイデア
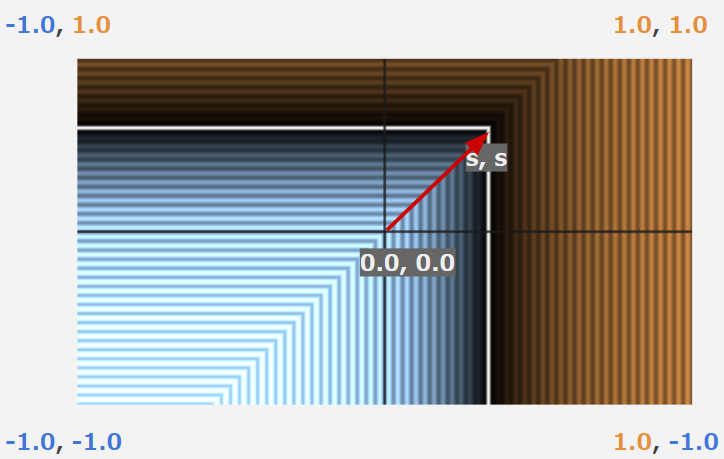
今のままでは崖のような形状でとても箱とは言えないので、おもむろに座標が正の方向にsだけ平行移動してみます。
float sdBox(vec3 p, float s) {
p = p - s;
return max(max(p.x, p.y), p.z);
}
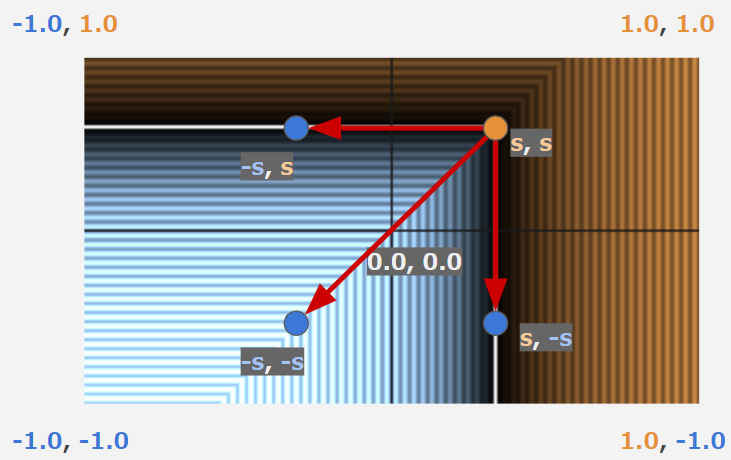
すると、この右上の領域を、その他の領域に鏡のように対称に配置すれば箱になるのではないかというのが見えてきます。
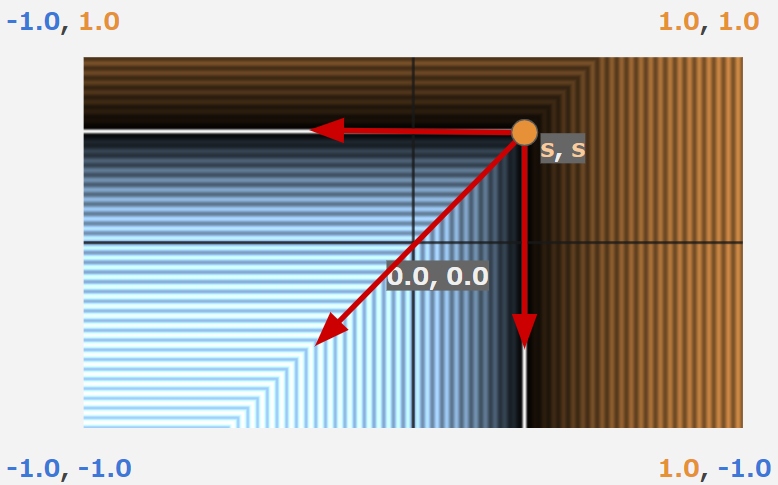
これは**Fold(フォールド)**というテクニックで実現できます。
座標のFold(折り畳み)による鏡像
Foldをするにはabsという絶対値を返す関数を座標に対して使っていきます。
理解しやすいように、今回はx座標のみをFoldしてみます。
vec2 foldX(vec3 p) {
p.x = abs(p.x);
return p;
}
こちらの例では中央の0.0より左側のマイナスの領域には何も表示されていません。
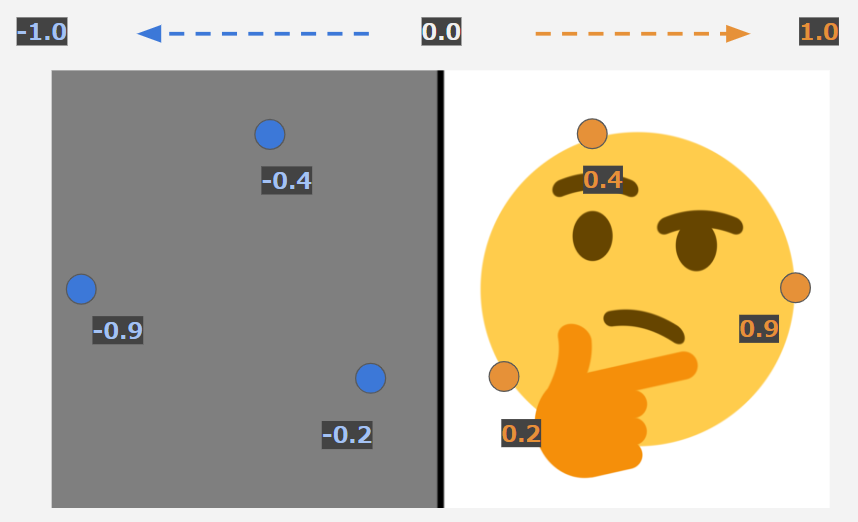
absによるFoldを行うことで、以下のように0.0を中心に座標の関係が対象になり鏡像が現れます。
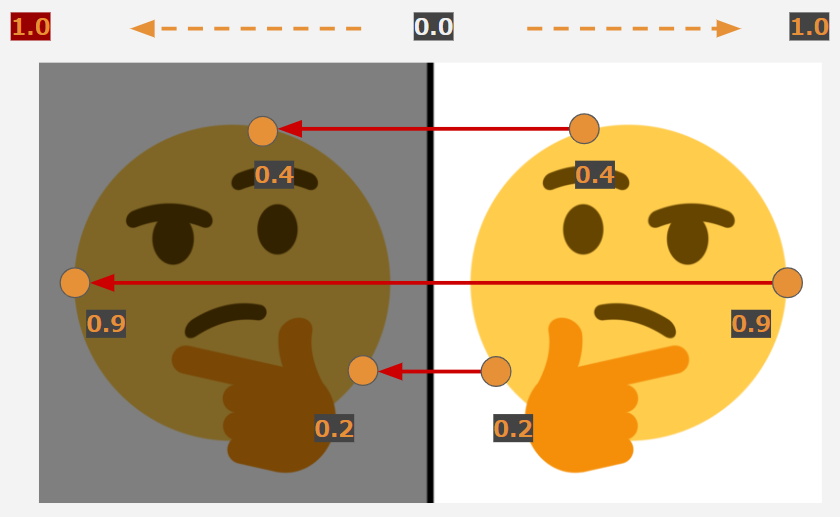
これは入力点に対して形状の内外判定を評価するという距離関数の特性だからこそできるテクニックです!
既存のいくつかの距離関数は、このテクニックを利用して処理コストを削減しています。
距離関数にFoldを適用して箱が完成!
今紹介したテクニックを先ほどの作りかけの距離関数に適用して見ます
absを利用したフォールドを行うことでマイナスだった領域に右上の部分が折りたたまれて鏡像が現れました。
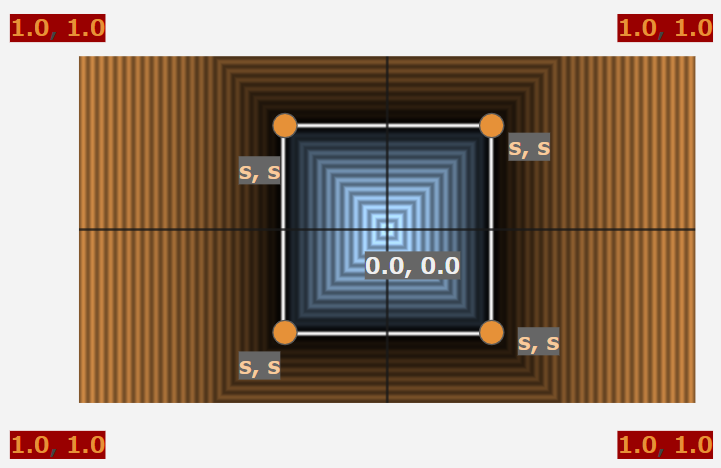
これだけで箱の距離関数が完成してしまいます!
float sdBox(vec3 p, float s) {
p = abs(p) - s;
return max(max(p.x, p.y), p.z);
}
absによって全ての座標が軸に対して対象になり、鏡像が表れているのが図を見たら分かるはずです。
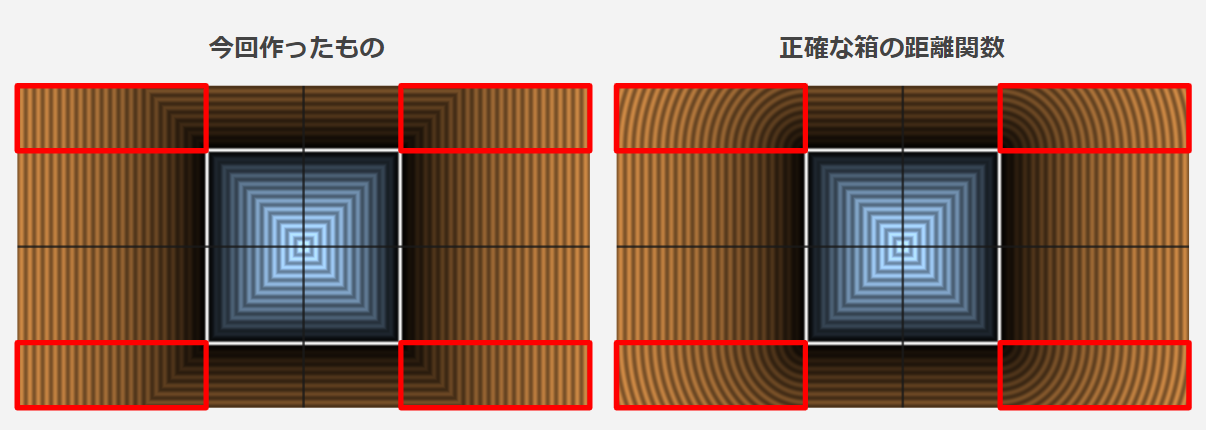
正確な距離関数と比較
今回作った距離関数は赤く囲ったあたりが正確ではありませんが、このように必ずしも最短距離でない関数でもスフィアトレーシングでは可視化することができます。
私の場合ライブコーディング中はできるだけ頭を使いたくないというのと、正確なものに比べてタイプ数が少なくなることが多いので、今回のような単純な平面の組み合わせで距離関数を構築するということをよくやります。
このように平面を覚えておくだけで結構いろんなパターンの形状を構築できます。
次は?
ここまでの内容で皆さんは画像のようなシーンを距離関数で定義して、スフィアトレーシングで可視化できるようになりました。
しかしシェーダーライブコーディングは事前準備やコピペができません、ここまでの内容をググらずコピペせずに書けるようになりましょう!
そしてスピードが命です、何も見ずに書けるようになったら3分で書けるようになってください!!!
そこまでできれば皆さんはシェーダーライブコーディングのほぼプロです。あとは細かいテクニックを覚えていくだけでできることがどんどん増えていきます。
好みの題材を見つけて今できる範囲で実際にコーディングしてみてもよいですし、次のテクニックが知りたいとなったら、シェーダーウィザードの方々の力を借りましょう。大体この辺りにいます。
また以前書いたこちらのリンク集も、シェーダーライブコーディングで使えるテクニックが多数あります。
是非こちらも参考にしてみてください
ここまでのまとめ
ここまででシェーダーライブコーディングの楽しさと遊び方をお伝えしました。
一人にでも多く「意外といけそう!とかこれは一生遊べるのでは?」と思っていただけたならうれしいです。
何度も言いますが、平面を覚えるだけで距離関数攻略だけでなくレイマーチングでの表現も広がってくるというのを覚えて頂けるとこれから入門するにあたって助けになると思います。
というわけで魔法使いになりたい人は、今すぐにシェーダーライブコーディングを始めてみてください!
当日行ったライブコーディングの解説

ここからは、イベント当日の懇親会で実際に私が20分でライブコーディングを行って完成したシェーダーの解説をしてみます。
今回作ったものは、この記事内で説明したスフィアトレーシングと距離関数をそっくりそのまま使って、プラスアルファでいくつかのテクニックを利用して作りました。
この記事の内容だけでもこんなものが作れるんだという目安にして頂きたいです。
map関数について
私はレイマーチングでシーンを定義するとき、全体のオブジェクトをmapという関数にまとめて記述します。
今回のmap関数を理解するにあたって距離関数にまつわる3つのテクニックを理解しておく必要があります。
Modによる複製
このテクニックは p.z = mod(p.z, 10.0) のように余剰を利用して距離関数のオブジェクトを複製するテクニックです。
これはとても有名なテクニックで日本でもたくさん情報があるので説明をそちらにお任せしようと思います。
こちらのページがとても詳しく解説してくださっています。
https://wgld.org/d/glsl/g012.html
Polar Modによる複製
当日は不慮の事故でお見せすることができなかったんですが、極座標で空間を分割してオブジェクトを複製するというテクニックです。
Shadertoyでは至る所でこのテクニックが使われていますが、日本の解説を見たことがなかったので頑張って解説してみます。
関連するコードはこちらです。
mat2 rot(float a) {
float c = cos(a), s = sin(a);
return mat2(c,s,-s,c);
}
const float pi = acos(-1.0);
const float pi2 = pi*2.;
vec2 pmod(vec2 p, float r) {
float a = atan(p.x, p.y) + pi/r;
float n = pi2 / r;
a = floor(a/n)*n;
return p*rot(-a);
}
rotというのは二次元の回転行列を作る関数です、piは円周率を覚えていないのでacos(-1.0)で横着しています。
本体はpmodという関数で、第一引数に座標、第二引数に空間を分割する数を取ります。
まず一行目を見てみましょう
float a = atan(p.x, p.y) + pi/r;
ここでは極座標系で分割するために、atan関数を用いて入力座標の角度を計算しています。
この時利便性のために分割角度の半分であるpi/rというオフセットを加えます。
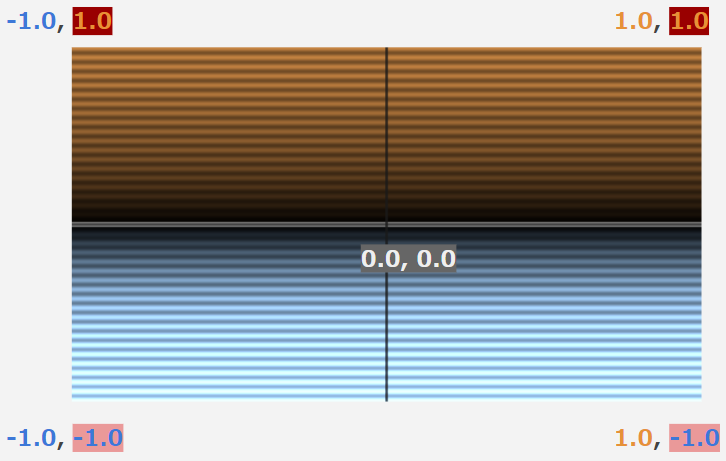
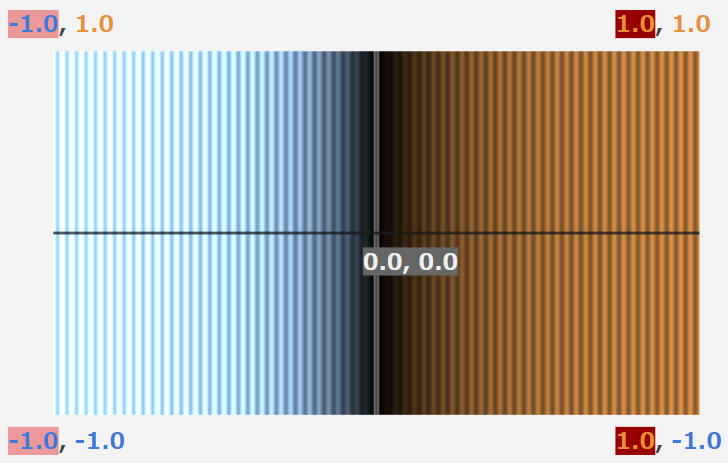
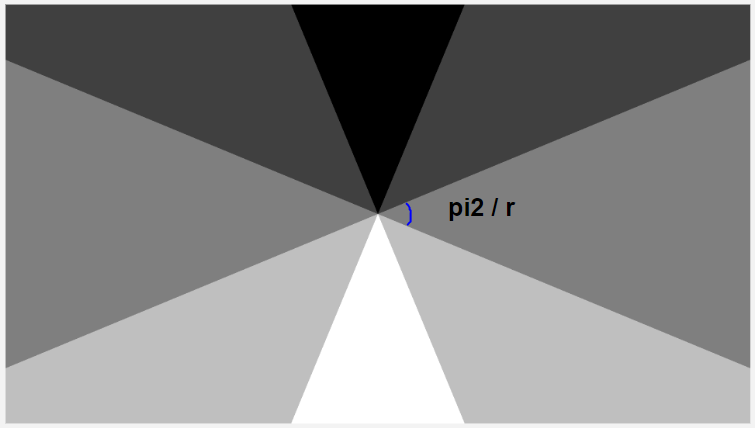
どういうことか説明するために、加えなかった時と加えた時の分割後の状態を比較してみます。

上の図の真っ黒なところが複製の基準となる、空間IDが0の領域です。この領域に存在するオブジェクトがその他の領域にも現れます。
見比べてもらうと一目瞭然だと思いますが、オフセットを加えていない場合、空間の切れ目が画面中央に存在していますよね?
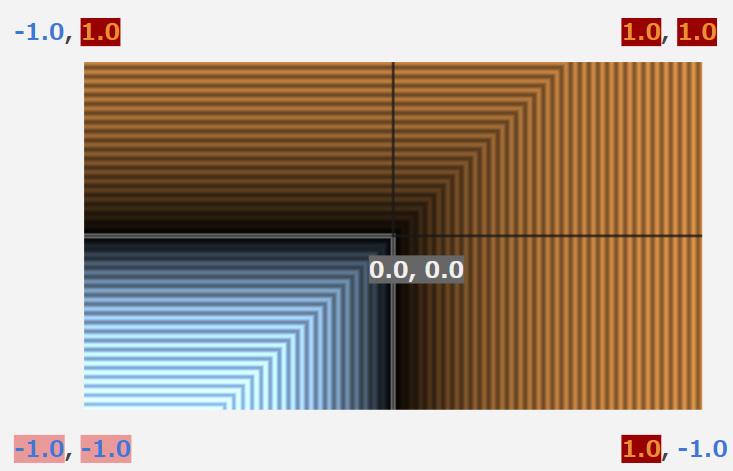
するとどういうことが起きるかというと、試しに円を八分割で複製して見比べてみます。

このように単純なy座標の移動のみだと、空間の切れ目にオブジェクトが移動してしまうので、見切れた形で複製されてしまいます。なので単純なy座標の移動のみを考えるだけで複製できるようにオフセットを追加する必要があります。
続いてこちらの部分
float n = pi2 / r;
a = floor(a/n)*n;
floorという関数が登場しましたが、これは床関数といって、小数点以下を切り捨てて整数部のみを残すという関数です。
先ほどatanで求めた、入力座標の角度を分割空間当たりの角度で割ったものを、さらにfloorで小数点を切り捨てると、空間毎のIDを求めることができます。
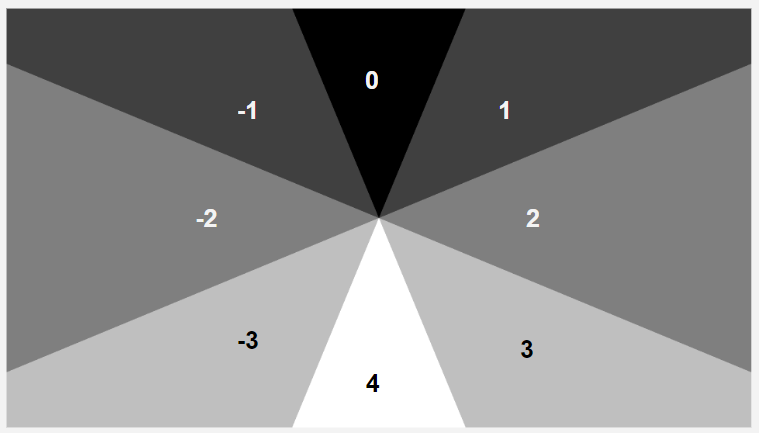
このIDに空間当たりの角度を掛けてやるとID0の空間と入力座標が属している空間の差分の角度がわかります。
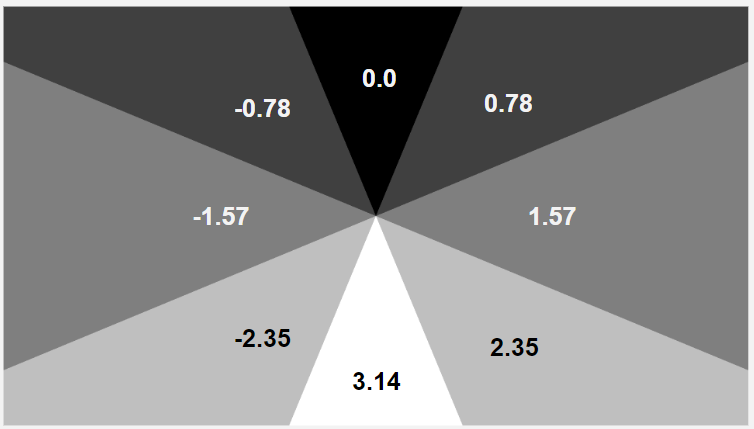
最後に、座標に対して、適した角度の回転をすることで、IDが0のエリア内のオブジェクトがその他のエリアにも現れて複製が完了します。
return p*rot(-a);
IFSによる複雑な形状
Iterated function systemを略してIFSといいます。
ループのイテレーションごとに、Foldや平行移動、回転などを座標に施して複雑なフラクタル形状を簡単に作成するテクニックです。
以下に箱に対してイテレーション毎に1回のFoldと2回の回転を行う簡単なIFSを適用した時の例を置いておきます。
for(int i=0; i<ITER; i++) {
p = abs(p) - 1.; // Fold
p.xz *= rot(1.); // 回転
p.xy *= rot(1.); // 回転
}
d = min(d, box(p));
X線のような見た目について
Phantom Mode
もしかしたらX線のような見た目になっていることに気づいた人がいるかもしれません。
この見た目はPhantom Modeと言うこれまた単純なテクニックで実現されています。
おそらくPhantom Modeの初出はaiekick先生のこちらのシェーダーだと思います。
https://www.shadertoy.com/view/MtScWW

簡単にやっていることを説明します。
このテクニックの肝はマーチングループにあります。
for(int i= 0;i < 99; i++) {
pos = ro + ray * t;
float d = map(pos);
d = max(abs(d), 0.02 + (exp(5.*sin(time * 0.3)) / exp(5.)) * 0.6);
ac += exp(-d * 3.);
gl += step(0.7, ii) * 0.3;
t += d * 0.5;
}
アニメーションのコードだったり無関係のところがあるので大事なところだけピックアップします。
このルックの肝はこの二行です。
d = max(abs(d), 0.02);
ac += exp(-d * 3.);
一行目はオブジェクトを透過させるための処理です。
この記事で距離関数は内部は負の距離になり、また限りなく0に距離近づいたら色を決定して早期終了すると説明しました。
実は今回のシェーダーではレイマーチング中の早期終了分岐が無くなっています。
最短距離の絶対値を取り、進む距離が絶対に0にならないように、今回だとmaxで0.02以下にならないようにすることで、レイがオブジェクトを突き抜けてforループが終わるまで進み続けます。
そして二行目は距離を適当な指数関数で減衰した値を密度としたボリューム累積を行っています。
↓はexp(-d*3.0)をプロットしたものです、距離関数で定義した輪郭付近(距離が0付近)が大きくなることがわかると思います。
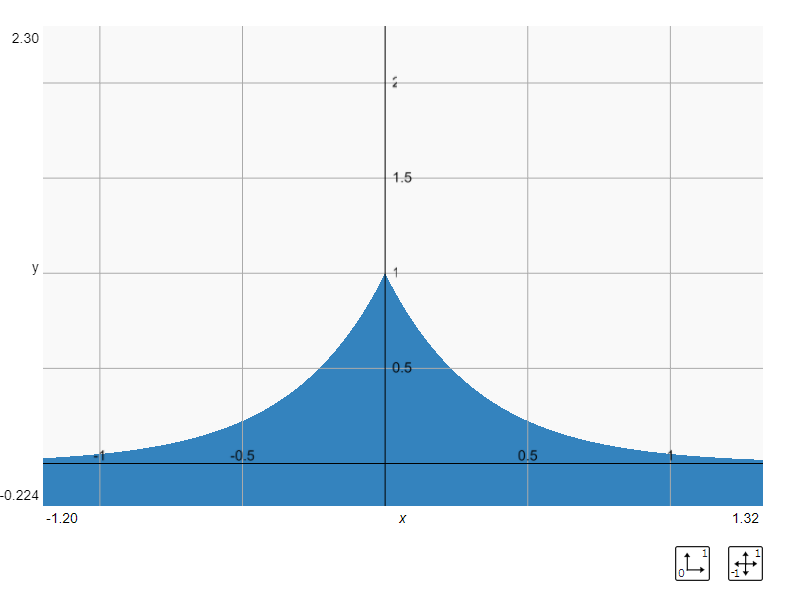
このボリュームを使って色付けをするとX線で写されたように透過感のあるルックになります。
今回のシェーダーのPhantom Modeに関連する箇所だけを抜き出した部分をこちらに置いておきます。
https://www.shadertoy.com/view/wl2GWG

HSV関数について
暗記していたHSVからRGBに変換するコードは@keim_at_si先生のこちらの記事のものです
丁寧な解説もありますし、コードがとにかく短いので、ある程度仕組みを理解しておけば丸暗記でなくても意外と実装できるようになりました!
魚眼レンズについて
vec3 ray = normalize(fo*((1.0-dot(p, p))*0.3 + 1.)+le*p.x+up*p.y);
この部分で魚眼っぽい効果を付けています。
肝はこちらの部分です。
((1.0-dot(p, p))*0.3 + 1.)
ここでスクリーン座標(~1~1)の距離の二乗でピクセル毎にfovを変更することで魚眼っぽい効果が生まれます。
@edo_m18先生のこちらの記事でさらに詳しく魚眼効果を解説してくださっています。
[GLSL] Shadertoyのシェーダ芸人になるためのTips集
まとめ
シェーダーライブコーディングがとても楽しいものだというのがこの記事を通してお伝えできていればうれしいです。
後半では、当日行ったライブコーディングで使用された重要なテクニックをいくつか紹介しました。
このように、この記事の内容をしっかり理解できていれば、少しのテクニックを追加するだけで魔法のように全然異なる見た目を作ることができます!
作る方も楽しいんですが、見る方もかなり楽しいので、この記事を読んで興味を持ってくれた方のライブコーディングが見れる時を楽しみにしています!!