[汎用関数]HSV2RGB 関数

#はじめに
「Shadertoy はじめました - Qiita」の子記事です。My First Shader Sound （※音が出ます）を作った際にいろいろ気づいたトピックスを小さめの記事にしていきたいと思います。
この記事では HSV 色空間から RGB 色空間への変換について説明します。前回に引き続きビジュアルプログラミングでよくあるネタですが、GLSLではベクトルを一括計算できたり、扱いやすいデフォルト関数があるので、非常にシンプルに計算できました（多分「車輪の再発明」だとは思うのですが、膨大な作品群から検索するよりも、自分で導出する方が早かった）。
Shaderとは直接関係のない話題ですが、「目的の形状のプロットを持つ数式を導出する」というプロセスは、オリジナルのシェーダアートを作る上で非常に重要な要素になると思います。曲線すら出てきませんので、普段から数式慣れしてる人には、かなり物足りない内容だと思います。

#いきなりファイナルアンサー
下式でh,s,v値からvec3型のRGB値が計算できます。

hsv2rgb.glsl

return ((clamp(abs(fract(h+vec3(0,2,1)/3.)*6.-3.)-1.,0.,1.)-1.)*s+1.)*v;

ちなみにWikipediaにもHSVをRGBに変換するサンプルコードが載っています。以下引用。

hsv2rgb.java

// (float h, float s, float v)
float r = v;
float g = v;
float b = v;
if (s > 0.0f) {
    h *= 6.0f;
    final int i = (int) h;
    final float f = h - (float) i;
    switch (i) {
        default:
        case 0:
            g *= 1 - s * (1 - f);
            b *= 1 - s;
            break;
        case 1:
            r *= 1 - s * f;
            b *= 1 - s;
            break;
        case 2:
            r *= 1 - s;
            b *= 1 - s * (1 - f);
            break;
        case 3:
            r *= 1 - s;
            g *= 1 - s * f;
            break;
        case 4:
            r *= 1 - s * (1 - f);
            g *= 1 - s;
            break;
        case 5:
            g *= 1 - s;
            b *= 1 - s * f;
            break;
    }
}

展開してみると同じ事をしているのですが、このコードと同じ計算を短い数式１つでできるというのは、純粋に美しいなーと思いました（小並感）。

#導出方法の解説
HSV色空間の詳しい説明についてはWikipediaに預けたいと思います。
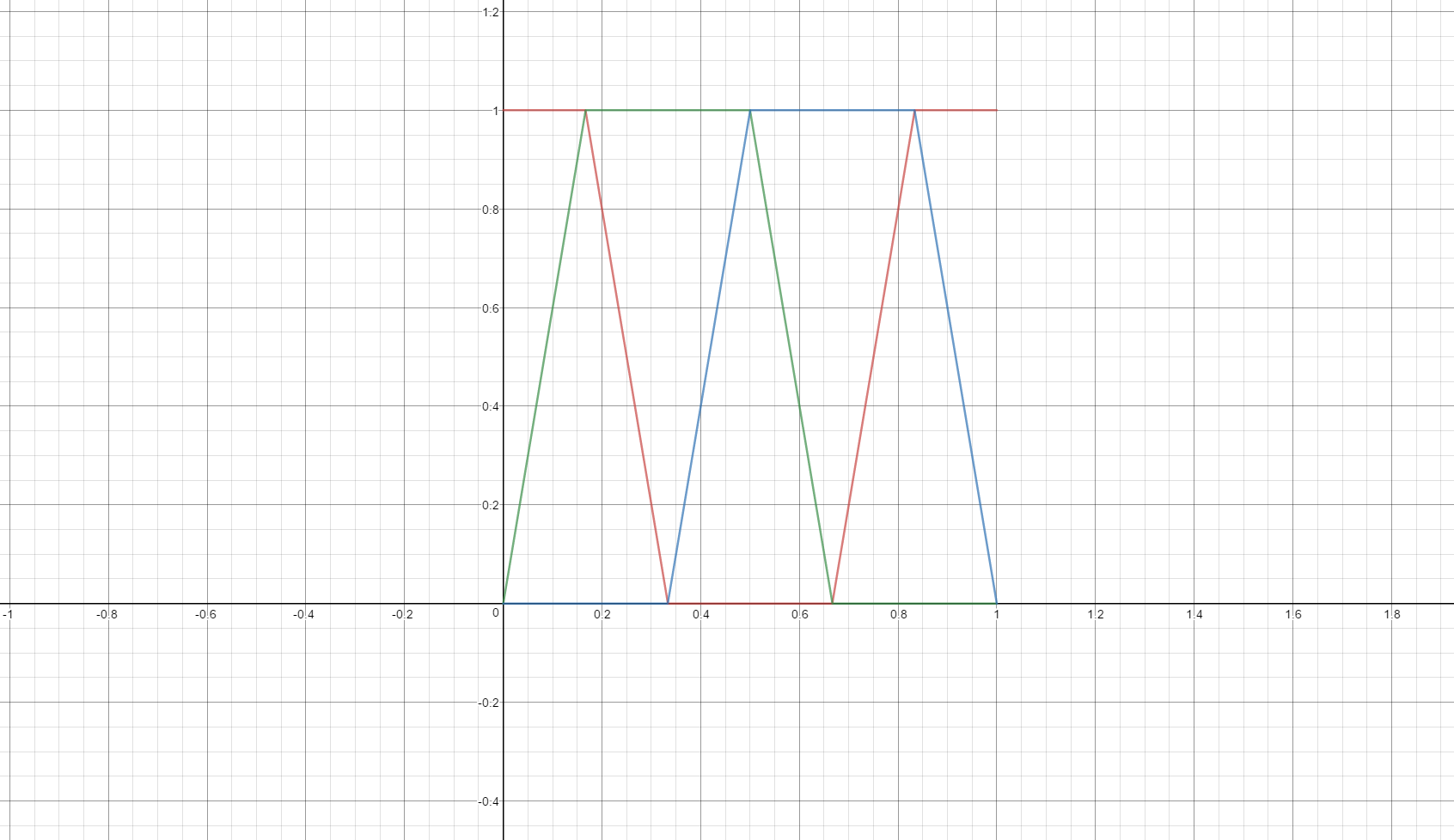
下図は$s=1,v=1$の条件で、$h$を横軸に取った場合のRGB各値のプロットです。

https://www.desmos.com/calculator/tyt51zahtx （リンク先では、s,vの値を操作できます。）

h(色相)の値によってR,G,B値が順番に入れ替わっている様子がわかると思います。
R値だけ抜き出すと下図のようなグラフになりますので、このグラフを数式で表現できれば良さそうです。

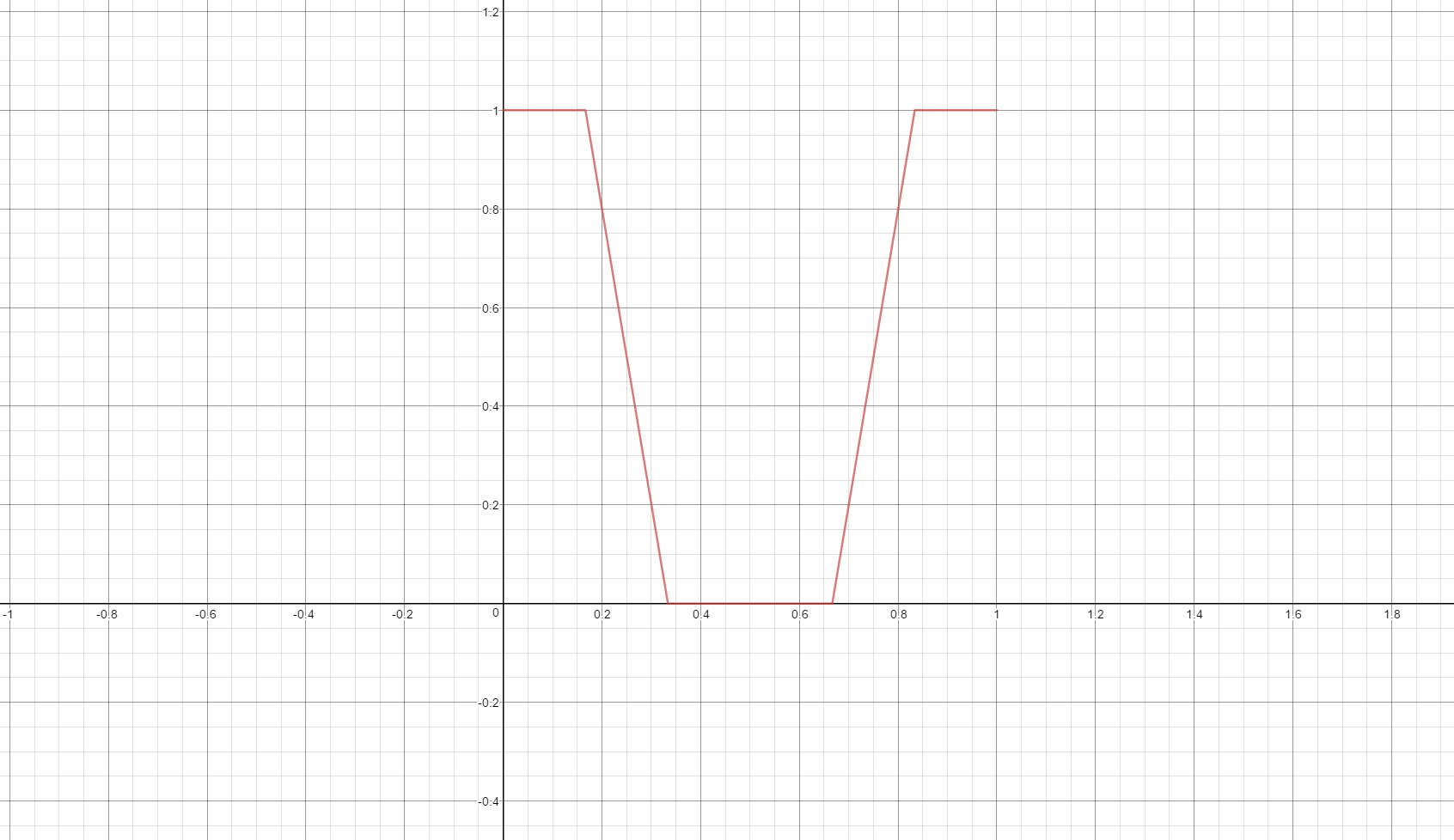
形状を見ると、0と1で頭打ち・底打ちしているのがわかります。**この頭打ち・底打ちはそれぞれmin・maxで表現できます。上下両方平たくする場合は、clampを用います。**上下に長いV字(下図青線)を0と1でclampすれば良さそうです。

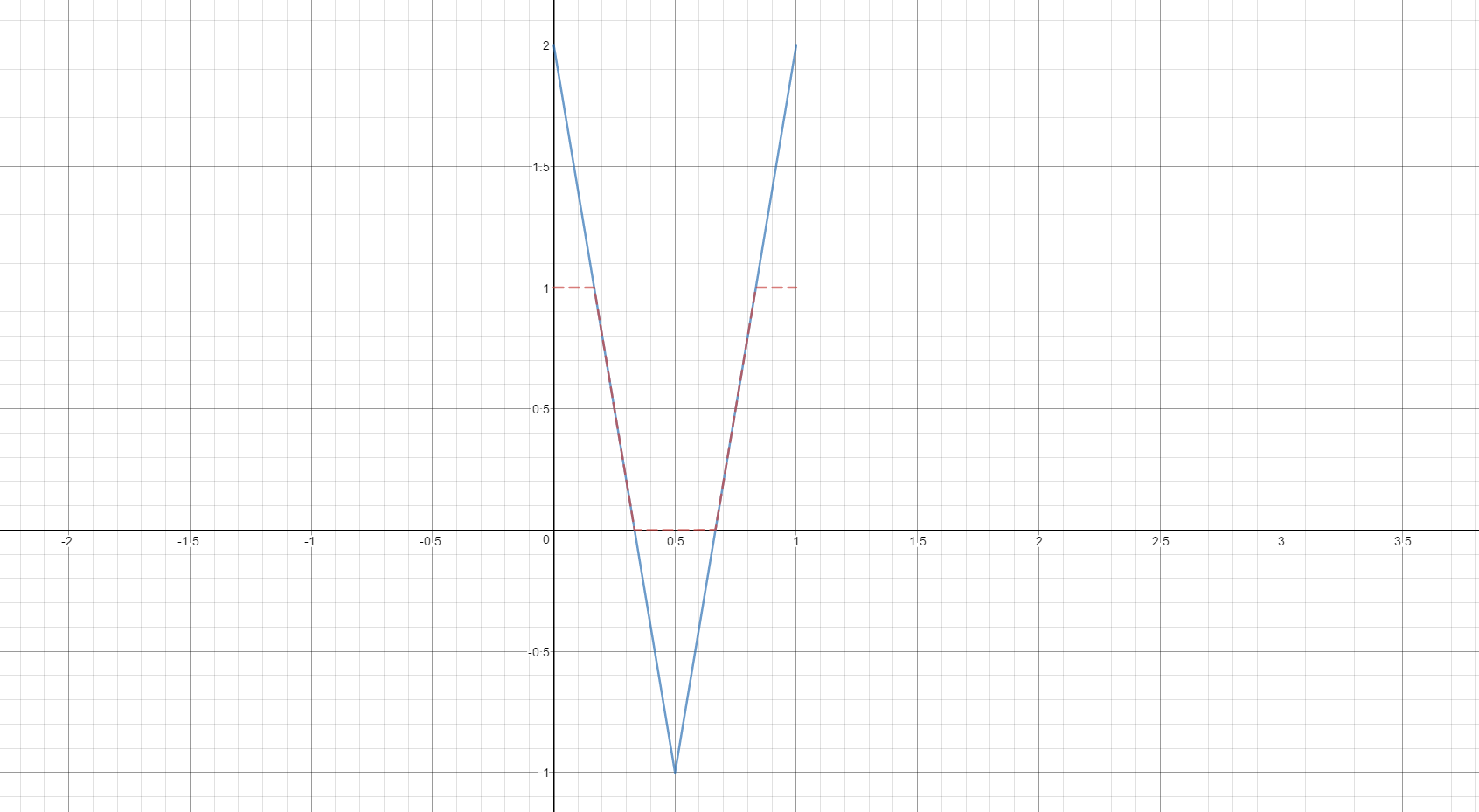
**絶対値を使うと0で折り返されるのでV字のグラフを作ることができます。**下図は、$|6x-3|$のプロットです。このプロットを -1 すれば y 軸下方向にプロットが 1 ずれますから、上図青線のV字が得られます。

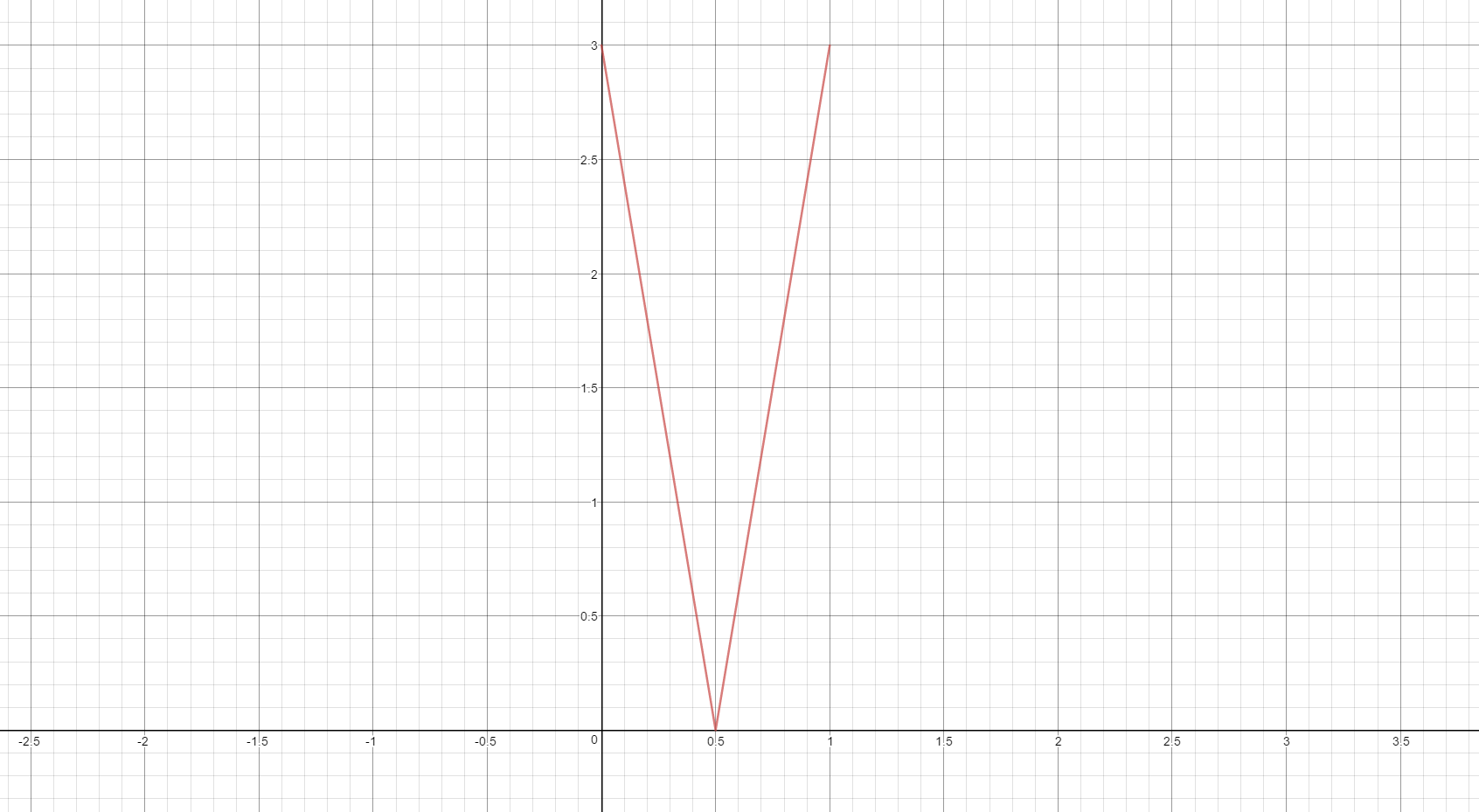
ここまでの流れで数式をつくると、最初の赤線の形状は $clamp(|6x-3|-1,0,1)$ という式になります。
一方、G 値と B 値は1/3ずつ h をずらせば得られますが、0-1の間でループしている必要があります。**0-1の間でループする場合はfract、任意の間でループさせる場合はmodが利用できます。**下図は $fract(x+2/3)$(緑線)、$fract(x+1/3)$(青線)のプロットです。

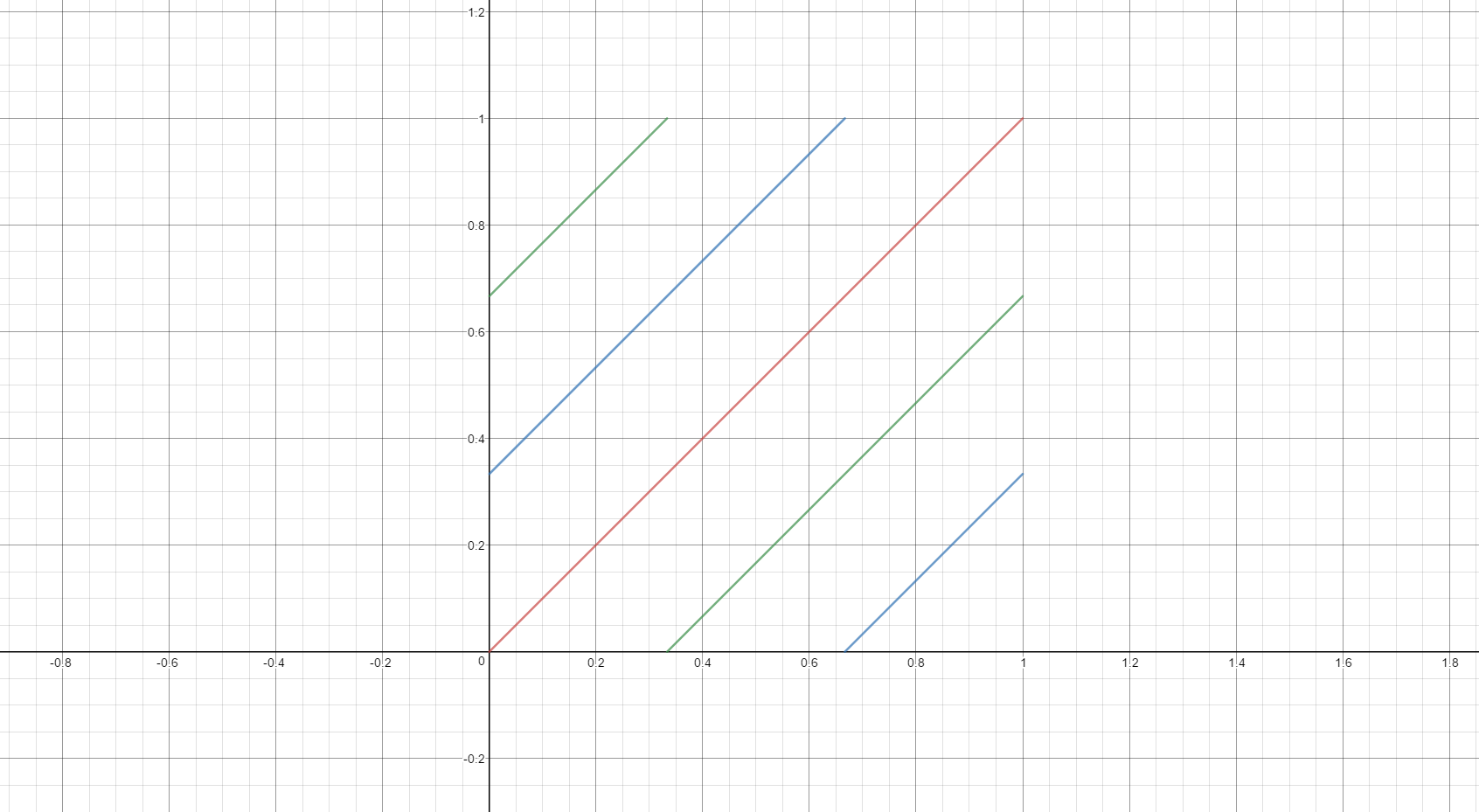
先ほどの赤線の数式のx値に、それぞれ緑青線の数式を代入すれば、h値からrgb値を計算することができるようになります。

clamp( abs(fract(h+vec3(0,2,1)/3) * 6 - 3) - 1, 0, 1)

s値とv値は、やり方を知っていればそれほど難しくありません。このページ で、s値を動かすと最大値固定で最小値が動くのがわかります。一方、v値は最小値固定で最大値が動きます。
最大値(=1として)固定で最小値を動かすような場合は、$(x-1)s+1$ と「1引いてから係数をかけて1を足す」計算をします。「負値にすることで係数が小さいほど最大値に近づくようにして、元に戻す」というイメージです。シェーダアートではかなり良く使う計算なので、毎度考えるより、そういうものと覚えてしまったほうが早いと思います。最小値固定の場合は、係数をかけるだけでOKです。
かくして、最初に示した関数が導出されました。

#感想
HSV→RGB 変換の関数だけ提示して終わろうと思ってたのですが、こういう「目的のプロットをもつ数式の導出」を細かく解説してるページって意外とないよなーと思ったので、細かめに解説してみました。
オリジナルの(コピペで済ませない)シェーダアートを作る場合、個人的に８割はこの「数式の導出」作業になるなーと感じています(数式慣れしている人ほど作業が早くなるので、相対的にこの割合は下がる気はします)。とはいえ、数学や物理の人たちが解くような数式の導出とはだいぶ違って、今回のようにパーツを組み合わせて目的のモノを作る感じになります。
物理的に正しい数式を真面目に解きたいような場合は、微分方程式の簡略化とか数学センスが問われる場面が多々ありそうですが、今回のようにそれっぽい数式の導出だけなら、パーツと利用法を知っているだけで、ほとんど数学はいらないと思います。
今後書こうとしている項目も、多くはこれら数式パーツに対する考察になると思いますし、今後自分もシェーダアートを作る過程で、色々な気づきがあると思います。それらをこの場で少しづつ共有していけたらと考えています。