[GLSL] Shadertoyのシェーダ芸人になるためのTips集

概要

今年はレイトレ、レイマーチング、レンダリングとシェーダ関連の勉強の優先順位を上げてやっていこうと思ってます。
ということで、色々とShadertoyでごにょごにょ実装中。

まだまだ全然知識不足ですが、色々な作品のコードを読み漁りつつ実装もしていこうかなと。
その中で見つけて、後々使えそうなこととかを細々とまとめていこうと思います。

なので見つけ次第随時更新な感じの記事です。

視点を歪める

これを知ったのはこちらの作品を見たときでした。
どういう見た目になるかは以下の動画を見てください。

• Menger Sponge Variation

▼ 歪んだ状態

▼ 通常の状態

だいぶ雰囲気が違うのが分かるかと思います。

さて、これを実現しているのが下記のところです。

// Unit direction ray vector: Note the absence of a divide term. I came across this via a comment 
// Shadertoy user "Coyote" made. I'm pretty happy with this.
vec3 rd = (vec3(2.0 * fragCoord - iResolution.xy, iResolution.y)); // Normalizing below.
    
// Barrel distortion. Looks interesting, but I like it because it fits more of the scene in.
// If you comment this out, make sure you normalize the line above.
rd = normalize(vec3(rd.xy, sqrt(max(rd.z * rd.z - dot(rd.xy, rd.xy) * 0.2, 0.0))));

いちおう、元になった投稿のコメントはそのまま残しています。

ここで行っている計算は、UVの値を元にカメラからのレイの方向を定める計算を行っています。
その際、Z方向（つまりいわゆる FocalLength）の計算を、UVの位置に応じて徐々に大きくなるように計算を行っているのがポイントです。
その部分を抜粋すると以下になります。

sqrt(max(rd.z * rd.z - dot(rd.xy, rd.xy) * 0.2, 0.0))

細かく分解すると以下。

float m = max(rd.z * rd.z - dot(rd.xy, rd.xy) * 0.2, 0.0);
sqrt(m);

最初の max 関数は、単純にマイナスになるのを防いでいるだけですね。
問題は rd.z * rd.z - dot(rd.xy, rd.xy) * 0.2 の部分。（ちなみに最後の * 0.2 は歪みを小さくするための補正）

rd.z の値は、ひとつ前の行で定義されていて、その値は iResolution.y の値が入っています。

これを2乗し、さらにそこから中心からの距離の2乗（dot(rd.xy, rd.xy)）の値を引いています。（距離は本来は平方根を取る必要があるので、計算的にはその2乗の値で計算を行っている）

この計算をマッピングしてみると以下のように「円」が現れます。

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    vec3 rd = vec3(fragCoord * 2.0 - iResolution.xy, iResolution.y);

    float m = sqrt(rd.z * rd.z) - sqrt(dot(rd.xy, rd.xy));
    
    vec3 col = vec3(m);

    fragColor = vec4(col,1.0);
}

このために、中心から徐々に歪んだ映像になる、というわけなんですね。

理屈としてはシンプルです。
rd.z * rd.z は高さの2乗ですね。しかし、その後に引く中心からの距離も2乗なのでここは2乗を無視して話を進めましょう。
また rd.xy の値は2倍されているので、中心から上端までの距離が iResolution.y と同じになります。

つまり、解像度の高さと同じ距離までは0以上の値が入り、それ以降はマイナスになります。
計算途中のものは解像度を元に計算しているためとても巨大です。（数千という値）
そのため、円の縁の際でやっと1以下の値が出てくる計算になります。

しかしシェーダはそもそも 0 〜 1 の範囲で色を決定するため、それ以上の値はクランプされて 1 とみなされます。
結果、上図のように円が表示される、というわけなんですね。

ランダム関数

まずは以下のThe Book of Shaderを読むと色々と情報が載っているのでおすすめです。

簡易的なランダム関数

上記のThe Book of Shaderでも紹介されていますが、簡単にノイズを生成する方法を紹介します。

sinとfractを用いた乱数

これを最初見たときは感動しました。
以下のように、 sin と fract だけを利用した簡易乱数です。

float rand(float x)
{
    return fract(sin(x) * 10000.0);
}

これを実行すると以下のようなランダムな状態が作れます。

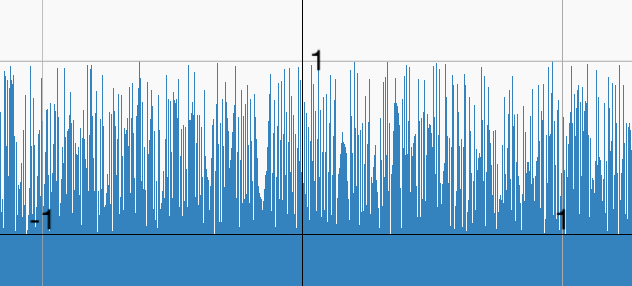
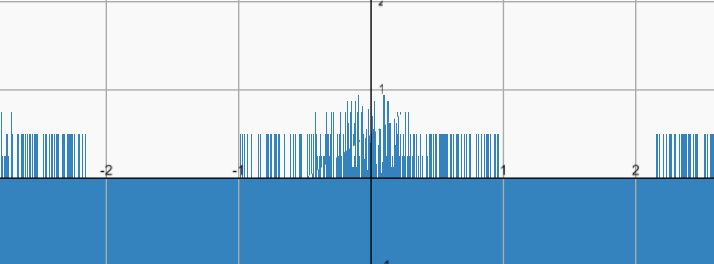
上記は、GLSL GrapherというサイトでGLSLの変化を可視化（グラフ化）したものです。

似たような結果をThe Book of Shaderのサイトでも実際にコードを修正しながらランダムに変化する様子を観察することができます。

dotとの組み合わせでvec2にも対応

上記は引数が float を受け取る関数でした。
これを、 vec2 （や vec3 ）に拡張したのが下の関数です。

float rand(vec2 st)
{
    return fract(sin(dot(st.xy, vec2(12.9898, 78.233))) * 10000.0);
}

よーく見てみると、最初の計算とほぼ同じことを行っているのが分かるかと思います。
vec2の場合には、なにか適当なベクトルとの内積を取ることでそれを float 化し、あとはその結果を使って前段の乱数生成関数と同様の計算を行えば、こちらもまた乱数を生成することができる、というわけです。

余談ですが、最後に掛けている 10000.0 をどんどん大きな値にしていくと結果が収束する、という点です。不思議。

10000000 倍するとこんな感じになります↓

バリューノイズ

比較的よく使われているノイズを紹介します。その名も「バリューノイズ」。
これは、空間をグリッドに区切って、そのそれぞれの頂点を利用した乱数を、さらにそのグリッドの小数部分を用いて補間を行った結果を利用したノイズです。

詳細はThe Book of Shaderに任せるとして、大まかなイメージは上記の通りです。

上記記事から引用させていただくと、2D版バリューノイズは以下のようになります。

// 2D Random
float random (in vec2 st) {
    return fract(sin(dot(st.xy,
                         vec2(12.9898,78.233)))
                 * 43758.5453123);
}

// 2D Noise based on Morgan McGuire @morgan3d
// https://www.shadertoy.com/view/4dS3Wd
float noise (in vec2 st) {
    vec2 i = floor(st);
    vec2 f = fract(st);

    // Four corners in 2D of a tile
    float a = random(i);
    float b = random(i + vec2(1.0, 0.0));
    float c = random(i + vec2(0.0, 1.0));
    float d = random(i + vec2(1.0, 1.0));

    // Smooth Interpolation

    // Cubic Hermine Curve.  Same as SmoothStep()
    vec2 u = f*f*(3.0-2.0*f);
    // u = smoothstep(0.,1.,f);

    // Mix 4 coorners percentages
    return mix(a, b, u.x) + // 左上から右上の頂点への補間
              (c - a)* u.y * (1.0 - u.x) + // 左上から左下への補間
              (d - b) * u.x * u.y; // 右上から右下への補間
}

ここの乱数生成でも、冒頭の sin と fract を利用した関数が使われているのが分かりますね。

これを3D版に拡張すると以下のようになります。

float hash(vec2 n)
{
    return fract(sin(dot(n, vec2(123.0, 458.0))) * 43758.5453);
}

float noise(in vec3 x)
{
    vec3 p = floor(x);
    vec3 t = fract(x);

    t = t * t * (3.0 - 2.0 * t);

    float n = p.x + p.y * 57.0 + 113.0 * p.z;
    
    float a = hash(n +   0.0);
    float b = hash(n +   1.0);
    float c = hash(n +  57.0);
    float d = hash(n +  58.0);
    float e = hash(n + 113.0);
    float f = hash(n + 114.0);
    float g = hash(n + 170.0);
    float h = hash(n + 171.0);
    
    float m1 = mix(a, b, t.x);
    float m2 = mix(c, d, t.x);
    float m3 = mix(e, f, t.x);
    float m4 = mix(g, h, t.x);
    
    float m5 = mix(m1, m2, t.y);
    float m6 = mix(m3, m4, t.y);
    
    float res = mix(m5, m6, t.z);
    
    return res;
}

見比べてみると、基本的な考え方は変わっていないのが分かるかと思います。

これを使うには以下のようにします。

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    vec2 uv = (fragCoord * 2.0 - iResolution.xy) / iResolution.y;

    // ノイズのスケールを変更する（UV値が100倍されるので見た目は縮小する）
    uv *= 100.0;
    
    float n = noise(uv);
    
    // 得られたfloat値を使って色を決定する（グレースケールのノイズ）
    vec3 col = vec3(n);

    fragColor = vec4(col, 1.0);
}

実行するとこんな感じになります。

グリッドを描く

グリッドは、ランダム関数のところでも触れた、fract を使って描きます。
（余談ですがこの fract ってフラクタルから作られた関数名ですかね）
コメントで指摘もらいましたが fractional（分数）が元ですね。

まずざっくりとコードを。

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    // Canvasのサイズを-1 ～ 1に変換する
    vec2 uv = (fragCoord - 0.5 * iResolution.xy) / iResolution.y;

    uv *= 5.0; // UV値のスケールを変更する

    vec2 gv = fract(uv);

    vec3 col = vec3(0);

    if (gv.x > 0.98 || gv.y > 0.98) col = vec3(1, 0, 0);

    fragColor = vec4(col, 1.0);
}

やっていることは乱数のときと同様に、UV を適当な倍数を掛けてスケールさせ、その値を fract によって 0.0 ~ 1.0 の間で繰り返させます。

そしてその値の境目を検知して色を付ける、という具合です。
色を付けているのは以下の部分ですね。

if (gv.x > 0.98 || gv.y > 0.98) col = vec3(1, 0, 0);

これを実行すると以下のようにグリッドが表示されます。

UV のスケールを変更してやればもっと細かくなったり、あるいは逆に拡大されたりします。

グリッドのID（位置）計算

色々な投稿を見ているとわりとよく見るやつです。

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    vec2 uv = (fragCoord * 2.0 - iResolution.xy) / iResolution.y;

    uv *= 5.0;

    vec2 id = floor(uv);
    vec2 f = fract(uv);

    vec2 c = id * 0.2 * 0.5 + 0.5;
    vec3 col = vec3(c, 0.0);

    // if (f.x > 0.98 || f.y > 0.98) col += vec3(1.0, 0.0, 0.0);

    fragColor = vec4(col, 1.0);
}

ポイントは vec2 id = floor(uv); としているところですね。
floor は整数部分を返してくれる関数です。
（ちなみにfloor、フロア、つまり各階層ごとってことで整数だけを返す関数名として使われているのかなと思いました）

つまり fract とちょうど逆の処理、と考えてもいいと思います。
fract は小数部分だけを返し、floor は整数部分だけを返す。

上記のコードを実行すると以下のようなグリッド状の絵が描かれます。

モザイクエフェクトもこの floor を使って実現しているのでそう考えながら見るとモザイクにも見えてきたりします。

stepの活用法

Shadertoyのコードリーディングをしているとたまに見かける step による表現。
特にGPUプログラムは if 文による分岐が苦手（重い）ので、step 関数によって if 文ライクな書き方をしているのも少なくありません。

【コメントによる指摘】
コメントで以下の指摘をいただきました。

単なる式なら、abs(sign(x - edge))のように変にトリックを使うよりもint(x != edge)のように素直に条件式を使ってキャストしたほうが速いですよ。手元の環境(GeForce + Unity ComputeShader)でストレステストも行ってみましたがやはり後者のほうが負荷が軽かったです。

このコメントに返信する形でGPUが条件分岐が苦手な理由を書いていますが、それゆえにstepの使い道として負荷軽減のためと書いていましたが、もしかしたら短く書くというShadertoyの文化による書き方かもしれません。

ただ、じゃあなにがどうなっているのか、というのを理解しておくのは有意義だと思うので以下にメモとして残しておこうと思います。

なお、詳細についてはこちらの記事を参考にさせていただきました。

• 条件分岐のためにstep関数を使う時の考え方をまとめてみた

まず、 step 関数の役割ですが、ドキュメントを見ると以下のように書かれています。

genType step(genType edge, genType x);
genType step(float edge, genType x);

step generates a step function by comparing x to edge.
For element i of the return value, 0.0 is returned if x[i] < edge[i], and 1.0 is returned otherwise.

つまり、 edge で与えられた値と x の値を比較し、その境界をまたいで 0.0 か 1.0 を返してくれる（二値化してくれる）関数、ということですね。（ edge より下なら 0.0、 edge 以上なら 1.0 を返してくれる）

そして参考にさせてもらった記事から引用すると、以下のような感じで if 文を消すことができるようになります。

vec3 BLACK = vec3(0.0);
vec3 WHITE = vec3(1.0);

vec3 color;

// なにがしかの評価したいベクトル
vec3 x = vec3(0.4, 0.5, 0.6);

// 判定したい境界
vec3 edge = vec2(0.5);

// step(edge, x)を実行すると、
// .xは 0.4 < 0.5 なので 0.0
// .yは 0.5 >= 0.5 なので 1.0
// .zは 0.6 >= 0.5 なので 1.0
// 結果、vec3(1.0, 0.0, 0.0)というベクトルになる

// そしてその結果をmixの第3引数にすることで、
// 第1引数と第2引数に対するマスク的な役割を果たす
color = mix(WHITE, BLACK, step(edge, x));

x != edge

// x != edge なら 1.0
abs(sign(x - edge));

x == edge

// x == edge なら 1.0
vec4(1.0) - abs(sign(x - edge));

Tips系

コアな仕組みとは別の、Tips的な小粒なやつをまとめていきます。

Cameraの姿勢制御

レイマーチングをするとき、カメラの姿勢を外積を使ったりして求めたりしますが、関数にして行列を返すようにするとレイマーチングの本体側のコードがシンプルになるので、コードスニペットとしてメモ。

やっていることは、カメラの姿勢を表すx, y, z軸の方向を求めてそれを行列にして返しているだけです。
たまにShadertoyのコードの中で似た形のもので実装されているものがあるので覚えておくとコードが読みやすくなると思います。

///
/// カメラの姿勢行列を生成する
///
/// ro = Ray origin
/// ta = Target
mat3 camera(vec3 ro, vec3 ta)
{
    // カメラのforward
    vec3 cw = normalize(ta - ro);
    // ひとまずの計算用のup方向ベクトル
    vec3 cp = vec3(0.0, 1.0, 0.0);
    // カメラの横ベクトル
    vec3 cu = cross(cw, cp);
    // カメラの上ベクトル
    vec3 cv = cross(cu, cw);
    // それぞれのベクトルを行列の要素にして返す
    return mat3(cu, cv, cw);
}

// ...

// 使い方
vec3 ta = vec3(0.0, 0.0, 0.0);
vec3 ro = vec3(0.0, 0.0, 2.0);
    
mat3 c = camera(ro, ta);
    
// focalLength
float fl = 1.3;
vec3 dir = c * normalize(vec3(uv, fl)); // これで、カメラから見たテクセルへのレイの方向が求まる

ガンマ補正

Wikipediaから引用させてもらうと以下のように書かれています。

ガンマ値（ガンマち）とは、画像の階調の応答特性を示す数値。また、入出力機器のガンマ値に応じた最適のカーブに画像の階調を補正することをガンマ補正（ガンマほせい）という。

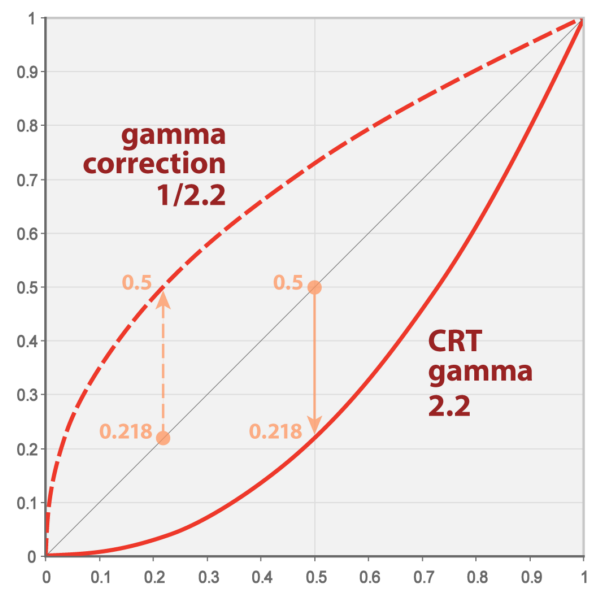
また、同様にWikipediaから引用させてもらうと、どういう補正が行われるのかは以下の図ようになります。

つまり、$\frac{1}{2.2}$乗することで、元の線形の値へと戻す、ということですね。
そして$\frac{1}{2.2} = 0.4545454545$なので、簡易的に0.4545を用いることにして、以下のように最終的な色の結果をさらにpow関数によって補正してやることで、リニア空間での色が表現できる、というわけです。
（Shadertoyでこれを行っている場合はガンマ補正をしていると考えていいと思います）

vec3 col = /* get color */;
col = pow(col, vec3(0.4545)); // => 色の1/2.2乗

法線計算

続いて法線計算。
レイマーチングでオブジェクトをレンダリングする場合、ライティングなどの関係で法線を求めるのは必須に近いです。
法線の求め方は簡単で、法線を求めたいレイの位置を引数にして、x, y, z軸それぞれの偏微分を取ってそれを正規化したベクトルが法線となります。

ちなみになぜ偏微分で法線が求まるのか、ということに関しては以前にちょっとした記事を書いたので興味がある方は読んでみてください。

• 偏微分（勾配）が法線を表すイメージ

vec3 getNormal2(vec3 p)
{
    const float eps = 0.001;
    vec2 e = vec2(eps, 0);
    
    return normalize(
        vec3(sp_dist(p + e.xyy) - sp_dist(p - e.xyy),
             sp_dist(p + e.yxy) - sp_dist(p - e.yxy),
             sp_dist(p + e.yyx) - sp_dist(p - e.yyx)));
            
}

簡易法線計算

iqさん？が考案した簡易法線計算方法。
上記の計算をある程度端折って、ある程度それっぽい法線を求める計算方法です。

ただ、実際に計算してみて微妙に結果が異なったので、あくまで計算負荷が高くそれを軽減したい場合に使う、くらいのほうがいいかもしれません。

vec3 getNormal(vec3 p)
{
    const float eps = 0.001;
    vec2 e = vec2(1.0, -1.0) * 0.5773 * eps;

    return normalize(e.xyy * map(p + e.xyy) +
                     e.yyx * map(p + e.yyx) + 
                     e.yxy * map(p + e.yxy) +
                     e.xxx * map(p + e.xxx));
}