はじめに
求人検索サービスを提供する株式会社スタンバイでデータアナリスト兼エンジニアとして
データ分析やスタンバイの施策におけるデータ活用の支援をしている小池です。
今年の漢字は「税」でしたね。
インボイス制度をはじめとして税の話題に事欠かない一年だったと思います。
私にとっては税金だけにとどまらない、マネーリテラシー全般を高めるモチベーション
爆上がりっぱなしな一年でした。
あと、2024年明けからのNISA神改良に興奮して夜も眠れないw今日この頃です。
ちなみに本日はクリスマスイブ![]() 、何と言っても私の誕生日
、何と言っても私の誕生日![]() と結婚記念日
と結婚記念日![]() です。
です。
こんなめでたい日にアドベントカレンダー執筆を担当させていただき森羅万象に感謝です。
スタンバイ Advent Calendar 2023の24日目の記事として、去る2023年11月19日(日)に
統計検定1級を受験してきたのでその戦いの記録その他諸々を書きたいと思います
統計検定とは
公式ホームページによれば
統計に関する知識や活用力を評価する全国統一試験です。
データに基づいて客観的に判断し、科学的に問題を解決する能力は
仕事や研究をするための21世紀型スキルとして国際社会で広く認められています。
日本統計学会は、国際通用性のある統計活用能力の体系的な評価システムとして
統計検定を開発し、様々な水準と内容で統計活用力を認定しています。
です。統計のスキルを5段階(4級、3級、2級、準1級、1級)で証明する検定と認識していただければ大丈夫かと思います。各級の内容についてはこちらを御覧ください。
最近では企業におけるデータサイエンティストの求人要件として挙げられるケースも出始めており、例えば、ファーストリテイリング社では、必須要件として2級相当、歓迎要件として準1級相当を掲げているといった事例もあります。
今回私が受験した1級は、統計数理と統計応用(人文科学、社会科学、理工学、医薬生物学の中から受験申し込み時に1分野選択)の2つの試験に合格する必要があり、他の級がCBT対応して一年中受験可能かつ選択解答式という仕様になる中、頑なまでに完全記述式、受験機会年1回を貫くなど、統計検定のラスボスにふさわしい鬼仕様です。(統計数理と統計応用のどちらか片方合格の場合、合格した試験に関しては10年間免除される事が唯一の救い)
なぜ1級を取ろうと思ったか
こちらの仕事で対数正規分布と最尤法を使う機会があり、現象を簡潔に表現する言語としての素晴らしさに改めて気づき、数理的な観点から統計をしっかり理解したいと思った事と、自身が統計を使えるシーンがとても限定的だったので、午後の統計応用の学習を通じてもっと活用できる幅を広げたかった事が受験のきっかけです。
余談ですが、当初は統計応用は社会科学か人文科学の選択を検討していました。
(アンケートの設計や分析の話など、勉強したことを仕事に還元しやすいと考えたため)
しかし、そんな志も受験日が近づくに従って、不慣れな分野での学習に心が折れ
申し込みの際はなんの迷いもなく「理工学」を選択していました。
戦いの記録
2022年11月〜12月(本番12ヶ月前〜11ヶ月前)
はじめに申し上げておくと、私は釣りが(自分で捌いて調理も)好きで
月1〜2のペースで相模湾か東京湾に繰り出している。
この日も秋の相模湾でいつものように釣りを楽しんでいる時だった。
ふと、「そうだ、統計学をまじ基本的なところから学び直そう」と思い立ち、
帰宅途中に立ち寄った書店で演習 統計学 キャンパス・ゼミを購入し
1ヶ月くらいで一気に仕上げた。
この学習成果が前述の仕事に繋がり
「どうせなら統計検定1級とってやろう、1年あればなんとかなるっしょ」
とテンション爆上がりのまま年末を迎えた。
↓は、この頃に生涯で初めて釣り上げたわらさ
(ぶりの若魚、成長とともに関東ではわかし→いなだ→わらさ→ぶり、と名前が変わる)
お造りとぶり大根が美味でした。

2023年1月〜3月(本番10ヶ月前〜8ヶ月前)
年明け早々、まだお屠蘇気分も抜けきらぬうちに統計検定1級対応 統計学を読み始めるも
全く理解できず、心バッキバキに折れかかる。
おまけに年度末で仕事で怒涛の日々が続き、昨年末のテンションも敢え無く降下。全く進捗せず。
なお、学習の進捗とは裏腹に釣りの方は好調で、
↓は、この時期に生涯で初めて釣り上げた真鯛、お造りと煮付け、鯛出汁茶漬けが美味でした。
2023年4月〜5月(本番7ヶ月前〜6ヶ月前)
統計検定1級受験者のブログで現代数理統計学の基礎という1級受けるなら読んどけくらいの定番書籍の存在を知り購入、興味の赴くままにつまみ読みしてた。
この時期はまだ、過去問勉強法などという単に合格を目的とした勉強法に頼りたくないと余裕ぶっこいていた。
↓は、この時期に生涯で初めて釣り上げた目鯛(めだい)、幽庵焼きが美味でした。
2023年6月〜9月(本番5ヶ月前〜2ヶ月前)
本番まで半年を切り背に腹は代えられないと思い、過去問勉強法を通じて内容の理解と本番での答案作成力を同時に磨く作戦に切り替える。この頃はひたすら公式問題集をやっていた。
また、この頃に統計応用を理工学で受験することを決意。
この頃は、あまり目立った釣果がなかった。
2023年10月〜11月(本番1ヶ月前〜0ヶ月前)
ホームページから受験申し込み完了。11月初旬に受験票が届く。受験会場は学習院大学(目白キャンパス)。試験当日は山手線が渋谷駅工事のため終日内回りが運休との事で、帰りが大変そう、ということを受験票が届いて知る。早くも暗雲立ち込める。
2023年11月11日(土)(本番1週間前)
気分転換に茅ヶ崎沖に釣りに行く。8kgオーバーのぶりを釣り上げ、
「来週の統計検定もいけるんじゃね」などと根拠の無い自信をもつ。
なお、翌日からしばらく食卓にぶりが振る舞われた事は言うまでもない。
(お造り、ブリしゃぶ、塩焼き、てりやき、ぶり大根が美味でした。)
↓は釣り上げた直後のぶり。
↓は↑の調理直前のぶりと餌のサバとのツーショット。
テーブルが汚れないように空き牛乳パックを敷いている。

2023年11月19日(日)(本番当日)
試験本番当日。午前の統計数理、午後の統計応用(理工学)ともに90分間で5問から3問を選択して回答。回答の記述に大苦戦する。過剰に丁寧に書きすぎているんじゃないか、もっと効率の良い解き方や答案の書き方があるんじゃないか、という迷いを抱えながら、あっという間に試験時間が過ぎ去る。半分も回答出来たか怪しい。
試験終了後の帰り道、「昨年よりは手応えあったわ〜」という他の受験生の声を聞く。合格率20%程度の試験、やはり一発での合格は難しいようだ。
2023年11月23日(木)(本番4日後)
特に受かった実感も無いが、頑張ってきた自分へのご褒美に、
5回めのコロナワクチン接種後、翔んで埼玉 〜琵琶湖より愛をこめて〜を公開初日に鑑賞。
(これが楽しみ過ぎて前日ほとんど寝れなかった)
バカバカしい事をど真剣にやっている姿は人に深い感動と心からの笑いを与えるのだと学んだ。
来年こそはこの映画に負けないくらいど真剣に取り組もうと思う。
統計検定の数学
これで終わってしまうと単なる釣果報告、失礼、敗戦報告になってしまい、記事としては少々寂しいので以下学習を進める上で特に大事だと思った数学的な内容について解説したい。
統計学は応用数学の1分野である。そのため、過去問解説書をはじめ多くの書籍が高校(理系コース、いわゆる数Ⅲ・Cを履修)〜大学教養レベルの知識を前提として書かれており、数学(特に微積分、線形代数)の習熟度合いが学習しやすさを大きく左右する。
特に、統計検定1級の統計数理は微積分、線形代数を始めとする数学の総合格闘技、統計応用に至っては更に各専門分野固有の手法(理工学分野であれば例えば、中心複合計画、管理図など)が加わる。数学にアレルギーのある方が事前の対策無しに勉強を始めるとアナフィラキシーで泡吹いてしまうことだろう。
ただ、そのために高校数学や大学教養の微積分、線形代数をいちから勉強するのは、つみたてNISAで資産形成を始めるのに一◯大学に入学して経済学や現代ポートフォリオ理論を勉強するのと同じくらい遠回りかと思う。
そこで本記事では、統計検定1級で比較的よく出題される内容を題材として、特に押さえておきたいアイテムを厳選して紹介する。解説書だと省略されるような計算過程についてもできるだけ詳細に記述したつもりなので、学習の参考になれば幸いだ。
期待値、分散を求める
与えられた確率密度関数(確率変数が連続値の場合)や確率関数(確率変数が離散値の場合)をもとに、確率変数の期待値や分散を求める問題。ここで連続値とは身長や体重といった連続な値、離散値とはサイコロの目といった飛び飛びの値である。
計算の流れは次の通り。
- 確率変数の期待値$(E[X])$を求める
- 確率変数の2乗の期待値$(E[X^2])$を求める
- 1., 2.の結果と分散と期待値の関係式$V[X] = E[X^2] - (E[X])^2$を使って分散を求める
ここでは、
極限、微分、部分積分、広義積分、無限級数和、テイラー展開(マクローリン展開)
の知識が必要となる。以下に例を示す。
例1:確率変数$X$が連続値の場合
確率変数$X$が正規分布$N(\mu, \sigma^{2})$に従う場合の確率変数$X$の期待値$E[X]$及び分散$V[X]$をもとめる。まず、期待値$E[X]$について、期待値の定義により
\begin{align}
E[X] = \int_{-\infty}^\infty xf(x)dx = \int_{-\infty}^\infty x\frac{1}{\sqrt{2\pi\sigma^{2}}} exp\lbrace -\frac{(x - \mu)^{2}}{2\sigma^{2}} \rbracedx
\end{align}
ここで、前述の式の$exp$の中身に着目し、
\frac{(x - \mu)^{2}}{2\sigma^{2}} = \frac{1}{2} (\frac{x - \mu}{\sigma})^{2}
より
x^{\prime} = \frac{x - \mu}{\sigma}
として両辺を$x$で微分すると
dx^{\prime} = \frac{1}{\sigma}dx \Rightarrow \sigma dx^{\prime} = dx
であるから、
E[X] = \int_{-\infty}^\infty (\sigma x^{\prime} + \mu)\frac{1}{\sqrt{2\pi\sigma^{2}}} exp\lbrace -\frac{(x^{\prime})^{2}}{2} \rbrace \sigma dx^{\prime}
= \frac{\sigma}{\sqrt{2\pi}}\int_{-\infty}^\infty x^{\prime} exp\lbrace -\frac{(x^{\prime})^{2}}{2} \rbrace dx^{\prime} + \mu \int_{-\infty}^\infty\frac{1}{\sqrt{2\pi}} exp\lbrace -\frac{(x^{\prime})^{2}}{2} \rbrace dx^{\prime}
= \frac{\sigma}{\sqrt{2\pi}} [-exp\lbrace -\frac{(x^{\prime})^{2}}{2}\rbrace]_{-\infty}^{\infty} + \mu \int_{-\infty}^\infty\frac{1}{\sqrt{2\pi}} exp\lbrace -\frac{(x^{\prime})^{2}}{2} \rbrace dx^{\prime}
ここで第1項は
\lim_{x^{\prime} \to \pm\infty} exp\lbrace -\frac{(x^{\prime})^{2}}{2}\rbrace = 0
より$0$となり、第2項の積分は標準正規分布$N(0,1)$の確率密度関数の全区間での積分であるから
\int_{-\infty}^\infty\frac{1}{\sqrt{2\pi}} exp\lbrace -\frac{(x^{\prime})^{2}}{2} \rbrace dx^{\prime} = 1
したがって、確率変数$X$の期待値$E[X]$は
E[X] = \mu
次に、分散$V[X]$を求める。分散と期待値の関係式
V[X] = E[X^2] - (E[X])^2
より、あとは$E[X^2]$が求められれば$V[X]$が求められるので、$E[X^2]$を求める。
E[X^2] = \int_{-\infty}^\infty x^2f(x)dx = \int_{-\infty}^\infty x^2\frac{1}{\sqrt{2\pi\sigma^{2}}} exp\lbrace -\frac{(x - \mu)^{2}}{2\sigma^{2}} \rbracedx
= \int_{-\infty}^\infty (\sigma x^{\prime} + \mu)^{2}\frac{1}{\sqrt{2\pi\sigma^{2}}} exp\lbrace -\frac{(x^{\prime})^{2}}{2} \rbrace \sigma dx^{\prime}
= \sigma^2\int_{-\infty}^\infty x^{\prime 2} \frac{1}{\sqrt{2\pi\sigma^{2}}} exp\lbrace -\frac{(x^{\prime})^{2}}{2} \rbrace \sigma dx^{\prime}
+ 2\sigma \mu \int_{-\infty}^\infty x^{\prime}\frac{1}{\sqrt{2\pi\sigma^{2}}} exp\lbrace -\frac{(x^{\prime})^{2}}{2} \rbrace \sigma dx^{\prime}
+ \mu^{2} \int_{-\infty}^\infty \frac{1}{\sqrt{2\pi\sigma^{2}}} exp\lbrace -\frac{(x^{\prime})^{2}}{2} \rbrace \sigma dx^{\prime}
= \sigma^{2} + \mu^{2}
したがって、確率変数$X$の分散$V[X]$は
V[X] = E[X^2] - (E[X])^2 = \sigma^{2} + \mu^{2} - \mu^{2} = \sigma^{2}
と求められる。
例2:確率変数$X$が離散値の場合
整数値をとる確率変数$X$がパラメータ$\lambda$のポアソン分布
Po(\lambda) = \frac{\lambda^x}{x!}e^{-\lambda}
に従う場合の確率変数$X$の期待値$E[X]$及び分散$V[X]$をもとめる
まず、確率母関数$G(s)$求めておく。
G(s) = E[s^x] = \sum_{x = 0}^{\infty} s^x Po(\lambda)
= \sum_{x = 0}^{\infty} s^x \frac{\lambda^x}{x!}e^{-\lambda} = e^{-\lambda}\sum_{x = 0}^{\infty} \frac{(s\lambda)^x}{x!}
ここで、$e^{\lambda}$のマクローリン展開を考えると
e^{\lambda} = 1 + \frac{\lambda}{1!} + \frac{\lambda^2}{2!} + \frac{\lambda^3}{3!} + \cdots = \sum_{x=0}^{\infty}\frac{\lambda^x}{x!}
であるから、この式において$\lambda \rightarrow s\lambda$とすると
e^{s\lambda} = 1 + \frac{s\lambda}{1!} + \frac{(s\lambda)^2}{2!} + \frac{(s\lambda)^3}{3!} + \cdots = \sum_{x=0}^{\infty}\frac{(s\lambda)^x}{x!}
であることから、求める確率母関数$G(s)$は、
G(s) = e^{-\lambda} \cdot e^{s\lambda} = exp[\lambda(s-1)]
ここで確率母関数の変数$s$についての1階導関数を求めると
G^{\prime}(s) = E[xs^{x-1}] = \lambda exp[\lambda (s - 1)]
となり、ここで$s=1$とおくと
G^{\prime}(1) = E[X] = \lambda
であることから、期待値は
E[X] = \lambda
と求められる。
次に分散$V[X]$について、
V[X] = E[X^2] - (E[X])^2 = E[X^2] - E[X] + E[X] - (E[X])^2
= E[X^2 - X] + E[X] - (E[X])^2 = E[X(X-1)] + E[X] - (E[X])^2
ここで、確率母関数$G(s)$の2階導関数を求めると
G^{\prime \prime}(s) = E[x(x-1)s^{x-2}] = \lambda^2 exp[\lambda (s - 1)]
であることから、
G^{\prime \prime}(1) = E[x(x-1)] = \lambda^2
である。よって、分散$V[X]$は
V[X] = E[X(X-1)] + E[X] - (E[X])^2 = \lambda^2 + \lambda - \lambda^2 = \lambda
と求められる。
正規分布、ポアソン分布について
ここで例で登場した2つの確率密度関数、確率関数について簡単に紹介する。
正規分布
連続値の確率分布。
身長測定など、自然界や人間社会の中で多くの現象に当てはまる分布。
平均を中心に左右対称な分布である。
平均を$\mu$、分散を$\sigma^2$の正規分布は$N(\mu, \sigma^2)$と表され
その確率密度関数は以下の式で与えられる。
f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}exp[-\frac{(x - \mu)^2}{2\sigma^2}] \quad
(-\infty < x < \infty)
ここで
z = \frac{x - \mu}{\sigma}
とすると
dz = \frac{1}{\sigma}dx \Rightarrow \sigma dz = dx
より
f(z) = \frac{1}{\sqrt{2\pi}}exp(-\frac{z^2}{2}) \quad (-\infty < z < \infty)
となり、これは標準正規分布$N(0, 1^2)$の確率密度関数である。
イメージを掴んでいただけるように、以下にコードとヒストグラムを示す。
グラフの軸は以下いずれも横軸$x$、縦軸$f(x)$である。
# 分布をもとにデータを出力するために必要なライブラリ
import numpy as np
# 可視化ライブラリ
import matplotlib.pyplot as plt
# ランダムシードの設定
np.random.seed(0)
# Jupyter上でグラフをインライン表示する設定
%matplotlib inline
# 正規分布
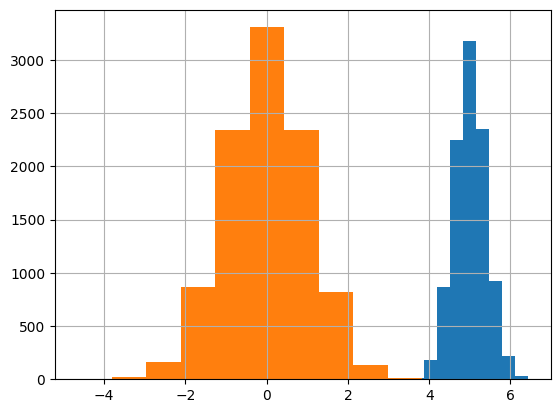
# np.random.normal(μ 、σ、サンプル数)
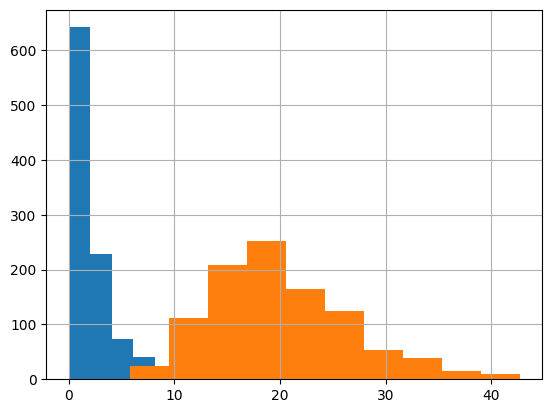
x = np.random.normal(5, 0.4, 10000)
plt.hist(x)
# 標準正規分布
y = np.random.normal(0, 1, 10000)
plt.hist(y)
plt.grid(True)
左が$N(0, 1^2)$, 右が$N(5, 0.4^2)$。
いずれも$\mu$を中心に左右対称な分布で、$\sigma$が大きくなると裾野が広がる様子がわかる。
二項分布
離散値の確率分布。
例では使われていないが次のポアソン分布を理解する上で必要になるので
ここで簡単に紹介する。
$n$回試行して確率$p$の事象が$x$回発生したとき、その確率関数は
f(x) = {}_nC_x p^x (1 - p)^{n - x}
となり、この確率分布を二項分布といい、$Bi(n, p)$で表す。($Bi$はBinominalの頭文字)
イメージを掴んでいただけるように、以下にコードとヒストグラムを示す。
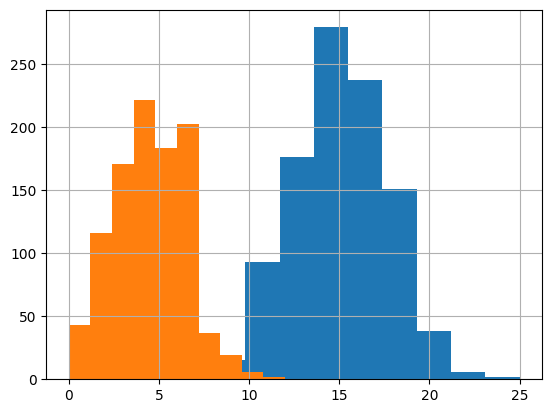
# 二項分布
# np.random.binominal(n, p, サンプル数)
x = np.random.binomial(30, 0.5, 1000)
plt.hist(x)
y = np.random.binomial(30, 0.15, 1000)
plt.hist(y)
plt.grid(True)
左が$Bi(30, 0.15)$, 右が$Bi(30, 0.5)$。
分布の山の位置に着目すると
$p$が小さい方が発生回数が小さい方に分布の山が寄る様子がわかる。
ポアソン分布
離散値の確率分布。
魚が釣れる数や営業で契約が取れる件数、自己破産件数など、非常に確率は低いが現実に起こっている事が観測される事象について当てはまる分布。
実は先程の二項分布の特殊な例として確率関数の式が導き出される。
前述の二項分布の確率関数において$np = \lambda$とすると
f(x) = {}_nC_x (\frac{\lambda}{n})^x (1 - \frac{\lambda}{n})^{n - x}
= \frac{n \cdot (n - 1) \cdots (n - x + 1)}{x!}(\frac{\lambda}{n})^x (1 - \frac{\lambda}{n})^{n} (1 - \frac{\lambda}{n})^{- x}
= \frac{1}{x!} \cdot 1 \cdot (1 - \frac{1}{n}) \cdots (1 - \frac{x - 1}{n}) \cdot \lambda^x \cdot (1 - \frac{\lambda}{n})^{n} \cdot (1 - \frac{\lambda}{n})^{- x}
ここで、試行回数$n$が非常に大きく、確率$p$が非常に小さい場合、すなわち
$n \rightarrow \infty , p \rightarrow 0$の極限を取ると
\lim_{n \to \infty} (1 - \frac{\lambda}{n})^n = e^{-\lambda}
であるから、
f(x) \to \frac{\lambda^x}{x!}e^{-\lambda}
となり、パラメータ$\lambda$のポアソン分布の確率関数が導かれ、$Po(\lambda)$で表す。
イメージを掴んでいただけるように、コードとヒストグラムを示す。
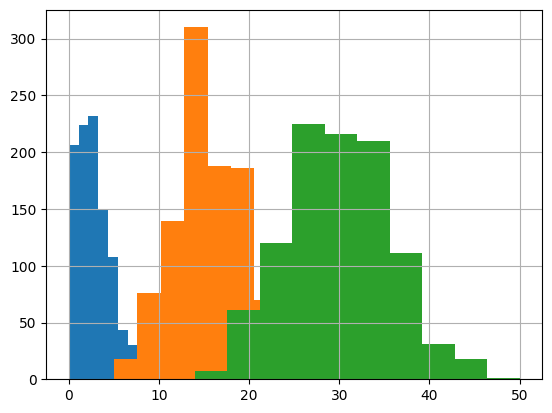
# ポアソン分布
# np.random.poisson(λ, サンプル数)
x = np.random.poisson(3, 1000)
plt.hist(x)
y = np.random.poisson(15, 1000)
plt.hist(y)
z = np.random.poisson(30, 1000)
plt.hist(z)
plt.grid(True)
左から順に、$Po(3), Po(15), Po(30)$である。
ここでは$\lambda$の値の変化に伴う分布形状の変化に着目すると、
$\lambda$の値が大きくなるにつれて、ポアソン分布→2項分布→正規分布と
分布が遷移している様子がわかる。
実際、二項分布において試行回数$n$を$n \to \infty$、事象の発生確率$p$を$p \to 0$とすると
ポアソン分布に近似でき、試行回数$n$を$n \to \infty$で正規分布に近似できる(二項分布の正規近似)事が知られている。
母関数について
母関数とは、確率分布を特徴づけ、確率分布に対して一意に対応する関数である。
ここでは確率母関数、モーメント母関数、特性関数を紹介する。
確率母関数
整数値をとる確率変数$X$が確率関数$f(X)$に従うとき、以下で与えられる関数
G(s) = E[s^x] = \sum_{x = 0}^{\infty} s^x f(x)
期待値$E[X]$や、階乗モーメント$E[X(X-1)\cdots1]$を算出するときに威力を発揮する
例:$G(s)$の$s$について導関数を求めると
\frac{d}{ds}G(s) = E[Xs^{x-1}]
\frac{d^2}{ds^2}G(s) = E[X(X-1)s^{X-2}]
\vdots
\frac{d^n}{ds^n}G(s) = E[X(X-1)\cdots(X-n+1)s^{X-n}]
ここで、$s=1$とすると
\frac{d}{ds}G(s) |_{s=1} = E[X]
\frac{d^2}{ds^2}G(s) |_{s=1} = E[X(X-1)]
\vdots
\frac{d^n}{ds^n}G(s) |_{s=1} = E[X(X-1)\cdots(X-n+1)]
となり、期待値及び階乗モーメントが求められる。
モーメント母関数
積率母関数とも呼ばれます。
連続値をとる確率変数$X$が確率密度関数$f(X)$に従うとき、以下で与えられる関数
M(\theta) = E[e^{x\theta}] = \int_{-\infty}^\infty e^{x\theta} f(x) dx
期待値$E[X]$や、$n$次モーメント$E[X^n] (n=1,2,\dots)$を算出するときに威力を発揮する
例:$M(\theta)$の$\theta$について導関数を求めると
\frac{d}{d\theta}M(\theta) = E[Xe^{\theta X}]
\frac{d^2}{d\theta^2}M(\theta) = E[X^{2}e^{\theta X}]
\vdots
\frac{d^n}{d\theta^n}M(\theta) = E[X^{n}e^{\theta X}]
ここで、$\theta=0$とすると
\frac{d}{d\theta}M(\theta) |_{\theta=0} = E[X]
\frac{d^2}{d\theta^2}M(\theta) |_{\theta=0} = E[X^{2}]
\vdots
\frac{d^n}{d\theta^n}M(\theta) |_{\theta=0} = E[X^{n}]
となり、期待値及び積率モーメントが求められる。
特性関数
前述2つの母関数は収束性の課題を抱えており、分布如何で関数が存在しない場合がある。
そこで、確率変数$X$が確率関数もしくは確率密度関数$f(X)$に従うとき、$i^2 = -1$を満たす虚数単位$i$に対して以下の式で与えられる関数
\varphi_X(t) = E[e^{itX}] = E[\cos(tX) + i\sin(tX)]
例えば、モーメント母関数を計算したものの広義積分が収束しない状況において
期待値$E[X]$や、$n$次モーメント$E[X^n] (n=1,2,\dots)$を算出するときに威力を発揮する
パラメータの最尤推定量を求める
最尤法を用いて、与えられたデータをもとに確率密度関数や確率関数のパラメータ($\sigma$、$\mu$など)の点推定値を求める問題です。
問題文としては、「〜の最尤推定量を求めよ」といった感じです。
最尤推定量を求める流れは次のとおりです。
- 尤度関数を求める
- 尤度関数の対数を取って対数尤度関数を求める
- 対数尤度関数を微分して、尤度方程式を導出する
- 尤度方程式を解き、最尤推定量を求める
ここでは、対数、偏微分の知識が必要となる。
また、尤度方程式を解析的に解けない場合、計算機で数値的に解く必要があり、
その場合はニュートン・ラプソン法等の数値解法のアルゴリズムに関する知識も必要になります。
以下に例を示します。
例1:尤度方程式が解析的に解けるケース
ここでは、対数正規分布のパラメータ$\mu$, $\sigma$がいずれも未定として、これらの最尤推定量を求める。
確率変数$X_1, X_2, \dots X_n$がそれぞれ独立に、対数正規分布$LN(\mu, \sigma^2)$に従うとし、
その確率密度関数は、$x > 0$として以下の式で与えられる
f(x) = \frac{1}{\sqrt{2\pi}\sigma}\frac{1}{x}exp[-\frac{(\ln x - \mu)^2}{2\sigma^2}]
確率変数$X_1, X_2, \dots X_n$の$LN(\mu, \sigma^2)$からの$n$個の独立な観測値を$x_1, x_2, \dots x_n$とすると
$\mu, \sigma^2$の尤度関数は次のように求められる
L(\mu, \sigma^2) = \prod_{i=1}^{n} f(x_i) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi}\sigma}\frac{1}{x_i}exp[-\frac{(\ln x_i - \mu)^2}{2\sigma^2}]
= \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}}\frac{1}{x_i}exp[-\frac{(\ln x_i - \mu)^2}{2\sigma^2}]
ここで、尤度関数の両辺で自然対数$\ln$を取ると、対数尤度関数は次のように求められる
l(\mu, \sigma^2) = \ln [ \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}}\frac{1}{x_i}exp[-\frac{(\ln x_i - \mu)^2}{2\sigma^2}]]
= \ln [(\frac{1}{\sqrt{2\pi\sigma^2}})^n \prod_{i=1}^{n}[\frac{1}{x_i} exp[-\frac{(\ln x_i - \mu)^2}{2\sigma^2}]]]
= -\frac{n}{2} \ln(2\pi\sigma^2) - \ln \prod_{i=1}^{n}x_i + \ln [\prod_{i=1}^{n}exp[-\frac{(\ln x_i - \mu)^2}{2\sigma^2}]]
= -\frac{n}{2} \ln(2\pi\sigma^2) - \sum_{i=1}^{n}\ln x_i - \sum_{i=1}^{n}\frac{(\ln x_i - \mu)^2}{2\sigma^2}
対数尤度関数を$\mu, \sigma^2$についてそれぞれ偏微分することにより、それぞれのパラメータに対する
尤度方程式は以下のように導出される。
\frac{\partial}{\partial \mu} l(\mu, \sigma^2) = \sum_{i=1}^{n}\frac{(\ln x_i - \mu)}{\sigma^2} = 0
\frac{\partial}{\partial \sigma^2} l(\mu, \sigma^2) = -\frac{n}{2\sigma^2} + \frac{1}{2(\sigma^2)^{2}} \sum_{i=1}^{n}(\ln x_i - \mu)^2 = 0
前述の2式を$\mu, \sigma^2$についての連立方程式として解く。第1式より
\sum_{i=1}^{n}\frac{(\ln x_i - \mu)}{\sigma^2} = 0 \Rightarrow \sum_{i=1}^{n}\ln x_i - n\mu = 0
より、$\mu$の最尤推定量$\hat{\mu}$は
\hat{\mu} = \frac{1}{n} \sum_{i=1}^{n}\ln x_i
と求められる。
ここで、
\hat{\mu} = \bar{x} = \frac{1}{n}\sum_{i=1}^{n}\ln x_i
として連立方程式の第2式を$\sigma^2$について解くと、$\sigma^2$の最尤推定量$\hat{\sigma^2}$は
\hat{\sigma^2} = \frac{1}{n}\sum_{i=1}^{n}(\ln x_i - \hat{\mu})^2 = \frac{1}{n}\sum_{i=1}^{n}(\ln x_i - \bar{x})^2
と求められる。
対数正規分布について
正の連続値の確率分布。
世帯の所得の分布などに当てはまる分布。
名前から分かる通り、その確率密度関数は以下のように正規分布から導き出せる。
確率変数$X$が正規分布$N(\mu, \sigma^2)$に従っているとき
確率変数$Y = e^X$の確率分布を求める。
$Y=e^X$の両辺で対数を取ると$\ln Y = X$、両辺を$X$で微分すると
\frac{d}{dX} \ln Y = \frac{d}{dX} X \Rightarrow \frac{dY}{dX}(\frac{d}{dY} \ln Y) = \frac{d}{dX} X \Rightarrow \frac{dY}{dX} (\frac{1}{Y}) = 1
\Rightarrow \frac{dX}{dY} = \frac{1}{Y}
となる。ここで、正規分布$N(\mu, \sigma^2)$の確率密度関数
f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}exp[-\frac{(x - \mu)^2}{2\sigma^2}] \quad (-\infty < x <\infty)
を確率変数$Y$の関数として変形する。
まず、$f(y)\cdot dy$と$f(x)\cdot dx$はそれぞれ確率密度関数の積分値で
互いに等しくなることから
f(y)dy = f(x)dx \Rightarrow f(y) = \frac{dx}{dy}f(x)
したがって、
f(y) = \frac{1}{\sqrt{2\pi\sigma^2}} \frac{1}{y}exp[-\frac{(\ln y - \mu)^2}{2\sigma^2}] \quad (y > 0)
となり、これが対数正規分布の確率密度関数であり、$NL(\mu, \sigma^2)$で表す。
なお、$y>0$は対数の真数条件からも明らかである。
イメージを掴んでいただけるように、以下にコードとヒストグラムを示す。
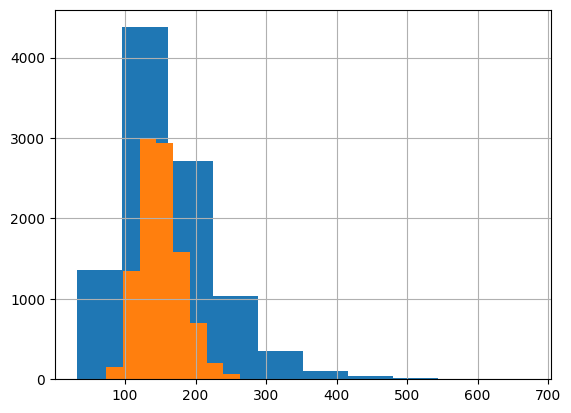
# 対数正規分布
# np.random.lognormal(μ 、σ、サンプル数)
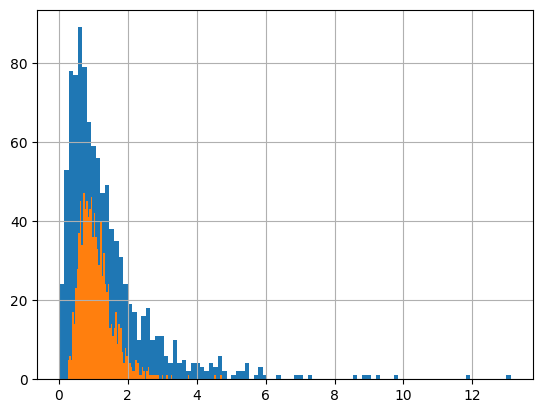
x = np.random.lognormal(5,0.4,10000)
plt.hist(x)
y = np.random.lognormal(5,0.2,10000)
plt.hist(y)
plt.grid(True)
青色が$NL(5, 0.4^2)$、オレンジ色が$NL(5, 0.2^2)$である。
$\sigma$が小さくなるにつれて山が小さくなっている様子がわかる。
正規分布の場合と異なり、裾野の広がりが小さくなるだけでなく
山の高さまで低くなっているところが興味深い。
最尤法について
現実のデータ分析において、確率密度関数や確率関数が予めわかってるケースは
非常に稀で、実際には実測値をもとに求める必要がある。
そのようなケースにおいて有用な手法が最尤法だ。
ざっくり説明すると
実測値をもとに、最も尤もらしい確率分布のパラメータを点推定する方法
である。
これだけだとわかりにくいので、前述の例1を用いて少し詳細を説明する。
確率変数$X_1, X_2, \dots X_n$の$LN(\mu, \sigma^2)$からの$n$個の独立な観測値を$x_1, x_2, \dots x_n$とすると、$\mu, \sigma^2$の尤度関数は次のように求められる
L(\mu, \sigma^2) = \prod_{i=1}^{n} f(x_i) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi}\sigma}\frac{1}{x_i}exp[-\frac{(\ln x_i - \mu)^2}{2\sigma^2}]
ここで求めた尤度関数の式の形に着目すると、確率の積となっていることから、
尤度とは同時確率であり、最尤法とは同時確率を最大にするパラメータを求める方法
と理解できる。
ここから先は尤度関数の最大値を与えるパラメータを求めるのだが、
このままでは後の微分計算が非常につらいので、
以下のように両辺の対数をとって対数尤度関数を求める。
l(\mu, \sigma^2) = \ln [ \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}}\frac{1}{x_i}exp[-\frac{(\ln x_i - \mu)^2}{2\sigma^2}]]
= \ln [(\frac{1}{\sqrt{2\pi\sigma^2}})^n \prod_{i=1}^{n}[\frac{1}{x_i} exp[-\frac{(\ln x_i - \mu)^2}{2\sigma^2}]]]
= -\frac{n}{2} \ln(2\pi\sigma^2) - \ln \prod_{i=1}^{n}x_i + \ln [\prod_{i=1}^{n}exp[-\frac{(\ln x_i - \mu)^2}{2\sigma^2}]]
= -\frac{n}{2} \ln(2\pi\sigma^2) - \sum_{i=1}^{n}\ln x_i - \sum_{i=1}^{n}\frac{(\ln x_i - \mu)^2}{2\sigma^2}
後は対数尤度関数に対する最大値問題と考えることができ、最大=極大と考えて
推定パラメータそれぞれに対する偏微分=0となる点を求める方程式(尤度方程式)
をもとめると、
\left\{
\begin{array}{ll}
\frac{\partial}{\partial \mu} l(\mu, \sigma^2) = \sum_{i=1}^{n}\frac{(\ln x_i - \mu)}{\sigma^2} = 0 \\
\frac{\partial}{\partial \sigma^2} l(\mu, \sigma^2) = -\frac{n}{2\sigma^2} + \frac{1}{2(\sigma^2)^{2}} \sum_{i=1}^{n}(\ln x_i - \mu)^2 = 0
\end{array}
\right.
この例では、推定パラメータが2つなので、2式を連立して解くことになる。
対数尤度関数の導出について
尤度関数から対数尤度関数の導出途中の計算が若干わかりにくいかもなので
よりシンプルな式を例に補足します。
実数列$a_i (i=1,2, \dots N)$の$N$個の積
\prod_{i=1}^{N} a_i = a_1 \cdot a_2 \cdots a_N
において、両辺の対数を取ると
\log \prod_{i=1}^{N} a_i = \log (a_1 \cdot a_2 \cdots a_N)
ここで右辺は、対数公式$\log(ab) = \log a + \log b$より
\log (a_1 \cdot a_2 \cdots a_N) = \log a_1 + \log a_2 + \cdots + \log a_N
であるから
\log \prod_{i=1}^{N} a_i = \sum_{i=1}^{N} \log a_i
となる。
例2:尤度方程式が解析的に解けないケース
大変悲しいことだが、現実世界では尤度方程式が解析的に解けない場合がある。
その場合、面倒だがプログラムを書いて計算機を用いて数値解を求めることになる。
ここでは、アルゴリズムが比較的平易なニュートン・ラプソン法による解法を紹介する。
確率変数$X_1, X_2, \dots X_n$がそれぞれ独立に確率密度関数$f(x|\theta)$に従うとして
未知のパラメータ$\theta$の最尤推定量を求める事を考える。ここで、$\textbf{x} = (x_1,\dots,x_n)$であり
簡単のため$\theta$は一次元とする。
このとき、尤度関数は
L(\theta, \textbf{x}) = f_n(\textbf{x}|\theta) = \prod_{i=1}^{n}f(x_i|\theta)
である。この式において両辺対数を取ると対数尤度関数は次のように求められる。
l(\theta, \textbf{x}) = \ln f_n(\textbf{x}|\theta) = \sum_{i=1}^{n}\ln f(x_i|\theta)
ここで、$\theta$の最尤推定量$\hat{\theta}$は以下の尤度方程式の解として与えられる。
l^{\prime}(\theta, \textbf{x}) = \frac{d}{d\theta} l(\theta, \textbf{x}) = 0
次に、この尤度方程式を数値的に解く、すなわち、方程式の近似解を求めるために、
$l^{\prime}(\hat{\theta}, \textbf{x})$を$\hat{\theta} = \theta$近傍でテーラー展開すると
0 = l^{\prime}(\hat{\theta}, \textbf{x}) = l^{\prime}(\theta, \textbf{x}) + l^{\prime \prime}(\theta, \textbf{x})(\hat{\theta} - \theta) + \textbf{O}_p(1)
となり、$l^{\prime}(\hat{\theta}, \textbf{x}) = 0$より、
\hat{\theta} = \theta + \frac{l^{\prime}(\theta, \textbf{x})}{-l^{\prime \prime}(\theta, \textbf{x})} + \textbf{O}_p(n^{-1})
ここで、$\theta, \hat{\theta}$をそれぞれ$\theta_{k-1}, \theta_{k}$と置くことにより、次のようなアルゴリズムを構成できる。
Step 0. 初期値$\theta_0$と解の精度$\varepsilon (> 0)$の値を決める
Step 1. $k$回目の反復によって$\theta_{k}$が得られたとし、$\theta_{k+1}$を次式で定める。
\theta_{k+1} = \theta_{k} + \frac{l^{\prime}(\theta_{k}, \textbf{x})}{-l^{\prime \prime}(\theta_{k}, \textbf{x})}
Step 2. $k$を$k + 1$にインクリメントして反復する。
Step 3. 収束条件$|\theta_{k+1} - \theta_{k}| < \varepsilon$ を満たすとき終了し、$\theta_{k+1}$を解とする。
実装は統計検定の範囲外ですが、せっかくなのでPythonのコード例を示す。
例:尤度方程式$e^{x^2} - 4x +1 = 0$の数値解を求める。(尤度方程式はめっちゃ適当)
import numpy as np
def f(x):
return np.exp(x**2)-4*x+1
def df(x):
return 2*x*np.exp(x**2)-4
# 初期値(適当に割り当てるが、ここの値如何では答えが出ない場合がある)
x=3
# 要求精度
epsilon = 0.00001
print("n\t x\t f(x)")
n = 1
while True:
x = x - f(x)/df(x)
print("{}\t{:.5f}\t{:.5f}".format(n, x, f(x)))
n += 1
if abs(f(x)) < epsilon:
break
print("x = %f" % x)
実行すると次のようになります。反復ごとに解に近づいていく様子がわかります。
n x f(x)
1 2.83355 3058.28300
2 2.65764 1158.38650
3 2.47094 439.44539
4 2.27224 166.60794
5 2.06131 62.79104
6 1.84079 23.25834
7 1.61939 8.29163
8 1.41514 2.74795
9 1.25320 0.79628
10 1.15432 0.17307
11 1.11789 0.01767
12 1.11324 0.00026
13 1.11317 0.00000
x = 1.113173
結果は$x = 1.113173$という値になります。
ついでにScipyを使った実装例を紹介する。
import numpy as np
from scipy.optimize import newton
def f(x):
return np.exp(x**2) - 4*x + 1
x = 3
epsilon = 0.00001
print("x = ", newton(f, x, tol = epsilon))
Scipyを使うとこのように簡単に実装出来るが、アルゴリズムの理解のために敢えて最初にスクラッチによる実装を最初に紹介した。
ニュートン・ラプソン法は対数尤度関数の導関数並びに2階導関数が比較的求めやすい状況下では有効な手段だが、不完全なデータを扱う場合は尤度方程式が複雑な形になり厳しいケースがある。こうした状況では、EMアルゴリズムの採用を検討する。
なお、EMアルゴリズムの詳細については今回の範疇を大きく超えるので
興味のある方は現代数理統計学の基礎の第11章:計算統計学の方法をご覧いただきたい。
ただ、統計検定1級の過去問を見るとちょいちょい出題されているので
気が向いたら別の記事で扱うかもしれない。
確率密度関数の変数変換
すでにお気づきかもしれないが、実は正規分布の確率密度関数から対数正規分布のそれを導き出す過程が本セクションで紹介する確率密度変数の変数変換である。
ここではもう少し複雑な例を紹介する。必要となる知識は微分、積分、行列式である。
例1:確率変数の平方(2乗)の確率分布
確率変数$Z$が標準正規分布$N(0, 1^2)$に従っているとき、$V=Z^2$の確率分布を求める。
まず、両辺を$Z$で微分する。$Z > 0$のとき、$Z = \sqrt{V}$であるから、
\frac{dV}{dZ} = 2Z \Rightarrow \frac{dZ}{dV} = \frac{1}{2\sqrt{V}}
$Z$の分布は標準正規分布なので、原点について左右対称であることから、
f(v)dv = 2 \cdot f(z)dz \Rightarrow f(v) = 2f(z)\frac{dz}{dv}
よって、求める確率密度関数は、
f(v) = 2 \cdot \frac{1}{\sqrt{2\pi}}exp(-\frac{z^2}{2}) \cdot \frac{1}{2\sqrt{v}}
= \frac{1}{\sqrt{2\pi}}\frac{1}{\sqrt{v}}exp(-\frac{v}{2}) \quad (v > 0)
となる。ちなみにこれは、自由度1の$\chi^{2}$(カイ2乗)分布であり、$\chi^2(1)$と表される。
例2:2つの確率変数の比の確率分布
2つの確率変数$X, Y$が互いに独立に自由度1の$\chi^{2}$分布に従うとき、
確率変数$S = \frac{X}{Y}$の確率分布を求める。
まず、$X=x$,$Y=y$の事象が同時に発生する確率を考える。
すなわち、$X, Y$についての同時確率密度関数を求めると、$X, Y$は互いに独立であることから
f(x, y) = \frac{1}{\sqrt{2\pi}}\frac{1}{\sqrt{x}}exp(-\frac{x}{2}) \cdot \frac{1}{\sqrt{2\pi}}\frac{1}{\sqrt{y}}exp(-\frac{y}{2})
= \frac{1}{2\pi}\frac{1}{\sqrt{xy}}exp(-\frac{x + y}{2})
ここで変数変換
\left\{
\begin{array}{ll}
s = \frac{x}{y} \\
u = y
\end{array}
\right.
とすると、$x = su, y = u$より変換のヤコビアン(ヤコビ行列式)は、
\frac{\partial(x, y)}{\partial(s, u)} =
\begin{vmatrix}
\frac{\partial x}{\partial s} & \frac{\partial x}{\partial u} \\
\frac{\partial y}{\partial s} & \frac{\partial y}{\partial u}
\end{vmatrix}
= \frac{\partial x}{\partial s}\cdot \frac{\partial y}{\partial u} - \frac{\partial x}{\partial u} \cdot \frac{\partial y}{\partial s} = u \cdot 1 - s \cdot 0 = u
と求められる。よって、変換後の変数$S, U$の確率密度関数は、
g(s, u) = f(x, y) \cdot \frac{\partial(x, y)}{\partial(s, u)}
= \frac{1}{2\pi}\frac{1}{\sqrt{xy}}exp(-\frac{x + y}{2}) \cdot u
$x + y = u(s + 1), xy = su^2$より
g(s, u) = \frac{1}{2\pi}\frac{1}{\sqrt{su^2}}exp(-\frac{u(s+1)}{2})u
= \frac{1}{2\pi}\frac{1}{\sqrt{s}}exp(-\frac{u(s+1)}{2})
よって、確率変数$S$の確率密度関数は、$u > 0$におけるそれぞれの$u$の値に対する確率を
足し合わせる、すなわち、$g(s, u)$を$u>0$の範囲で$u$について積分すると
次のように求められる。
g(s) = \int_0^\infty \frac{1}{2\pi}\frac{1}{\sqrt{s}}exp(-\frac{u(s+1)}{2})du
= \frac{1}{2\pi}\frac{1}{\sqrt{s}}\int_0^\infty exp(-\frac{u(s+1)}{2})du
= \frac{1}{2\pi}\frac{1}{\sqrt{s}}[-\frac{2}{s+1}exp(-\frac{u(s+1)}{2})]_0^\infty
= \frac{1}{\pi\sqrt{s}}\frac{1}{1 + s}
となる。ちなみにこれは、自由度$(1,1)$の$F$分布であり、$F(1,1)$と表される。
カイ2乗分布、F分布について
ここで例で登場した2つの確率分布について簡単に紹介する。
カイ2乗分布
$m$個の確率変数$Z_1, Z_2, \dots Z_m$がそれぞれ独立に標準正規分布$N(0,1)$に従うとする。
このとき、確率変数の二乗和
W = \sum_{i=1}^{m} Z_i^2
が従う確率分布を、自由度$m$の$\chi^2$(カイ2乗)分布といい、$\chi^2(m)$で表す。
標本の二乗和に関する分布なので、標本分布の一種である。
なお、確率密度関数の式については複雑なのでここでは省略する。
イメージを掴んでいただけるように、以下にコードとヒストグラムを示す。
# カイ二乗分布
# np.random.chisquare(自由度,サンプル数)
x = np.random.chisquare(2,1000)
plt.hist(x)
y = np.random.chisquare(20,1000)
plt.hist(y)
plt.grid(True)
自由度(ここではざっくりと標本数)の増加とともに分布がなだらかになる
様子がわかる。
F分布
2つの確率変数$W_1, W_2$がそれぞれ独立に自由度$m_1, m_2$の$\chi^2$分布に従うとする。
このとき
F = \frac{\frac{W_1}{m_1}}{\frac{W_2}{m_2}}
が従う確率分布を、自由度$(m_1, m_2)$の$F$分布といい、$F(m_1, m_2)$で表す。
標本の二乗和の比に関する分布なので、こちらも標本分布の一種である。
なお、こちらも確率密度関数の式については複雑なのでここでは省略する。
イメージを掴んでいただけるように、以下にコードとヒストグラムを示す。
# F分布
# np.random.f(自由度1,自由度2,サンプル数)
x = np.random.f(6,7,1000)
plt.hist(x, 100)
y = np.random.f(20,25,1000)
plt.hist(y, 100)
plt.grid(True)
自由度(ここではざっくりと標本数)の増加とともに分布がなだらかになる
様子がわかる。
振り返り
この記事を書いている時点ではまだ結果がわかっていないが、
おそらく不合格である体で書く。
今年の反省点は、勉強が途中で息切れしたこと。
その原因を次のように考えている。
- 適切なマイルストーンが設定出来ていなかったこと
- 勉強開始時期があまりに早すぎた
今度は、1級という大きな山を登る前に、
ちょっと大きな山として準1級を間に挟んで再び挑戦したいと思う。
また、本番での答案作成速度も全く足りていなかった事も反省点だ。
この点については、少なくとも本番1ヶ月前からは本番の試験時間を想定した
答案作成練習を実施する事で改善したい。
また、日々の仕事を通じて文章作成力が磨かれ、その結果が
統計検定1級本番での答案作成能力に必ずや活きるだろうと信じている。
そして、来年の今頃は
「統計検定1級受験戦記 完結編 〜正規分布よ永遠なれ〜」
のタイトルで合格報告を書いているであろうことを目指し、
関東の桜の季節くらいからぼちぼち勉強再開する予定。
さいごに
スタンバイでは一緒に求人エンジンスタンバイの開発をしてく仲間を募集中です!
カジュアル面談で弊社の事業や技術等について説明させていただければと思うので
興味を持たれた方はぜひご連絡ください!
笑撃の退職エントリーから始まったスタンバイ Advent Calendar 2023もいよいよ明日を残すのみとなりました。大トリを飾るのは我らがCOO、@satoshi-yamamotoさんです。
乞うご期待!!
ではでは、良いクリスマス![]() と新年
と新年![]() を〜。
を〜。
追伸
続編制作決定!! (統計数理、統計応用ともに不合格)
2024冬公開に向けて2024春から制作開始。