ELMoとBERTを使って多義語に対して単語の類似度判定をする

概要

文脈を考慮した単語分散表現（埋め込みベクトル）を計算するエンコーダーモデルであるELMoが複数の意味を持つ多義語を区別できるかどうか、単語の類似度を計算することで検証します。多義語とは例えば次のようなものです。

• What do you mean? （どういう意味？）
• a mean person （ケチな人）
• the mean value （平均値）

同じ検証を近年の自然言語処理モデルのデファクトスタンダードであるBERTに対しても行い、結果を比較します。

（2020/4/8追記）
埋め込みベクトルを取り出す層によって結果がどう変わるかを追加検証しました。

環境・使用モデル

計算はすべてGoogle Colaboratory上で行いました。

モデルはELMo, BERTともに英語の学習済みモデルをファインチューニングなしでそのまま使います。ELMoはTensorFlow Hub、BERTは公式リポジトリのものを使用します。

問題設定

Word2vecやGloVeといったモデルでは一つの単語に対して一つの埋め込みベクトルが得られるため、多義語がどういった意味で使われているのかを区別することはできません。一方、ELMoやBERTといったモデルでは、同じ単語であっても文脈によって異なる埋め込みベクトルが得られるため、多義語を使われている意味によって区別することが可能だと期待できます。

今回は、「右」「正しい」「権利」という意味を持つ"right"を例にとり、以下の例文を使います。

• 「右」という意味
  My right arm is broken.
Cover your right eye.
Please turn right at the next corner.
I got into the right lane.

• 「正しい」という意味
  Your opinion is more or less right.
I got the answer right.
Please try to make things right again.
It was quite right of you to refuse the offer.

• 「権利」という意味
  I don't have a right to access that computer.
Everyone has a right to enjoy his liberty.
She has the right to criticize the government.
Every person has a right to defend themselves.

これらの例文を学習済みモデルに入力して"right"に対応する埋め込みベクトルを取り出し、コサイン類似度

cossim(\mathbf{u} ,\mathbf{v} ) = \frac{\mathbf{u} \cdot \mathbf{v}}{|\mathbf{u}| \, |\mathbf{v}|}

を計算することで、同じ意味の"right"どうしの類似度が高くなるかを調べます。

実装

必要なライブラリをインポートします。TensorFlowのバージョンはELMo、BERTともに1.x系を使用しますが、2020年3月27日以降、Google Colaboratoryのデフォルトは2.x系になっていますので、マジックコマンド%tensorflow_version 1.xで1.x系を指定しています。

import json
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

%tensorflow_version 1.x
import tensorflow as tf
import tensorflow_hub as hub

検証に使う文章を用意します。BERTでは入力データをファイルから読み込ませる必要があるのでテキストファイルにも書き込んでおきます。

right_texts = ["My right arm is broken",
               "Cover your right eye",
               "Please turn right at the next corner",
               "I got into the right lane",
               "Your opinion is more or less right",
               "I got the answer right",
               "Please try to make things right again",
               "It was quite right of you to refuse the offer",
               "I don't have a right to access that computer",
               "Everyone has a right to enjoy his liberty",
               "She has the right to criticize the government",
               "Every person has a right to defend themselves",]

with open('right_texts.txt', mode='w') as f:
    f.write('\n'.join(right_texts))

コサイン類似度の相関行列を計算する関数を用意しておきます。

def cos_sim(v1, v2):
  return np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))
  
def calc_sim_mat(arr):
  num = len(arr) # number of vectors contained in arr
  sim_mat = np.zeros((num, num))
  norm = np.apply_along_axis(lambda x: np.linalg.norm(x), 1, arr) # norm of each vector
  normed_arr = arr / np.reshape(norm, (-1,1))
  for i, vec in enumerate(normed_arr):
    sim = np.dot(normed_arr, np.reshape(vec, (-1,1)))
    sim = np.reshape(sim, -1) # flatten
    sim_mat[i] = sim
  return sim_mat

ELMo

ELMoはTensorFlow Hubの学習済みモデル(v3)を使用します。使い方は本家ページに書いてありますが、

文脈を考慮したWord Embedding, ELMoをTensorFlow Hubを使って試してみる

も参考にしました。（実は今回の記事を書こうと思ったのは上記の記事を読んだのがきっかけです。）

ELMoモジュールは、スペースで区切られた文章を入力するモードsignature="default"と単語ごとに分割したトークンのリストを入力するモードsignature="tokens"がありますが、今回は後者を使います。そのため、tokenizerという関数を用意して、文章をトークン化・パディングしています。

elmo_url = "https://tfhub.dev/google/elmo/3"

def tokenizer(texts):
  PAD = ""
  tokens = [s.lower().split() for s in texts]
  lengths = [len(t) for t in tokens]
  max_len = max(lengths)
  tokens = [t + [PAD] * (max_len - len(t)) for t in tokens]
  return tokens, lengths

def elmo_embed(texts):
    tokens, lengths = tokenizer(texts)
    elmo = hub.Module(elmo_url, trainable=False)
    embeddings = elmo(
        inputs={
        "tokens": tokens,
        "sequence_len": lengths
        },
        signature="tokens",
        as_dict=True)

    with tf.Session() as sess:
        sess.run(tf.global_variables_initializer())
        sess.run(tf.tables_initializer())
        embeddings_dict = sess.run(embeddings)

    return tokens, embeddings_dict

計算を実行して埋め込みベクトルを出力します。

tokens, elmo_embeddings_dict = elmo_embed(right_texts)
print(elmo_embeddings_dict.keys())
# dict_keys(['lstm_outputs1', 'lstm_outputs2', 'word_emb', 'sequence_len', 'elmo', 'default'])

TensorFlow Hubのページで説明してある通り、ELMoモジュールの出力は各種の埋め込みベクトルを収納した辞書です。各keyの説明は以下の通りです。

• word_emb: the character-based word representations with shape [batch_size, max_length, 512].
• lstm_outputs1: the first LSTM hidden state with shape [batch_size, max_length, 1024].
• lstm_outputs2: the second LSTM hidden state with shape [batch_size, max_length, 1024].
• elmo: the weighted sum of the 3 layers, where the weights are trainable. This tensor has shape [batch_size, max_length, 1024]
• default: a fixed mean-pooling of all contextualized word representations with shape [batch_size, 1024].

word_embは1層目の文脈を考慮しない埋め込み層の出力です。このベクトルだけ次元が512ですが、他のベクトルと和を取るときには、word_embベクトルを2つ結合して次元を1024にしているようです。
原論文にある通り、ELMoの出力はword_emb、lstm_outputs1、lstm_outputs2の３つの埋め込みベクトルを訓練可能な係数で線形和を取ったもので、それがelmoに収められています。今回は下流タスクの訓練はしないので、モジュールを呼ぶときにtrainable=Falseを指定したのですが、その場合ELMoベクトルの係数がどうなるのかについてはTensorFlow Hubでは言及されていません。今回の計算で得られたベクトルの値を調べたところ、どうやら係数は単純に1/3ずつになっているようです。また、trainable=Trueを指定してもELMoベクトルの値は変わりませんでしたので、訓練可能な重みの初期値もすべて1/3のようです。
defaultは文章内のすべての単語のELMoベクトルの平均をとったものです。文章全体の分散表現と解釈できるものだと思います。
sequence_lenは上の説明には含まれていませんが、各文章のトークン数（パディングは除く）を収めたリストです。

原論文によると、LSTMの1層目の出力は構文的(syntactic)な情報を、2層目は意味的(semantic)な情報を捉える傾向があるそうなので、単語の意味を分類するという今回のタスクの内容を鑑みて、まずはlstm_outputs2を使うこととします。
以下の関数で"right"の埋め込みベクトルのみを取り出します。

def my_index(l, x, default=-1):
  return l.index(x) if x in l else default

def find_position(tokens, word):
  pos = [my_index(t, word) for t in tokens]
  assert -1 not in pos
  return pos

def extract_elmo_vectors(embeddings_dict, tokens, word, layer):
  embeddings = embeddings_dict[layer]
  num_sentences = embeddings.shape[0]
  vec_dim = embeddings.shape[2]
  vectors = np.zeros((num_sentences, vec_dim))
  pos = find_position(tokens, word)
  for i in range(num_sentences):
    vectors[i] = embeddings[i][pos[i]][:]
  return vectors

elmo_vectors = extract_elmo_vectors(elmo_embeddings_dict, tokens, 'right', 'lstm_outputs2')
print(elmo_vectors.shape)
# (12, 1024)
elmo_sim_mat = calc_sim_mat(elmo_vectors)

これで、各文章の"right"に対する埋め込みベクトルelmo_vectorsと類似度の相関行列elmo_sim_matが得られました。結果を見る前にBERTでも同じ計算をします。

BERT

BERTは下流タスクに対して教師あり学習によりファインチューニングして使うことを念頭に置いたモデルですが、bert-as-serviceのように文章の分散表現を得るためのエンコーダーとして使うこともできます。今回はBERTを使って単語の分散表現を計算します。

まず、BERTの公式リポジトリをクローンします。

!git clone https://github.com/google-research/bert.git

モデルはBERT-Base, Uncasedを使うことにします。学習済みのパラメータをダウンロードして展開します。

!wget https://storage.googleapis.com/bert_models/2018_10_18/uncased_L-12_H-768_A-12.zip && \
unzip uncased_L-12_H-768_A-12.zip && \
rm uncased_L-12_H-768_A-12.zip

埋め込みベクトルを取り出すためのコードは公式リポジトリにextract_features.pyが用意されていますので、以下のように実行するだけです。--input_fileで用意したインプットファイルを指定、--output_fileは出力を保存する任意の名前のjsonlファイルを指定します。続く3つの引数は上でダウンロードした学習済みモデルを指定しています。--layersは埋め込みベクトルとして使う出力層を指定するもので、後ほど行う検証のためにすべての層を指定しておきます。

!python ./bert/extract_features.py \
  --input_file=right_texts.txt \
  --output_file=right_output.jsonl \
  --vocab_file=uncased_L-12_H-768_A-12/vocab.txt \
  --bert_config_file=uncased_L-12_H-768_A-12/bert_config.json \
  --init_checkpoint=uncased_L-12_H-768_A-12/bert_model.ckpt \
  --do_lower=True \
  --layers 0,1,2,3,4,5,6,7,8,9,10,11

出力されたjsonlファイルから目的の単語トークンに対応した埋め込みベクトルを取り出す関数を用意します。こちらのページを参考にしました。

def extract_bert_vectors(input_path, target_layer=-2, target_token): 
  with open(input_path, 'r') as f:
      output_jsons = f.readlines()
  
  vectors = []
  for output_json in output_jsons:
      output = json.loads(output_json)
      for feature in output['features']:
          if feature['token'] != target_token: continue
          for layer in feature['layers']:
              if layer['index'] != target_layer: continue
              vectors.append(layer['values'])
  return np.array(vectors)

"right"に対応するベクトルを取り出して、類似度の行列を計算します。ベクトルを取り出す層は最後から２番目とします。

bert_vectors = extract_bert_vectors('./right_output.jsonl', target_layer=10, target_token='right')
print(bert_vectors.shape)
# (12, 768)
bert_sim_mat = calc_sim_mat(bert_vectors)

結果

それでは、計算結果をプロットしてみます。seabornのheatmapを使ったプロット用の関数を定義します。

def show_sim_mat(sim_mat, texts, title=None, export_fig=False):
  sns.set(font_scale=1)
  g = sns.heatmap(
      sim_mat,
      vmin=0,
      vmax=1,
      cmap="YlOrRd")
  g.set_xticklabels(texts, rotation='vertical')
  g.set_yticklabels(texts, rotation=False)
  if title:
    plt.title(title, fontsize=24)
  if export_fig:
    plt.savefig(export_fig, bbox_inches='tight')
  plt.show()

ELMoとBERTの結果に対して実行します。

show_sim_mat(elmo_sim_mat, right_texts, title='ELMo')
show_sim_mat(bert_sim_mat, right_texts, title='BERT')

結果は以下の通りになりました。"right"に対応したベクトルの類似度をプロットしていますが、ラベルには文章全体を表示しています。同じ意味で"right"が使われている文章を4つずつ並べましたので、4つずつの対角ブロックの色が濃く、それ以外の非対角部分の色が薄くなるのが理想なのですが、いかがでしょうか。

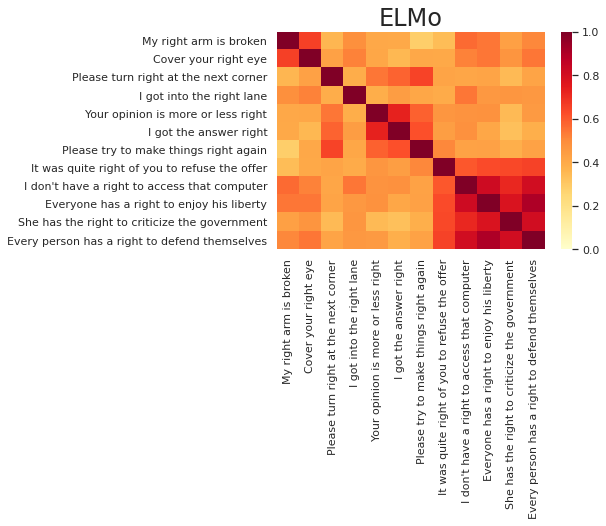
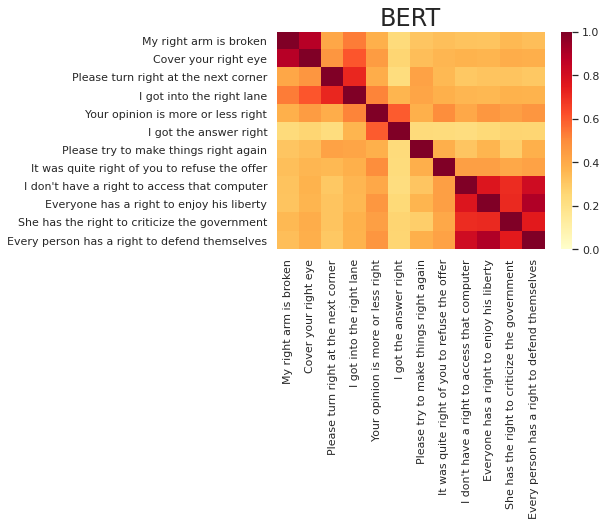
まず、どちらの図でも、「権利」の意味の最後のブロックの類似度が明らかに高くなっているのが見て取れます。この"right"はどれも"have/has"や"to"とセットで使われており、文の構造も似通っているので、他の意味と区別しやすいというのは納得のいく結果ではないでしょうか。「右」と「正しい」に関しては、「権利」ほどはっきりとは区別できていませんが、最初の2文のように同じ意味どうしの類似度が確かに高くなっているところも見受けられます。

ELMoとBERTの比較に関しては、目で見る限りはBERTのほうが良さそうです。しかし、コサイン類似度はモデルによって全体的な値の水準が異なる傾向があるため、類似度の値そのものよりも類似度の順序を見ることが重要です。そこで、類似度の順序に基づいた定量的な指標を導入して、両モデルを比較します。

以下の関数で、モデルの予測に対する適合率(precision)を計算します。block_sizeは単語が同じ意味で使われている文章の数のことで、今の例だと4です。各文章ごとに類似度が高い順に並べて、順位がblock_size位以内の文章が、同じ意味で多義語が使われているとモデルが予測した文章となります。ただし、順位1位は常に自分自身なので除きます。各文章ごとのblock_size-1個の予測に対する適合率をリストpoints_arrに収納し、それらの平均をav_pointで与えています。

def eval_precision(sim_mat, block_size):
  num_data = len(sim_mat)
  precision_list = []
  for i in range(num_data):
    block_id = int(i / block_size)
    pred = np.array([1 if (block_id * block_size <= j and j < (block_id+1) * block_size) 
                    else 0 for j in range(num_data)])
    sorted_args = np.argsort(sim_mat[i])[::-1]
    sorted_pred = pred[sorted_args]
    precision = np.mean(sorted_pred[1:block_size])
    precision_list.append(precision)
  precision_arr = np.array(precision_list)
  av_precision = np.mean(precision_arr)
  return av_precision, precision_arr

実行した結果は以下の通りです。

# ELMo
elmo_av_precision, elmo_precision_arr = eval_precision(elmo_sim_mat, 4)
print(np.round(elmo_av_precision, 2))
# 0.61
print(np.round(elmo_precision_arr, 2))
# [0.33 0.33 0.   0.67 0.67 0.67 0.67 0.   1.   1.   1.   1.  ]

# BERT
bert_av_precision, bert_precision_arr = eval_precision(bert_sim_mat, 4)
print(np.round(bert_av_precision, 2))
# 0.78
print(np.round(bert_precision_arr, 2))
# [1.   1.   0.67 1.   0.67 0.33 0.33 0.33 1.   1.   1.   1.  ]

データ数が少ないため信頼度に疑問は残りますが、定量化したことで結果をはっきりと評価できるようになりました。平均点はELMo: 0.61、BERT: 0.78とBERTに軍配が上がりました。文章ごとのポイントを見ると、「権利」の意味の4文はどちらのモデルもすべて満点となっており、「右」の意味の4文はBERTが高得点を出しているのがわかります。「正しい」の意味の4文はどちらのモデルも苦戦していますが、こちらは平均するとELMoのほうが良い結果を出しています。

ベクトルを取り出す層の比較

ここまで示した結果では、ELMoはLSTMの２層目、BERTは最後から２層目から取り出した埋め込みベクトルを使っていました。最後に、ベクトルを取り出す層によって精度がどう変わるかを見てみます。

ELMo

ELMoから出力される単語ベクトルとしては、文脈に依存しない埋め込み層 word_emb、LSTM１層目 lstm_outputs1、LSTM２層目 lstm_outputs2とそれら３つの平均のELMoベクトルelmoの４種類があります。word_embに関しては、どの文章であっても"right"の単語ベクトルは同じものになりますので、多義語を見分けることはできません。残りの文脈に依存したベクトル

elmo_vectors_e = extract_elmo_vectors(elmo_embeddings_dict, tokens, 'right', 'elmo')
elmo_vectors_1 = extract_elmo_vectors(elmo_embeddings_dict, tokens, 'right', 'lstm_outputs1')
elmo_vectors_2 = extract_elmo_vectors(elmo_embeddings_dict, tokens, 'right', 'lstm_outputs2')

に対して、適合率の平均をそれぞれ求めた結果は以下の通りです。

層	適合率平均
LSTM1層目	0.67
LSTM2層目	0.61
ELMo	0.64

原論文によると２層目のほうが意味的な情報を捉える傾向があるとのことなので、２層目のほうが精度が高くなると予想していたのですが、１層目のほうが精度が良いという結果になりました。12文しかない小さなデータセットの結果なので確定的なことは言えませんが、同義語を見分けるには文章の構造を見ることも大事ということでしょうか。ELMoベクトルの結果がLSTM1層目よりも悪いのは、ELMoベクトルには文脈に依存しないベクトルも加えられていることを考えれば妥当なところでしょう。

BERT

BERT_baseはTransformer12層からなりますので、12層すべてを比較してみます。出力ファイルright_output.jsonlにはすべての層の出力を保存していましたので、以下のようにベクトルを取り出せます。さらに、すべての層の平均ベクトルと最後の6層の平均ベクトルもそれぞれ計算します。

bert_vectors_list = []
for i in range(12):
  bert_vectors_list.append(extract_bert_vectors('./right_output.jsonl', target_layer=i, target_token='right'))

# average of all the layers
bert_vector_av_all = np.mean(bert_vectors_list, axis=0)
# average of the last 6 layers
bert_vector_av_last6 = np.mean(bert_vectors_list[6:], axis=0)

これらのベクトルに対して適合率の平均を求めた結果は以下の通りです。

層	適合率平均
1層目	0.58
2層目	0.67
3層目	0.78
4層目	0.83
5層目	0.83
6層目	0.83
7層目	0.81
8層目	0.78
9層目	0.83
10層目	0.81
11層目	0.78
12層目	0.75
全層平均	0.81
最終6層平均	0.83

入力に近い浅い層や、事前学習タスクに強く影響を受けている最終層（12層目）の精度が低いのは納得のいく結果ではないでしょうか。最高精度は中央付近のいくつかの層と、最終6層の平均のベクトルが達成しています。最高精度どうしで比較しても、BERTがELMoを大きく引き離す結果となりました。

おわりに

ELMoやBERTは文脈を考慮した単語分散表現を与えると言われているものの、このような実験を見たことがなかったので記事にまとめてみました。ここで試した例に関しては、ELMoもBERTもある程度は文脈を捉えて多義語を区別できるという結果となりました。ELMoとBERTの比較では、やはりBERTのほうが高性能でした。

今回は単語分散表現を取り扱いましたが、実社会での応用を考えると、文章の分散表現のほうが応用範囲が広いと思いますので、次は文章の分散表現を使って何か実験してみたいと思います。