主成分分析を実分析・理論の両面から勉強してみたのでシェアします。
1.主成分分析を理解する ~Rでデータ分析編~
2.主成分分析を理解する ~理論編~
目次
1. 主成分分析とは?
2. Rで実際に分析してみる
3. 参考文献
1. 主成分分析とは
主成分分析(Principle Component Analysis:通称PCA)は多次元のデータを次元圧縮する、多変量解析法の一手法です。
[補足]多次元データって?〜小学生の体力測定データを例に〜
多次元データとは、変数、サンプル数が複数あるデータの事です。
以下の体力測定データでは行が学生(サンプル数)、列が測定種目(変数)になってます。
<小学生の体力測定データ>
| 学生ID | 上体起こし(回) | 握力(kg) | 反復横跳び(点) | 50m走(秒) |
|---|---|---|---|---|
| 1 | 13 | 9 | 31 | 11.2 |
| 2 | 18 | 6 | 33 | 13.9 |
| 3 | 10 | 10 | 19 | 10.4 |
| 4 | 8 | 7 | 28 | 9.9 |
主成分分析における次元圧縮とは?
簡単のため、ここでは2変数のデータを用いて説明します。
<体力測定のデータ(一部)>
| 学生ID | 50m走(秒) | 走り幅跳び(cm) |
|---|---|---|
| 1 | 8.3 | 315 |
| 2 | 7.9 | 393 |
| 3 | 10.1 | 240 |
| 4 | 9.3 | 305 |
| 5 | 8.6 | 330 |
| 6 | 8.8 | 340 |
| 7 | 8.1 | 383 |
| 8 | 8.7 | 334 |
| 9 | 8.2 | 397 |
| 10 | 8.2 | 380 |
2変数なのでとりあえずプロットしてみます。
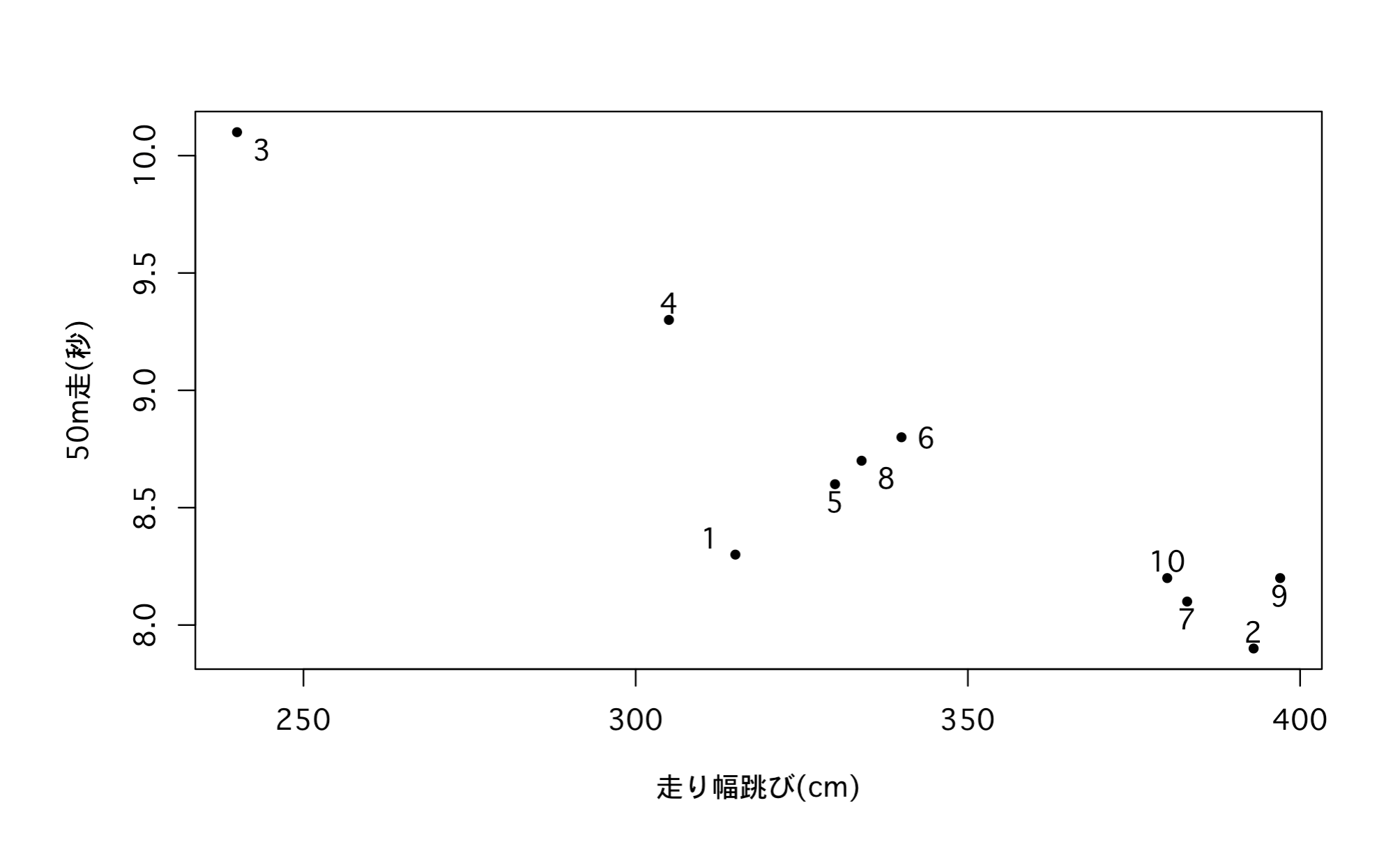
例えば、この散布図から50m走と走り幅跳びの両方の結果をまとめた総合的な能力の指標を求めたいとします。
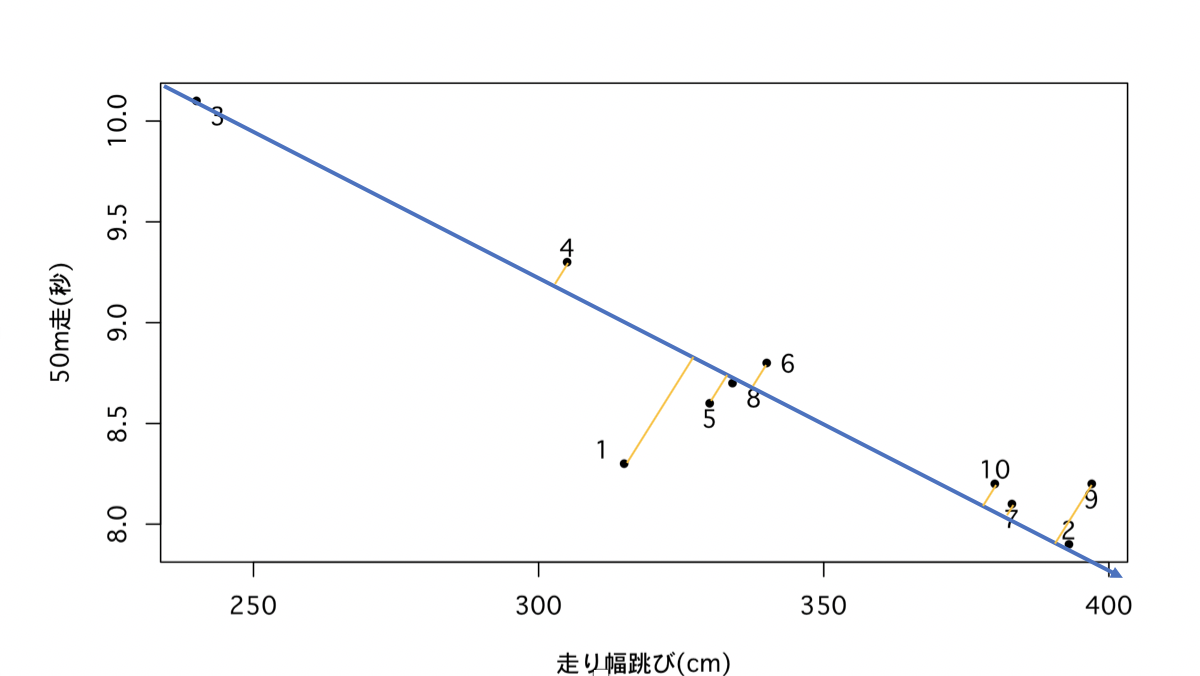
まず、図の青矢印のように有向線分を引きます。
次に、橙線のように各点から有向線分へ線を降ろします。
すると青矢印と橙線の交点が50m走と走り幅跳びを総合した指標の得点になることがわかります。
2変数を青矢印のような1変数にまとめることができました。
この、2変数の情報を出来るだけ保持する総合指標として1変数にまとめる操作のことを2次元から1次元への次元圧縮といいます。
以上のような、多変量のデータの次元をできるだけ情報を損なわずに圧縮して総合指標を作る分析手法が主成分分析です。
2. Rで実際に分析してみる
それでは、主成分分析をRで実行してみましょう。
金先生の教科書に載っているデータは、irisでこれは定量的データ分析ですでに使ったデータなので、今回は以下の本のデータを参考にパイロットの能力テストデータを用いることにします。

「Methods of Multivariate Analysis」
Alvin C. Rencher, William F. Christensen著
書籍リンク:https://www.wiley.com/en-us/Methods+of+Multivariate+Analysis%2C+3rd+Edition-p-9780470178966
参考にしたサイト:https://aaronschlegel.me/principal-component-analysis-r-example.html

データのインポート
以下リンクからpilots.csvファイルをダウンロードしてください。
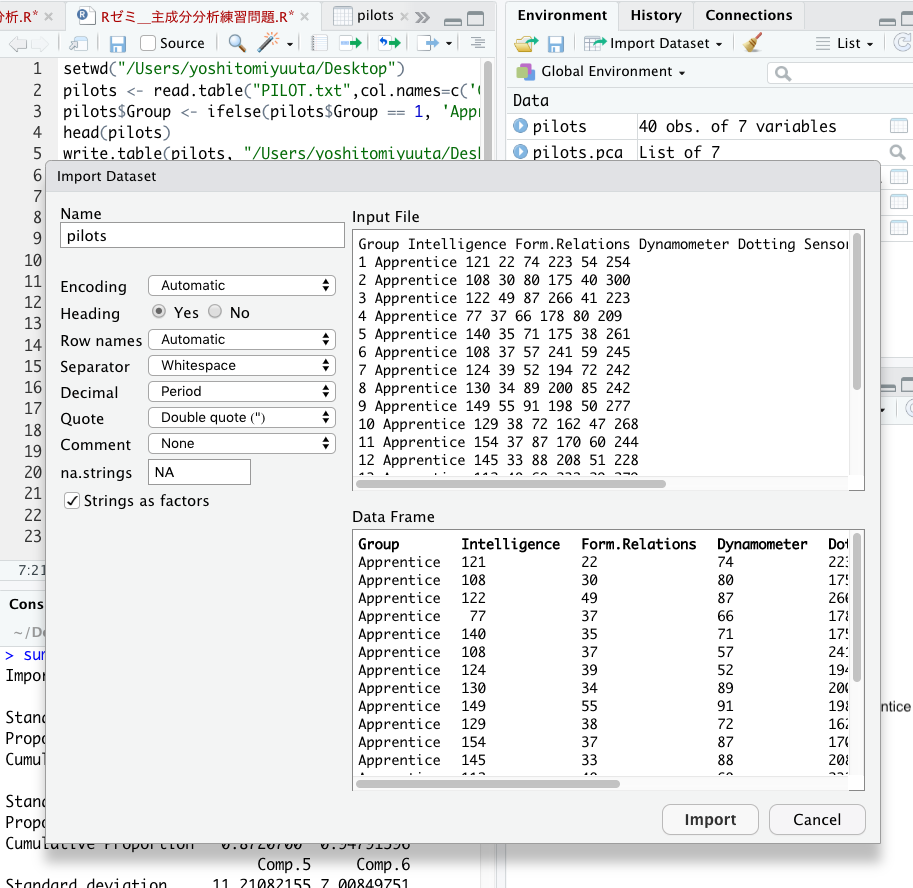
- Rstudioを起動して、画像のようにimport Dataset→From Text(base)からpilots.csvファイルをインポートしてください。
Rstdioの環境構築については以下記事などを参考にしてください。
RとRStudioのインストール
データの概要
20人の見習いエンジニア(Apprentice)と20人のパイロット(Pilot)が6項目のテストを受けたデータ。
テスト項目は以下の6つです。
・Intelligence・・・知能
・Form.Relations・・・人間関係構築
・Dynamometer・・・動力系(ダイナモメーター)の制御
・Dotting・・・紙にペンで点を制限時間内に出来るだけ多く打つテスト
・Sensory.Motor.Coordination・・・センサーとモーターの操作
・Persevation・・・忍耐力
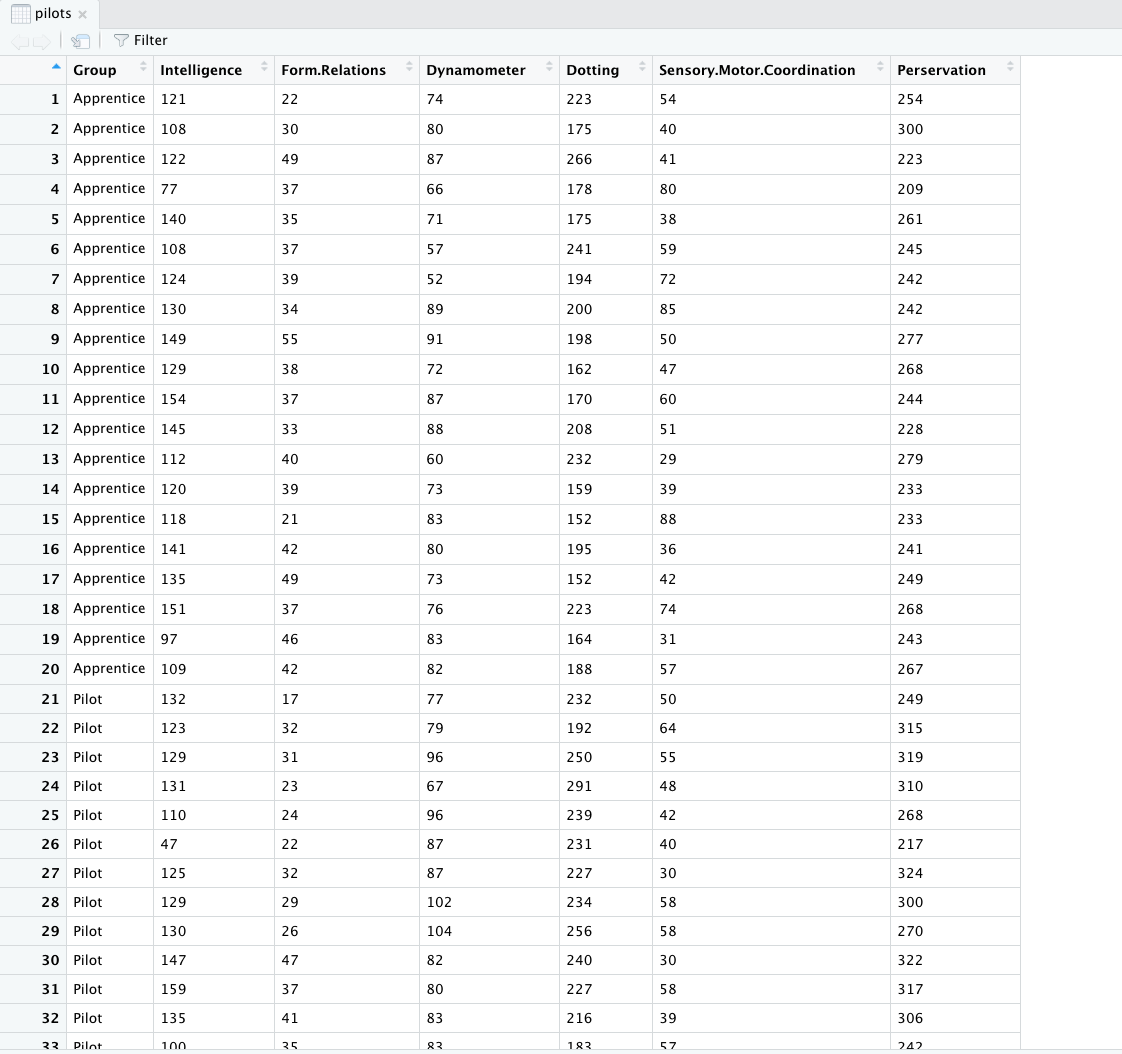
データの一部を**head()**でみてみましょう。
head(pilots)
実行結果
## Group Intelligence Form.Relations Dynamometer Dotting
## 1 Apprentice 121 22 74 223
## 2 Apprentice 108 30 80 175
## 3 Apprentice 122 49 87 266
## 4 Apprentice 77 37 66 178
## 5 Apprentice 140 35 71 175
## 6 Apprentice 108 37 57 241
## Sensory.Motor.Coordination Perservation
## 1 54 254
## 2 40 300
## 3 41 223
## 4 80 209
## 5 38 261
## 6 59 245
主成分分析を実行する
デフォルトで入っているパッケージstatsには主成分分析を行う、関数princompがあります。その書式は以下のようになります。
princomp(x, cor=FALSE, scores=TRUE, ....)
引数xは主成分分析を行うデータフレームです。
主成分分析は分散共分散行列を用いる方法と、相関係数行列を用いる方法があります(詳細は理論面の解説にて後述)。
今回は分散共分散行列(cor=FALSE)を用います。
引数scoresは主成分得点を計算するか否かを指定するものです。TRUEのままで大丈夫です。
pilotsデータに対して主成分分析を実行しましょう。
pilots.pca <- princomp(pilots[,2:7], cor = FALSE)
# 1列目は質的変数なので、2〜7列目を指定する
# 分散共分散行列を用いる
**summary()**で主成分の寄与率および累積寄与率をみてみましょう。
summary(pilots.pca)
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## Standard deviation 40.9754966 29.2642937 ##19.7838975 15.95462346 11.21082155 7.00849751
## Proportion of Variance 0.5002739 0.2551734 ##0.1166227 0.07584597 0.03744848 0.01463556
## Cumulative Proportion 0.5002739 0.7554473 ##0.8720700 0.94791596 0.98536444 1.00000000
Proportion of Variance・・・寄与率を表します。寄与率とは各主成分軸(Comp1など)がデータの何割を説明できているかを表したものです。
Cumulative Proportion・・・累積寄与率を表します。累積寄与率はそれまでの主成分軸の合計でデータの何割を説明できているかを表します。
今回の結果から、第一主成分が**約50%の寄与率、第二主成分が約26%の寄与率であることがわかります。
また第二主成分の累積寄与率は約76%**であるため、第一、第二主成分でデータの約76%を説明できていることがわかります。
分析結果をプロットする
先ほど求めた累積寄与率から第一、第二主成分の2つでデータのかなりの部分を説明できることがわかりました。
次にこの2つの主成分を散布図としてプロットすることで、主成分の特徴などを明らかにしましょう。
まず、最もオーソドックスな**biplot()**で結果をプロットしてみましょう。
biplot(pilots.pca)
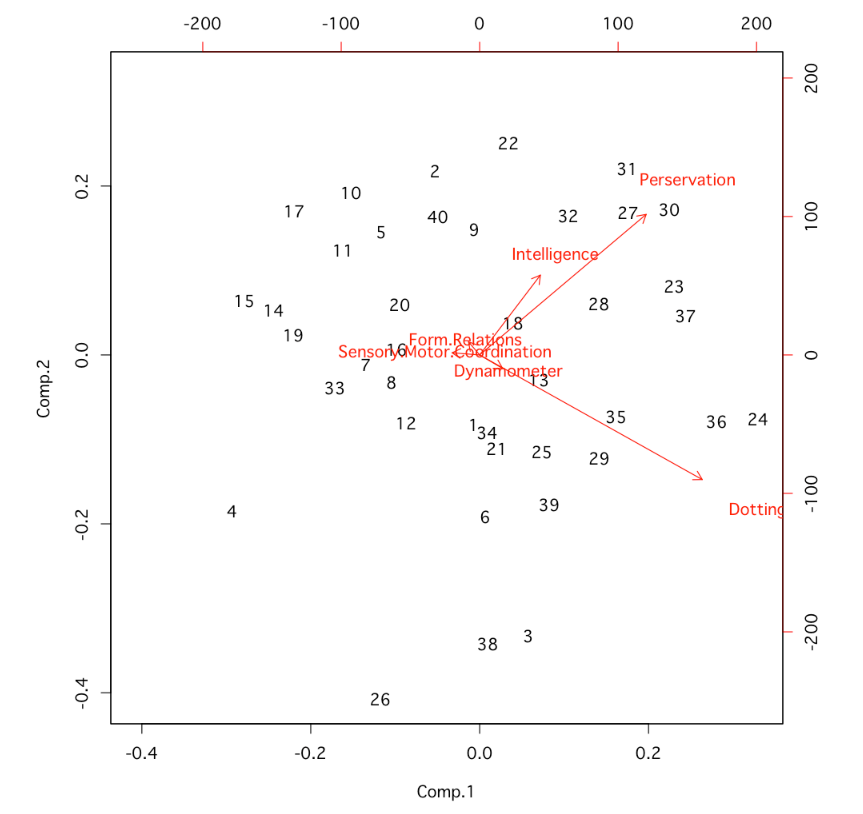
黒い数字が各データの番号を表します。
赤の矢印の向きが2つの主成分に対する各変数の方向を表します。
赤の矢印の長さが各変数が各主成分とどれだけ相関が強いかを表します。
相関が強いほど、矢印は長くなります。
主成分分析の結果を解釈する
主成分の結果から有用な解釈を引き出すためには、プロットした結果をみるのもいいですが、もう一つ有用な方法があります。
データの変数と各主成分の相関を計算することです。やってみましょう。
pilots.pca$loadings
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## Intelligence 0.212 0.389 0.888 0.107
## Form.Relations -0.191 0.148 -0.963
## Dynamometer -0.129 -0.975 -0.124
## Dotting 0.776 -0.608 0.109
## Sensory.Motor.Coordination 0.968 -0.109 -0.203
## Perservation 0.580 0.686 -0.434
数値が空白になっている箇所は近似的にゼロです。
どうでしょうか。プロット結果を見ただけだとあたかも主成分と相関がありそうな変数も実際に相関を計算してみると近似的にゼロ、つまり相関がないことがわかります。(第一主成分におけるDynamometerなど)
グラフをぼんやり見てぼんやり解釈するのは時に危険です。数字を見て考察しましょう。
3.参考文献
Rによるデータサイエンス
S+rescue Chap5 主成分分析
R データフレーム 列の追加
Rでラベル付き散布図を作成して保存するまで
プロットエリア環境設定
Principal Component Analysis with R Example
53.グラフィックスパラメータ(弐)
主成分分析の考え方
Methods of Multivariate Analysis
ggbiplot
意味がわかる主成分分析
Qiitaの数式チートシート