主成分分析を実分析・理論の両面から勉強してみたのでシェアします。
1.主成分分析を理解する ~Rでデータ分析編~
2.主成分分析を理解する ~理論編~
主成分分析の理論を解説
この記事では主成分分析の理論面について解説していきます。
今回は以下の本を参考にしています。

「多変量解析法入門」
永田靖, 棟近雅彦 著
詳細:http://www.saiensu.co.jp/?page=book_details&ISBN=ISBN4-7819-0980-9
相関係数行列を用いた主成分分析
1.主成分分析を理解する ~Rでデータ分析編~では、分散共分散行列を用いて主成分分析を行いました。
しかし、データの各変数の単位が異なる場合、分散共分散行列は各単位の影響を受けてしまいます。それは分散、共分散の定義から明らかです。
分散
S_{xx}=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2
共分散
S_{xy}=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})
そこで分散共分散行列の代わりに相関係数行列を用いることで、各変数の単位の影響を受けずに分析ができます。
相関係数の定義からも明らかです。
相関係数
R_{xy}=\frac{S_{xy}}{S_{x}S_{y}}=\frac{\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2}\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i-\bar{y})^2}}
以上より、データの各変数の単位が異なることが明らかな場合、または各変数の単位について十分な知識がない場合、主成分分析において分散共分散行列よりも相関係数行列を用いたほうが無難です。
以下では、相関係数行列を用いた主成分分析について解説します。
主成分分析の解析ストーリー
Ⅰ. 相関係数行列Rの第1固有値(最大固有値) $\lambda_1$に対応する固有ベクトルから第1主成分 $z_1$を求めます。次に、Rの第2固有値 $\lambda_2$に対応する第2主成分 $z_2$を求めます。同様にして第k主成分を求めます。($k=3,4,...,p$)
Ⅱ. それぞれの主成分の寄与率および累積寄与率を求めます。
Ⅲ. 因子負荷量を求めます。因子負荷量を散布図にプロットすることで、変数の分類を行います。
Ⅳ. 主成分得点を散布図にプロットし、サンプルの特徴づけや分類を行います。
主成分分析の流れは上記のようになります。
以下、簡単のため変数が $x_1$, $x_2$の2つで、サンプルサイズがn個の場合について具体的に解説していきます。
Ⅰ. 主成分の導出
まず、変数$x_1$, $x_2$を標準化します。$s_1$,$s_2$は$x_1$,$x_2$の標準偏差です。
u_1=\frac{x_1-\bar{x_1}}{s_1},\hspace{5mm}u_2=\frac{x_2-\bar{x_2}}{s_2}\hspace{10mm}(1.1)
後のため、以下の式を導出しておきます。
\sum_{i=1}^{n}{u_{i1}}^2=\sum_{i=1}^{n}{u_{i2}}^2=n-1\hspace{10mm}(1.2)
\sum_{i=1}^{n}{u_{i1}}{u_{i2}}=(n-1)r_{x_1x_2}\hspace{10mm}(1.3)
(1.2)と(1.3)の証明については時間の都合上説明はしませんが、以下のようになります。
原先生の講義と同じく、分散を$n$ではなく$n-1$で割るものと定義しています。
余談にはなりますが、その理由などは以下リンクなど参照してください。
分散は n で割るか n − 1 で割るか
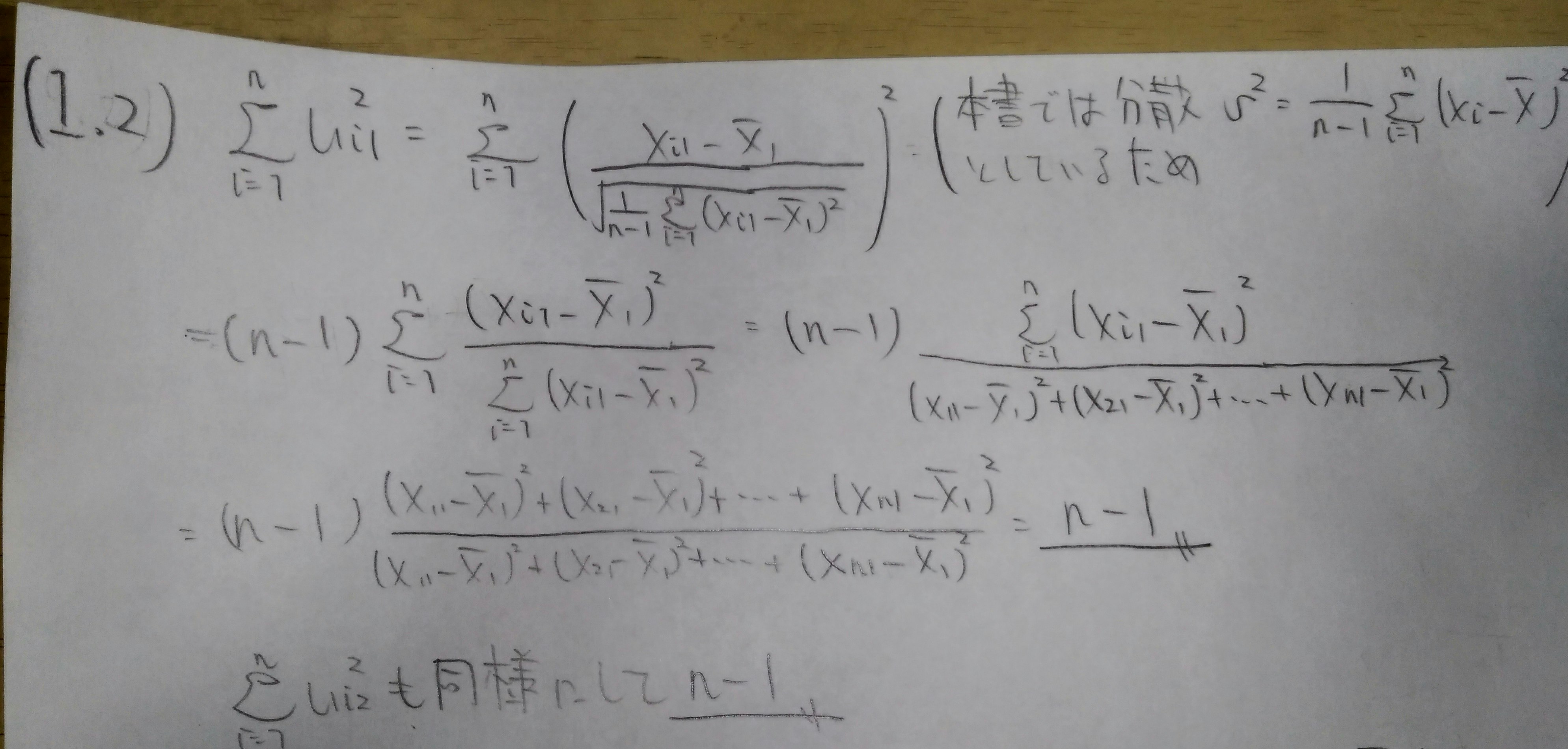
第1主成分$z_1$を
z_1=a_1u_1+a_2u_2\hspace{10mm}(1.4)
とおきます。$\bar{u_1}=\bar{u_2}=0$より、
\bar{z_1}=0\hspace{10mm}(1.5)
主成分導出の目的はデータの情報をできるだけ多く有するように$z_1$を求めることです(つまり係数$a_1$と$a_2$をデータから定めることです)。
**「${z_1}$がもとのデータの情報をできるだけ多く有する」→「データの全体のバラツキ(分散)をできるだけ$z_1$のバラツキ(分散)に反映させる」**と考えます。
$z_1$の分散は
V_{z1}=\frac{1}{n-1}\sum_{i=1}^{n}(z_{i1}-\bar{z_1})^2
(1.5)より、$\bar{z_1}=0$であるから
V_{z1}=\frac{1}{n-1}\sum_{i=1}^{n}z_{i1}^2\hspace{10mm}(1.6)
この$V_{z1}$が最大になるような$a_1$と$a_2$を求める。(1.4)より
V_{z1}=\frac{1}{n-1}\sum_{i=1}^{n}z_{i1}^2=\frac{1}{n-1}\sum(a_1u_1+a_2u_2)^2
2乗の部分を展開します。
V_{z1}=\frac{1}{n-1}(a_1^2\sum{u_{i1}^2}+2a_1a_2\sum{u_{i1}u_{i2}}+a_2^2\sum{u_{i2}^2})
(1.2)と(1.3)を用いて
V_{z1}=a_1^2+a_2^2+2r_{x_1x_2}a_1a_2\hspace{10mm}(1.7)
となるため$V_{z1}$の値は$(a_1, a_2)$の値が大きくなればいくらでも大きくなります。
そこで、
a_1^2+a_2^2=1
の制約条件を設けた下で、$V_{z1}$の最大化を考えましょう。
制約付きの最大化問題を求めるための定石はラグランジュの未定乗数法です。
未定乗数$\lambda$を用いて、
f(a_1,a_2,\lambda)=a_1^2+a_2^2+2r_{x_1x_2}a_1a_2-\lambda(a_1^2+a_2^2-1)\hspace{10mm}(1.9)
とおき、$a_1$,$a_2$のそれぞれで偏微分してゼロと置く、すると次式のようになります。
\begin{align}
2a_1&+2r_{x_1x_2}a_2&-2\lambda a_1&=0\hspace{10mm}(1.10a)\\
2r_{x_1x_2}a_1&+\hspace{11mm}2a_2&-2\lambda a_2&=0\hspace{10mm}(1.10b)
\end{align}
偏微分する過程については説明はしませんが以下のようになります。
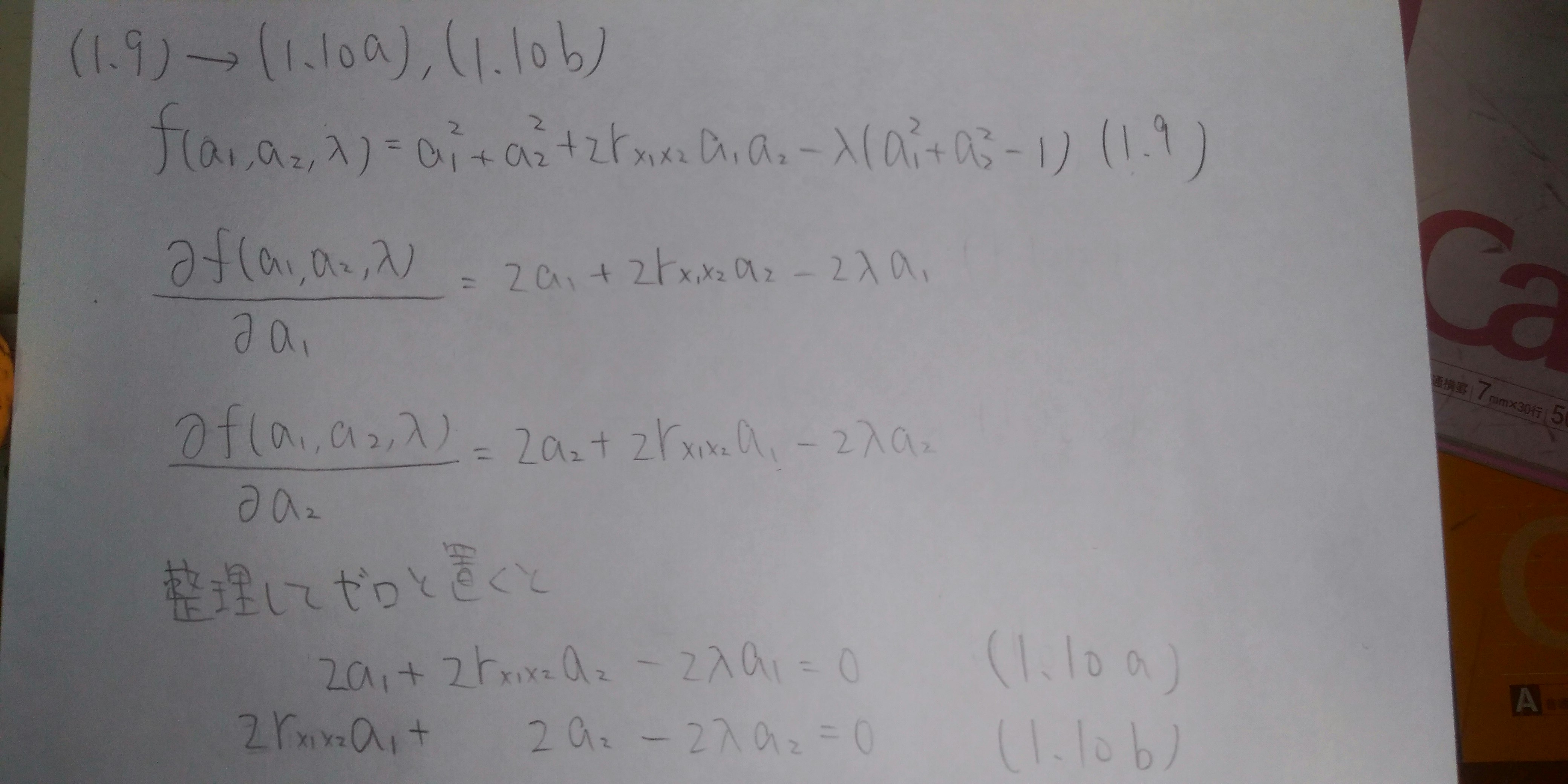
(1.10a),(1.10b)の両辺をそれぞれ2で割って、行列の式に表現すると
\begin{bmatrix}1&r_{x_1x_2}\\r_{x_1x_2}&1\end{bmatrix}\begin{bmatrix}a_1\\a_2\end{bmatrix}=\lambda\begin{bmatrix}a_1\\a_2\end{bmatrix}\hspace{10mm}(1.11)
となる。相関係数行列$R$を
R=\begin{bmatrix}1&r_{x_1x_2}\\r_{x_1x_2}&1\end{bmatrix}\hspace{10mm}(1.12)
とおく、また$a=[a_1,a_2]'$とおくと、(1.11)は
Ra=\lambda a\hspace{10mm}(1.13)
となります。(1.11)および、(1.13)は$\lambda$が行列$R$の固有値であり、求めるべき$[a_1,a_2]$は固有ベクトルであることがわかります。
ここで、(1.11)の両辺に左からベクトル$[a_1, a_2]$をかけてみます。すると
a_1^2+a_2^2+2r_{x1x2}a_1a_2=\lambda(a_1^2+a_2^2)
を得ます。(1.7)よりこの式の左辺は$V_{z1}$であり、右辺は(1.8)でも受けた制約条件より$\lambda$に等しいです。
よって
V_{z1}=\lambda
であることが導かれます。
したがって(1.7)の$V_{z1}$を最大化することは
「相関係数行列Rの固有値問題を解いて、最大固有値 $\lambda_1$に対応する(長さ1の)固有ベクトル$a=[a_1,a_2]'$を求めればそれが$V_{z1}$の最大値を与える$[a_1,a_2]$であり、$V_{z1}$の最大値を $\lambda_1$とする。」
上記の手続きを踏むことで実行できます。
よって、$V_{z1}$を最大にする、固有ベクトル$a=[a_1,a_2]'$を求め第一主成分を求めてみましょう。
相関係数行列$R$は
R=\begin{bmatrix}1&r\\r&1\end{bmatrix}
です。$R$の固有値は、
\begin{vmatrix}1-\lambda&r\\r&1-\lambda\end{vmatrix}=(1-\lambda)^2-r^2=0
を解くことで
\lambda_1=1+r,\hspace{5mm}\lambda_2=1-r
となり、第一主成分の場合は最大固有値$\lambda_1$を用います。
$\lambda_1$に対応する固有ベクトルは
a=[\sqrt{2}/2,\hspace{1mm}\sqrt{2}/2]'
であり、第一主成分$z_1$は以下のようになります。
z_1=\frac{\sqrt{2}}{2}u_1+\frac{\sqrt{2}}{2}u_2
今回は省略しますが、同様に第二主成分も求めることができます。
z_2=\frac{\sqrt{2}}{2}u_1-\frac{\sqrt{2}}{2}u_2
[補足]主成分の選択基準について
データを説明する主成分はいくつ選択すればいいのかについて、目安を示しておきます。
1.各主成分に対応する固有値が1以上
または
2.累積寄与率が80%を超える
になります。
Ⅱ. 寄与率および累積寄与率
寄与率の定義は以下のようになります。
第一主成分の寄与率
\frac{\lambda_1}{\lambda_1+\lambda_2}
第二主成分の寄与率
\frac{\lambda_2}{\lambda_1+\lambda_2}
累積寄与率の定義は以下のようになります。
変数は2つなので第二主成分の累積寄与率は1となります。
第一主成分の累積寄与率
\frac{\lambda_1}{\lambda_1+\lambda_2}
第二主成分の累積寄与率
\frac{\lambda_1+\lambda_2}{\lambda_1+\lambda_2}=1
Ⅲ. 因子負荷量と主成分の解釈
主成分と元の変数$x_1$,$x_2$との相関係数$[r_{z_1x_1},r_{z_1x_2}, r_{z_2x_1}, r_{z_2x_2}]$を因子負荷量と呼びます。
Ⅳ. 主成分得点
個々のサンプルに対して各変数の値を標準化して(1.4)に代入して得られた値を第一主成分の主成分得点と呼びます。第二主成分も同様にして主成分得点を求めることができます。
z_1=a_1u_1+a_2u_2\hspace{10mm}(1.4)
各主成分に対して、主成分得点はサンプルの個数だけ計算できます。これらを散布図にプロットし、サンプルの特徴付けや分類などを試みます。
補足として、Ⅰ.主成分の導出の第一主成分の分散を求める過程で使用したラグランジュの未定乗数法については、ラグランジュの未定乗数法チュートリアルを参考にしてください。


