目次
1.Prophetで日経平均株価を予測 #1 ~Prophetモデルでとりあえず予測してみた~
2.Prophetで日経平均株価を予測 #2 ~株価を対数収益率に変換しモデリング~
やったこと
時系列解析ライブラリProphetを用いて株価を予測する精度を上げるために、株価を対数収益率に変換した。そして、対数収益率モデルのデータへの当てはまり具合を検証した。
前回の記事で作成したモデルの振り返り
Prophetで日経平均株価を予測 #1 ~Prophetモデルでとりあえず予測してみた~
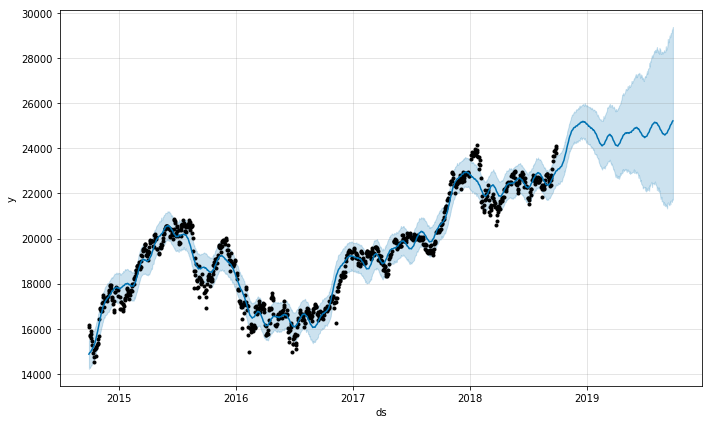
↑の記事で5年分の株価データをつかってそのままProphetモデルを作成してみたところ、日経平均は今後上昇し続けるという結果が出た。しかし、現実は日経平均は2018年11月8日現在22,486.92円と停滞している。また、モデルの誤差の範囲も大きく、このモデルを使って日経平均を予測するのは不可能と判断した。以下は前回作成した予測モデル。
対数収益率とは
株価を対数収益率に変換する前に、対数収益率について解説する。
収益率の対数をとったものが対数収益率。収益率とは、株価が日ごとにどれくらい変化したかを表したもの。$F_t$をある日$t$の終値だとすると、対数収益率は以下の式のようになる。$$\log(\frac{F_t}{F_{t-1}})$$対数表示でなく、パーセント表示ならば$$100(\frac{F_t}{F_{t-1}}-1)$$
パーセント収益率ではなく対数収益率を用いるメリット
- 対数収益率は加算可能であるため、5日分の収益などを計算しやすい
- 利益と損失に関して対照的。例えば、株価が50%増加したときは-0.5の株価収益率になりますが、この後200%増加した場合、2.0の株価収益率になる。したがってパーセント収益率では同じ量の利益/損失であっても値の絶対値が異なる。これを対数収益率で表現すると$\log(0.5)=-0.301$、$\log(2.0)=0.301$となり、利益と損失が対照的になる。
日経平均株価の対数収益率をモデリングする
対数収益率を使うことによるメリットは、上で述べたこと以外にもある。対数収益率はデータの範囲がほぼ0~1の範囲に収まるため、普通に株価をモデリングしたときよりも残差が小さくなる。したがって、予測モデルの当てはまりがよくなり、予測精度が向上につながる。今回の記事では、対数収益率をモデリングした場合と株価をそのままモデリングした場合で両モデルの当てはまりを比較していく。
開発環境
言語: Python 3.6.5
フレームワーク: Jupyter Notebook
OS: Windows 10
サンプルコードは以下
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from fbprophet import Prophet
from fbprophet.diagnostics import cross_validation
from fbprophet.diagnostics import performance_metrics
from fbprophet.plot import plot_cross_validation_metric
data = pd.DataFrame()
file_name = 'N225'
data2 = pd.read_csv(file_name, skiprows=1, header=None, names=['ds','Open','High','Low','Close','Adj_Close','Volume'])
data3 = data2.dropna(how='any')
data = data.append(data3)
print(data)
plt.style.use('ggplot')
fig = plt.figure(figsize=(18,8))
ax_Nikkei = fig.add_subplot(224)
ax_Nikkei.plot(data.loc["1965-01-05": ,['Adj_Close']], label='Nikkei', color='r')
ax_Nikkei.set_title('NIKKEI225')
data['Adj_Close_log'] = np.log(data.Adj_Close).diff()
data.head()
data.tail()
fig = plt.figure(figsize=(18,8))
ax_Nikkei_log = fig.add_subplot(224)
ax_Nikkei_log.plot(data.loc["1965-01-05": ,['Adj_Close_log']], label='log diff', color='b')
ax_Nikkei_log.set_title('log earning rate')
model = Prophet()
model.fit(data.rename(columns={'Adj_Close':'y'}))
future_data = model.make_future_dataframe(periods=365, freq= 'd')
forecast_data = model.predict(future_data)
fig = model.plot(forecast_data)
df_cv = cross_validation(model, initial='730 days', period='180 days', horizon = '365 days')
df_cv.head()
df_p = performance_metrics(df_cv)
df_p.head()
def plot_cross_validation_metric(
df_cv, metric, rolling_window=0.1, ax=None, figsize=(10, 6)
):
"""Plot a performance metric vs. forecast horizon from cross validation.
Cross validation produces a collection of out-of-sample model predictions
that can be compared to actual values, at a range of different horizons
(distance from the cutoff). This computes a specified performance metric
for each prediction, and aggregated over a rolling window with horizon.
This uses fbprophet.diagnostics.performance_metrics to compute the metrics.
Valid values of metric are 'mse', 'rmse', 'mae', 'mape', and 'coverage'.
rolling_window is the proportion of data included in the rolling window of
aggregation. The default value of 0.1 means 10% of data are included in the
aggregation for computing the metric.
As a concrete example, if metric='mse', then this plot will show the
squared error for each cross validation prediction, along with the MSE
averaged over rolling windows of 10% of the data.
Parameters
----------
df_cv: The output from fbprophet.diagnostics.cross_validation.
metric: Metric name, one of ['mse', 'rmse', 'mae', 'mape', 'coverage'].
rolling_window: Proportion of data to use for rolling average of metric.
In [0, 1]. Defaults to 0.1.
ax: Optional matplotlib axis on which to plot. If not given, a new figure
will be created.
Returns
-------
a matplotlib figure.
"""
if ax is None:
fig = plt.figure(facecolor='w', figsize=figsize)
ax = fig.add_subplot(111)
else:
fig = ax.get_figure()
# Get the metric at the level of individual predictions, and with the rolling window.
df_none = performance_metrics(df_cv, metrics=[metric], rolling_window=0)
df_h = performance_metrics(df_cv, metrics=[metric], rolling_window=rolling_window)
# Some work because matplotlib does not handle timedelta
# Target ~10 ticks.
tick_w = max(df_none['horizon'].astype('timedelta64[ns]')) / 10.
# Find the largest time resolution that has <1 unit per bin.
dts = ['D', 'h', 'm', 's', 'ms', 'us', 'ns']
dt_names = [
'days', 'hours', 'minutes', 'seconds', 'milliseconds', 'microseconds',
'nanoseconds'
]
dt_conversions = [
24 * 60 * 60 * 10 ** 9,
60 * 60 * 10 ** 9,
60 * 10 ** 9,
10 ** 9,
10 ** 6,
10 ** 3,
1.,
]
for i, dt in enumerate(dts):
if np.timedelta64(1, dt) < np.timedelta64(tick_w, 'ns'):
break
x_plt = df_none['horizon'].astype('timedelta64[ns]').astype(np.int64) / float(dt_conversions[i])
x_plt_h = df_h['horizon'].astype('timedelta64[ns]').astype(np.int64) / float(dt_conversions[i])
ax.plot(x_plt, df_none[metric], '.', alpha=0.5, c='gray')
ax.plot(x_plt_h, df_h[metric], '-', c='b')
ax.grid(True)
ax.set_xlabel('Horizon ({})'.format(dt_names[i]))
ax.set_ylabel(metric)
return fig
fig = plot_cross_validation_metric(df_cv, metric='mse')
model2 = Prophet()
model2.fit(data.rename(columns={'Adj_Close_log':'y'}))
future_data2 = model2.make_future_dataframe(periods=365, freq= 'd')
forecast_data2 = model2.predict(future_data2)
fig2 = model2.plot(forecast_data2)
df_cv2 = cross_validation(model2, initial='730 days', period='180 days', horizon = '365 days')
df_cv2.head()
df_p2 = performance_metrics(df_cv2)
df_p2.head()
fig = plot_cross_validation_metric(df_cv2, metric='mse')
以下サンプルコードを詳しく説明
必要なライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from fbprophet import Prophet
from fbprophet.diagnostics import cross_validation
from fbprophet.diagnostics import performance_metrics
from fbprophet.plot import plot_cross_validation_metric
・numpy・・・数値計算を効率的に行うためのライブラリ。
・pandas・・・csv形式のデータをPython上でデータフレームとして扱うために必要なライブラリ。
・matplotlib.pyplot・・・Pythonでデータを分析した結果をグラフで表示するためのライブラリ。
・Prophet・・・Pythonで時系列解析を実装できるFacebookが開発したライブラリ(pipでインストールが必要)
$ pip install fbprophet
これでインストールできない場合、以下リンクなどを参考にしてください.
https://github.com/facebook/prophet/issues/201
・cross_validation・・・データに対してCV(交差検証)を実行するライブラリ
・performance_metrics・・・予測モデルのパフォーマンスを示す値をまとめた表を出力するライブラリ。
・plot_cross_validation_metric・・・CV(交差検証)のパフォーマンスを示す値をまとめた表を出力するライブラリ。
日経平均株価データのダウンロード
日経平均株価データはYAHOO!FINANCEのWebサイトからダウンロード可能。
リンク:https://finance.yahoo.com/quote/%5EN225/history?ltr=1
取得したい期間を自由に指定してcsv形式でダウンロード。
今回は1965/1/05~2018/11/02の取得可能な全期間のデータを使う。
データをJupyter Notebookに取り込む
data = pd.DataFrame()
file_name = 'N225'
data2 = pd.read_csv(file_name, skiprows=1, header=None, names=['ds','Open','High','Low','Close','Adj_Close','Volume']) #日付データはdsと定義
data3 = data2.dropna(how='any') #欠損値を除去
data = data.append(data3)
print(data)
padasを用いて空のデータフレームを定義
次に先ほどダウンロードしたデータをfile_nameに格納
格納しただけではProphetで予測モデルを作成できないので、names=でデータの変数名を再定義
Prophetで扱う日付データはdsと定義
drop.na()で欠損値を除去
日経平均株価をプロットする
plt.style.use('ggplot')
fig = plt.figure(figsize=(18,8))
ax_Nikkei = fig.add_subplot(224)
ax_Nikkei.plot(data.loc["1965-01-05": ,['Adj_Close']], label='Nikkei', color='r') #調整済み終値をプロット、色は赤を指定
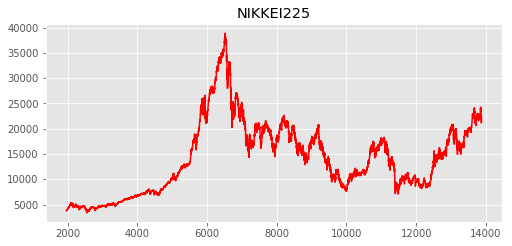
ax_Nikkei.set_title('NIKKEI225') #タイトルをNIKKEI225と指定
プロットには時系列データ解析のメモ+pythonで株価の取得を参考にさせていただいた。
株価の対数収益率を計算しプロット
data['Adj_Close_log'] = np.log(data.Adj_Close).diff()
data.head()
data.tail()
fig = plt.figure(figsize=(18,8))
ax_Nikkei_log = fig.add_subplot(224)
ax_Nikkei_log.plot(data.loc["1965-01-05": ,['Adj_Close_log']], label='log diff', color='b')
ax_Nikkei_log.set_title('log earning rate')
差分を計算するdiff()関数を用いて、対数収益率を計算。どうして差分を計算するのかは、収益率の代わりに対数差分を用いられる理由を参照してください。
Adj_Close_logカラムを見ると、株価の値が対数に変換されていることが確認できる。
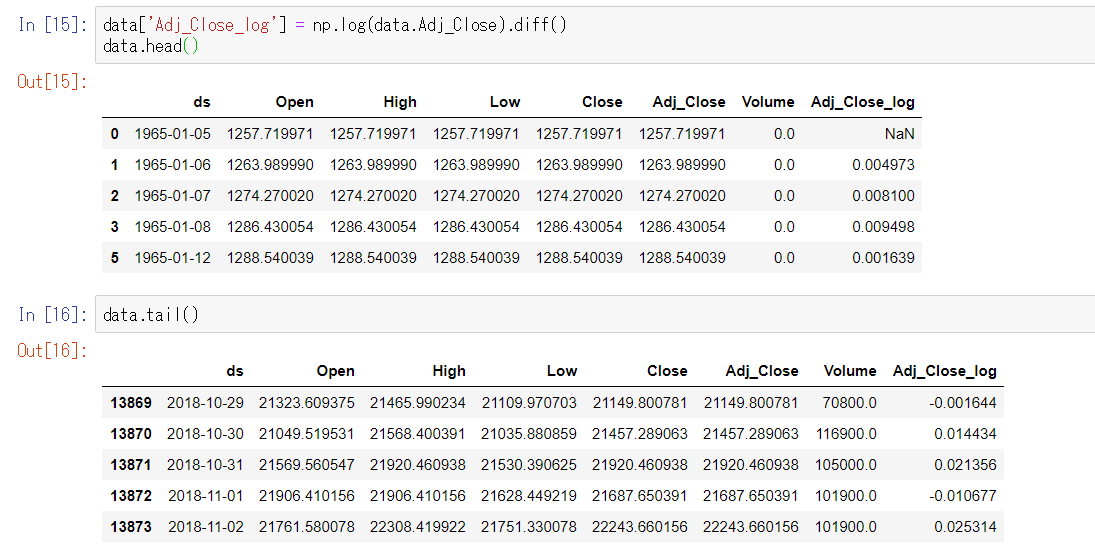
プロットには時系列データ解析のメモ+pythonで株価の取得を参考にさせていただいた。

日経平均の調整済み終値をモデリングする
株価の対数収益率をモデリングする場合と比較するために、日経平均株価をそのまま使うモデルを作成する。
Prophetによるモデリングのプロセスは、Prophetで日経平均株価を予測 #1 ~Prophetモデルでとりあえず予測してみた~と同じなので説明は省略。
model = Prophet()
model.fit(data.rename(columns={'Adj_Close':'y'})) #調整済み終値をモデルの目的変数とする
future_data = model.make_future_dataframe(periods=365, freq= 'd')#今後1年分の株価を予測
forecast_data = model.predict(future_data)
fig = model.plot(forecast_data)
青の実線がデータをもとに引いた予測線で、水色の範囲で誤差の範囲を表している。
今回は1965年からの株価データを使っているため、前回より誤差の範囲が小さくなっている。

モデルに対してCV(交差検証)を行う
予測モデルのデータへの当てはまり具合を評価するために、交差検証を行う。詳細は、時系列解析ライブラリProphet 公式ドキュメント翻訳11(モデルの診断編)を参照してください。
df_cv = cross_validation(model, initial='730 days', period='180 days', horizon = '365 days')
df_cv.head()

交差検証の結果の表を一部出力したものが上の表である。
ここから各行の$y-yhat$の値を求めると、実際データと予測モデルが推測した値の誤差(残差)が分かる。
予測モデルのデータへの当てはまり具合をMSE(平均二乗誤差)をプロットして可視化する
作成したモデルを評価する指標として、今回はMSE(平均二乗誤差)をプロットする。
平均二乗誤差とは各データの値$X_i$と、モデルの推定値$C_i$の間の誤差を二乗して平均したもので、以下の式で表せる。$$MSE=\frac{1}{n}\sum_{i=1}^{n}({x_i-c_i})^2$$
以下のコードでplot_cross_validation_metric()を再定義している理由は、プロットの際にバグが出るらしいので、公式のgithubページから修正プログラムをコピペしたためである。
バグについてはTypeError: cannot astype a timedelta from [timedelta64[ns]] to [int32] #593を参照してください。
df_p = performance_metrics(df_cv)
df_p.head()
# MSEをプロットする関数をデバッグのために再定義
def plot_cross_validation_metric(
df_cv, metric, rolling_window=0.1, ax=None, figsize=(10, 6)
):
"""Plot a performance metric vs. forecast horizon from cross validation.
Cross validation produces a collection of out-of-sample model predictions
that can be compared to actual values, at a range of different horizons
(distance from the cutoff). This computes a specified performance metric
for each prediction, and aggregated over a rolling window with horizon.
This uses fbprophet.diagnostics.performance_metrics to compute the metrics.
Valid values of metric are 'mse', 'rmse', 'mae', 'mape', and 'coverage'.
rolling_window is the proportion of data included in the rolling window of
aggregation. The default value of 0.1 means 10% of data are included in the
aggregation for computing the metric.
As a concrete example, if metric='mse', then this plot will show the
squared error for each cross validation prediction, along with the MSE
averaged over rolling windows of 10% of the data.
Parameters
----------
df_cv: The output from fbprophet.diagnostics.cross_validation.
metric: Metric name, one of ['mse', 'rmse', 'mae', 'mape', 'coverage'].
rolling_window: Proportion of data to use for rolling average of metric.
In [0, 1]. Defaults to 0.1.
ax: Optional matplotlib axis on which to plot. If not given, a new figure
will be created.
Returns
-------
a matplotlib figure.
"""
if ax is None:
fig = plt.figure(facecolor='w', figsize=figsize)
ax = fig.add_subplot(111)
else:
fig = ax.get_figure()
# Get the metric at the level of individual predictions, and with the rolling window.
df_none = performance_metrics(df_cv, metrics=[metric], rolling_window=0)
df_h = performance_metrics(df_cv, metrics=[metric], rolling_window=rolling_window)
# Some work because matplotlib does not handle timedelta
# Target ~10 ticks.
tick_w = max(df_none['horizon'].astype('timedelta64[ns]')) / 10.
# Find the largest time resolution that has <1 unit per bin.
dts = ['D', 'h', 'm', 's', 'ms', 'us', 'ns']
dt_names = [
'days', 'hours', 'minutes', 'seconds', 'milliseconds', 'microseconds',
'nanoseconds'
]
dt_conversions = [
24 * 60 * 60 * 10 ** 9,
60 * 60 * 10 ** 9,
60 * 10 ** 9,
10 ** 9,
10 ** 6,
10 ** 3,
1.,
]
for i, dt in enumerate(dts):
if np.timedelta64(1, dt) < np.timedelta64(tick_w, 'ns'):
break
x_plt = df_none['horizon'].astype('timedelta64[ns]').astype(np.int64) / float(dt_conversions[i])
x_plt_h = df_h['horizon'].astype('timedelta64[ns]').astype(np.int64) / float(dt_conversions[i])
ax.plot(x_plt, df_none[metric], '.', alpha=0.5, c='gray')
ax.plot(x_plt_h, df_h[metric], '-', c='b')
ax.grid(True)
ax.set_xlabel('Horizon ({})'.format(dt_names[i]))
ax.set_ylabel(metric)
return fig
fig = plot_cross_validation_metric(df_cv, metric='mse')#MSEをプロット
MSEを可視化した結果は以下。

青線がMSEである。ここから、おおむねMSEは$0.3×10^8=30000000$であるといえる。日経平均株価をそのままモデリングすると、とんでもなくMSEが高くなり当てはまりの悪いモデルになることが分かる。
次に株価ではなく対数収益率をモデリングしてMSEをプロットする。プロセスは同様なので省略。
対数収益率をモデリング、MSEをプロットする
model2 = Prophet()
model2.fit(data.rename(columns={'Adj_Close_log':'y'}))
future_data2 = model2.make_future_dataframe(periods=365, freq= 'd')
forecast_data2 = model2.predict(future_data2)
fig2 = model2.plot(forecast_data2)
df_cv2 = cross_validation(model2, initial='730 days', period='180 days', horizon = '365 days')
df_cv2.head()
df_p2 = performance_metrics(df_cv2)
df_p2.head()
fig = plot_cross_validation_metric(df_cv2, metric='mse')
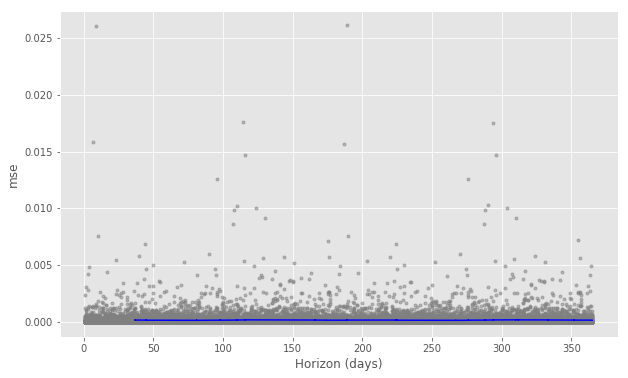
モデリングの結果。対数収益率に直したことで、縦軸の値が非常に小さくなっている。

青線で可視化されたMSEをみるとおおむね0.001といえる。劇的にMSEが小さくなったことが分かる。
結論
株価をそのままモデリングするんじゃなくて、対数収益率に変換しよう。
今後は、対数収益率のモデルを使って予測値を出したり、ボラティリティを正規化したり、古いデータに対する指数関数的な重みの減少を追加するなどして株価の予測精度を上げていく。
おまけ
今回は評価指標としてMSEを使ったが、本当はMAPE(平均絶対パーセント誤差)のほうがメジャーな指標なので使いたかった。しかし、対数収益率のモデルでMAPEを算出するとMAPEが巨大になるという問題が発生した。
原因は、MAPE(平均絶対パーセント誤差、平均絶対誤差率)とは ~Wikipedia翻訳~にあるように、誤差が非常に小さいことであろう。
参考文献
株式の計量分析入門
データサイエンス講義
In python plots, what dose "le8" mean in reference to the y-axis?
TypeError: cannot astype a timedelta from [timedelta64[ns]] to [int32] #593
Qiitaの数式チートシート
平均二乗誤差
時系列解析ライブラリProphet 公式ドキュメント翻訳11(モデルの診断編)
MAPE(平均絶対パーセント誤差、平均絶対誤差率)とは ~Wikipedia翻訳~
facebook/prophet
Hourly Time Series forecasting with Prophet
要素の差分、足し合わせを計算するNumPyのdiff関数とcumsum関数の使い方
Prophetで日経平均株価を予測 #1 ~Prophetモデルでとりあえず予測してみた~
収益率の代わりに対数差分を用いられる理由
時系列データ解析のメモ+pythonで株価の取得
<時系列データ解析> 株価をプロット〜Pythonと株価データを使って勉強する〜
Pythonでグラフを表示してみた
pandasで欠損値NaNを除外(削除)・置換(穴埋め)・抽出