やったこと
時系列解析ライブラリProphet 公式ドキュメント翻訳11(モデルの診断編)
↑の記事で取り上げたProphetモデルの評価指標である、MAPE(平均絶対パーセント誤差)のWikipediaを翻訳しました。
MAPEについては日本語のソースが少なかったので、記事にしました。
翻訳元:Mean absolute percentage error
平均絶対パーセント誤差
平均絶対パーセント誤差(MAPE)、別名平均絶対パーセント偏差(MAPD)は、トレンドの推定などの統計学の予測手法の予測精度を測る指標です。通常はパーセントで精度を表現し、以下の式で定義されます。
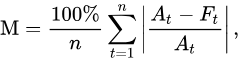
$A_t$は実測値で、$F_t$は予測値です。$A_t$と$F_t$の差を$A_t$で割ります。この計算の絶対値を求め、すべての予測点について絶対値を求めていきます。そしてそれらを合計し、予測値の数$n$で割ります。最後に100を乗じることでパーセント単位にします。
MAPEの概念はとてもシンプルで納得のいくものに思えますが、実際に使う場合は目立つ欠点がいくつかあります[1]。
- 0がデータに存在する場合、使えません。(需要データを扱う場合など、しばしば起こります。)ゼロで割ることになってしまうためです。
- 予測値が小さすぎる場合はパーセント誤差は100%を超えることはありません。しかし予測値が大きすぎる場合は、パーセント誤差は上限がなくなってしまいます。
- 予測精度を比較するメソッドとして使われているMAPEは、系統的には予測値がとても小さい場合に対するメソッドです。その意味でMAPEにはバイアスがかけられています。このあまり知られていませんが、重大な問題はAccuracy Ratioと呼ばれる、予測値の実測値に対する比に基づいた指標を用いることで克服できます。このアプローチをとることでさらに優れた統計的手順を踏むことができ、幾何平均[1]の観点で解釈できる予測を導けます。
もう一つのMAPEの定義
実測値が小さい場合にMAPEを計算する場合は、問題が起こりえます。まれに起こる問題として、1を0で割ろうとすることがあります。また誤差が小さすぎる場合に、MAPEがとても大きくなるという問題もあります。
新たな選択肢として、実測値(公式では$A_t$)を全ての実測値の平均($\bar{A}_t$)に置き換えるという方法があります。この選択肢は、各地点の電気代[2]を予測するモデルのパフォーマンスの指標として使われています。
注意してほしいことは、これは絶対偏差の合計を実測値の合計で割ること同意であり、しばしばWAPE(加重絶対パーセント誤差)と呼ばれるということです。
問題点
MAPEが予測モデルの当てはまり具合を測る最も有名な指標の一つである一方で、この指標の欠点や、MAPEを使用することで紛らわしい結果が出てしまうことに対するさまざまな研究があります。[3][4]まず、MAPEは実測値が0($A_t=0$)の場合に使えないということです。加えて、MAPEはマイナスの誤差により重いペナルティーを与えてしまうことです($A_t<F_t$の場合)。[5]MAPEに関するこれらの問題を克服するために、別の指標を用いることもできます。以下に示します。
- 平均絶対スケール誤差(MASE)
- 対照的平均絶対パーセント誤差(sMAPE)
- MDA
- MAAPE(Mean Arctangent Absolute Percentage Error):MAAPEは新しい基準の絶対パーセント誤差であり、MAPEを異なる視点で研究することで開発されました。エッセンスとしては、MAPEが割合に傾斜をつけるものである一方、MAAPEは角度に傾斜をつけるものだといえます。[4]
関連リンク
絶対偏差の最小値
平均絶対誤差
平均パーセント誤差
対照的平均絶対パーセント誤差
外部リンク
回帰モデルにおける平均絶対誤差
平均絶対パーセント誤差
パーセント誤差における誤差
MAAPE
注釈
[1]Tofallis (2015). "A Better Measure of Relative Prediction Accuracy for Model Selection and Model Estimation", Journal of the Operational Research Society, 66(8),1352-1362. archived preprint
[2]Jorrit Vander Mynsbrugge (2010). "Bidding Strategies Using Price Based Unit Commitment in a Deregulated Power Market", K.U.Leuven
[3] Hyndman, Rob J., and Anne B. Koehler. "Another look at measures of forecast accuracy." International journal of forecasting 22.4 (2006): 679-688.
[4] Kim, Sungil and Heeyoung Kim (2016). "A new metric of absolute percentage error for intermittent demand forecasts." International Journal of Forecasting, volume 32 issue 3, pages 669-679.
[5] Makridakis, Spyros. "Accuracy measures: theoretical and practical concerns." International Journal of Forecasting 9.4 (1993): 527-529