Pythonで覗く, こわくない量子力学1 : 無限井戸型ポテンシャル

対象

量子力学を授業で習った or 自習した人に適した内容かと思います. 理系の学部生あたりでしょうか. プログラミングが好きだと尚良し！ 量子力学をまったく知らない人向けの内容ではありませんので悪しからず...

あらまし

量子力学の授業というと, 「おっかない計算を散々やらされた上に概念も理解できずに終わってしまった」という方も多いと思います. 御多分に洩れず自分もそのひとりでした.

量子力学には「概念の壁」と「数学の壁」の2つが存在する, と前野先生の本にはありました. その通りだと思います. 確かに量子力学の概念に慣れるのはなかなか骨の折れることです. 散々教科書を読みまくって, やっとなんとなく理解できてくるようなものだと思います. しかし, その過程で「数学の壁」が邪魔をしてきます. これが初学者にとっては大変に厄介で, 「数学」を越えようとしているうちに「概念」が頭から吹っ飛んでしまうことが多々あります. 逆に言えば, 「数学」と「概念」のどちらかのみであればめちゃくちゃ厄介ということは無いです¹. しかも, 量子力学における数学の基本は学部で習うような線形代数です.

ではその簡単な線形代数がいかにしてあのおぞましい計算に化けるのかといえば, 「Schroedinger方程式をがんばって解析的に解こうとしている」からです. でもこの計算は結局物理の本質ではありません. 大事なことは

1. 量子力学で扱う方程式は「定常Schroedinger方程式」と「時間依存Schroedinger方程式」²

2. 前者は「固有値方程式」, 後者は「線形微分方程式」であること

の2つです. 「固有値方程式」「線形微分方程式」であることがわかれば, それの解き方を覚える必要は(テストでもなければ)ありません. 「固有値方程式を解いた結果」を見て物理的な考察をする方が大切です. 物理が理解できればシナリオを掌握できれば, その過程である数学の理解も進むことでしょう.

この物理の理解にPythonの力を借りましょう. 「固有値方程式」「線形微分方程式」は形式に依らず, 数値計算ではそれぞれ同一のアルゴリズムで解くことができます. 「固有値方程式」はnumpy(scipy).linalg.eigh, 「線形微分方程式」はscipy.integrate.odeintやscipy.fftpack.fft, ifftなどを用います. 「この問題は解析的にどうやって解こうか...」なんて後回しにしましょう. まず数値計算で解いて, 物理的な考察をしてから考えることにしましょう.

「Pythonなんてわからん！」という方でも, C言語がそこそこ理解できれば大丈夫だと思います. Pythonにおける数値計算手法については

NumPyを用いた数値計算の高速化 : 基礎
NumPy・SciPyを用いた数値計算の高速化 : 応用その1
NumPy・SciPyを用いた数値計算の高速化 : 応用その2

などを見て頂けるとなんとなくニュアンスが掴めるかもしれません.

めざすところ

1. 解くべき方程式は何か
2. 数値計算で解いてみる
3. 値・グラフを見て考察
4. 解析解との比較

の順に話を進めます. 解析手法についてはそんなに深く立ち入りません. 教科書を参考にしてください. 量子力学なんて単なる線形代数³を標榜して進められればいいな思います.

無限井戸型ポテンシャル

一次元の空間に閉じ込められた粒子の持つエネルギーについて考えてみましょう. 解くべきは定常Schroedinger方程式であり, 固有値方程式です:

H\psi_\ell(x) = \left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + V(x)\right)\psi_\ell(x) = E_\ell\psi_\ell(x)\\
V(x) = \begin{cases}
0 & 0 < x < L\\
\infty & otherwise
\end{cases}

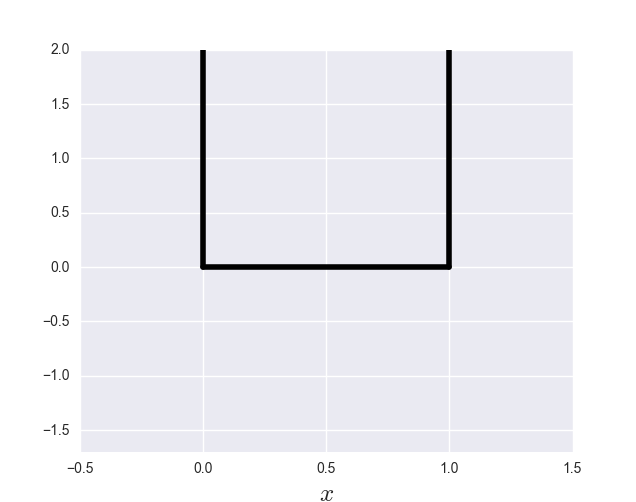
$x = 0, L$に無限に高い壁があるので粒子は$0 < x < L$にしか存在できないような系です. $0 < x < L$では自由粒子として振る舞います. ポテンシャルはこんなかんじですね:

何はさておき, これを数値計算で解いてみましょう.

差分化

(差分化の詳細はNumPy・SciPyを用いた数値計算の高速化 : 応用その1にあります)

系のサイズを$\left[0, L\right]$としましょう. それより外側には波動関数は存在できません. 系の差分化は

H\psi = (K + V)\psi = \frac12
\begin{pmatrix}
\frac{2}{\Delta q^2} + V(0)&\frac{-1}{\Delta q^2}&0&\cdots&0\\ 
\frac{-1}{\Delta q^2}&\frac{2}{\Delta q^2} + V(\Delta q) &\frac{-1}{\Delta q^2}&&0\\
0 & \frac{-1}{\Delta q^2}&\frac{2}{\Delta q^2} + V(2\Delta q)&& \vdots\\
\vdots&&&\ddots&\frac{-1}{\Delta q^2}\\
0& \cdots& 0 &\frac{-1}{\Delta q^2}& \frac{2}{\Delta q^2} + V(L)
\end{pmatrix}
\begin{pmatrix}
\psi_0\\
\psi_1\\
\vdots\\
\psi_{n-1}\\
\psi_n
\end{pmatrix} = E_\ell\psi

ですね. これをnumpy.linalg.eighに投げてあげることで固有値と固有関数を得ることができます.

実装

import numpy as np
from scipy.integrate import simps
import matplotlib.pyplot as plt
import seaborn

## set parameters
L, N = 1, 200
x, dx = np.linspace(0, L, N), L / N

## set kinetic matrix
K = np.eye(N, N)
K_sub = np.vstack((K[1:], np.array([0] * N)))
K = dx**-2 * (2 * K - K_sub - K_sub.T)

V = np.diag([0] * N)

## set Hamiltonian
H = (K + V) / 2

## solve igenvalue equation
w, v = np.linalg.eigh(H)

## plot
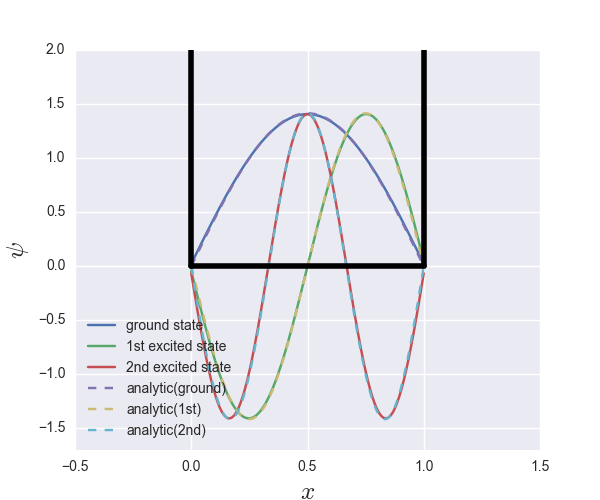
plt.plot(x, v.T[0] / simps(v.T[0]**2, x)**0.5, label="ground state")
plt.plot(x, v.T[1] / simps(v.T[1]**2, x)**0.5, label="1st excited state")
plt.plot(x, v.T[2] / simps(v.T[2]**2, x)**0.5, label="2nd excited state")
plt.plot(x, 2 * np.sin(np.pi * x /L) / np.sqrt(2 * L), '--', label="analytic(ground)")
plt.plot(x, -2 * np.sin(2 * np.pi * x /L) / np.sqrt(2 * L), '--', label="analytic(1st)")
plt.plot(x, -2 * np.sin(3 * np.pi * x /L) / np.sqrt(2 * L), '--', label="analytic(2nd)")
plt.show()

今後とも, 固有値方程式は上とほとんど変わらない方法で解いていきます. 系に依るのはポテンシャルくらいです. $m = \hbar = L = 1$という無次元化を施し, プロットの際に規格化しています.

エネルギー固有値も見てみましょう

n = np.arange(1, 11)
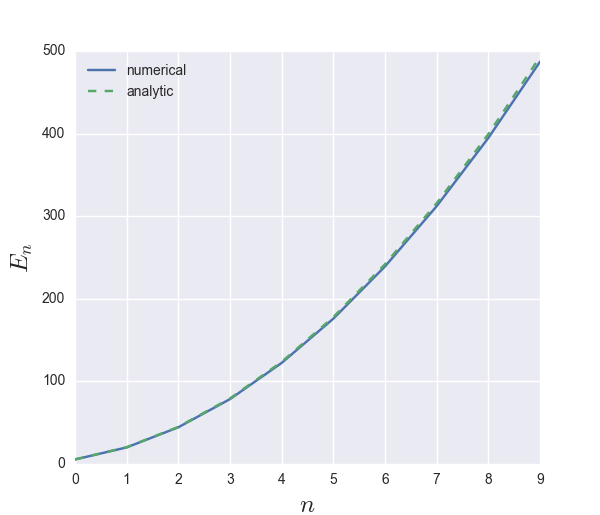
plt.plot(w[:10], label='numerical')
plt.plot(n**2 * np.pi**2 / (2 * L**2), '--', label='analytic')
plt.show()

曲線でつなげてしまいましたが, 横軸は量子数$n$なので離散的なグラフです. 繰り返しますが, 差分化してはいるものの, ハミルトニアンの固有値方程式を解いただけです. ただの線形代数ですね.

解釈

波動関数を「波動」だと思って, はじっこを固定(固定端)したときに許される波動関数やエネルギーはなんだろう？ということを計算したわけです. そして見事にエネルギーが不連続になりました. これが量子力学の特徴のひとつでしたね⁴. $\psi$を単なる粒子だと考えると(つまり古典力学)絶対に出てこない結論です.

解析解

波動関数と固有エネルギーの解析解は

\psi(x) = \sqrt{\frac{2}{L}}\sin\left(\frac{n\pi x}{L}\right), \hspace{1cm} E_n = \frac{n^2 \pi^2 \hbar^2}{2mL^2}

でした. 先のグラフに既に乗っけたのですが, 破線が解析解です. 非常によく一致していますね.

これを求めるためには$\psi(0) = \psi(L) = 0$という境界条件を設定して微分方程式を解きます. この境界条件のおかげで量子数$n$が出現し, 励起状態を考えることができるのです. ではなぜ固有値方程式だったものを微分方程式に置き換えて考えるのかといえば, 固有値方程式のままでは解析的に解くことが難しいからです⁵.

今後出てくる煩雑な計算の根源はだいたいこれだと思ってください. 固有値方程式のままでは解析的に解くことが難しいから微分方程式に置き換えるのです. そして難しい数学に豹変するのです.

しかし, 数値計算ではこの困難はありません. シンプルに固有値問題を解けばよいのです. それが本来の量子力学の姿なのです⁶. そう考えると気が楽になりませんか？

おわりに

量子力学における数学の壁は, なんとか解析的に問題を解こうとした先人たちの努力によるものです. ただ, その計算は公式集を見ながらで構わないのです. 「固有値方程式を解きたいだけなのに」ということを理解していれば, その数学が物理の本質ではないことがわかりますね. そして, 数学は数学として理解に努めればよいのです. かくして「概念の壁」と「数学の壁」が分離できるのです. めでたしですが, 次に続きます.

Pythonで覗く, こわくない量子力学2 : 有限井戸型ポテンシャル

1. 「量子力学は数学と概念がリンクして初めて理解することができるのだ！」と思う方もいらっしゃると思います. 僕もそうだとは思いますが, 双方を同時に理解することは難しいでしょう. ↩

2. 「Heisenberg方程式もあるじゃん」はスルーします. 等価なので. ↩

3. 怒る人も居そうですが, 大目に見て頂けるとうれしいです ↩

4. エネルギーが離散になるのは束縛状態のときであり, 連続になるようなものだってあります. 例えば一様系の自由粒子とか. ↩

5. 行列と演算子が異なる概念であるということが原因のひとつです. 固有値方程式がそのまま解けるのは調和振動子くらいなものです. ↩

6. 解析計算を軽んじている訳では決してありません. 解析計算(近似計算も含む)なくして数値計算に意味はありません. ↩