対象
Python及びNumPy初心者に向けて書いています. 「C言語は使えるけど最近Pythonを始めた」とか「Pythonらしい書き方がよくわからない」に該当する物理系の数値計算を目的とした方には特に有用かもしれません.
また, 自分の不勉強のために間違った記述があるかもしれません. ご容赦ください.
あらまし
NumPyを用いた数値計算の高速化 : 基礎
NumPy・SciPyを用いた数値計算の高速化 : 応用その1
の続きになります. 基礎的な数値計算の手法を追っていきますが, 今回は少し発展的な内容も含みます.
代数方程式 / 超越方程式
代数方程式はいわゆる手で解けるふつうの方程式です. 超越方程式は随分大仰な名前ですが, 代数的な手法で解けない方程式のことを指します. 具体的には
$$
\sin(x) = \frac{x}{2}
$$
こんな子です. この方程式は, 「$\sin(x)$を知るためには$\frac{x}{2}$が必要で, $\frac{x}{2}$を知るには$\sin(x)$が必要」という構造を持っているため, 「自己無撞着(self-consistent)方程式」とも呼ばれます. 代数的に解けなくても数値的に解くことはもちろん可能です. アルゴリズムは「Newton法」や「二分法」が挙げられます. アルゴリズムの詳細は省略しますが, そんなに難しくないので知らない方は調べてみてください. これらの実装は単純ですが, 結局は逐次代入をしているようなものなのでforループの使用が避けられません. Newton法だと基本的に収束は速いのですが, 微分可能な関数であることが条件で, 性質の良い関数が要求されます. 一方で2分法は指定した区間に解があれば必ず見つけることができますが, 収束までの反復回数は多くなります.
ただ, もうお気づきかもしれませんが, これらはscipy.optimizeというモジュールに既に実装してあります. forループ云々は関数の中で完結しており, 高速に動作してくれます.
実装
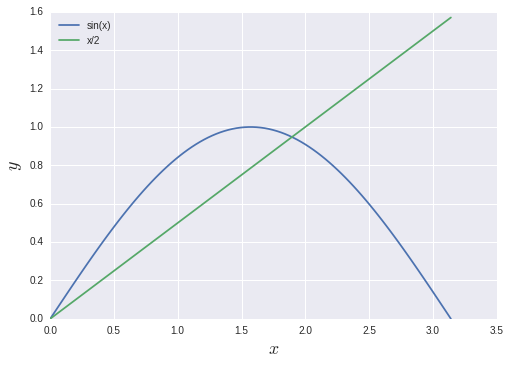
上の方程式の解がだいたいどこにあるのかを確認します:
だいたい$x \in (1.5, 2.0)$にあることがわかりますね. これを二分法で解いてあげます:
from scipy.optimize import bisect
def f(x):
return np.sin(x) - x/2
bisect(f, 1.5, 2)
>>> 1.895494267034337
非常にシンプルです. 区間内に解が2つ以上あるとどちらに収束するかわからないので, 必ず1つになるようにしましょう. もちろん代数的方程式でも使えます.
Fourier変換
Fourier変換と言えば信号処理などでおなじみですが, 今回も物理の話で進めさせて頂きます. 少し数学的な話が多くなりますがご了承ください. 前の記事で扱った拡散方程式を思い出してください:
$$
\frac{\partial}{\partial t}f(x, t) = \frac{\partial^2}{\partial x^2}f(x, t)
$$
この子はFourier変換で解いてあげることができるのでした. その方法を見ていきましょう. Fourier変換と逆Fourier変換を以下のように定義します:
\tilde{f}(k, t) = \frac{1}{\sqrt{2\pi}}\int dx e^{-ikx}f(k, t) = {\cal F}[f(x, t)]\\
f(x, t) = \frac{1}{\sqrt{2\pi}}\int dk e^{ikx}\tilde{f}(k, t) = {\cal F}^{-1}[\tilde{f}(k, t)]
この定義を拡散方程式に代入してみましょう. すると, $x$微分が実行できてしまいます:
\frac{\partial}{\partial t}\left(\frac{1}{\sqrt{2\pi}}\int dk e^{ikx}\tilde{f}(k, t)\right) = \frac{\partial^2}{\partial x^2}\left(\frac{1}{\sqrt{2\pi}}\int dk e^{ikx}\tilde{f}(k, t)\right)\\
\frac{\partial}{\partial t}\left(\frac{1}{\sqrt{2\pi}}\int dk e^{ikx}\tilde{f}(k, t)\right) = -\left(\frac{1}{\sqrt{2\pi}}\int dk k^2e^{ikx}\tilde{f}(k, t)\right)\\
さらに$k$積分を外すと単なる$t$に関する1階微分方程式になっているので, 簡単に解いてあげることができます:
\frac{\partial}{\partial t}\tilde{f}(k, t) = -k^2\tilde{f}(k, t)\\
\tilde{f}(k, t) = e^{-k^2 t}\tilde{f}(k, 0)
そしてこれを逆Fourier変換してあげます:
\frac{1}{\sqrt{2\pi}}\int dk e^{ikx}\tilde{f}(k, t) = \frac{1}{\sqrt{2\pi}}\int dk e^{ikx}e^{-k^2 t}\tilde{f}(k, 0)\\
f(x, t) = \frac{1}{\sqrt{2\pi}}\int dk e^{ikx}e^{-k^2 t}\tilde{f}(k, 0)
$\tilde{f}$のままだとよくわからないので, $f$に直してあげます:
$$
f(x, t) = \frac{1}{2\pi}\int dk e^{ikx}e^{-k^2 t}\int dx' e^{-ikx'}f(x', 0)
$$
もし初期条件$f(x, 0)$の式がわかっており, かつそれが解析的に積分できるものであれば1解析解が求まります. もし解析的に積分不可能であればやはり数値的に解くありません.
さて, この流れをシンプルに書くと以下のようになります:
$$
f(x, t) = {\cal F}^{-1}[e^{-k^2 t}{\cal F}[f(x, 0)]]
$$
$f(x, 0)$をFourier変換した後, $e^{-k^2 t}$を掛けて逆Fourier変換すればよいのです. これの素晴らしいところは, $x$や$t$を差分化していないところです. 以前のような差分化を用いた方法だと, 微分を差分に置き換えることが基本なので, 差分の幅が小さいことが絶対条件でした. しかし, 今回ははじめに$x$や$f(x)$を差分化するものの, $\Delta x$のオーダーが計算結果に効いてくることはありません. $t$はそもそも差分化していません. つまり, $t$の時間をどんどん進めていっても誤差が蓄積しません. これはけっこう凄いことです.
さて, 最後に問題になるのが, $k$とはなにかということです. ある$N$個に差分化された$x_i$に対して$k_i$がどんな値を取るのでしょうか?これは$x_i$の離散Fourier変換について真面目に考えればわかりますが,
k_i =
\begin{cases}
2\pi\frac{i}{N}\hspace{0.5cm} (0 \le i < N/2)\\
2\pi\frac{N-i}{N}\hspace{0.5cm} (N/2 \le i < N)
\end{cases}
となっています. これは少しややこしいですね. しかし, SciPyはこの$k_i$を生成する関数まで用意しています. なんとも周到ですね.
実装
長々とお話してしまいましたが, コーディングはシンプルです. Fourier変換はscipy.fftpackに用意されています.
注意点は2点あります.
-
離散Fourier変換の仕様上, 分割数は2の累乗が好ましいです.
-
fftを噛ませて$k$空間に移るとcomplex型を経由するので,ifftをかけて$x$空間に戻しても虚部のゴミが残ってしまいます.realだけを取るかabsを取るようにしましょう.
from scipy.fftpack import fft, ifft, fftfreq
def f(x):
return np.exp(-x**2)
# set system
N, L = 256, 40.0
x = np.linspace(-L/2, L/2, N)
# set initial function
gaussian = f(x)
plt.plot(x, gaussian, label="t=0")
# set k_i
k = 2 * np.pi * fftfreq(N, d=1/N)/L
time = [2, 4, 8]
for t in time:
expK = np.exp(-k**2 * t)
result = ifft(fft(gaussian) * expK)
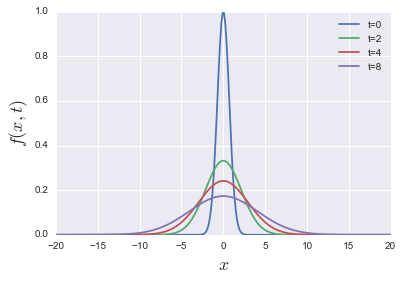
for文がありますがそこはご愛嬌...こういう時間ステップはしょうがないです. 今回は3回しか回してないですし. ただ, 注意したいのは2s→4s→8sのように逐次時間を進めているのではなく, それぞれ独立に時間発展を計算しているということです. つまり, 8sのグラフが欲しければ, t=8を代入するだけで良いのです. ここが差分法との最大の違いです.
前回と同じグラフが得られましたね. この方法は非常に強力でポテンシャルがある場合などにも応用でき, トロッター分解を用いたSymplectic法などに発展していきます...が, 専門的過ぎるのでここまでにしておきましょう.
非線形微分方程式(発展)
この内容はちょっと専門的です. 興味がなければスルーして頂いて結構ですが, 少し大事な話も含みます.
物理ではしばしば非線形微分方程式が出てきます. そんなある非線形方程式2
$$
\left(-\frac{1}{2}\frac{d^2}{dx^2} + g|\psi(x)|\right)\psi(x) = \mu\psi(x)
$$
があったとします. これは今までの方法で解くことは難しそうです. なぜなら差分化したときに行列の中に$\psi(x)$を含むからです. 具体的には
\left[
\frac{1}{2\Delta x^2}
\begin{pmatrix}
-2&1&0&\cdots&0\\
1&-2 &1&&0\\
0 & 1&-2&& \vdots\\
\vdots&&&\ddots&1\\
0& \cdots& 0 &1& -2
\end{pmatrix}
+g
\begin{pmatrix}
|\psi_0|^2&0&0&\cdots&0\\
0&|\psi_1|^2 &0&&0\\
0 & 0&|\psi_2|^2&& \vdots\\
\vdots&&&\ddots&0\\
0& \cdots& 0 &0& |\psi_n|^2
\end{pmatrix}
\right]
\begin{pmatrix}
\psi_0\\
\psi_1\\
\vdots\\
\psi_{n-1}\\
\psi_n
\end{pmatrix}
= T(\psi)\psi
=\mu\psi
これは$T\psi$のような線形作用素で書くことができないということであり, これが「非線形」ということばのひとつの解釈です. 上では無理やり行列で書いていますが, $T(\psi)\psi$になってしまいます. $\psi$を求めたいのに, それを求めるために必要な行列が$\psi$を含んでいるという構造ですね. これを自己無撞着的と呼ぶのでした.
さて, ここで上の微分方程式を$\mu$を固有値とした固有値方程式と見立ててあげます:
$$
T(\psi)\psi = \mu_n \psi
$$
自己無撞着方程式であることから以下のようなアイデアが浮かびます:
-
この非線形微分方程式を満たす特解の形がある程度わかっていたとき, その解に近い$\psi$を使って$T(\psi)$をつくり, 固有値方程式を解く.
-
得られた固有ベクトルの中で, 今求めようとしているものに一番近いものを選ぶ.
-
その固有ベクトルで再び$T(\psi)$をつくり固有値方程式を解く...ということを繰り返した結果, $\psi$の形が変わらなくなったときにこれは元の微分方程式の解になっており, そのときの$\mu$の値も同時に決定される.
そして, 上の非線形方程式にはソリトン解が存在し, その中でも$g < 0$のときにはブライトソリトンと呼ばれるガウシアンに似た3特解が存在します. というわけで, $\psi$の初期関数にガウシアンを選んでこのアイデアを実装してみましょう.
実装
def h(x):
return x * np.exp(-x**2)
# set system
L, N, g = 30, 200, -5
x, dx = np.linspace(-L/2, L/2, N), L / N
# set K matrix
K = np.eye(N, N)
K_sub = np.vstack((K[1:], np.array([0] * N)))
K = (dx**-2 * (2 * K - K_sub - K_sub.T)) * 0.5
# set initial parameter
v, w, mu = np.array([h(x)]).reshape(N, 1), np.array([3]), 0
# self-consistent loop
while abs(w[np.argmin(w)] - mu) > 1e-5:
# update mu
mu = w[np.argmin(w)]
# set G matrix
G = g * np.diag(np.abs(v.T[np.argmin(w)])**2)
# solve
T = K + G
w, v = np.linalg.eigh(T)
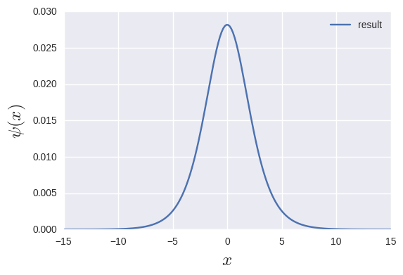
今回は繰り返す関数に$v.T[0]$を選びました. 今回の微分方程式では一番低いエネルギー固有関数に1ソリトンが対応しているようです4. 収束条件は$\mu$に課しています. このぐらいの制度で, 16回ほどループしていました. これをプロットしてみましょう:
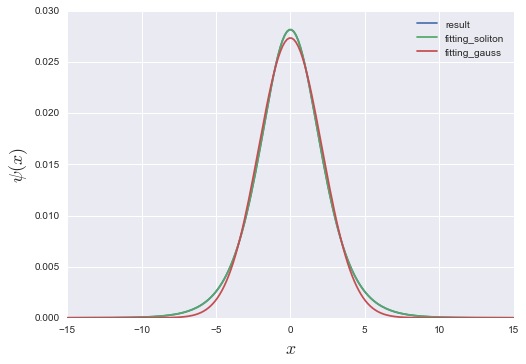
ソリトンっぽいですが, ガウシアンでないかが不安です. 試しにソリトンの一般解
f_s(x) = \frac{b}{a\cosh(x)}
とガウシアンでフィッティングしてみましょう:
from scipy.optimize import curve_fit
def bright_soliton(x, a, b):
return (b / np.cosh(a * x))**2
def gauss_function(x, a, b):
return a * np.exp(-b * x**2)
param_soliton = curve_fit(bright_soliton, x, v.T[0]**2)[0]
param_gauss = curve_fit(gauss_function, x, result)[0]
resultとbright_solitonはぴったり一致しました. ガウシアンとはフィットしなかったので, 恐らくソリトンで間違いないでしょう.
ちょっと小難しい話が続きましたが, 今回重要なのはソリトン云々ではなく, 自己無撞着方程式のような値を変えつつ行列を初期化して計算を繰り返すようなコードにおいては, いちいち初期化にループを用いていると大変な時間がかかるだろうということです. 自己無撞着ループ + 行列の初期化2ループ = 3ループみたいなことをやっているともうたいへんです. こういうアルゴリズムをPythonで相手にするにはNumPyが不可欠なのです. 以前の基礎編で書いた「巨大な行列をパラメータを変えるごとに都度初期化して計算を進めるようなタスクでは, 大きな威力を発揮します」とは今回のような計算を指すのでした.
さいごに / 個人的なこと
基礎的な数値計算の実装についてお話ししてきました. これ以上はやや専門的になるかと思うのでここまでとします. あとは自分がやりたい計算に合わせてNumPy・SciPyのリファレンスを見ていただけると良いかと思います. とは言いつつも, 少し語り残したこともあるのでまた別記事にまとめるかもしれません.
そもそもこの記事を書こうと思った動機は, この手の高速化に関する情報があまりネット上に無いなあと感じていたからです. 自分は以下のような道を辿ってきました.
-
Pythonのシンプルな仕様と数値計算のライブラリの豊富さに感動. 自分の研究にも使いたいが, C++のコードをそのまま落とし込むと非常に遅い. ハードな数値計算に対応できないのだろうか?と模索を始める.
-
「NumPyが高速だ!」という話は至るところでされていますが, Cから移行してきた人は結局for/while文を使ってしまいます. NumPy配列をfor文に渡すという愚行を犯し, 「ぜんぜん早くないじゃないか!」と思っていました. 今考えると滑稽ですね.
-
「for文が遅い!」という話もまた各方面でされていますが, Cから移行してきた人はfor/while文を使わずにどうやって数値計算のコードを書けばよいのかがわからないのです. 確かに行列演算は高速なのでしょうが, その行列をどうやって用意するか, 行列以外の計算はどうなのか等々悩みが尽きませんでした.
-
「リスト内包は普通のfor文より速い!」とも言われますが, 正直微々たる差でした.
-
そして行き着く先がCython, Boost/Python, Numbaなど5でした. これらのツールは確かに高速にはなるものの制約が多く, どんどんCライクなコードに豹変していきます.
-
結果「C++でよくない?」となるわけです. しかしPythonに慣れた身ではC++の難解な言語仕様に嫌気が差してしまいます.
-
5.に戻る
...ということを1年近く繰り返していました. NumPyのマニュアルを読めばそれぞれの関数の使い方はわかりますが, for文を使わないことを明示的に徹底した数値アルゴリズムの解説はあまり見当たらなかったように思います. **「極力for文を使わないで!NumPyのユニバーサル関数を使って!お手本見せるから!」**という具合の情報が自分の前に転がっていればこんなに回り道することも無かったかと思います.
こういう経緯から, 基礎的な数値計算アルゴリズムのクックブック的なものを目指して書いたつもりです. 数値計算の実行速度に悩む方々の助けになれば幸いです.